Entwicklung des SATOR-Quadrats in vier
Achsenkreuzen und Quadraten
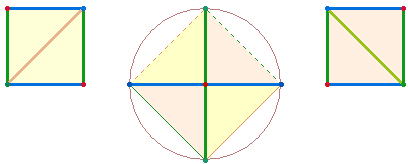
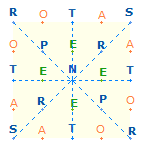
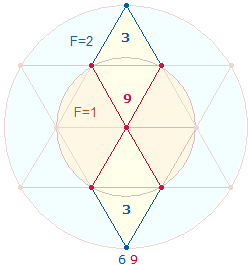
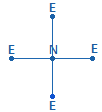
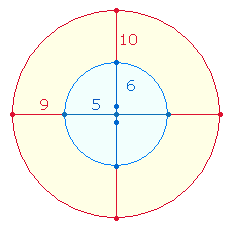
1. Jeder Organismus hat einen Anfang und entwickelt sich in Bausteinen. Dies gilt auch für das Dezimalsystem und für systemrelevante geometrische Figuren. Die grundlegende geometrische Figur ist der Kreis. Durchmessergeraden führen zu Unterteilungen, die Maß und Zahl begründen. Ein rechtwinkliges Achsenkreuz wird durch Winkelverschiebung zu einem Quadrat:
|
|
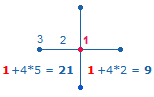
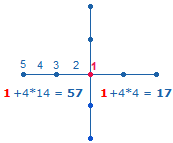
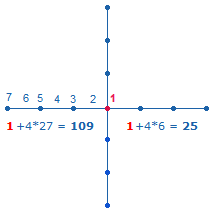
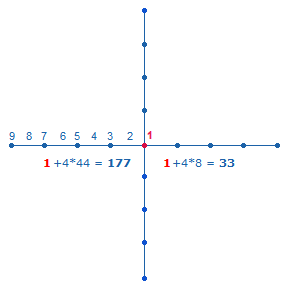
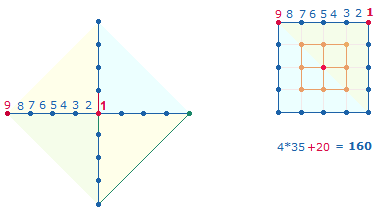
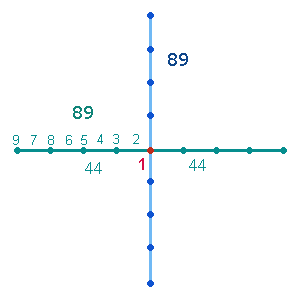
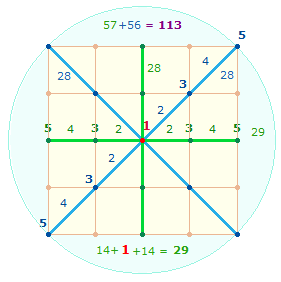
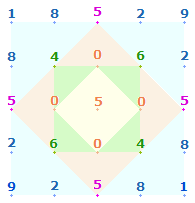
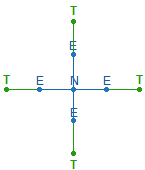
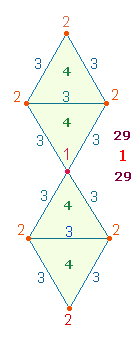
1. Jedes Achsenkreuz hat 4 Achsenarme, deren niedrigste Ausdehnung aus einer Maßeinheit (Linie) und einem Punkt, also aus 2 Elementen, besteht. Ein Achsenkreuz kann um jeweils 8 Elemente erweitert werden. Das vierte Achsenkreuz in Folge ist die Grundlage des SQ, da es entsprechend den beiden konzentrischen Tetraktyskreisen aus zwei konzentrischen Quadraten besteht. Die Elemente jedes Achsenkreuzes können einfach und numeriert gezählt werden. Jede Numerierung beginnt vom Mittelpunkt aus:
|
|
|
|
|
Die Zahl der Punkte je Achsenarm gibt die Bezeichnungen der Achsenkreuze von AK2 – AK5 an. Es ergeben sich folgende numerierte und unnumerierte Summen:
|
|
AK2 |
AK3 |
sm |
AK4 |
AK5 |
|
|
num. |
21 |
57 |
78 |
109 |
177 |
364 |
|
unnum. |
9 |
17 |
26 |
25 |
33 |
84 |
|
|
30 |
74 |
104 |
134 |
210 |
448 |
|
364:84 = 28*(13:3) = 28*16 |
||||||
|
240:208 = 16*(15:13); 26:78 = 26*(1:3) |
||||||
|
78:286
= 26*(3:11) = 26*14 |
||||||
364 = 2*182 ist bemerkenswert, weil es die Zahlensumme (ZS) von zweimal SATOR OPERA TENET ist. Die Summe 364 kommt durch folgende Numerierungssummen zustande, ausgehend von einem Achsenarm: 6+15+28+45 = 94; 94-4 = 90; 4*90 = 360; 360+4 = 364 = 4*91.
Es fällt weiterhin auf, daß 21+57 = 78 die Faktorensumme (FS) von IUPPITER mit der ZS 109 ist:
|
|
I |
U |
I |
sm |
P |
P |
T |
E |
R |
sm |
|
|
ZW |
9 |
20 |
9 |
38 |
15 |
15 |
19 |
5 |
17 |
71 |
109 |
|
FW |
6 |
9 |
6 |
21 |
8 |
8 |
19 |
5 |
17 |
57 |
78 |
|
|
|
|
|
59 |
|
|
|
|
|
128 |
187 |
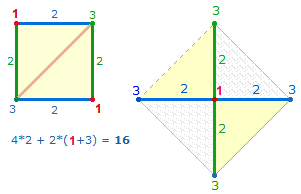
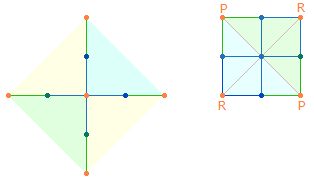
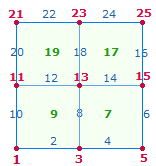
2. Die Numerierung der Achsenkreuze läßt sich auf die 4 Quadratseiten übertragen. Dabei verdoppelt sich die 1 des Mittelpunktes, während vier deckungsgleiche Endzahlen nur zweimal gerechnet werden:
|
|
|
|
|
|
Aus praktischen Gründen sollen die Quadrate dieselbe Nummernbezeichnung erhalten wie die Achsenkreuze: Dabei wird die Zahl der Punkte je Achsenarm auf die ganze Quadratachse sowie auf die Seiten des Quadratrahmens ausgedehnt.
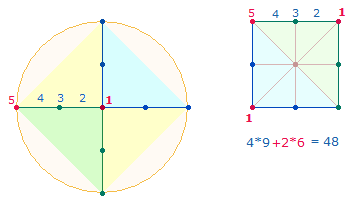
Die Summen der vier Quadratrahmen können nach Binnen- und Eckzahlen aufgeteilt werden:
|
|
1-3 |
1-5 |
1-7 |
sm |
1-9 |
GS |
|
Bi.Z |
8 |
36 |
80 |
124 |
140 |
264 |
|
Eck.Z |
8 |
12 |
16 |
36 |
20 |
56 |
|
sm |
16 |
48 |
96 |
160 |
160 |
320 |
|
16:48:96 = 16*(1:3:6) = 16*10 |
||||||
|
264:56 = 8*(33:7) |
||||||
Die Summen der ersten drei Quadrate sind gleich der Summe des vierten Quadrats, woraus sich das Verhältnis 3:1 ergibt. Die Verhältniszahlen 1:3:6 geben die Punktestruktur der Tetraktys wieder:
|
|
2*160 ist also auf 2*10 Punkte der beiden Tetraktys beziehbar, auf einen Punkt entfällt die Zahl 16. 136 ist die Summe der Zahlen von 1-16.
Ohne Numerierung ist die Summe der Binnenzahlen 4*(1+3+5+7) = 4*16 = 64 und der Eckzahlen 4*4 = 16, zusammen 80. Die durchschnittliche Numerierungszahl der Numerierungssumme 320 ist daher 4.
Die 4 Achsenkreuze bilden eine inhaltliche Ganzheit der Grundzahlen von 1-9. Dementsprechend sind die Verhältniszahlen 33 und 7 aus Komplementärzahlen von 2*20 zusammengesetzt: 1+2 = 3; 9+8 = 17; 1+3 = 4; 9+7 = 16. 182+155 = 337 ist die ZS+FS von SATOR OPERA TENET.
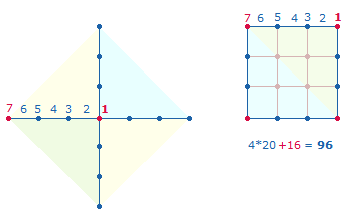
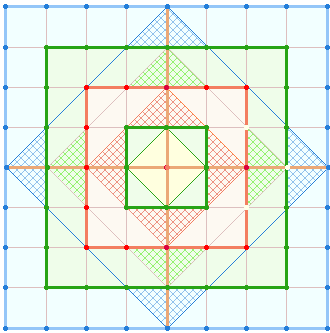
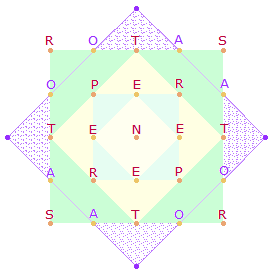
3. Die aus den Achsenkreuzen hervorgegangenen Quadratrahmen enthalten – außer dem ersten – Punkte, die horizontal und vertikal verbunden werden können und somit weitere Schnittpunkte und Einzelquadrate hervorbringen. Das erste (1-3) und dritte Quadrat (1-7) hat eine quadratische Fläche statt eines Punktes zur Symmetriemitte. Flächen, Punkte und Flächen+Punkte+Linien schreiten in quadratischen Zahlen voran, die Zahl der Linien ist jeweils 1 weniger als Flächen und Punkte zusammen:
|
|
F |
P |
L |
FPL |
F+P+FPL |
|
|
1-3 |
1 |
4 |
4 |
9 |
1²+2²+3² |
14 |
|
1-5 |
4 |
9 |
12 |
25 |
2²+3²+5² |
38 |
|
1-7 |
9 |
16 |
24 |
49 |
3²+4²+7² |
74 |
|
1-9 |
16 |
25 |
40 |
81 |
4²+5²+9² |
122 |
|
|
30 |
54 |
80 |
164 |
|
248 |
|
30+54 =
84; 84:80
= 4*(21:20) = 4*41; 248 = 8*31 |
||||||
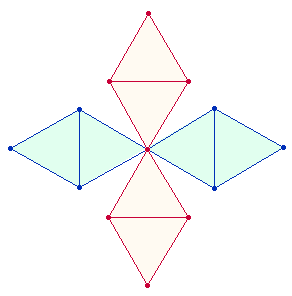
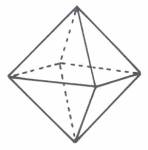
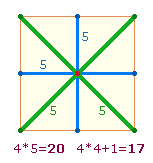
Aus 21+20 = 41 Elementen besteht ein Doppelrautenkreuz, das zu einem Oktaeder zusammengesetzt werden kann:
|
|
|
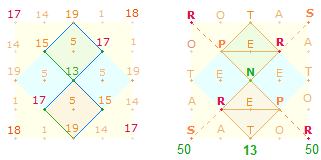
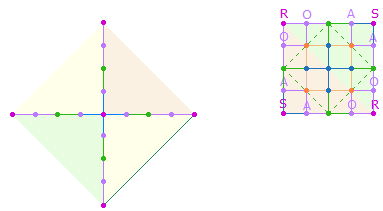
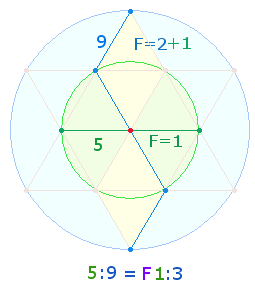
4. Um konzentrische Quadrate fortlaufend in Kreisform zu numerieren, kommen nur Punkte in Frage. Konzentrische Quadrate schreiten in ungeraden Zahlen ab 3 voran. Jedes Quadrat ist nach der Zahl der Punkte je Achse benannt, wie jedes Achsenkreuz nach der Punktezahl eines Achsenarmes (s.o.). Das Quadrat Qu3 ist das erste mit Diagonalachsen, das Qu5 die erste Erweiterung um 8 Punkte. Jeder weitere Quadratrahmen wächst um 8 Punkte. Achsenkreuze und Quadrate mit Mittelpunkt schreiten in ungeraden Zahlen (3, 5, 7, 9 usw.) voran, Achsenkreuze und Quadrate mit quadratischer Mitte in ungeraden Zahlen (2, 4, 6, 8 usw.).
Zwischen dem AK4 und dem Qu5 besteht eine besondere Beziehung: Das AK4 als Erweiterung der 17 Elemente des AK3 um 8 Elemente besteht aus 13 Punkten und 12 Linien. Die Einzelziffern von 13 und 12 sind Kreisflächeneinheiten der beiden konzentrischen Tetraktyskreise. Aus 13 Punkten und 12 Linien des AK4 werden im Qu5 13 ungerade und 12 gerade Punkte (8 orange + 4 grün; s.Grafik). Aus 17 Punkten bestehen die vier Achsen und die restlichen 8 geraden Punkte sind Binnenerweiterungen aus Qu3:
|
|
17+8 Punkte sind deshalb von so großer Bedeutung, weil sich die 25 Buchstaben des SQ aus 8 verschiedenen Buchstaben zusammensetzen und die ZS der 8:17 Buchstaben die Umkehrzahlen 102:201 sind. 178 selbst ist die Summe aus zwei numerierten Achsen von 1-9, wie oben schon gezeigt wurde, allerdings mit Zählung eines statt zweier Mittelpunkte:
|
|
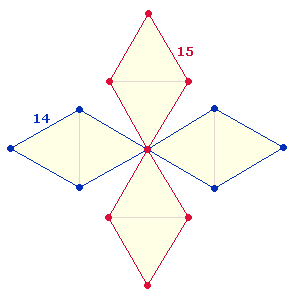
5. Verbindet man die vier äußeren Punkte eines rechtwinkligen Achsenkreuzes aus gleichlangen Achsenarmen, erhält man ein Rautenquadrat, das halb so groß wie das Quadrat, dessen Seitenlängen aus parallelen Schnittpunkten der beiden Achsen zustande kommen. Das Rautenquadrat unterteilt das horizontal-vertikale Quadrat in zweimal vier spiegelsymmetrische rechtwinklige Dreiecke:
|
|
Dieses Muster aus zwei Quadraten
wiederholt sich bei linear wachsenden Achsenkreuzen. Die beiden
Ausgangsquadrate bestehen aus 5 und 9 Punkten. Die Zahl der Punkte vergrößert sich mit
jedem größerem Doppelquadrat nach einem
bestimmten Muster:
|
|
Bei der Erweiterung eines Achsenkreuzes
bilden 4 Außenpunkte der Achsenarme eine unveränderliche Konstante
für Rautenquadrate und normale Quadrate:
|
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
|
RQ3 |
RQ5 |
RQ7 |
RQ9 |
|
Qu3 |
Qu5 |
Qu7 |
Qu9 |
|
P |
1 |
5 |
13 |
25 |
|
1 |
9 |
25 |
49 |
|
+ |
4 |
4+4*1 |
4+4*2 |
4+4*3 |
|
4+4*1 |
4+4*3 |
4+4*5 |
4+4*7 |
|
|
5 |
13 |
25 |
41 |
|
9 |
25 |
49 |
81 |
Die 25 Punkte des SQ
enthalten ein inneres Quadrat aus 9 Punkten und 5+13 Punkte zweier Rautenquadrate. Es
kommen somit 18+34 = 2*(9:17) oder 27+25 = 52
= 4*13 Punkte zustande.
Der lineare Zuwachs an Punkten der ersten
beiden Rautenquadrate und normalen Quadrate beträgt:
|
|
RQ3 |
Qu3 |
RQ5 |
Qu5 |
|
|
5 |
9 |
13 |
25 |
|
+ |
0 |
4 |
4 |
12 |
Die Aufaddierung zeigt folgende
Vielfache des inneren Rautenquadrats und der nächsten drei Erweiterungen:
|
|
RQ3 |
Q3 |
RQ5 |
Qu5 |
|
|
x |
4 |
3 |
2 |
1 |
|
|
P |
5 |
4 |
4 |
12 |
25 |
|
sm |
20 |
12 |
8 |
12 |
52 |
Die entsprechenden ZS+FS des SQ
und ihre Vielfache sind folgende:
|
|
RQ3 |
Q3 |
RQ5 |
Qu5 |
|
|
ZS |
33 |
64 |
76 |
130 |
303 |
|
FS |
33 |
50 |
76 |
90 |
249 |
|
x |
4 |
3 |
2 |
1 |
|
|
sm |
132 |
192 |
152 |
130 |
606 |
|
sm |
132 |
150 |
152 |
90 |
524 |
|
|
264 |
342 |
304 |
220 |
1130 |
|
264:220 = 44*(6:5); 342:304 = 38*(9:8) |
|||||
|
524 = 4*131 |
|||||
Die Aufaddierung der ZS der 52
Buchstaben führt zu folgendem Ergebnis:
|
|
RQ3 |
Q3 |
RQ5 |
sm |
Qu5 |
GS |
|
P |
5 |
9 |
13 |
27 |
25 |
52 |
|
|
33 |
97 |
173 |
303 |
303 |
606 |
|
|
130 |
173 |
|
|
|
|
Die ZS 303 von 27 aufaddierten Buchstaben ist gleich der ZS der
nicht auffaddierten 25 Buchstaben. Die ZS der 14 Buchstaben der ersten beiden Quadrate beträgt
ebenso 130 wie die der 4*3
Eckbuchstaben des äußeren Quadratrahmens.
6. Die Zahl 113 nimmt in den Zahlenwerten des SQ ein bedeutende Stellung ein: Sie ist zunächst die FS der Diagonalachsen: RS = 25; PR = 25; 4*25+13 = 100+13 = 113.
|
|
Die ZS+FS der Diagonalachsen beträgt 147+113 = 260, die ZS+FS von viermal TE des
horizontal-vertikalen Achsenkreuzes 4*(24+24) = 192, zusammen 260+192
= 452 = 4*113, also 113
je Achse.
Die Bedeutung der Zahl 113 liegt darin,
daß sie die Numerierungssumme von vier Achsen mit je 5
Elementen je Achsenarm ist:
|
|
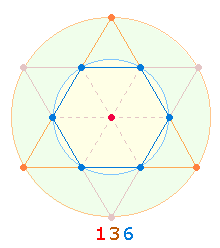
Die
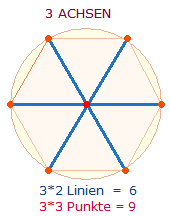
Umkehrzahlen 113+131+311 = 555 sind Primzahlen. Ihre Einzelziffern bilden 6 Maßeinheiten und 9 Punkte
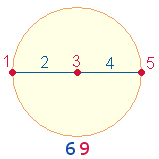
der drei Hexagonachsen. Auch eine numerierte Einzelachse ergibt 6+9:
|
|
|
Die Konstitutivzahlen der Zahlen 113 und 131 sind 56+57,
65+66 und deren Faktorenwerte
(FW) 13+22 = 35 und 18+16 = 34, zusammen 69, die ZS von SATOR. 35 ist die ZS von RS, 34 der Mittelbuchstaben OTA.
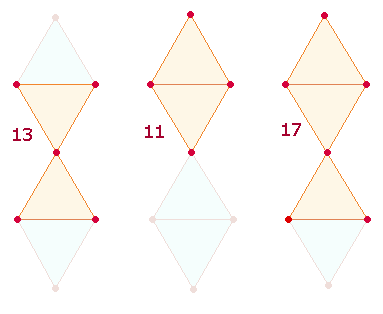
Die Summen 35 und 34
können an den drei Figuren der Doppelraute (DR) erkannt
werden:
|
|
Das sanduhrförmige Doppeldreieck des
Hexagons erweitert sich nach oben und unten durch jeweils eine Raute, woraus
sich 11+13+11 = 35 ergibt, während zwei
"Fischfiguren" von den äußeren Punkten der DR jeweils aus 17 Elementen bestehen. 6+9 kann sich
daher auch auf die Rahmenelemente der DR beziehen,
deren (nicht-numerierte) Erweiterungselemente 6
und deren hexagonale Elemente 9 sind:
|
|
7. Die Aufrechnung zweier Quadratpaare des 5x5-Punktequadrats läßt sich auch auf die 1x1 Vorlage des SQ anwenden:
|
|
|
|
RQ3 |
Q3 |
RQ5 |
sm |
Qu5 |
GS |
|
P |
5 |
9 |
13 |
27 |
25 |
52 |
|
ZS |
5 |
25 |
45 |
75 |
105 |
180 |
|
FS |
5 |
23 |
43 |
71 |
89 |
160 |
|
sm |
10 |
48 |
88 |
146 |
194 |
340 |
|
75:105 = 15*(5:7) |
||||||
|
160:180 = 20*(8:9) |
||||||
|
160:180 = 20*(8:9) = 20*17 |
||||||
Die Produktzahlen 20*17 lassen sich auf die Elemente von
vier Achsen eines Quadrats Qu3 beziehen:
|
|
Jede Achse besteht aus 3 Punkten + 2 Maßeinheiten.
Bei Einfachzählung des Mittelpunktes reduzieren sich die 20 Elemente auf 17.
Das Verhältnis 75:105 = 15*(5:7) weist auf 15
Rahmenelemente der DR hin und auf das Verhältnis von 5:7 Punkten der
DR in der Bedeutung
von 1:3 Kreisflächeneinheiten.
8. In einem weiteren Anlauf ist das Verhältnis von Achsenkreuzen, Rautenquadraten und regulären Quadraten, die für das SQ relevant sind, zu klären. Es ist noch einmal das Ausgangsachsenkreuz zu betrachten:
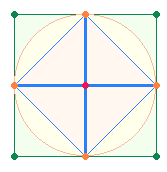
Zu überlegen ist, wie das rechte erweiterte Quadrat entsteht. Die folgenden
beiden Möglichkeiten sollen nicht weiter verfolgt werden:
· Vier
rechteckige Dreiecke des Rautenquadrats können spiegelsymmetrisch nach außen
geklappt werden.
· Die
Winkelverschiebung kann nach vier Richtungen erfolgen, um so ein
horizontal-vertikales Quadrat zu erstellen.
Wenn diese beiden Möglichkeiten
unberücksichtigt bleiben sollen, sind zur Quadratbildung nur entsprechende
Achsenkreuze zu betrachten. Dabei ist zu bedenken, daß ein Rautenquadrat durch
Winkelverschiebung eine kleinere Fläche und Ausdehnung besitzt, daß also das
Rautenquadrat dem regulären Quadrat immer vorausgeht.
Für das SQ
kommen die drei Achsenkreuze AK2, AK3 und AK5 in Frage:
|
|
Das AK3
hat eine doppelte Funktion, einmal als Rautenquadrat unter Hinzufügung von 4 Achsenkreuzpunkten und einmal durch Umwandlung
in ein reguläres Quadrat mit 4 Eckpunkten:
|
|
|
Das AK4
durchquert als Rautenquadrat die – noch
nicht vorhandenen – 8 Punkte neben den 4
Eckpunkten:
|
|
Durch das AK5 und Qu5 werden den
bisherigen 13 Buchstaben 12 hinzugefügt:
|
|
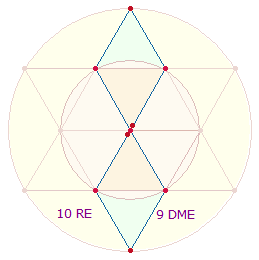
9. Wie dargelegt, baut sich das TENET-Kreuz (TK) aus AK2 und AK3 auf, der innere und äußere Quadratrahmen des SQ aus den verschobenen Winkeln von AK3 und AK5. Das TK besteht aus zwei Achsen von jeweils 5 Punkten und 4 Linien. Betrachtet man es als aus zwei konzentrischen Kreisen hervorgegangen, ist der Doppelaspekt von zweimal 5 Radialelementen und 9 Durchmesserelementen zu berücksichtigen:
|
|
|
Auf diesen Doppelaspekt weist die ZS 109 des TK hin.
Die ZS+FS der Zahlen von 1-25 beträgt 325+220 = 545 = 5*109. Der
Zusammenhang des Faktors 109 mit der Zahl 109 ergibt sich daraus, daß durch
Winkelverschiebung des AK3 das Qu3 hervorgeht und dieses aus 25 numerierbaren Elementen besteht: aus 9 Punkten + 4
Flächen (ungerade Zahlen) und 12 Linien (gerade
Zahlen):
|
|
Aufschlußreich sind die 4Werte
der 13 ungeraden und 12 geraden Zahlen:
|
|
ZS |
FS |
Diff. |
sm |
FW1 |
FW2 |
sm |
GS |
|
P+F |
169 |
133 |
36 |
302 |
26 |
26 |
52 |
354 |
|
L |
156 |
87 |
69 |
243 |
20 |
32 |
52 |
295 |
|
|
325 |
220 |
105 |
545 |
46 |
58 |
104 |
649 |
|
354:295 = 59*(6:5); 52
= 4*13 |
||||||||
|
36:69 = 3*(12:23) = 3*35 |
||||||||
Die zweimal gleiche FW1/2-Summe 52 = 4*13 verweist auf den
Tetraktysstern und jeweils vier
Doppeldreiecke zu je 13 Elementen zweier DR-Kreuze, aus
denen sich jeweils ein Oktaeder zusammensetzen läßt:
|
|
|
|
Ein DR-Kreuz besteht aus 29
Rahmenelementen bei einem und aus 30
Elementen bei zwei Mittelpunkten. 59 ist
auch die Numerierungssumme der 21 Elemente
einer einzelnen Doppelraute.
Schließlich ist an das Verhältnis der
Einzelziffern von 5:9
Durchmesserelementen zu denken, denen das Kreisflächenverhältnis 1:3 der beiden
Tetraktyskreise entspricht:
|
|
Die Aufteilung von 13+12 läßt sich auch auf 7
Punkte + 6 Flächen des Hexagons und 6 Punkte + 6
Flächen der hexagonalen Erweiterung beziehen. Es zeigt sich ein FS-Verhältnis
der Zahlen 1-13 und 14-25
von 11*(7:13). 7
Punkte des Hexagons und 13 Punkte des ganzen
Tetraktyssterns geben wiederum das Kreisflächenverhältnis 1:3 wieder.
Die Teilbarkeit beider Zahlenfolgen durch 13 ergibt sich daraus, daß 7 die Symmetriemitte von 13 und 13
die Symmetriemitte von 25 ist. Hier zeigt sich eine
der Übereinstimmungen zwischen numerischer Zahlenfolge des Dezimalsystems mit
systemrelevanten geometrischen Figuren.
Das oben
festgestellte Differenzverhältnis 3*(12:23)
= 105 läßt an das 1x1-Modell des SQ
denken, dessen Einzelziffern zusammen 105, deren
7 Einzelziffern ein Drittel der Summe
ergeben:
|
1 |
2 |
4 |
5 |
12 |
|
6 |
8 |
9 |
|
23 |
|
|
|
|
|
35 |
Erstellt: August 2020