Entwicklung
des Dezimalsystems
VI. Der
Tetraktysstern
A. Konstruktion,
Perspektiven
B. Beziehungen zw. Tetraktysstern u. Kreiselementen:
Numerierungen 49-56
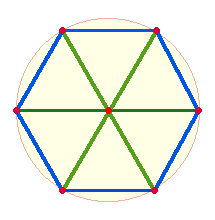
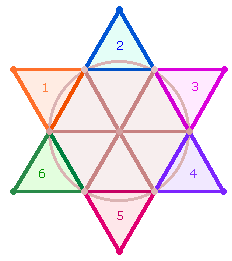
1. Die Erweiterung des Hexagon zum Tetraktysstern setzt
bisherige Konstruktionselemente fort: Die drei Hexagon-Achsen bestehen aus je zwei symmetrischen Radiallinien. Werden
die 6
Punkte des Kreisbogens durch Linien verbunden, entstehen 6 Dreiecke.
Das gesamte Hexagon kann so in das Verhältnis 6*(2:1) Radialmaße gefaßt werden:
|
|
Nun fehlt – analog zu drei hexagonalen Achsenpunkte –
noch eine zusammenhängende Strecke aus 3 Radialmaßen. Diese kommt zustande, indem man
über jedes Segementlinie mittels Zirkelschnittpunkte ein Dreieck errichtet, das
mit seinem spiegelbildlichen hexagonalen Dreieck eine Raute bildet. Auf diese
Weise erhält man 6 Strecken aus jeweils 3 Radialmaßen:
Zur Numerierung der Dreiecksseiten
siehe Berechnungen
der 6 Dreiecke.
Die 3
Hexagonachsen werden nun umschlossen von 2*3 = 6
Dreiecksseiten, die 2 symmetrisch verschränkte
Dreiecke bilden. Die 6 Segmentlinien sind nun
Zentraleinheiten mit je einem linken und rechten Seitenflügel.
Die Entstehung der Tetraktysseite wiederholt das
Flächenverhältnis der beiden
konzentrischen Kreise: 1:2 Radiallinien unter dem Erweiterungsaspekt und 1:3 Radiallinien unter dem getrennten Gesichtspunkt
eines hexagonalen Radialmaßes zu drei Maßen der Tetraktysseite.
Unter trinitarischem Gesichtspunkt ist die Zahl 3 die Summe der ersten 3 Ordinalzahlen (der 1.,2.,3.), die Zahl 6 die Summe der Kardinalzahlen von 1-3. Durch Addition 3+6 = 9 und Multiplikation 3*6 = 18 ergibt sich 27 = 3³.
Welche Bedeutung beide Zahlen haben, zeigt folgende
Überlegung und Untersuchung: Die Hexagonachse besteht aus 2 Linien+3 Punkten = 5 Elementen, die
Tetraktysseite aus 3 Linien+4 Punkten = 7 Elementen. Fügt man die jeweils 3 Zahlen zu
dreistelligen Zahlen zusammen und ermittelt von ihren je 6 Umkehrungen die Faktorenwerte (FW), ist
das Ergebnis 36*63:
|
|
2-3-5 |
FS
|
3-4-7 |
FS
|
GZS |
GFS |
||||
|
ZW |
235 |
325 |
523 |
|
347 |
437 |
734 |
|
2601 |
|
|
FW |
52 |
23 |
523 |
598 |
347 |
42 |
369 |
758 |
|
1356 |
|
ZW |
253 |
352 |
532 |
|
374 |
473 |
743 |
|
2727 |
|
|
FW |
34 |
21 |
30 |
85 |
30 |
54 |
743 |
827 |
|
912 |
|
|
|
|
|
683 |
|
|
|
1585 |
|
2268 |
|
2268 = 36*63 |
||||||||||
Die Zahlen 3 und 6 treffen kennzeichnen besonders den
Tetraktysrahmen, auf den hier schon vorgegriffen werden soll. Er besteht aus 3
Eckpunkten und 6 Hexagonalpunkte. Den einander gegenüberstehenden
Tetraktysrahmen entspricht in sinnvoller Weise die Umkehrungzahlen 36 und 63.
Die Zahlen der Tabelle sind in zwei Reihen angeordnet.
Die erste enthält die erste Zahl innerhalb einer Hunderterreihe, die zweite
deren Umkehrung. Die Gesamtzahlensumme 2727 weist auf die oben erwähnte Beziehung zu den Zahlen 3
und 6 hin, außerdem auf die Gleichwertigkeit der beiden konzentrischen Kreise:
Wenn jeder einen eigenen Mittelpunkt erhält, kommen zu je 25 Elementen noch die
Kreislinie und Kreisfläche hinzu. (Die Chöre von 27 Jungen und 27 Mädchen bei der Säkularfeier in Rom 17
v.Chr. könnte auf diese Gleichheit der beiden Kreise zurückzuführen sein.) Die
Zahl 2601 weist
durch ihre Einzelziffer auf den Tetraktysrahmen hin, ebenso 912 = 3*(4 Linien + 3
Punkte) der 3 Dreieckseiten.
Wie die Grafik zeigt, ergibt die Erweiterung des Hexagon zum Dreiecks- oder
Tetraktysstern 6 Rauten zu je 11 Elementen, zusammen 66. Die horizontale Mittellinie teilt die Rauten in 2*3 und 2*33 Elementen. Hierin ist ein Grund für den gleichen ZW 33 je Buchstabenhälfte des
römischen Hoheitstitels SP|QR zu vermuten.
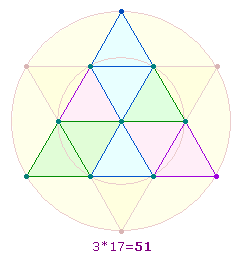
Wenn man andererseits nur eines der beiden Dreiecke
betrachtet, lassen sich von den Ecken her zu den 3 Rauten noch je ein Dreieck
hinzufügen. Eine dieser fischförmigen Figuren besteht aus 11+6 = 17 Elementen: 6 Punkten, 8 Linien, 3 Dreiecken. Die Zahl 683 ist die FS der 6 Umkehrungen von 235. Die FS der 6 Umkehrungen von 347 ist 1585 = 5*317. Die Primzahl 317 ist als 3*17 = 51 zu lesen.
|
|
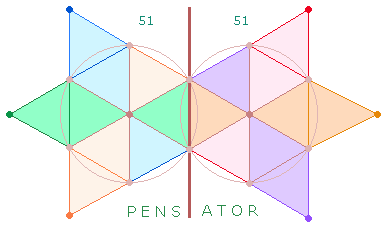
Nun besteht das Wort PENS|ATOR, das die 8 verschiedenen
Buchstaben des SATOR-Quadrats enthält, aus 2 Hälften mit jeweils den
gleichen ZW 51. Es scheint, daß die beiden symmetrisch zu
einander stehenden Tetraktys mit jeweils 3 Rauten bzw. 3 Fischfiguren ein
Vorbild für das SATOR-Quadrat gewesen sind. Gestützt wird diese Vermutung
dadurch, daß beide Hälften des Wortes PENS|ATOR sich noch einmal in je
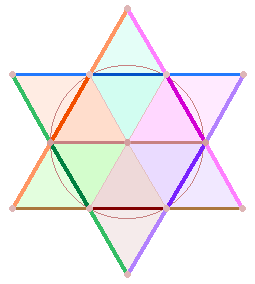
zwei Buchstabenpaare aufteilen läßt mit dem ZW 33 = 3*11 (PS-TO) und dem ZW 18 (NE-AR) = 3*6. Die folgende Grafik zeigt die 2*3
Fischfiguren auf zwei Hexagon auseinandergezogen:
|
|
2.
Ohne den Mittelpunkt besteht Gleichheit
der Elemente des Hexagon und der geometrischen Erweiterung: 6 Punkte, 6 Dreiecke, 12
Linien = 24, zusammen 48 Elemente. Nun muß man zum
Hexagon außer dem Mittelpunkt auch die Kreislinie und die Fläche als Elemente
hinzufügen. Denn der Kreiskonstruktion ist ja die Grundlage der weiteren
Einteilungen. Zu den genannten 24 Elementen des Hexagon kommen also noch 3 Kreiselemente hinzu. Die Elemente des Hexagon und der Erweiterung betragen
also 27+24 = 51. Dies ist deshalb bedeutsam, da ROTA – Rad den ZW 51 hat. Es ist daher anzunehmen, daß diesem ZW die
6 kreisförmig angeordneten Rauten bzw. Fischfiguren als geometrischem Modell
zugrundeliegen:
|
|
Die 51 Elemente des Dreiecksterns und 6*17 = 102 Elemente der Fischfiguren ergeben
zusammen 51*(1:2) = 153. Eine Beziehung zu den 153 bei Joh 21,11 erwähnten Fischen liegt
nahe.
3.
Die äußeren Dreiecke sind ohne
Kreislinie entstanden. Aber so wie aus dem Kreis das Hexagon entstand und
dieses sich über die Kreislinie hinaus zum Tetraktysstern entfaltet hat, bildet
der zweite Kreisbogen die logische Vollendung der gesamten Figuration.
Die Fläche des inneren Kreises verhält sich nun zum äußeren Kreisring 1:2 und zur Fläche des
ganzen äußeren Kreises 1:3. Diese beiden Verhältnisse, deren Addition 3+4 = 7 beträgt, bilden ein immer
wiederkehrendes Prinzip im Zahlengefüge des Dezimalsystems. In dem Beitrag Drei Doppelkreise der Dreifaltigkeit habe ich versucht, den trinitarischen Aspekt dieser beiden Verhältnisse
darzustellen.
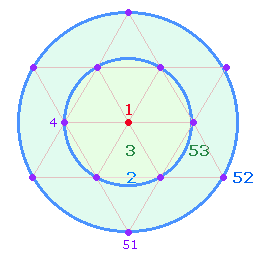
4.
Durch die Hinzufügung eines zweiten
Kreisbogens und Erzeugung einer weiteren Kreisfläche erhöht sich die Zahl der
Elemente des Dreieckssterns von 51 auf 53. Betrachtet
man die beiden Kreise als Zusätze zu den Unterteilungen des Dreieckssterns,
lautet die Rechnung für das Hexagon 25+2 und für die
Erweiterungselemente 24+2, zusammen 49+4. Nun ist es auffällig, daß die 3 Namen der Kapitolinischen Trias IUPPITER IUNO MINERVA den Zahlenwert (ZW) 252 und ihre Attributnamen OPTIMUS MAXIMUS
REGINA den ZW 242 haben. Ein Zusammenhang zu den Elementen des
Tetraktysstern liegt nahe.
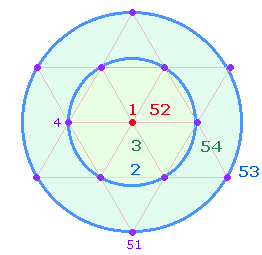
5.
Bei der Errechnung der 53 Elemente ist unberücksichtigt
geblieben, daß zur Ziehung des Kreisbogens der bestehende Mittelpunkt ein
zweites Mal benutzt wird. Damit erhält der äußere Kreis den Status der
Eigenständigkeit. Daher kann in einer zweiten Zählung ein weiteres Element, das
54. hinzugefügt werden
und jeder Kreis besteht aus 25+2 Elementen:
|
|
|
Die Relevanz dieses Doppelaspekts von 53 und 54 Elementen
kann in zahlreicher Weise durch Einbeziehung der Faktorenwerte (FW) und Anwendung der ZW/FW-Verrechnung überprüft werden. Ich wähle einiges davon aus:
–
Die einfachste Verrechnung ist die
der Zahlen 53 und 54 selbst:
|
|
ZW |
FW |
Sm. |
FW |
|
|
53 |
53 |
|
|
|
|
54 |
11 |
|
|
|
Sm. |
107 |
64 |
171 |
25 |
|
FW |
107 |
12 |
119 |
24 |
|
Sm. |
|
|
|
49 |
Zunächst ist die Summe der beiden Zahlen, die Primzahl 107, selbst
programmatisch, indem sie die 10 Punkte der Tetraktys und 7 Punkte des Hexagon darstellt. Die FW des Endergebnisses 25+24 entsprechen der
Zahl der Elemente des Hexagon und der Erweiterung ohne Kreiselemente.
–
Eine komplexere Verrechnung ist die
der ZS+FS der Zahlen 1-53 und 1-54:
|
|
1-53 |
1-54 |
Sm. |
FW |
||
|
|
ZS |
FS |
ZS |
FS |
|
|
|
|
1431 |
796 |
1485 |
807 |
4519 |
4519 |
|
FW |
62 |
203 |
25 |
272 |
562 |
283 |
|
Sm. |
|
|
|
|
|
4802 |
|
FW |
4802=2*2401
= 2*74 |
|||||
Das Produkt 2*2401 gibt die 24 Elemente des
Hexagon und der Erweiterung mit je 1 Mittelpunkt wieder. Die Faktoren 74 ergeben den FW 28, das entspricht der Summe der Punktenumerierung 1-7 für beide Kreiskonstruktionen.
Hier spielt auch das Flächenverhältnis
2:1 des äußeren Kreisrings zum inneren
Kreises eine bedeutsame Rolle. Denn das Verhältnis der Umkehrzahlen 21:12 ist 3*(7:4). Auch
die Zusammenfügung von jeweils 25 Elementen je
Kreiseinheit + 2 Kreiselementen (Bogen+Fläche) zu 252 = 12*21 kann hier angeführt werden.
Die Verrechnung jeder ZS und FS führt zu folgendem Ergebnis:
|
|
1-53 |
1-54 |
Sm. |
FW |
||
|
|
|
FW |
|
FW |
|
|
|
ZS |
1431 |
62 |
1485 |
25 |
|
|
|
FS |
796 |
203 |
807 |
272 |
|
|
|
Sm. |
2227 |
265 |
2292 |
297 |
|
|
|
FW |
148 |
58 |
198 |
20 |
|
|
|
Sm. |
206 |
218 |
8*53 |
59 |
||
|
FW |
2*103 |
2*109 |
6³ |
15 |
||
|
Sm. |
|
|
|
|
|
2*37 |
Die Faktoren 2*103 und 2*109 beziehen sich jeweils auf zwei Tetraktys: 10 Punkte +3 restliche
Eckpunkte des Tetraktyssterns und 10 Punkte + 9 Dreiecke der Tetraktys. Eine Tetraktys besteht aus 37 Elementen.
Die FW 148+198 = 346 = 2*173 weisen auf die 17 Elemente von 3 Fischfiguren in der Tetraktys hin.
–
Man kann die Numerierungen der
rechten Grafik (1-54) als dreistellige Zahlen behandeln: 152,
253, 354 und zusammen mit ihren Umkehrungen 521, 532, 543 verrechnen.
Eine zentrale Rolle
spielt naturgemäß der Mittelpunkt. Die Primahl 521 ist in ihren Einzelziffern zu verstehen als 5
Radialelemente (2+3 von außen her) des Doppelkreises
und ihre Flächenentsprechung 2:1. Faßt man 2+1 als Radialelemente des inneren
Kreises auf, bedeutet 5:(2+1) Radialelemente
das Flächenverhältnis 3:1.
Die Radialelemente 1+2 spiegelen sich auch in den FS der beiden
Mittelpunktszahlen und den 4 übrigen wider:
|
|
|
|
|
FS |
|
152 |
521 |
|
|
|
|
25 |
521 |
|
|
546 |
|
253 |
532 |
354 |
543 |
|
|
34 |
30 |
64 |
184 |
312 |
|
546:312 = 6*13*(7:4) |
||||
Das Verhältnis 7:4
weist wiederum auf die beiden Umkehrzahlen 12 und 21 hin, daneben vielleicht auf die 2*37 = 74 Elemente der beiden Tetraktys.
Ein gemeinsames
Teilungsverhältnis zeigen die ZS+FS der Umkehrzahlen:
|
|
|
|
Sm. |
Fkt. |
|
152 |
253 |
354 |
759 |
|
|
25 |
34 |
64 |
123 |
|
|
|
|
|
882 |
63*14 |
|
521 |
532 |
543 |
1596 |
|
|
521 |
30 |
184 |
735 |
|
|
|
|
|
2331 |
63*37 |
Die gemeinsame
Teilungszahl 63 =
3*21 verweist real auf
3 Doppelrauten zu je 21 Elementen. Aber auch ein Bezug zu 2*3
Radialelementen zeigt sich. Die Addition 14+37 = 51 zielt wohl auf die 51 Elemente des
Tetraktyssterns, aber auch die sich darin befindlichen 3 Fischfiguren. Die Zahl
14 bezieht sich auf 2*6+1 Punkte der inneren und äußeren
geometrischen Konstruktion bei je einem gemeinsamen Mittelpunkt.
–
Schließlich geben auch die ZS+FS der 5 Zahlen 50 bis 54 Aufschluß,
die als angehängte Kreiselemente gelten können:
|
|
|
|
|
|
Sm. |
|
50 |
51 |
52 |
53 |
54 |
260 |
|
12 |
20 |
17 |
53 |
11 |
113 |
|
|
|
240 |
373 |
||
|
240+373 = 613 |
|||||
Die Primzahl 373 gibt die Punkteveteilung des
Tetraktyssterns wieder. Beginnt man die Zählung ab 52 und rechnet die Summe 240 zu 373 hinzu, erhält man die Primzahl 613, die in ihren Einzelziffern der Punkteverteilung der Tetraktys entspricht.
Die Zahl 613 ist überliefert als Gesamtheit der
jüdischen Gebote, weswegen es nicht ausgeschlossen erscheint, daß die Tetraktys
auch der jüdischen Kulturwelt bekannt war.
Erstellt: 2007
Letzte Änderung:
März 2010