Das Buchstaben- und Zahlenmodell VESTA (II)
VIII. Die Bedeutung der Buchstaben VS
VIII.
Die Bedeutung der Buchstaben VS
1. Die Bu. V+S erhalten ihre hohe Bedeutung
durch die nominalen Ausgänge des Nom.Sg. der o- und u- Deklination. Ihre ZW 20 und 18 entsprechen am ehesten den 2*10 Punkten und 2*9 Dreiecken zweier gegenüber stehender
Tetraktys. Die ZS 38+FS 17 ergibt 55, die Summe der Zahlen von 1 bis 10.
Im Dezimalsystem
wirken 3
Obergrenzen zusammen, die Grundzahl 9, die Zahl 10 und die Zahl 11. Man kann sie als Begrenzungspunkte für je eine
Maßeinheit weniger betrachten, also 8,9,10. Das jeweilige Zahlenpaar von Begrenzungspunkten und
Maßeinheiten kann jedoch auch als komplementär zu den Zahlen 1+2 gesehen werden. Dann bilden die
Zahlen 10+9 = 19 die Mitte und 9+8 = 17 und 11+10 = 21 zwei symmetrische Außenseiten. Auf diese Weise entsteht
ein Verhältnis von 1:2. Die Buchstaben VS enthalten das eine addierte Zahlenpaar 9+8 = 17 als Faktorensumme (FS), und das andere 21
als Differenzwert zur Zahlensumme (ZS). Aus dieser Sicht ist der ZW 38 für DVO – zwei
sehr stimmig.
2. Die FS 17 für
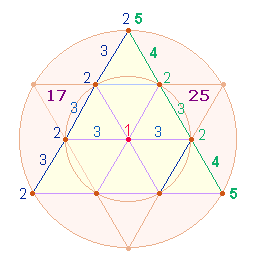
VS und 25 für ETA stimmen mit zwei
unterschiedlichen Numerierungen einer Tetraktysseite überein:
|
|
Die Numerierung der
Punkte (li. und re. Seite) ergibt 8+14 = 22 und
der Linien 9+11 = 20, zusammen das Verhältnis 2*(11:10), zu verstehen als 11 Begrenzungspunkte und 10 Maßeinheiten.
Vervollständigt
man die Numerierung für alle drei Tetraktysseiten, erhält man 4*42 = 126 und für 2 Tetraktys die
Umkehrzahlen 252 = 12*21. In den 2*(6+3) Sprechern und Adressaten der 9 Zeilen der Aeneis mit dem Wort ES finden diese Zahlenverhältnisse
eine konkrete Anwendung.
Bei der
Multiplikation der Tetraktysseiten mit 3 wird jeder Eckpunktwert doppelt gezählt. Möchte man die
Gesamtzahl aller numerierten Punkte errechnen, muß man 3*(2+5) = 21 von 126 abziehen
und erhält 105
(vgl. IV.d). Die durchschnittliche Zahl je
Seite ist 15 und 20, mit 3 multipliziert 45 und 60 im Verhältnis 3:4.
1.
Nimmt
man den ZW
63 als 3*21 und die 3 als
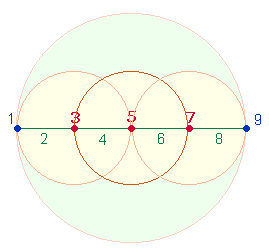
Radialelemente, bedeutet die Hinzufügung der FS 2*21 die Ergänzung zu 5 DM-Elementen. Die Summe 105 besteht aus den Faktoren 3*5*7, welche in der Skala von 1 bis 9 jeweils Mittelpunkte von Kreisen
besetzen und die Zahlen 1,2,3
symmetrisch verteilen. Auch der theologische Begriff TRINITAS – Dreifaltigkeit hat den ZW 105:
|
|
2. Wenn die Zahlen 1-9 durch Punkte
dargestellt werden, die 8 Maßeinheiten begrenzen, sind die Achsenpunkte des
SATOR-Quadrats 3-5-7.
3. Die Einzigartigkeit der Zahl 105 zeigt sich im selben ZW des
Wortes NVMERVS – Zahl,
das aus 7 Buchstaben mit einem
durchschnittlichen ZW von 15
besteht. Das E mit
dem ZW 5 steht in der Mitte wie in
Faktoren 3*5*7. Trennt man das Wort in 3+4 Buchstaben, ist auch das Verhältnis (3:4)*15 – in Übereinstimmung mit den
beiden Numerierungen unter IV.c). Trennt man NVMERVS in 4+3
Buchstaben, ist das Verhältnis 5*(10+11). Die jeweils gemeinsamen Teiler 15 und 5 stehen im Verhältnis 3:1. Auch das Wort TRI-NITAS trennt die Buchstaben 3 und 4 im identischen Verhältnis (45:60).
1.
Die
Buchstaben VA und EST verhalten sich nicht nur dem ZW
nach wie 1:2, sondern auch in der Addition der
übrigen 3 Werte:
|
|
ZS |
FS |
FW1 |
FW2 |
Sm. |
|
VA |
21 |
10 |
10 |
7 |
48 |
|
EST |
42 |
32 |
12 |
10 |
96 |
|
Sm. |
63 |
42 |
22 |
17 |
144 |
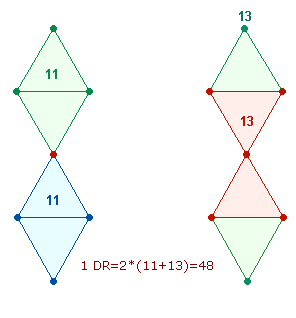
Die Zahl 48 setzt sich zusammen aus 2*(11+13) und bezieht sich auf die
Doppelraute: Verbindet man die Enden einer Doppelraute sind zwei geometrische Figuren
erkennbar: 2 Rauten mit je 11 Elementen und 2 Dreiecke mit gemeinsamem
Scheitelpunkt und 13 Elementen:
|
|
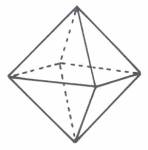
Der Oktaeder, der aus zwei Doppelrauten
zusammengesetzt ist, läßt entsprechend die doppelte Zahl von Dreiecksfiguren
erkennen:
|
|
Bemerkenswert
sind 22+26 als ZS der Initialen IN-RI und der Buchstabenzahlen der historischen und der biblischen Kreuzesinschrift.
XI.
2 DR-Verhältnisse 13:8
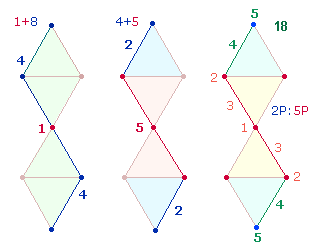
1. Der Bu. S mit dem ZW 18 bildet die
Wortmitte von VESTA. Er steht mit den ZW der übrigen
4 Buchstaben im Verhältnis 18:45 = 9*(2:5). Die Einzelziffern von 18 und 45 weisen auf die 9
DM-Elemente einer DR-Linie hin, 1+8 auf den MP + 2*4 symmetrische Elemente, 4+5
auf die 2*2 Elemente des äußeren Rings und die 5 DM-Elemente des inneren
Kreises, können aber auch 4L+5P zweier Kreisachsen bedeuten.
Die Verhältniszahlen 2 und 5 entsprechen den 7 Punkten der DR: 2 gehören dem äußeren Ring an, 5 den beiden Achsen des inneren Kreises.
Im Hinblick auf dieses Verhältnis gibt die Zahl 18 einen Hinweis auf die Numerierung der 9 DM-Elemente vom Mittelpunkt her:
die Radialelemente 4 und 5 ergeben verdoppelt 18:
|
|
2. Ein durch 3 teilbares Verhältnis erhält man,
wenn man die ZW der Bu. VSA und ET jeweils addiert:
|
V |
E |
S |
T |
A |
|
20 |
5 |
18 |
19 |
1 |
|
|
24 |
|
||
|
39 |
||||
|
39:24=3*(13:8) |
||||
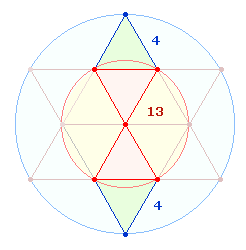
Die Zahl 13 bezieht sich auf die 13 Elemente des spiegelverkehrten
Doppeldreiecks in der DR, das dem inneren Kreis mit dem Flächenwert 1 angehört. Die DR wird
vervollständigt durch 2*4 = 8 Elemente, die Bestandteile des
äußeren Ringes mit der Flächengröße 2 sind. Dem Buchstabenverhältnis 3:2 entsprechen 3 Radialelemente des inneren
Kreises und 2 des äußeren Ringes. Fügt man Flächengrößen und
Radialelemente zusammen, erhält man 13+22 = 35 bzw. 31+22
= 53.
|
|
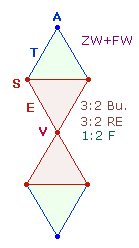
3.
Eine
buchstabengetreue Umsetzung der Verhältnisse 3:2 und 1:2 zeigt sich, wenn man ZW und FW von VESTA addiert:
|
|
V |
E |
S |
T |
A |
|
ZW |
20 |
5 |
18 |
19 |
1 |
|
FW |
9 |
5 |
8 |
19 |
1 |
|
Sm. |
65 |
40 |
|||
|
65:40=5*(13:8) |
|||||
Die beiden Verhältnisse 13:8 haben die Multiplikatoren 3 und 5. Sie können im Sinne
obenstehender Addition verstanden werden, aber auch als das Verhältnis der
Radialelemente des inneren und des ganzen äußeren Kreises. Das Verhältnis 3:5 der Radialelemente bezeichnet das
trinitarische Verhältnis 1:3 beider Flächen.
|
|
Erstellt: Juli 2005
Letzte Änderung: April 2006