Das Buchstaben- und Zahlenmodell VESTA
I.Das
Wesentliche
III. Das Differenzverhältnis zwischen Zahlenwert und
Faktorenwert
IV. Drei konzentrische Paare der Zahlen 1-20 und 1-21
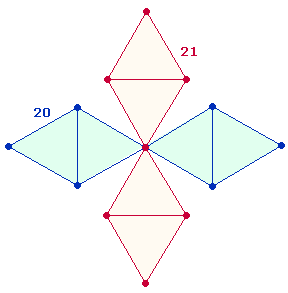
Zwei Tetraktys + eine Tetraktys (20+10)
VAT-ES,
VETAS, AVE ST; SOMNIUM SCIPIONIS
I. Das
Wesentliche
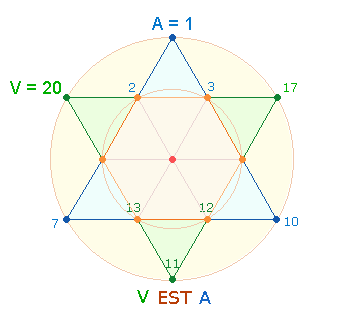
1. Der Name
V-EST-A gilt
etymologisch als ungeklärt. Die lautliche Beziehung zur griechischen Göttin des
Herdfeuers H-EST-IA ist jedoch unverkennbar und paßt gematrisch so gut zu VESTA, daß man von einer komplementären Konstruktion
sprechen kann. Wie ich auch an anderer
Stelle darlegte, verbirgt sich im Wort VESTA die Gleichung V EST A, d.h.
die von unten nach oben verlaufende Tetraktys ist gleich der von oben nach
unten verlaufenden:
|
|
Die
Zahlen 1 und 20 als numerische Grundlage
von A und V legen eine konzentrische
Betrachtungsweise der Zahlen
1-20 nahe. Tatsächlich entsprechen die
Buchstaben VESTA genau den drei ersten und drei letzten
Zahlen, dem Buchstaben E liegt die Addition 2+3 = 5 zugrunde:
|
ZW |
1 |
2 |
3 |
4-17 |
18 |
19 |
20 |
|
Bu. |
A |
E |
|
S |
T |
V |
|
AESTV ist Ablativ zu AESTUS – Hitze, Glut, Feuer und
steht so in einem inneren Bezug zum Kult der Vesta (dazu einige
Gedanken). Die Bedeutung der Zahl 20 zeigt sich darin, daß der Rundtempel der
VESTA in Rom von 20 Säulen umkränzt war. Durch Vertauschung
des ersten und letzten Buchstabens wurde schließlich die Endform VESTA erreicht.
Freilich ist die Frage zu klären, wie es zum Tausch der
Buchstaben A und V kam. Der wesentliche Grund, den die Römer erkannten, liegt
in einem allgemeinen Prinzip der Beziehung zwischen Gott und Mensch:
Menschliche Kultur entwickelt sich immer in der Beteiligung menschlicher
Freiheit an den Vorgaben göttlicher Weisheit, die auf diese Weise gleichsam
erst ihre Vollendung findet. Was menschlichen Geist gedrängt hat, den
Buchstabentausch vorzunehmen, kann verschiedene Gründe haben. Einer ist
sicherlich, daß das Ende vom Anfang her und der weniger bekannte Begriff durch
einen bekannteren zu definieren ist, ein zweiter, daß jede mathematische
Gleichung aus zwei gleichen Teilen besteht. Die Urgleichung ist 3 = 1+2. Jede
Teilung eines Ganzen kann in eine Gleichung gefaßt werden.
Als weiterer Grund ist denkbar, daß bei der Umwandlung eines Doppelrautenkreuzes zu einem Oktaeder das untere V-Dreieck
(der vertikalen) Doppelraute bei seiner Faltung und Drehung zum oberen Endpunkt
der Doppelraute zur Umkehrform A wird. Denn der Oktaeder ist als
Vollendung des geometrischen Modells des Dezimalsystems anzusehen.
Auch der griechische H-EST-IA Kult könnte das Bedürfnis nach einem parallelen Kult in Rom
geweckt haben. Die Buchstaben EST könnten
als providentielle Vordeutung in diese Richtung gewirkt haben.
Zu bedenken ist auch, daß erst im 3. Jahrhundert v. Chr. die
Diphthongschreibung AE statt AI verwendet wurde, weswegen erst dann A-EST-V im Sinne von AESTU gelesen werden konnte.
2. Die
Zahlensumme (ZS) der 5 Buchstaben ist 3*(20+1)= 63. Die
Zusammensetzung der 5 Buchstaben aus
einer konzentrischen Zahlenreihe bringt es mit sich, daß die äußeren 2 Buchstaben VA und die inneren 3 Buchstaben EST das Zahlenverhältnis 21:42 = 21*(1:2) bilden.
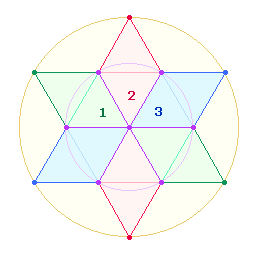
Der
engste inhaltlicher Bezug der 5 Buchstaben ist in den 3 Doppelrauten zu
sehen, von denen jede aus 21
Elementen (7 Punkten, 4 Dreiecken, 10 Linien)
besteht:
|
|
3. Eine
besondere Bedeutung gewinnt der Begriff VESTA darin,
daß ein Verhältnis zwischen Faktorensumme (FS) und
Zahlensumme besteht:
|
|
V |
E |
S |
T |
A |
sm |
|
ZW |
20 |
5 |
18 |
19 |
1 |
63 |
|
FW |
9 |
5 |
8 |
19 |
1 |
42 |
|
42:63 = 21*(2:3) |
105 |
|||||
Die FS 42 = 2*21 kann man auf die Rahmenelemente der zwei Tetraktys
des Sechsecksterns beziehen: Jede Dreiecksseite besteht aus 4 Punkten und 3
Maßeinheiten. Auf diese Weise wird die Dreiheit der Doppelrauten mit der
Zweiheit der Tetraktys verbunden:
|
|
Die Zahl von 5 Buchstaben, deren
durchschnittlicher ZW+FW 21 beträgt, führt zu Grundverhältnissen des Kreises.
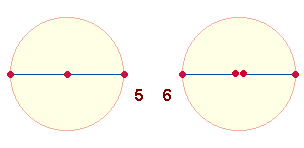
1.
Eine
Kreisachse besteht aus 2 Radialmaßen, die jeweils von 2
Punkten begrenzt wird, demnach aus 3+3
Radialelementen. Das zeigt sich auch in der Schreibung des ZS-Verhältnisses von AV:EST = 21*(1:2).
Der Mittelpunkt ist also doppelt zu rechnen.
In Wirklichkeit hat der Durchmesser (DM) nur einen Mittelpunkt und besteht
somit aus 5 DM-Elementen.
Daraus ergibt sich der Doppelaspekt
von multiplikativem 2*3
und additiven 3+2:
|
|
Diesem Doppelaspekt wird im Namen VESTA wohl darin Rechnung getragen, daß
das E aus den zwei Zahlen 2+3 besteht.
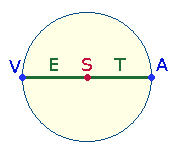
2.
Die
5 Buchstaben von VESTA können nun auf die DM-Elemente gesetzt werden:
|
|
Die beiden Radiallinien zeigen durch das lateinische
Bindewort ET
ihre verbindende Funktion. Es ist auch im TENET-Kreuz des SATOR-Quadrats enthalten.
Die ZS
der Buchstaben der 3
Punkte VSA und der 2 Linien ET sind jeweils durch deren Anzahl
teilbar: 39:3 = 13, 24:2 = 12.
III. Das Differenzverhältnis zwischen
Zahlenwert und Faktorenwert
1.
Der
Faktorenwert (FW) einer Primzahl ist mit dieser
identisch, ZW+FW ist also zu verdoppeln, z.B. 5+5.
Bei Nicht-Primzahlen gibt es eine Differenz zwischen FW und ZW. Der FW von 8 z.B. ist 6, das FW:ZW-Verhältnis
ist daher 6:8 = 2*(3:4).
Das Differenzverhältnis von FW
und ZW ist jedoch 3:1.
Auf das Wort VESTA übertragen ist das externe FS:ZS-Verhältnis
21*(2:3), das interne Verhältnis 2:1. Das externe Verhältnis
entspricht den 5
DM-Elementen, das interne den 3 Radialelementen.
Man wird also die ZS 63
zunächst auf die 3 Radialelemente verteilen und nach
dem Zuwachs der FS
auf alle 5
DM-Elemente. Kriterium der Buchstabenaufteilung ist das ZS-Verhältnis 1:2 der Bestandteile VA:EST:
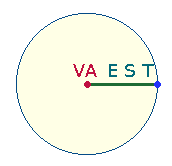
Internes und externes Verhältnis von VESTA bilden wiederum ein Verhältnis 3:5.
Dieses ist kennzeichnend für die Radialelemente der beiden Tetraktyskreise, die
nach dem Analogprinzip das Flächenverhältnis 1:3 wiedergeben.
IV. Drei
konzentrische Paare der Zahlen 1-20 und 1-21
1. Konzentrische Zahlenpaare ergänzen
sich zu einer Summe, die stets um einen Zähler höher als die Endzahl ist (1+20 = 21). Die Summen der Zahlenpaare zweier
aufeinanderfolgender Endzahlen haben stets denselben
Multiplikationsfaktor und ergeben die Quadratzahl der höheren Endzahl. Im Falle
der Zahlen 20 und 21 setzt sich die Summe zusammen
aus:
10*21+ (10+1)*21 = (10+11)*21 = 21² = 441.
Die Einzelziffern
der Endsumme 441
zeigen die 9 Durchmesserelemente des
Tetraktyssterns.
Die beiden Zahlen 21 und 20 sind für den Tetraktysstern
insofern von wesentlicher Bedeutung, weil ein Doppelrautenkreuz bei einem
Mittelpunkt aus 21+20
= 41 Elementen besteht:
|
|
Der konzentrischen
Betrachtungsweise ist dadurch Rechnung getragen, daß komplementär ein DR-Kreuz mit 3
Mittelpunkten
zu denken ist, das somit aus 21+22 Elementen besteht.
2. Fügt man zur Zahl 441 noch die FS 155+165 = 320 hinzu, erhält man als Endsumme die Primzahl 761, deren Einzelziffern die (7+6)+1 Punkte des Tetraktyssterns mit seinen zwei konzentrischen
Kreisen wiedergeben. Der zusätzliche Punkt ist der Mittelpunkt für den äußeren
Tetraktyskreis.
3. Das Erstaunliche an den beiden
Zahlen 20 und 21 ist, daß die drei ersten
konzentrischen Zahlenpaare jeweils das FS:ZS-Verhältnis 2:3 haben:
|
ZW |
1 |
2 |
3 |
|
18 |
19 |
20 |
63 |
|
FW |
1 |
2 |
3 |
|
8 |
19 |
9 |
42 |
|
ZW |
1 |
2 |
3 |
|
19 |
20 |
21 |
66 |
|
FW |
1 |
2 |
3 |
|
19 |
9 |
10 |
44 |
Der formale Grund
ist leicht zu erkennen: Die Zahlen- und FW-Differenz von 21 gegenüber 18 ist 3+2. Das
addierte FS:ZS-Verhältnis ist nun 86:129 = 43*(2:3) = 215.
Erstaunlich ist weiterhin, daß die
ersten beiden Wörter des SATOR-Quadrats SATOR OPERA ebenfalls die ZS+FS 215
haben:
|
|
ZS |
FS |
sm |
|
SATOR |
69 |
54 |
123 |
|
OPERA |
52 |
40 |
92 |
|
|
121 |
94 |
215 |
Von Interesse sind auch die ZS+FS der inneren 3 Zahlenpaare:
|
ZW |
8 |
9 |
10 |
11 |
12 |
13 |
63 |
|
FW |
6 |
6 |
7 |
11 |
7 |
13 |
50 |
|
ZW |
9 |
10 |
11 |
12 |
13 |
55 |
|
FW |
6 |
7 |
11 |
7 |
13 |
44 |
Die ZS+FS sind 118+94 = 212. Das FS:ZS-Verhältnis der äußeren und inneren Zahlenpaare beträgt (86+94):(129+118) = 180:243 = 9*(20:27) = 9*47 = 423.
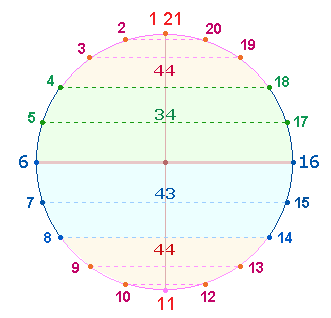
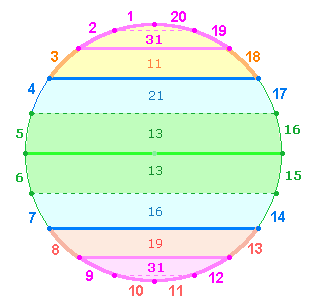
4. Die konzentrische Betrachtungsweise
einer fortlaufenden Zahlenreihe kann man am besten in Kreisform darstellen:
|
|
|
Die beiden Grafiken
sind als komplementär anzusehen: Die Zahlen 1-21 sind den Punkten, die Zahlen 1-20 den dazwischenliegenden
Segmentlinien zugeordnet. Die eingetragenen Werte sind FS von Zahlenpaaren.
Der Kreis wird
geteilt durch die Mittelachse 6-16,
welche beiden Hälften angehört. Ohne die Mittelachse befinden sich in der
oberen Hälfte 20, in
der unteren 19 Zahlen. Die Ordnung der beiden Zahlenmodelle wird am
besten an den FS
erkennbar:
|
|
|
1-21 |
1-20 |
sm |
6-16 |
GS |
|
FS |
o.H. |
78 |
76 |
154 |
13 |
167 |
|
FS |
u.H. |
74 |
79 |
153 |
13 |
166 |
|
|
|
|
|
307 |
|
333 |
Die angrenzenden FS 167 und 166 stellen eine optimale Symmetrie
der beiden Hälften wieder. Die beiden Zahlen sind nicht nur konstitutiv für
ihre Summe 333, sondern interpretieren in ihren
Einzelziffern und auf die Punkte bezogen zwei Aspekte des Tetraktyssterns, 166 ohne und 167 mit einem zweiten Kreis, der die
Rückkehr zum Mittelpunkt erfordert. Die Summe ihrer FW 85+167 = 252 =
12*21 bildet mit 333 das Verhältnis 9*(28:37). Die FS 167 ist zugleich Umkehrzahl zu 761 (s.o.).
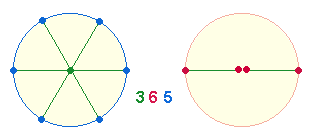
Die FS der beiden
ganzen Kreise 320,
und die der Hälften 333
ergeben die Gesamtsumme 653, eine Primzahl, die den
Doppelaspekt von 6
Radialelementen und 5
Durchmesserelementen des 3-achsigen
Hexagons wiedergibt:
|
|
s.a. vertiefende
Erörterung des Wortes EST; konzentrische Zusammensetzung der 6
Zahlen. Das Gleichungsprinzip ist auch in der Kapitolinischen Trias und den Verssummen der 10
Eklogen Vergils verwirklicht.
Erstellt: Juli 2005
Letzte Änderung: März
2013