Deutung der fehlenden Elemente 43 und 61 nach d. Gesetzen d. Dezimalsystems

125:240 = 5*(25:48) = 365 = 5*73

Die fehlenden stabilen Elemente 43 und 61

I. Einleitung

II. Deutung der Zahlen 43 und 61

III. Doppelaspekt

IV. Dreiteilung

a) Gesamt

b) Einzelabschnitte

V. Innere und äußere Glieder

VI. Drei Zahlenebenen

Ineinanderfügung der drei Ebenen

I. Einleitung

1. Zu den Chemikern, die das Dezimalsystem nicht als eine menschliche Erfindung, sondern als naturimmanente Wirklichkeit begreifen, gehört Peter Plichta, der darüber ein dreibändiges Werk "Das Primzahlkreuz" veröffentlicht hat.

Ich bin nicht nur kein Chemiker, sondern der chemischen Wissenschaft völlig unkundig. Mir scheint jedoch, ich könnte einen ontologischen Beitrag leisten, der das Fehlen der Elemente 43 und 61 einigermaßen verständlich macht. Es geht in erster Linie um das Aufzeigen von Zahlenperspektiven und erst in zweiter Linie um mögliche Deutungen. Es bleibt den in der Chemie Bewanderten überlassen, ob sie daraus neue Erkenntnisse gewinnen können.

Auf zu detaillierte Weiterverrechnungen einzelner Ergebnisse soll um der Übersichtlichkeit willen – mit einer Ausnahme – verzichtet werden.

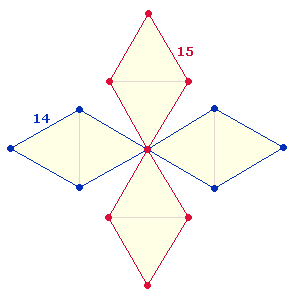
2. Betrachtet man die Schöpfung als Abbild des dreifaltigen Gottes, ist die Einheit in der Dreiheit im Kreis grundgelegt. Denn der Kreis ist definiert durch Mittelpunkt, Kreisbogen und Fläche. Nur alle drei Bestandteile zusammen lassen die Einheit einer Form erkennen.

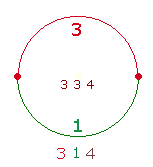
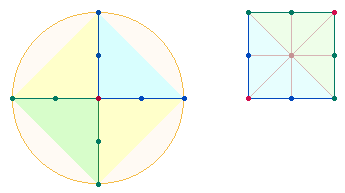
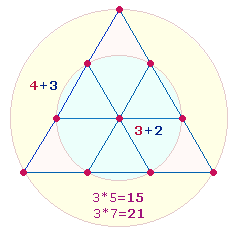
In der Tat läßt sich die Zahl 10 und damit das Dezimalsystem bereits erkennen, wenn man den Kreisbogen durch zwei Punkte teilt, wodurch vier Elemente zustande kommen, zwei Punkte und zwei abgeteilte Kreislinien:

Eine Kreisbogenhälfte definiert sich aus Kreislinie und zwei Punkten, für die zweite Hälfte bleibt eine Kreislinienhälfte übrig. Betrachtet man jede Hälfte als eigenständig, bestehen die Ganzheit und die Hälften aus 4+3+3 = 10.

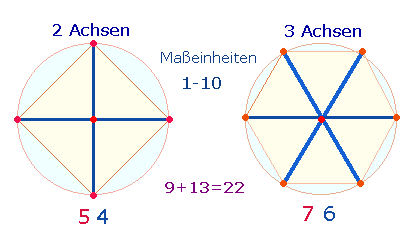
In weiterer Differenzierung des Kreises wird das System der Zahlen durch zwei und drei Achsen bestimmt:

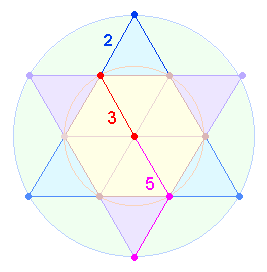
Aus der linken Figur entwickeln sich endlos vergrößerbare Quadrate, aus der rechten lediglich das Hexagramm mit zwei Tetraktys und drei Doppelrauten, von denen zwei zu einem Achsenkreuz gebildet und dieses zu einem Oktaeder zusammengefügt werden kann.

3. Das Dezimalsystem ist so beschaffen, daß einzelne Zahlen auch in mehrstelligen Zusammensetzungen ihre Grundbedeutungen bewahren.

4. Das Dezimalsystem aus seinem ontologischen Ursprung habe ich in einem grundlegenden Kapitel dargelegt. In Berechnungen sind unerläßlich Faktorenwerte (FW) einzubeziehen.

II. Deutung der Zahlen 43 und 61

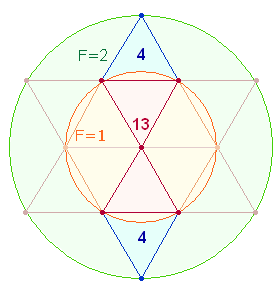
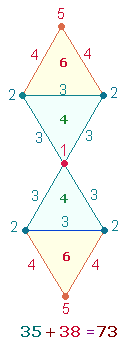
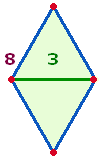
1. Die Zahlen 43 und 61 sind aus ihrer Summe 104 = 13*8 zu verstehen und auf die Doppelraute (DR) zu beziehen:

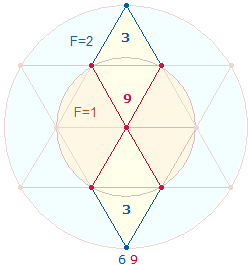
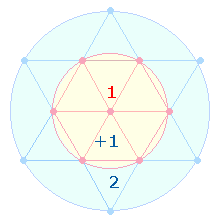
Das Flächenverhältnis des hexagonalen Kreises zum äußeren Kreisring ist 1:2 und wird durch 13 Elemente des hexagonalen Doppeldreiecks und seiner Erweiterung um 8 Elemente wiedergegeben.

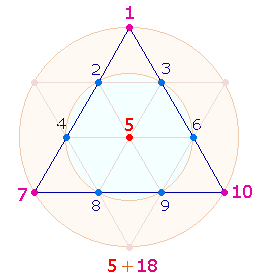
2. Ausgehend von dem Produkt 13*8 sind die Zahlen 43 und 61 als Einzelziffern zu interpretieren und auf die Punktestruktur der Doppelraute zu beziehen, die nach obiger Darstellung aus 4 horizontalen und 3 vertikalen Punkten besteht sowie aus 2*3 spiegelbildlichen Punkten und dem Mittelpunkt.

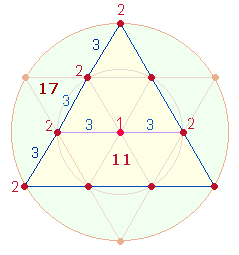
Die Einzelziffern 4+3 und 6+1 kennzeichnen auch eine einzelne Tetraktysseite. In der ersten Kombination werden 3 Maßeinheiten durch 4 Punkte begrenzt, in der zweiten werden 3 Punkte und 3 Maßeinheiten zusammengefaßt und durch den vierten Punkt abgeschlossen. Der letzte Punkt gehört eigentlich bereits zur nächsten Seite, sodaß sich die Doppelzählung 3*7 = 21 und 3*6 = 18 ergibt.

3. Die Ordnungen der Chemie erscheinen demnach in die grundlegenden Modelle des Dezimalsystems eingebunden.

III. Doppelaspekt

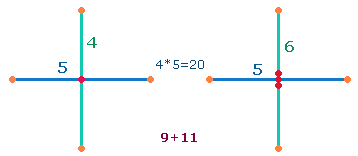
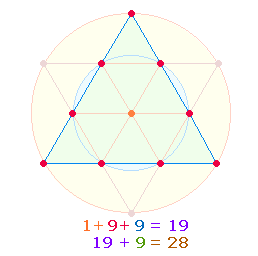
1. Durch das Fehlen zweier stabiler Elemente kommt der Doppelaspekt von 81 stabilen Elementen und der Ordnungszahl 83 zustande. Als Einzelziffern verstanden, lassen sich aus den beiden Zahlen zwei Achsenkreuze bilden:

Eine Achse besteht aus 5 Elementen. Um diese Durchschnittszahl zu erhalten, ist ein zweites Achsenkreuz zu denken, dessen zweite Achse aus zwei Mittelpunkten besteht. Es ist in diesem und erweiterten Achsenkreuzen das Prinzip 1:3 zu erkennen.

2. Jede Zahl ist konstituiert aus der Summe zweier angrenzenden Zahlen (ungerade Zahl) oder zweier durch eine Zahl getrennter Zahlen (gerade Zahl). Die Zahlen 81 und 83 begründen daher die Summenzahl 164, die im DR-Kreuz auf folgende Weise anzutreffen ist:

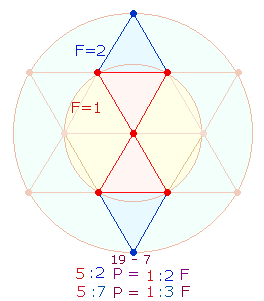
Die Doppelraute enthält drei verschiedene geometrische Figuren, die von der jeweiligen Spitze her gesehen werden können:

Je Doppelraute kann man also 82 Elemente errechnen, die sich im DR-Kreuz auf 164 verdoppeln.

3. Die Zahl 83 gewinnt ihre besondere Bedeutung darin, daß sie sich aus 28+55 zusammensetzt, das sind die Summen der Zahlen 1-7 und 1-10. Aus 7 Punkten besteht das Hexagon, aus 10 Punkten die aus dem Hexagon hervorgehende Tetraktys.

IV. Dreiteilung

a) Gesamt

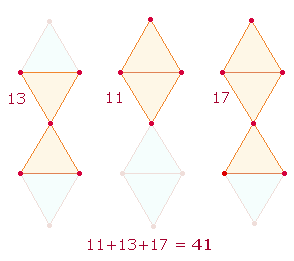
1. Die fehlenden Elemente 43 und 61 teilen die 81 stabilen Elemente in drei Zahlenreihen:

1-42, 44-60, 62-81 bzw. 42+17+22.

Die ZS+FW der drei Zahlengruppen sind:

Zahl	42	17	22	81
FW	12	17	13	42
	54	34	35	123
	54	69

Das Differenzverhältnis zwischen Faktorensumme (FS) und Zahlensumme (ZS) beträgt 42:39 = 3*(14:13). 54 ist zu verstehen als 6*9, 69 als 6*9+(6+9). Die beiden Zahlen betreffen insbesondere 15 Rahmenelemente der DR:

9 Rahmenelemente gehören dem hexagonalen Bereich, 6 dem Erweiterungsbereich an. Die 9:6 Rahmenelemente vertreten wiederum das Kreisflächenverhältnis 1:2. 6 ist gleichzeitig der FW von 9, sodaß das interne Differenzverhältnis 3*(2:1) beträgt, genau dem Kreisverhältnis entsprechend.

Eine Entsprechung der Zahlen 69 und 54 findet sich in dem Wort SATOR – Schöpfer des SATOR-Quadrats; erstere ist die ZS, letztere die FS.

Der Summe 123 entsprechen die ZS und FS der Zahlen 1-11: 66+57 = 123. Das Hexagramm enthält 6 Rauten zu je 11 Elementen.

2. Die ZS+FS der Zahlen 1-83 beträgt 3486+1738 = 5224 = 48*109. Die Zahl 48 ist zu verstehen als 2*(11+13). Ein Oktaeder läßt sich zusammengesetzt denken aus den Elementen von zwei Rauten und zwei hexagonalen Doppeldreiecken.

Von der Summe 5224 ist die ZS+FS 2*(43+61) abzuziehen. Die Faktoren des Subtraktionsergebnisses 5016 sind 24*11*19. Die Faktoren 109 und 19 sind beide als 10 Radial- und 9 Durchmesserelemente des Hexagramms interpretierbar und als Achsenkreuz darstellbar. Dasselbe trifft auf die Zahl 11 (6+5) des hexagonalen Kreises zu:

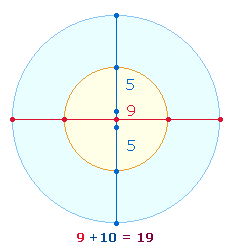
Im Hinblick auf die beiden konzentrischen Kreise des Hexagramms vertreten die Zahlen 11 und 19 das Kreisflächenverhältnis 1:3.

3. Berechnet man ZS und FS gesondert, sind beide Ergebnisse nach Abzug von jeweils 104 durch 2*19 teilbar:

ZS	3486	-104	3382
FS	1738	-104	1634
1634:3382 = 38*(43:89)

Der Verhältnisausdruck 38*(43:89) weist auf die Tetraktys hin: Die Zahl 19 kann man einer Tetraktys zweimal zuordnen: Sie enthält erstens 10 Punkte und 9 Dreiecke, und besteht zweitens aus 18 Rahmenelemente der drei Tetraktysseiten und dem Mittelpunkt. In dieser Doppelzählung sind die Punkte zweimal vertreten.

Die Einzelziffern der Zahlen 43 und 89 beziehen sich auf 4 Punkte und 3 Linien einer Tetraktysseite, 8 und 9 bei deren Numerierung mit 2 und 3:

4. Wählt man nur 19 als gemeinsamen Faktor, sind die Verhältniszahlen 86 und 178. Die Zahl 86 bezieht sich auf das DR-Kreuz in dreifacher Weise:

– Die Interpretation 2*(4+3) bezeichnet zweimal 7 Punkte je DR.

– Der DR-Rahmen besteht aus 8 Linien und 7 Punkten. Bei der Oktaederbildung verbinden sich die beiden äußeren Punkte der DR zu einem Punkt, woraus sich 8+6 ergibt.

– Die DR besteht aus zwei Zickzack-Linien, die vier Dreiecke und zwei Querlinien einschließen. Die 9 Elemente der DR können entsprechend links, rechts und in der Mitte gezählt werden. Bei der Vereinigung der beiden äußeren Punkte entfällt 1 Punkt, so daß im DR-Kreuz die Zahl 8 6-mal zu zählen ist.

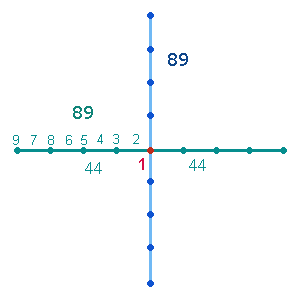
Numeriert man einen Achsenarm aus 9 Elementen vom Mittelpunkt zweimal zum Rand, ist die Summe einer Achse 89, die sich durch eine zweite Achse zur Summe 178 verdoppelt:

b) Einzelabschnitte

1. Die drei Abschnitte ergeben folgende ZS+FS:

Gr.	Prod.	ZS	FS	sm
1-42	21*43	903	528	1431
44-60	17*52	884	389	1273
62-83	11*145	1595	717	2312
sm		3382	1634	5016
1431 = 2753; 1273 = 1967
2312 = 8*17²

Die ZS+FS der mittleren Zahlengruppe ist durch 19 teilbar, wodurch die beiden äußeren Gruppen komplementären Charakter erhalten.

2. In Verbindung mit der Zahl 19 ist auch die Zahl 67 als ein Achsenkreuz mit drei Mittelpunkten zu verstehen:

Beide Achsenkreuze bestehen aus 4*20 = 80 symmetrischen Elementen + 6 Mittelpunkten.

3. Die FW der drei Zahlengruppen sind:

ZS/FS	903	528	884	389	1559	717	5016
FW	53	22	34	389	45	242	785
sm							5801

Die Summe 5801 ist eine Primzahl (PZ) und als 58+1 zu verstehen. Die Summe 59 kommt durch Numerierung der DR von 1-4 zustande:

V. Innere und äußere Glieder

a) innere Glieder

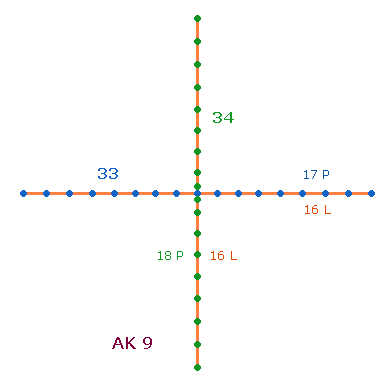
1. Die Mittelpunktszahlen der ersten und dritten Zahlengruppe, die sich als komplementär erwiesen haben, sind 21+22 = 43 und 72+73 = 145; 43+145 = 188 = 4*47. Die beiden Summen weisen auf ein unnumeriertes und ein numeriertes DR-Kreuz hin, ersteres mit 3 Mittelpunkten, letzeres mit 1 Mittelpunkt. Die folgende Doppelraute steht für das numerierte DR-Kreuz aus 73+72 Elementen:

Die Numerierung des hexagonalen Bereiches geht von 1-4, der Erweiterungsbereich von 4-6. Im DR-Kreuz ist die Zahl der Erweiterungselemente von 38 auf 76 zu verdoppeln. Unnumeriert betragen die Erweiterungselemente 16. Ohne Mittelpunkte sind für den hexagonalen Bereich zweimal 34+12 = 46 zu zählen, sodaß sich für beide Bereiche die Summe 92 ergibt. Fügt man zum hexagonalen Bereich noch die 3+1 Mittelpunkte hinzu, erhält man das Verhältnis 4*(24:23).

Die Zahl 92 bezieht sich u.a. auf ein Quadrat, dessen vier Seiten aus je 2 Maßeinheiten und 3 Punkten besteht und aus einer Winkelverschiebung des Achsenkreuze Ak3 zustande kommt:

Das 3*3 Punkte-Quadrat ist das erste mit Diagonalachsen. Das dargestellte Achsenkreuz läßt sich aus 1+8+8 Elementen zusammensetzen, weist aber mit der Zahl 188 = 4*47 auf das nächst größere Achsenkreuz hin.

2. Die Innenglieder der drei Zahlengruppen liefern folgende ZS+FS:

Die Zahlen des internen Verhältnis 25:23 sind die Konstitutivzahlen für die Summe 48. Die Einzelziffern des Produkts 5*73 sind auf die Achsenelemente des Hexagons und Rahmenelemente der Tetraktys zu beziehen:

Natürlich wird man eine Beziehung zu den 365 Tagen des Jahres nicht ausschließen.

b) äußere Glieder

1. Das Vorbild jeder Zahlenreihe sind die 5 Durchmesser- und 2*3 Radialelemente. Die zwei Außenglieder einer konzentrischen Betrachtung entsprechen den zwei Kreislinienpunkten, die zwischen den Punkten liegenden Zahlen den Radiallinien.

Die 6 Rahmenzahlen sollen nach unterem und oberen Ende unterschieden werden:

	unten			sm	oben			sm	GS
Zahl	1	44	62	107	42	60	83	185	292
FW	1	15	33	49	12	12	83	107	156
sm				156				292	448

2. Zwei Teilsummen, eine als ZS, die andere als FS, betragen 107, mit zweimal der Folgesumme 156. Die Primzahl 107 weist auf 10 Punkte der Tetraktys und 7 Punkte des Hexagons hin. Die Einzelziffern des Produkts 12*13 = 156 sind auf die trinitarischen Kreisflächenverhältnisse der beiden Tetraktyskreise zu beziehen.

3. Die Gesamtsumme 448 könnte als additiver Aspekt des Produkts 16*28 ein quadratisches Pendant zu den drei Seiten der Tetraktys darstellen: Das Verhältnis 16:28 ist 4*(4:7) vergleichbar zu 12:21 = 3*(4:7): Die 4 Punkte einer Seite werden in Bezug zur Gesamtheit von 7 Elementen gesetzt.

c) Gesamtsummen

1. Die ZS+FS der inneren und äußeren Glieder sind:

	ZS	FS	sm
inn.	240	125	365
auß.	292	156	448
sm	532	281	813
813 = 3*271
532 = 19*28

Die Gesamtsumme 813 entspricht in dem Produkt 8*13 = 104 der Addition 43+61 der Ausgangssituation. Die Primzahl 271 ist zu verstehen als 27+1: 27 ist die Summe der Zahlen 2-7 und bezieht sich auf 2*3 Punkte der Doppelraute, die Zahl 1 stellt den Mittelpunkt dar. Der Faktor 3 verweist auf drei DR des Hexagramms.

2. Die Einzelziffern der ZS 532 bezeichnen die 10 Radialelemente der Doppelraute:

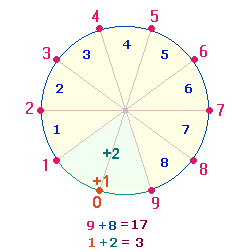
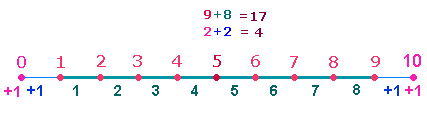
Das Produkt 19*28 weist auf das Grundmodell der Zahlen 1-10 hin:

Die Grundzahlen 1-9 müssen durch den Punkt 0 ergänzt werden, wodurch 2 Maßeinheiten hinzukommen. Die Zahlen 9 und 8 sind komplementär zu 1 und 2 zu verstehen und haben trinitarische Bedeutung im Sinne 1+2 göttlicher Personen. Die dreistelligen Zahlen 173 und 317 sind Primzahlen.

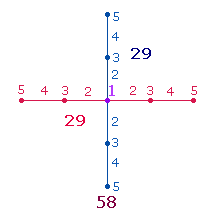
3. Die Primzahl 281 mit identischem FW ist zu lesen als 28+1. Sie entsteht durch Numerierung einer Achse vom Mittelpunkt aus mit den Zahlen 1-5:

Nun zeigt sich überraschend, daß die ZS 532 und ihr FW 30 mit der Summe 562 ebenfalls 2*281 beträgt. Damit könnte eine Verbindung zwischen dem Achsenkreuz Ak3 und dem DR-Kreuz hergestellt werden, dessen Rahmen aus 29 Elementen besteht. Es müßte also noch ein zweites DR-Kreuz hinzukommen:

d) Die zwei Mitten

1. Die drei Punkte des Kreisdurchmessers bilden eine Einheit gegenüber den beiden Radiallinien. Von den drei Zahlenreihen entsprechen dem Mittelpunkt 5 und den äußeren Punkten 6 Zahlen. Von 81 bleiben demnach 70 übrig. Die ZS+FS der 11 Zahlen beträgt, wie oben dargestellt, 813, die ZS+FS der eingeschlossenen 70 Zahlen 5016-813 = 4203 = 9*467. Die Zahlen 2, 3 und 4 beziehen sich im Hexagramm auf die radialen Maßeinheiten des Hexagons, der Tetraktys und des DR-Durchmessers.

Die Primzahl 467 gibt 4+6 Tetraktyspunkte und 7 Punkte des Hexagons wieder:

Die 4 Punkte bestehen aus den Eckpunkten und dem Mittelpunkt, die 6 Punkte aus den Kreislinienpunkten.

2. Die ZW/FW-Verrechnung der beiden Teilsummen mit der Gesamtsumme führt zu folgenden beachtenswerten Ergebnissen:

			sm	FW	sm	FW
ZS+FS	813	4203	5016	39
FW	274	473	747	89
sm			5763	128	5891	180
FW			133	14	147	17
5891 = 43*137						197

Die Palindromzahl 747 = 9*83 weist besonders auf die Struktur der Doppelraute hin: Zu den 7 Elementen des hexagonalen Dreiecks kommen durch die hexagonale Erweiterung 4 Elemente hinzu. Wenn die untere mit der oberen Spitze verbunden wird, ergibt sich – vom Mittelpunkt aus gesehen – die Zahlenfolge 74(4)7. Die 11 Elemente der Raute bestehen aus 4+4 Rahmenelementen und 3 Binnenelementen:

Die Zahl 197 ist mit 133 auf zweifache Weise verwandt:

Erstens, 133 besteht aus den Faktoren 19*7. Zweitens, teilt man 197 in die zweistelligen Primzahlen 19+17+97 auf, ist das Ergebnis wiederum 133.

Die Faktoren 19*7 stehen auf folgende Weise mit der Punktestruktur 1-3-3 der DR in Beziehung: 5 hexagonale Punkte + 7 DR-Punkte geben die Kreisflächengrößen 1+3 wieder, 5 hexagonale Punkte + 2 Erweiterungspunkte die Kreisflächengrößen 1+2. Aus der Addition der Punktezahl ergibt sich 12+7 = 19, aus den Flächengrößen 4+3 = 7:

VI. Drei Zahlenebenen

a) Die Stufen 2 und 1

1. Bei konzentrischer Betrachtungsweise der drei Zahlenreihen fällt die mittlere (44-60) nach 9 Schritten und die zweite (62-83) nach 11 Schritten weg. Es bleiben noch 10 Schritte der ersten Reihe (1-42) übrig. Es ergibt sich so die Folge 9-2-10 sowie 3-2-1 als stufenweise Abnahme der beteiligten Zahlenreihen. Zu den 9 Grundzahlen, die als Punkte 8 Maßeinheiten begrenzen, müssen noch 2 Punkte hinzukommen, damit 10 Maßeinheiten aufgefüllt sind:

Als vierstellige Zahl hat 9210 den FW 317. Die Zahlen 3+17 stellen, wie oben ausgeführt, das Kreismodell als Pendant zum Streckenmodell dar.

2. Die erste Stufe umfaßt 9*6-1 = 53 Zahlen, die zweite 2*4 = 8 Zahlen, die dritte 10*2 = 20 Zahlen.

3. Das konzentrische Fortschreiten kann von der Mitte und vom Rand aus erfolgen. Es verändern sich dabei nur die FS. Von besonderem Interesse sind die Ergebnisse der 2. und 1. Stufe.

4. Die ZS+FS von der Mitte aus:

St.2	1-42				sm	62-83				sm	GS
Zahl	12	11	31	32	86	63	62	82	83	290	376
FW	7	11	31	10	59	13	33	43	83	172	231
					145					462	607

St.1	10-1	33-42	sm
ZS	55	375	430
FS	46	193	239
			669

607+669 = 1276 = 4*11*29 > FW 44

5. Die ZS+FS von den Rändern aus:

St.2	1-42				sm	62-83				sm	GS
Zahl	10	11	32	33	86	71	72	73	74	290	376
FW	7	11	10	14	42	71	12	73	39	195	237
					128					485	613

St.1	12-21	22-31	sm
ZS	165	265	430
FS	108	160	268
	273	425	698

613+698 = 1311 = 3*19*23 > FW 45

6. Die zwei Summen 1276 und 1311 tragen zweimal der Gleichung 1+2 = 3 Rechnung. Denn die Gesamt-ZS+FS 5016 ist sowohl durch 11 als auch durch 19 teilbar. Die beiden ZS+FS der 3. Stufe sind 3740 = 20*11*17 > FW 37 und 3705 = 3*5*13*19 > FW 40.

7. Die ZS und FS der Stufen 2 und 1 erweisen mehrfach ihre trinitarische Bedeutung der Zahlen 1 und 3:

St.	2	1	sm
ZS	376	430	806
FS	53	50	103
			909
806 = 21331

Das Produkt 13*31 = 403 ist der Durchschnittswert für 14 Zahlen. Die Primzahl 103 bezieht sich vornehmlich auf 10 Tetraktyspunkte und die verbleibenden 3 Eckpunkte des Hexagramms.

Auch die FS sind durch 13 teilbar und bilden sogar paarweise ein bemerkenswertes Verhältnis. Zu addieren sind jeweils die FS einer Stufe:

St.	2	1	sm
Mitte	231	239	470
Rand	237	268	505
	468	507	975
Diff.	6	29	35
468:507 = *313(12:13)*

Die Einzelziffern sowohl der gemeinsamen Faktoren 3*13 als auch der Verhältniszahlen 12:13 geben die beiden Kreisflächenverhältnisse des Tetraktyssterns wieder. Die Differenzbeträge 6 und 29 setzen sich komplementär aus den ZS 1+2 und 9+8 sowie ihren FW zusammen:

Zahl	1	2	3	9	8	17
FW	1	2	3	6	6	12
			6			29

8. Auch die addierten FW der FS einer jeden Stufe enthalten die Zahlen 1 und 3:

St.	2		sm	1
FS	231	237		239	268
FW	21	82	103	239	71	310

Die addierten FW der 4 ZS und 4 FS betragen demnach 103+103+103+310 = 309+310 = PZ 619. Die Addition der ZS+FS und ihrer FW beträgt 5174+619 = 5793 = 3*1931. Die Primzahl 1931 ist eine Zusammensetzung aus den Zahlen 12 und 21 sowie der Addition ihrer FW 7 und 10.

Anmerkenswert ist die Verrechnung der FS und der Summe ihrer FW:

	FS	S-FW	sm	FW
	975	413	1388	351
FW	26	66	92	27
sm				378
351 = 2713; 378 = 2714
1388 = 4*347

351 und 378 sind die Summen der Zahlen 1-26 und 1-27. Die Zahlen 26 und 27 sind beziehbar auf die 26 und 26+1 Elemente des Oktaeders, wobei 1 das Volumen bezeichnet. Die Primzahl 347 ist die trinitarische Zahl schlechthin.

9. Das FS:ZS-Verhältnis der beiden ersten Stufen beträgt 975:1612 = 13*(75:124) = 13*199 = 2587. Die Zahl 13 wird man den 13 Punkten des Hexagramms zuweisen, die Primzahl 199 der Tetraktys. Es zeigt sich dabei eine Doppelbedeutung:

In der ersten Bedeutung bezeichnen drei Einzelziffern den Mittelpunkt und je 9 Punkte und 9 Linien der drei Tetraktysseiten, in der zweiten Bedeutung werden die ersten beiden Ziffern zusammengefaßt und es kommen noch 9 Dreiecke hinzu. Beide Additionen geben das oben gezeigte Kreismodell des Dezimalsystems wieder.

199 ist auch Faktor der zweimal zwei FS der Stufen 1+2 und 3:

	Mitte		Rand
St.	1+2	3	1+2	3
FS	470	1164	505	1129	3268
FW	54	104	106	1129	1393
1393 = 7*199					4661

10. Die ZS der 3. Stufe beträgt 2576 = 16*7*23 > FW 38. Der Bezug zu den Flächenverhältnissen der beiden Tetraktyskreise ist auf mehrfache Weise zu erkennen. Die Einzelziffern des Produktzahlen 16*7 = 112 weisen auf zweimal 7 Punkte des Hexagramms hin, wobei der Mittelpunkt zweimal zu zählen ist. Den Einzelziffern von 112 entspricht das Kreisflächenverhältnis 1:3:

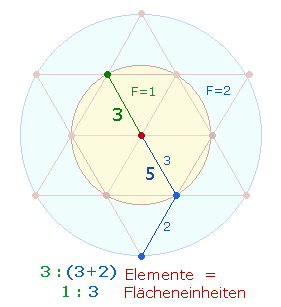
Die Zahl 23 setzt sich zusammen aus 5+4 und 5+9 Durchmesserlementen der DR und gibt die Flächenverhältnisse 1:2 und 1:3 wieder. In der Addition sind dies 7 Flächeneinheiten.

Die Zahl 16 ist als 8+8 Radialelemente der DR, indem zweimal 3:5 Elemente das Flächenverhältnis 1:3 wiedergibt:

Erstellt: August 2014

INHALT 2