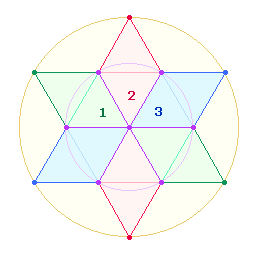
Die trinitarische Gleichung 1+2=3
Mathematisch-theologische
Reflexionen
A. Trinitarische
Entfaltungen
I.
Erste Überlegungen
II.
Ein Gott oder drei göttliche Personen
IV.
Der Kreis
V.
Doppelkreis und Tetraktysstern
B. Die drei
göttlichen Personen in Hexagon und Tetraktysstern
C. Was bedeutet eigentlich 1 Gott
in 3 Personen?
I. Erste
Überlegungen
1.
Ausgangspunkt trinitarischen Zahlendenkens ist die Gleichung 1+2=3. Sie ist die niedrigste aller
additiven Gleichungen mit der niedrigsten Zahl von 2 Additoren. Einerseits ist sie das
Grundmuster aller additiven Gleichungen, andererseits besitzt sie einmalige
Eigenschaften:
2.
Das Ergebnis 3 ist nur einmalig zusammensetzbar, während höhere Summen
verschieden zustande kommen können: 2+4 = 6, 1+5 = 6; 1+2+3 =
6.
Die Addition der
ersten beiden aufeinanderfolgenden Zahlen ergibt die auf die zweite folgende
Zahl 3. Alle anderen Additionen von zwei
sukzessiven Zahlen führen zu einem Ergebnis, das eine oder mehr Zahlen
Zwischenraum zur zweiten Additionszahl bewirkt: 2+3 = 5, 8+9 = 17.
3.
Auf der Ebene der Ordinalzahlen kann man zwar nicht sagen
"Der Erste und der Zweite ist gleich der Dritte", aber "Die Drei
(=Der Dritte) enthält die Eins und die Zwei in sich." Dies ist auch der
Fall bei höheren Summen, jedoch mit Alternativen: Die Sieben enthält die Drei
und die Vier oder die Zwei und die Fünf.
4.
Die Gleichung 1+2=3 ist also in der Weise
auschließlich und alternativlos, daß nur von ihr gilt: Das Ergebnis 3 besteht aus 1+2, die dritte göttliche Person aus der ersten und der zweiten.
5.
Die Gleichung 1+2 ist nur möglich, wenn das Ergebnis 3 real existiert. Eine additive
Gleichung bedeutet also immer die reale Existenz einer doppelten Anzahl.
6.
Auf die drei göttlichen Personen bezogen, bedeutet dies:
Die zweite Person kann nur existieren, weil die dritte existiert, bzw., die
dritte kann nicht existieren, wenn nicht die zweite existiert. Mit der zweiten
Person ist also die dritte mitgegeben.
II. Ein Gott oder drei göttliche Personen
(Zwischenkapitel)
1.
Christen ist die Vorstellung von drei göttlichen Personen
vertraut, da sie ja durch die Taufe auf Vater, Sohn und Heiligen Geist in eine
kirchliche Gemeinschaft aufgenommen wurden. Wenn ihnen nicht ein sich besonders
fortschrittlich dünkender Theologe, Pfarrer oder Religionslehrer Zweifel in die
Seele gesät hat, halten sie die drei göttlichen Personen für real existierend,
auch wenn sie sich nicht weiter mit ihnen beschäftigen. Ihr allgemeiner
Bewußtseinszustand dürfte sein: Es wird schon stimmen, was das Glaubensbekenntnis
aussagt.
2.
Wie steht es aber mit den Juden und Muslimen, die sich vom Christentum
abgrenzen, indem sie vehement die Dreifaltigkeitslehre ablehnen und in einem
monotheistischen Gott die alleinige Wahrheit sehen. Hier rührt sich in mir das
inzwischen wohlbekannte Thema über das Verhältnis von Glaube und Vernunft. Kann
man mit Vernunft über das Wesen Gottes nachdenken, wenn man sich ihn als einen
einsamen Gott vorstellen muß? Daß Gott außerhalb der Kategorien von Raum und
Zeit steht, ist schwer genug vorstellbar. Aber von Ewigkeit her allein?
Vielleicht gerade noch in Gesellschaft von Engeln, die aber auch durch
Schöpfung einen zeitlichen Anfang haben? Hat etwa Gott die Welt geschaffen,
damit es ihm nicht langweilig würde? Als Beschäftigungstherapie gewissermaßen?
Eine monadische
Vorstellung von Gottes Existenz hat vermutlich zur Folge, daß bestimmte
Gottesfragen gar nicht gestellt werden und so der Mensch letztlich zu wenig
rationale und damit personale Beziehungen zu Gott hat.
3.
Hingegen über die Beziehungen der drei göttlichen Personen
zu einander, zur Schöpfung und zum Menschen nachzudenken, haben die größten
christlichen Denker unendlich viel Mühe und Zeit aufgewendet. Tatsächlich
bieten die Evangelien dazu genügend Anhaltspunkte. Solche Bemühungen dienen
nicht nur dem Fortschritt und der Klärung wissenschaftlich-rationalen Denkens,
sondern dem höchsten Ziel menschlichen Daseins, Gott zu lieben und ihn
anzubeten.
Bevor ich mich meiner eigentlichen
Aufgabe wieder zuwende, möchte ich zur trinitarischen Realität lediglich
beitragen, daß die erste göttliche Person der Ursprung der beiden anderen ist,
daß also aus der ersten Person die Logik der trinitarischen Beziehungen
hervorgeht. In dieser Hinsicht bedeutet die christliche Dreifaltigkeit nicht
nur per definitionem ein Gott in
drei Personen (= Einheit der drei Personen), sondern eine Gemeinschaft von drei
Personen aus dem Ursprung des einzigen Gottes, eben der ersten Person.
1. Ein Kunstwerk ist,
so lautet eine Definition, "unmittelbarster Ausdruck der individuellen
Persönlichkeit des Künstlers" (IQ). Ein Künstler kann also gar nicht
anders als aus seinem inneren Selbstverständnis zu arbeiten. Es besteht also
eine Identität zwischen Künstler und Kunstwerk.
2. Auch Gott kann
(sozusagen) nicht anders, als nach seinem Selbstverständnis die materielle Welt
hervorzubringen. Dieses Selbstverständnis gründet im unendlichen Beziehungsreichtum
der drei göttlichen Personen untereinander. Umgekehrt müßte man sagen, der
einsame Gott der Juden und der Muslime wäre gar nicht fähig, die Welt zu
schaffen, weil die Gleichung 1+2=3 in seinem Selbstverständnis gar nicht vorhanden ist. Er
hätte einfach keinen Bezug zur Zahl.
3. Glücklicherweise
haben wir es nicht mit einem einsamen Gott zu tun. Aus dem Reichtum der
trinitarischen Beziehungen gehen alle apriorischen Ideen hervor. Dazu gehören
besonders alle geometrischen und räumlichen Figuren.
1.
Der Kreis mit seiner anfangs- und endelosen
Umfassungslinie symbolisiert Unendlichkeit Gottes am sinnfälligsten. Es zeigt
sich, daß mit der Zwei
des Kreisbogens auch die Drei der Fläche untrennbar gegeben ist.
2.
Der Kreis besteht also aus den drei Elementen Mittelpunkt, Umfassungslinie und Fläche. Nun bedeutet, wie oben
dargelegt, eine additive Gleichung die doppelte Anzahl von Existierendem. Zu den ersten
3 Elementen brauchen wir also nochmals 3 Elemente. Dies wird wohl ein zweiter Kreis
sein, der nur in einer konzentrischen Anordnung dem Anspruch der vollkommenen Beziehung genügt. Der Radius
dieses konzentrischen Kreises muß jedoch aus dem ersten Kreis hervorgehen. Dies
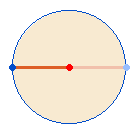
geschieht durch eine erste Unterteilung des Ausgangskreises in zwei Hälften:
|
|
Der Kreis hat zwei
Radien, bestehend aus jeweils 3 Elementen, die damit der Gleichung 1+2=3 genügen. Allerdings besteht der zweimalige
Mittelpunkt nur in der Vorstellung. In Wirklichkeit ist nur einer abgebildet.
Die gesamte Linie nennt man Durchmesser (DM), der aus 5 Elementen besteht.
Trinitarisch bedeutet der Durchmesser, daß die
erste Person nur einmal, die zweite und dritte Person je zweimal dargestellt ist.
Will man nun eine Vermittlung
zwischen den 3 Radialelementen und den 5 DM-Elementen herstellen, kann man
die beiden Punkte, die die erste und zweite Person darstellen, zur Zahl 2 zusammenfassen und der Linie (=
dritte Person) die Zahl 1 geben. Nun läßt sich folgendes Verhältnis zwischen Radius
und Durchmesser formulieren:
2:1 = 3:2
Gibt man dem Mittelpunkt die Zahl 1, dem Kreislinienpunkt die Zahl 2 und der Radiallinie die Zahl 3, genügt das festgelegte Verhältnis 2:1 der Gleichung 1+2=3.
3.
Der einzelne Durchmesser fordert eine trinitarische
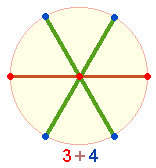
Erweiterung, und zwar von 1 auf 3, da wiederum beide weiteren Durchmesser
untrennbar miteinander verbunden sind:
|
|
Die 3 Hexagonachsen zeigen erstmals die
bedeutsamen Zahlen 3 und 4 in der Verteilung der Punkte.
Die Gleichung 1+2=3 ist nicht mehr in den Punkten und
Linien zu erkennen. Zählt man den Mittelpunkt jeder Achse, erhält man 3+(3+3) Punkte. Die Addition 3+6 verbindet die Ordinalzahlen 1+1+1 und die Kardinalzahlen 1+2+3. Die Linien ergeben zwar 6, aber in der Addition 2+2+2, welche die Gleichheit der drei
göttlichen Personen einführt.
Die Gleichung 1+2=3 zeigt sich neu in 2*3 Teilflächen (durch die
Mittellinie in zwei Hälften geteilt), wobei die mittlere Fläche die Verbindung
zwischen der linken und der rechten darstellt.
4.
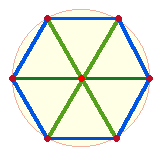
Durch Hinzufügung von 6 Segmentlinien werden aus den
Sektoren gleichseitige Dreiecke:
|
|
Ein gleichseitiges
Dreieck betont die Gleichheit der Personen und genügt der Gleichung 1+2 P = 1+2 L. Hinzu kommt die Fläche als
einigendes 7.
Element, worin erstmalig das Prinzip ein Gott in drei Personen deutlich wird.
Es wird zum 10. Element, wenn die Elemente jeder Seite als 2P+1L gezählt werden.
1.
Das Hexagon besteht nach seiner Vollendung aus 25 Elementen, die einander
verschieden zugeordnet werden können und zwar als:
–
7 Punkte + 6 Flächen = 13 Elemente sowie 2*6 Linien = 12 Elemente,
–
7 Punkte + 6 Radiallinien sowie 6 Segmentlinien und 6
Dreiecksflächen.
Läßt man den
Mittelpunkt als der ursprünglichen Kreiskonstruktion zugehörig unberücksichtig,
erhält man 3*4 (Punkte+Linien) =
12 Elemente
sowie 6 Segmentlinien und 6 Dreiecksflächen = 12 Elemente oder zusammengefaßt 4*6 Elemente.
Durch
Hinzufügung der 3
Kreiselemente ergeben sich 3+24 = 27 Elemente. Rechnet man den Mittelpunkt für Kreis und Hexagon,
erhält man die Doppelrechnung 27+28 = 55 = Summe der Zahlen 1-10.
Die Zahl 27 entwickelt sich aus der Addition
+ Multiplikation der Kardinalzahlen und Ordinalzahlen der Zahlen 1-3:
(6+3)+ 6*3 = 9+18 = 27.
Die Zahl 324 ist die Quadratzahl zu 18. Ordnet man jeder Segmentlinie zwei Begrenzungspunkte zu,
erhält man 6*3 = 18.
V. Tetraktysstern und Doppelkreis
1.
Die Gleichung 1+2=3 kann auch als fortscheitende
Zunahme von Elementen verstanden werden und hat dann die Form 1:2:3. Dies ist im Hexagon bereits mit
den Punkten geschehen: Der 1. Punkt war der Mittelpunkt des
Kreises, der 2.
Punkt kam erster Kreislinienpunkt der ersten Radiallinien hinzu, der 3. schließlich ist der zweite Kreislinienpunkt.
Alle drei Punkte sind somit auf der DM-Linie vereint. Die beiden
Punkteerweiterungen haben also einmal das Verhältnis 1:2 und einmal 2:3.
2.
Die Linien hingegen haben im Hexagon erst zwei Phasen durchlaufen,
nämlich die Erweiterung von einer zu zwei Radiallinien im progressiven
Verhältnis 1:2. Es fehlt noch die 3. zusammenhängende Linie. Gefordert
ist also analog zum Mittelpunkt eine Linie in der Mitte und zwei symmetrische
Seitenlinien.
Die Linie gilt als Zeichen der 3.
Person und als einigendes Band zwischen 1. und 2. Person. Sie schafft nun die
Voraussetzung für den zweiten Kreis durch Verlängerung der 6 Segmentlinien nach jeder Seite. Die verlängerten Geraden
erzeugen 6 Schnittpunkte:
|
|
Die 6 Schnittpunkte
sind zusammen mit den neu entstandenen Dreiecken einerseits als Verdoppelung
der Segmentlinienpunkte, andererseits als Extrapolation des Mittelpunktes
verstehbar.
3.
Nun kann ein zweites bedeutendes Verhältnis gebildet
werden, indem die mittlere Linie einer Seitenlänge von 1 auf 3 und die beiden Begrenzungspunkte
von 2 auf 4 erweitert werden:
1:2 = 3:4
Hinsichtlich der Numerierung bedeutet hier 1 wiederum 3 (Linie),
die beiden Punkte jedoch jeweils 2, sodaß das numerierte Ausgangsverhältnis
nicht mehr 3:3 (s.oben), sondern
3:4 lautet.
4.
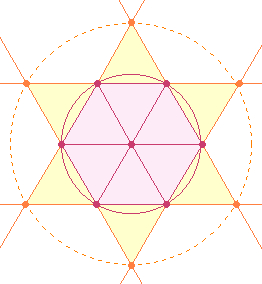
Der Vorgang der Erweiterung des Hexagons ist beendigt,
wenn durch die 6
Schnittpunkte eine Kreislinie gezogen worden ist. Der so entstandene äußere
Kreis hat die dreifache Fläche des inneren Kreises. Das Verhältnis des inneren
zum äußeren Kreis ist demnach 1:3, wenn jedem Kreis ein Mittelpunkt zugestanden wird.
Diesem Flächenverhältnis entsprechen 3:3 = 6 Elemente. Rechnet man nur einen Mittelpunkt, kommt zur
Flächeneinheit 1 der
zwischen den beiden Kreisbogen befindliche Kreisring mit der Flächengröße 2; Das Verhältnis ist 1:2. Diesem Verhältnis entsprechen 2:3 = 5 Kreiselemente. Diese beiden trinitarischen
Verhältnisse, ihre
addierten Formen 4+3/3+4, 7 und als zweistellige Zahlen 13/31, 12/21, 43/34 bilden wiederkehrende
Grundelemente des Dezimalsystems.
5.
Die Erweiterung des Hexagons zum Doppelkreis führt
parallel zum Hexagon selbst zu weiteren 4*6 = 24
Elementen, denen die 3
Kreiselemente hinzugefügt werden können, sodaß sich eine Parallelität von 27+27 = 54 Elementen ergibt. Auf diese
Rechnung hauptsächlich führe ich die überlieferte Zahl von 27 Knaben und 27 Mädchen zurück, die anläßlich der
römischen Säkularfeiern im Jahr 17 v.Chr. in zwei Chören auftraten.
6.
Ohne Kreiselemente und mit einem Mittelpunkt besteht der Tetraktysstern aus 1+(24+24) = 49 Elementen. In ihm kann man 2 Tetraktys mit jeweils 37 und 3 Doppelrauten mit jeweils 21 Elementen erkennen:
|
|
Die Summe der
Elemente dieser 1+2+3 = 6
Figuren = 49+74+63 = 186 = 6*31. Jeder der 6 Figuren kommt also die durchschnittliche Zahl von 31 Elementen zu, wiederum Hinweis auf
das trinitarische Flächenverhältnis der beiden Kreise.
Auch diese Addition
der ersten drei Zahlen genügt der Gleichung 1+2=3. Jede der 3 göttlichen Personen kommt also
die Zahl 62
zu, die zusammen mit der Zahl 61
die Zahl 123
konstituiert. Tatsächlich ergeben die Figuren 1+2 49+74 = 123 Elemente.
Erstellt: Januar 2007