169 Primzahlen von 1-1000 in 6 konzentrischen Quadraten

13*13 Primzahlen von links nach rechts

a) Einleitung

Die Ordnungen der 169 Primzahlen von 1-1000 in 6 konzentrischen Quadraten wecken das Interesse, ob Zahlenbeziehungen auch in iner Anordnung von jeweils 13 Primzahlen je Zeile erkennbar sind. Ich beschränke mich auf zwei Ergebnisse, die mir besonders bedeutsam erscheinen:

1	2	3	5	7	11	13	17	19	23	29	31	37	198
41	43	47	53	59	61	67	71	73	79	83	89	97	863
101	103	107	109	113	127	131	137	139	149	151	157	163	1687
167	173	179	181	191	193	197	199	211	223	227	229	233	2603
239	241	251	257	263	269	271	277	281	283	293	307	311	3543
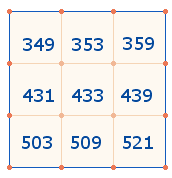
313	317	331	337	347	349	353	359	367	373	379	383	389	4597
397	401	409	419	421	431	433	439	443	449	457	461	463	5623
467	479	487	491	499	503	509	521	523	541	547	557	563	6687
569	571	577	587	593	599	601	607	613	617	619	631	641	7825
643	647	653	659	661	673	677	683	691	701	709	719	727	8843
733	739	743	751	757	761	769	773	787	797	809	811	821	10051
823	827	829	839	853	857	859	863	877	881	883	887	907	11185
911	919	929	937	941	947	953	967	971	977	983	991	997	12423
5405	5462	5545	5625	5705	5781	5833	5913	5995	6093	6169	6253	6349	76128

Die Gesamtsumme der 169 Primzahlen beträgt 76128 = 2⁵*3*13*61 = 96*13*61 = Faktorenwert (FW) 87, sie ist durch 2 teilbar wegen der Primzahl 2, so daß 168+1 Zahlen zu rechnen sind, zwei ungerade Zahlen ergeben immer eine gerade Summe.

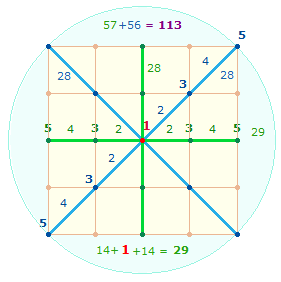
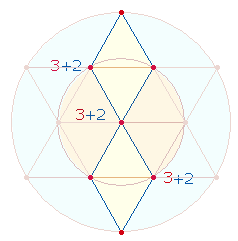
Für die horizontalen und vertikalen Summen habe ich keine Zahlenverhältnisse nach symmetrischen Gesichtspunkten gefunden. Bemerkenswert jedoch sind die Summen der zweimal 12 diagonalen Zahlen (ohne 433) 5472 (1-997) und 5376 (37-911), ihr Verhältnis ist 96*(57:56) = 96*113. Bei der Numerierung der vier Achsen eines Quadrats Q3 von 1-5 ab Mittelpunkt 1 erhält man die Summe 57+56 = 113:

Erstaunlich ist auch die Summe 2379 der vier Eckzahlen und der Mittelpunktszahl 433, sie besteht aus den Faktoren 3*13*61 des Gesamtergebnisses, d.h., die Summe der übrigen 164 Zahlen ist 32*2379.

b) 9 Zahlen des inneren Quadrats

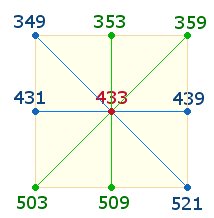
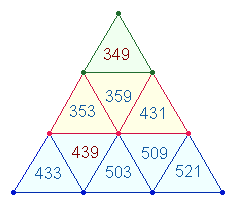
1. Das auffallendste Ergebnis sind die 8 Primzahlen des inneren Quadratrahmens, die das Achtfache der Mittelpunktszahl 433 betragen:

Primzahlen 1-1000 in 13 Zeilen: inneres Quadrat

Die Summen von 2x2 gegenüberstehenden Zahlenpaaren auf den Mittelachsen und den Diagonalachsen betragen jeweils 870+862 = 1732 = 4*433.

Die Einzelziffern der Zahl 433 haben mehrere Bedeutungen:

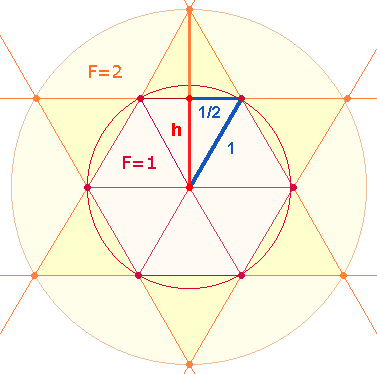
· Die Fläche eines gleichseitigen Dreiecks beträgt 1/4√3 = 0,1732/4 = 0,433. Läßt man die Kommastellen außer Acht, steht 433 für ein gleichseitiges Dreieck. Der Radius des äußeren Tetraktyskreises beträgt √3:

Modell: ein Gott in drei Personen

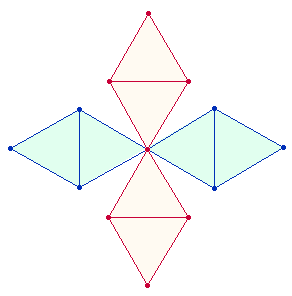
Zweimal 1732 steht für jeweils 4 Dreiecke zweier Doppelrauten, die als Achsenkreuz zu einem Oktaeder zusammengefügt werden können:

9 gleichseitige Dreiecke befinden sich in der Tetraktys:

· Eine Skala von 10 Punkten begrenzt 3*3 Maßeinheiten:

· Die 10 Punkte der Tetraktys lassen sich aufteilen in 4 hexagonale gegenüberstehende Kreislinienpunkte, 3 hexagonale Durchmesserpunkte und 3 Eckpunkte:

· Das (gleichseitige) Dreieck selbst kann die Zahl 10 repräsentieren, wenn man für jede Seite eine Linie und zwei Begrenzungspunkte zählt und die Fläche als Einheit hinzufügt: 3+3+3+1 = 10.

c) Mittelpunkt + 6 Quadratrahmen

1. Ein Zahlenverhältnis kommt zustande, wenn man die Mittelpunktszahl 433 und die Summen von 6 Quadratrahmen nach ungerader und gerader Stellung addiert:

	MP	QR1	QR2	QR3	QR4	QR5	QR6		Faktoren
unger.	433		6974		14228		22429	44064	96* 3* 3* 3* 17 = 96*459 = FW 39
gerade		3464		10494		18106		32064	962167= 96*334 > FW 182
44064:32064 = 96(459:334) = 96793; 459-334 = 125; 96125 = 12000* >FW 13+15 = 28

Die auffällige Differenzsumme 12000 ist in Verbindung mit der Zahl 1000 zu sehen, deren FW 21 auf die drei Tetraktysseiten hinwies. Die Tetraktys kann erweitert werden zu einem Quadrat, dessen Seiten ebenfalls aus 4 Punkten und 3 Linien besteht, so daß 4*(4+3) = 28 als FW von 12000 ergibt:

Die Ergebnisse sind nun im einzelnen auszuwerten:

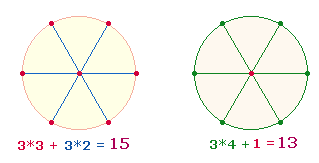
2. Die Zahl 96, gemeinsamer Teiler der beiden Summen, kann mehrere Bedeutungen haben, real oder in Zusammensetzung einstelliger Zahlen:

· Ein Oktaeder setzt sich zusammen entweder aus 4 sanduhrförmigen Doppeldreiecken von je 13 Elementen oder 4 Rauten von je 11 Elementen, aus einer Kombination beider oder aus beiden zusammen. Es ergeben sich so vier Summen: 52, 44; 48; 96.

· Der DR-Rahmen besteht aus 15 Elementen, 9 gehören dem hexagonalen, 6 dem Erweiterungsbereich an:

· Eine DR-Zickzacklinie enthält 5 Durchmesserelemente und zweimal 5 Radialelemente, jeweils 3 Punkte und 2 Linien, in zweistelliger Zusammensetzung ergibt sich 3*32 = 96:

· Die FW von 9+6 sind 6+5 = 15+11 = 26. Dies ergibt eine Beziehung zum Oktaeder, der aus 26 Oberflächenelementen besteht.

· Die FW der beiden Umkehrungen 96 und 69 sind 13+26 = 39 = 3*13. Die Einzelziffern des Produkts geben die Punktestruktur der DR wieder.

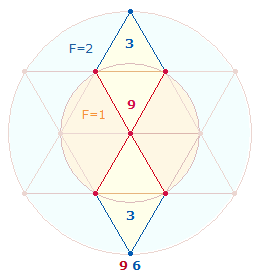
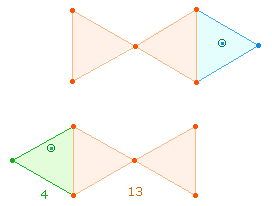
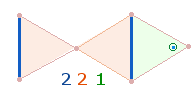
3. Aus dem Produktausdruck 96*125 ergab sich die FW-Zusammensetzung 13+15 = 28. Die beiden FW haben Bezug zu den drei hexagonalen Achsen:

In der ersten Grafik wird für jede Achse ein Mittelpunkt gerechnet, in der zweiten nur einer.

Dieser hexagonale Doppelaspekt ist auch in den beiden Summenfaktoren 334 (Umkehrzahl zu 433!) und 559 erkennbar. Ihre FW sind 169+26 = 13*(13+2). Die Zahl 2 kann hier als zwei zusätzliche Mittelpunkte gedeutet werden.

4. Fügt man den FW der beiden Summenfaktoren den FW 13 des gemeinsamen Teilers 96 hinzu, ergibt sich das Verhältnis 182:39 = 13*(14:3) = 221 = 13*17. Bei der Erweiterung der 3 hexagonalen Doppeldreiecken zum Tetraktysstern, kommt durch Hinzufügung eines Dreiecks auf beiden Seiten eine "Fischfigur" aus 17 Elementen zustande:

Die Zahl 3 des Klammerausdrucks ist auf die drei Dreiecksflächen der Fischfigur beziehbar. Sie sind religiöses Symbol für die drei göttlichen Personen. Die Einzelziffern der Zahl 221 lassen sich etwa so darstellen:

Die Figur enthält 2 Querlinien – im Hexagon Segmentlinien – und 2+1 Dreiecksfläche. Die Fischfigur vereinigt in sich das sanduhrförmige Doppeldreieck aus 13 und die Raute aus 11 Elementen. Dazu passen die Faktoren 11*13 der Zahl 143.

Die Verrechnung der Teilsummen mit der Gesamtsumme führt wiederum zu einem durch 13 teilbaren Ergebnis:

			sm	FW
ZS	44064	32064	76128	87
FW	189	39	221	30
sm				117
117 = 9*13

Die Faktoren 9*13 weisen wiederum auf die beiden zwei- und dreiachsigen Figuren hin, die 4+6 = 10 Maßeinheiten enthalten. Die Einzelziffern geben auch die 13 Punkte des Tetraktyssterns wieder: 9 Punkte eines Tetraktysrahmens, den Mittelpunkt + 3 weitere Eckpunkte der Erweiterung.

Erstellt: Oktober 2018, 2024

Inhalt II