Das Prinzip 1:3 in numerierten Quadraten
a) Einleitung
b) Das Quadrat Qu5
d) Die Zahl 59
f) Die 4
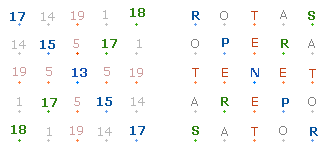
Achsen des SATOR-Quadrats
g) 13 und 12
a) Einleitung
1. Der eine Gott in drei Personen manifestiert sich in der Zahlenordnung des Dezimalsystems. Das Zahlensystem besitzt eine geschlossene und offene Form. Die geschlossene Form ist hauptsächlich das Hexagramm mit zwei konzentrischen Kreisen sowie der daraus hervorgehende Oktaeder. Die offene Form besteht in der Punktenumerierung sich endlos erweiternder konzentrischer QUADRATE. Die geschlossene Form ist der Bezugspunkt aller sich ausdehnenden Zahlen, wie sich an dem ausgewählten Beispiel zeigen läßt. Mittel hierzu sind die Faktorenwerte (FW) der Zahlen.
2. Über die Gesetzmäßigkeiten von Erweiterungen habe ich bereits einen Beitrag verfaßt, auf den ich verweise. Hier geht es besonders um den Nachweis des Prinzips 1:3, das sich besonders in den Umkehrzahlen 13 und 31 zeigt, weiterhin in Analogien, die das Hexagramm und seine beiden konzentrischen Kreise bieten. Es ist zu erwarten, daß das erste Erweiterungsquadrat exemplarisch das trinitarische Prinzip 1:3 enthält.
b) Das Quadrat Qu5
|
|
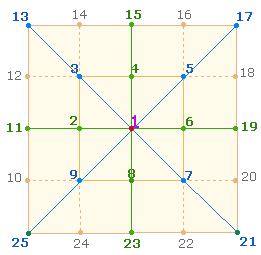
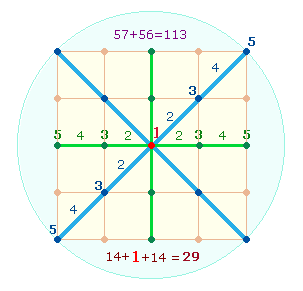
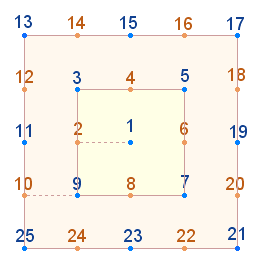
1. Die Numerierung des Ausgangsquadrats erfolgt vom Mittelpunkt aus, hier nach links und im Uhrzeigersinn. Die Position der Zahl 2 auf dem horizontal-vertikalen Achsenkreuz ist sinnvoll, da Achsenkreuze die Grundlage von Quadraten bilden.
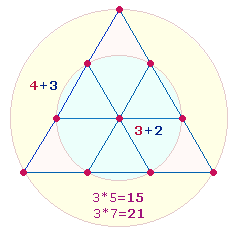
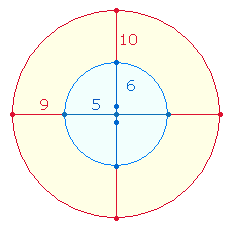
Das erste Quadrat besteht aus dem Mittelpunkt und 8 Rahmenzahlen und endet mit 9, dem Quadrat von 3, der zweite Quadratrahmen besteht aus 8+8 Punkten endet mit 25, dem Quadrat von 5. Auch jeder weitere Quadratrahmen endet mit einer Quadratzahl. Die zu quadrierende Zahl bestimmt sich nach der Zahl der Punkte (P) und Linien vom Mittelpunkt, praktischer Weise nach der Formel 2P-1.
Die Zahl 10 als Abschluß der ersten Zehnereinheit gehört zum zweiten Quadratrahmen und übt damit gleichsam eine dynamische Funktion aus, die sich in jeden neuen Quadratrahmen hinein fortsetzt.
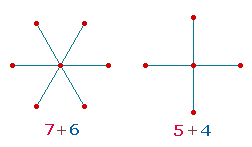
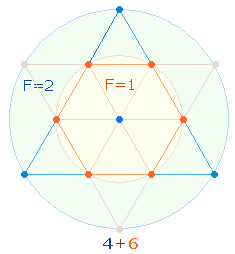
2. Das Prinzip 1 zu 3 besteht darin, daß von den vier Eckpunkten eines Quadrats jeweils drei Zahlen zum nächsten Quadratrahmen führen, diagonal, horizontal und vertikal. Die horizontalen und vertikalen Punkte kommen an dieser Stelle jeweils neu hinzu.
Um
die trinitarische Ordnung dieser Gesetzmäßigkeit zu erkennen, ist die
Einbeziehung der Faktorenwerte (FW) unverzichtbar. Weitere Auskunft erhält man,
wenn man auch die FW der Zahlensummen (ZS) und Faktorensummen (FS)
hinzunimmt.
Zunächst sollen die 4*3 neuen Zahlen untersucht werden. Der ZS und FS sind ihre FW unmittelbar nachgestellt:
|
ZS |
FW |
sm |
FS |
FW |
sm |
GS |
|
212 |
57 |
269 |
120 |
14 |
134 |
403 |
|
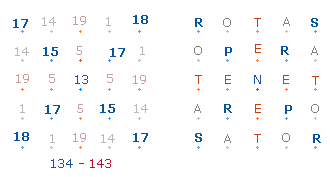
212
= 4*53; 403 = 13*31 |
||||||
Die Einzelziffern der Gesamtsumme 403 weisen auf 4*3 neue Zahlen, das Produkt der Umkehrzahlen 13*31 auf das Prinzip 1:3 hin.
Die Einzelziffern der Summe 134 kennzeichnen den Vorgang der quadratischen Erweiterung in dem Ausdruck (1+3)*4. Sie erfüllen weiterhin die Gleichung 1+3 = 4. Geometrischer Bezugspunkt dieses gleichbleibenden Vorgangs unendlicher Erweiterungen ist die Punktestruktur der Doppelraute (DR) im Hexagramm, wenn deren Mittelpunkt zweimal gezählt wird:
|
|
Die Summe 134 gibt den ersten Hinweis darauf, daß die Ergebnisse aller sich erweiternden Quadrate auf die Eigenschaften des Hexagramms und des Oktaeders zurückgebunden sind.
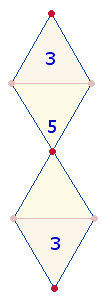
Je drei Zahlen einer Quadratecke haben die durchschnittliche ZS 53. Die Die Einzelziffern 5 und 3 weisen sowohl auf das geschlossene Hexagramm als auch auf das für Erweiterungen offene Quadrat hin:
· Die
Einzelziffern 5 und 3
sind viermal als Radialelemente der zwei
Zickzacklinien der DR interpretierbar:
|
|
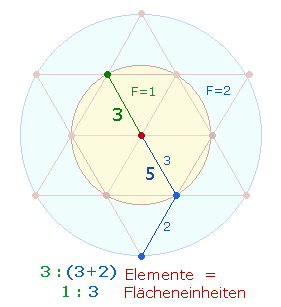
Die Fläche des äußeren Kreises
beträgt das Dreifache des inneren
hexagonalen Kreises. 5:3 Radialelemente
bedeuten daher das Flächenverhältnis 3:1.
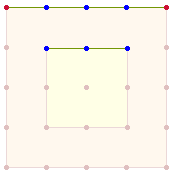
· Den
5:3 Radialelementen (Punkte und Linien) der zwei
konzentrischen Tetraktyskreise entsprechen 5:3 Punkte der vier äußeren und inneren Quadratseiten:
|
|
Die FS 120 bedeutet den FW 10 als durchschnittlichen Wert der 12 Zahlen und 30 für je drei Zahlen.
Die Einzelziffern der ZS 212 sind als Durchmesserlemente des Hexagons oder 5 Durchmesserpunkte der DR zu verstehen.
3. Wenn man die 4 Eckpunkte des Ausgangsquadrates hinzunimmt, ergeben sich folgender Werte:
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
236 |
141 |
377 |
63 |
50 |
113 |
490 |
|
377 = 13*29 = FW 42; 141 = 3*47 |
||||||
|
236
= 4*59 |
||||||
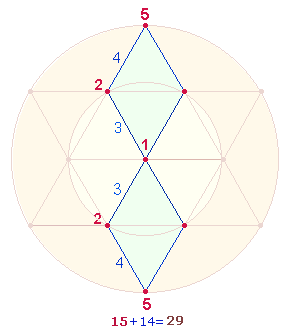
Die Einzelziffern des Faktors 59 geben 5:9 Durchmesserelemente der DR und 5:9 Seitenelemente des Qu5 wieder, wenn man zu den 3 und 5 Punkten jeweils 2 und 3 Linien (s.Grafik) hinzufügt.
5:3 Radialelementen und 5:9 Durchmesserelementen der beiden Tetraktyskreise entsprechen die umgekehrten Kreisflächenverhältnisse 3:1 und 1:3.
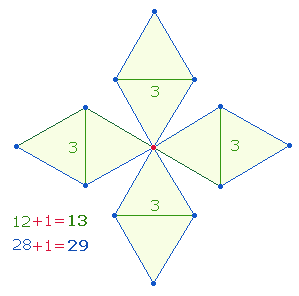
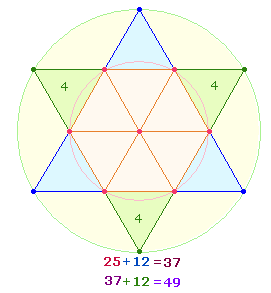
Die ZS+FS 377 ohne Mittelpunkt ist durch 13 teilbar und entspricht so dem trinitarischen Muster 1:3. Das Produkt 13*29 ist auf ein DR-Kreuz beziehbar:
|
|
13 bezieht sich auf 12 Binnenelemente + Mittelpunkt, 29 auf 28 Rahmenelemente + Mittelpunkt. Da eine DR aus 21 Elementen besteht, wird durch zwei Mittelpunkte die volle Zahl von 42 Elementen zweier DR gewahrt.
Der FW 42 ist auch auf je 3 Seiten zweier Tetraktys anwendbar, von denen jede aus 7 Elementen besteht. (Die folgende Grafik zeigt eine einzelne Tetraktys):
|
|
Die Einzelziffern der Zahl 377 sind als 3+7 Tetraktyspunkte und 7 Hexagonpunkte verstehbar, sie repräsentieren das Kreisflächenverhältnis 1:3 der beiden konzentrischen Kreise.
1. Es gibt mehrere strukturelle Aspekte, die untersucht werden können. Einer davon ist, die Eckpunkte und die Punkte (P) davor und danach getrennt zu addieren, also 4 Zahlen für jede Position:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
FW |
|
li.P |
72 |
33 |
105 |
12 |
14 |
26 |
131 |
131 |
|
EP |
76 |
50 |
126 |
23 |
12 |
35 |
161 |
30 |
|
re.P |
64 |
37 |
101 |
12 |
37 |
49 |
150 |
15 |
|
|
212 |
120 |
332 |
47 |
63 |
110 |
442 |
176 |
|
442
= 2*13*17; 442+176 = 618 =
6*103=3*206 |
||||||||
|
105:126
= 21*(5:6); 105+101 = 206 |
||||||||
Wenn es um die Bestimmung der drei göttlichen Personen geht, würde man die linken Punkte der zweiten Person, die Eckpunkte der dritten Person und die rechten Punkte der ersten Person zuordnen. Die Ergebnisse sind in mehrfacher Hinsicht bemerkenswert:
·
Die FS der ersten
und zweiten Person bilden komplementär zur dritten Person das Verhältnis (37+33):50 = 10*(7:5).
· Der
ZS+FS 101
der ersten Person entspricht die ZS 55 + FS 46 der Zahlen 1-10.
Die Einzelziffern von 64 und
37 ergänzen sich jeweils
zur Summe 10 und sind auf die Punkte von
zwei Tetraktys beziehbar. Die FW-Summe 49 bezeichnet die Zahl der
Hexagrammelemente: 37 Elemente einer
Tetraktys und die restlichen 12, die mit den
25 Elementen des Hexagons die zweite
Tetraktys bilden:
|
|
· Die
Summen 126 und 35
der dritten Person sind durch 7 teilbar und bilden das Verhältnis 7*(18:5). In einer numerierten
Tetraktys beträgt die Summe der Eckpunkte 18 und die Mittelpunktszahl ist 5.
Die zweite und erste Person enthalten die durch 7 teilbaren Summen 105+49 = 154, sie
bilden mit der Summe 161 das Verhältnis 7*(22:23) = 7*45 = 315. Die restliche Summe 127 ist eine Primzahl und als die Zahl 12 + der FW 7
sowie als 1+2+7 Punkte der Tetraktys
interpretierbar. 12+7 DR-Punkte geben 4+3 Flächeneinheiten wieder, in
Übereinstimmung mit 3+1+3 DR-Punkten.
· Eine
weitere Komplementarität ergibt sich durch 105+101
= 206 =
2*103. Die Zahl 103, aufgeteilt in 10+3, weist auf 10 Tetraktyspunkte +
3 übrige Punkte des Hexagramms hin. 206,
aufgeteilt in 20+6, gibt die 26 Elemente des Oktaeders wieder. Die Summe 442+176 = 618 weist jeder der drei Personen den
Durchschnittswert 206 zu.
·
Die Faktoren 2*13*17
= FW 32 der ZS+FS 442
sind auf den Oktaeder beziehbar: Aus 26 = 2*13
Elementen besteht die Oberfläche des Oktaeders, aus 2*17
Elementen zwei Oktaederhälften, indem die 8
Elemente der gemeinsamen Mittelbasis zweimal gezählt werden.
Dem FW 32 entsprechen 4 Bahnen des Oktaeders zu je 8 Elementen.
Die Einzelziffern der Summe 442 sind zunächst in der DR als 8 Rahmen- und 2 Querlinien der DR enthalten, sie lassen sich aber auch auf 8 Elemente des Oktaeders und 2 entgegengesetzte Ecken beziehen.
·
Die 26 Elemente des Oktaeders sind in den FW 12 und 14
der zweiten Person erkennbar: 12 Kanten und 6 Ecken + 8
Flächen.
2. 1:3 zusammengehörige Punkte 4*4 Zahlen des Quadrats. Von jeder 4-er Gruppe lassen sich die 4Werte ermitteln, sie werden im Uhrzeigersinn angeordnet:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
FW |
|
obr. |
42 |
32 |
74 |
12 |
10 |
22 |
96 |
13 |
|
obl. |
56 |
38 |
94 |
13 |
21 |
34 |
128 |
14 |
|
unr. |
70 |
39 |
109 |
14 |
16 |
30 |
139 |
139 |
|
unl. |
68 |
32 |
100 |
21 |
10 |
31 |
131 |
131 |
|
|
236 |
141 |
377 |
60 |
57 |
117 |
494 |
297 |
|
117:377 = 13*(9:29) = 2*13*19; 494+297 = 791 = 7*113 |
||||||||
|
60:57 = 3*(20:19) = 3*39 |
||||||||
Auch die FW1/2-Summe 117 ist durch 13 teilbar. Das Verhältnis 9:29 ist auf die 9 Elemente der DR beziehbar, die in der Numerierung von 1-5 vom Mittelpunkt aus die Summe 29 ergibt:
|
|
Je zwei ZS+FS sowie je zwei FW1/2-Summen sind durch 29 und 13 teilbar:
|
|
|
sm |
|
FW |
|
|
sm |
|
|
|
74 |
100 |
174 |
6*29 |
34 |
22 |
30 |
52 |
4*13 |
17 |
|
94 |
109 |
203 |
7*29 |
36 |
34 |
31 |
65 |
5*13 |
18 |
|
|
|
|
|
70 |
|
|
|
|
35 |
|
70:35 =
35*(2:1) = 105; 494+105 = 599 |
|||||||||
Die Einzelziffern der Primzahl 599 beziehen sich auf die Durchmesserelemente des Hexagons und des Hexagramms und geben (1+3)+3 Kreisflächeneinheiten wieder:
|
|
Die Gesamtsumm 494, aufgeteilt in 49+4 weist auf die 49 Elemente des Hexagramms sowie auf 2 Kreisbögen + 2 Kreisflächen hin. Die ZS der Kapitolinischen Trias beträgt 494.
1. In einer weiteren Betrachtungsweise sollen die 4Werte der 4*4 den Diagonalen zugeordneten Zahlen und der 9 Zahlen des horizontal-vertikalen Achsenkreuzes ermittelt werden. Letzterem ist der Mittelpunkt zugewiesen:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
di.A. |
236 |
141 |
377 |
63 |
50 |
113 |
490 |
|
h-v.A. |
89 |
79 |
168 |
89 |
79 |
168 |
336 |
|
sm |
325 |
220 |
545 |
152 |
129 |
281 |
826 |
|
236
= 4*59; 490:336 = 14*(35:24) = 14*59 |
|||||||
|
826
= 2*413 |
|||||||
Die Gesamtsumme 826 enthält wie auch die ZS 236 den Faktor 59.
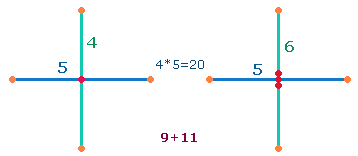
In einem Achsenkreuz, das von der Mitte aus von 1-5 numeriert wird, läßt sich die zweite Achse mit 2 Mittelpunkten versehen, sodaß sich die Summe 29+30 = 59 ergibt:
|
|
Auf die Zahl 29, die Summe einer Achse mit einem Mittelpunkt, weist die die FW1/2-Summe 281 hin, die als 28+1 zu verstehen ist. Aus 29 Elementen besteht, wie schon erwähnt, auch der Rahmen eines DR-Kreuzes. Wenn man sich ein zweites DR-Kreuz mit zwei Mittelpunkten, also 15 Rahmenelemente für jede DR, denkt, erhält man aus 29+30 ebenfalls die Summe 59.
Die Zahl 413 = 7*59 = FW 66 in der Bedeutung 4*(1+3) enthält in den Einzelziffern das Prinzip sich erweiternder Quadrate. 59 ist die Summe der drei Zahlen 24+25+10 im linken unteren Quadrateck. Die doppelte Summe 826 läßt sich auf die Punkte eines DR-Kreuzes beziehen, worin 413 zweimal der Gleichung 4=1+3 entspricht. Der Faktor 7 kann alternativ zur Quersumme 8 (von 413) die 7 Punkte der DR wiedergeben, der FW 66 die 6 Rauten des Hexagramms bedeuten, von denen jede aus 11 Elementen besteht.
Die folgenden Überlegungen gehen von den Einzelziffern 5 und 9 aus.
2. In vorstehendem Achsenkreuz sind nur die Punkte numeriert. Ein Achsenarm besteht aus 5 Punkten und 4 Linien (Maßeinheiten), also aus 9 Elementen. Bei einem Mittelpunkt enthält das Achsenkreuz 17 Punkte und 16 Linien, zusammen 33 Elemente.
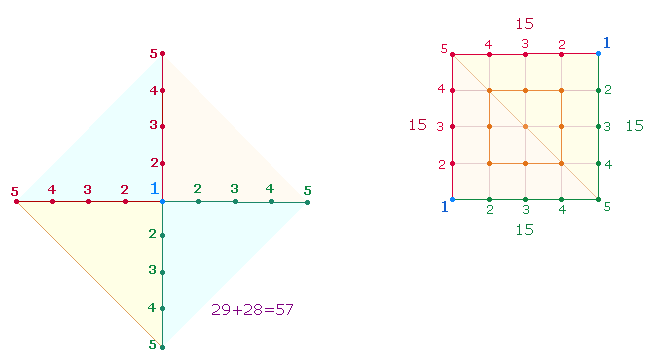
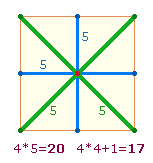
Aus dem Achsenkreuz läßt sich ein Quadrat bilden, wenn man einen Winkel gegen den anderen verschiebt, bis die Endpunkte deckungsleich sind:
|
|
Durch Einziehen von Verbindungslinien erhält man die ersten beiden konzentrischen Quadrate, deren Seiten aus je 3 und 5 Punkten bzw. – unter Einbeziehung der Linien – 5 und 9 Elementen bestehen. Damit stimmt überein, daß die 4*3 numerierten äußeren Punkte 212 = 4*53 und mit den 4 inneren Eckpunkten 236 = 4*59 betragen. Auf Radialelemente und Durchmesserelemente der DR bezogen, bedeuten die Einzelziffern die Kreisflächenverhältnisse 3:1 und 1:3 , wie bereits oben durch die Summe 403 = 31*13 deutlich geworden ist.
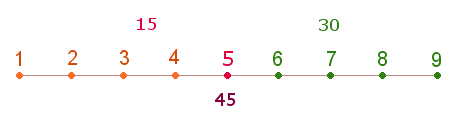
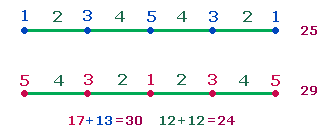
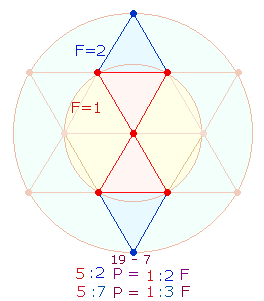
Die 5 und 9 Elemente haben eine Parallele in dem Produkt 5*9, das die Summe der Zahlen von 1-9 bezeichnet. Betrachtet man die beiden Zahlen nicht in ihrer konzentrischen Stellung – wie in zwei konzentrischen Kreisen, sondern numeriert sie linear von 1 ab, ergeben sich zwei Zahlenverhältnisse:
|
|
Das Verhältnis der Summe 15 der Zahlen 1-5 zur Summe 30 der Zahlen 6-9 beträgt 1:2 und zur ganzen Summe 45 1:3. Damit besteht eine genaue Parallele zu den zwei Flächenverhältnissen 1:2 und 1:3 der beiden konzentrischen Kreise des Hexagramms, mit dem Unterschied, daß die Durchmesserelemente konzentrisch liegen und vom Mittelpunkt her definiert sind.
Wie aus einem Achsenkreuz ein Quadrat wird, so läßt sich aus zwei DR des Hexagramms ein Oktaeder zusammenfügen. Jede DR entsteht durch zwei verschränkte Zickzackdurchmesser, jeder geprägt durch das Verhältnis von 5:9 konzentrischen Elementen.
Während das Hexagramm und die beiden konzentrischen Kreise geschlossen sind, können konzentrische Quadrate endlos erweitert werden. Die Parallelität von 5:9 Elementen in beiden Konstruktionen errichtet eine bleibende Ordnungsbeziehung der Gleichung 3+1=4 bzw. (4=3+1) von zwei Rauten, die eine Doppelraute bilden, und dem Produkt 4*(1+3) bzw. (1+3)*4, das für jedes weitere konzentrische Quadrat gilt.
1. Die Ergebnisse der eben ausgeführten ZW/FW-Verrechnung enthalten wesentliche Beziehungen zwischen den Eigenschaften des Hexagramms und des Quadrats und sollen im einzelnen erklärt werden.
2. Den Anfang sollen die FS 220 und 561 machen. Sie geben bereits Hinweise auf wichtige Zusammenhänge. 561 = 33*17 ist die Summe der Zahlen von 1-33, also die Zahl der Elemente des oben gezeigten Achsenkreuzes AK5, das durch Winkelverschiebung zu einem Quadrat Qu5 wird. Letzteres besteht aus 25 Punkten. Die FS der Zahlen 1-25 beträgt 220.
Von Bedeutung ist der Klammerausdruck 11*(20:51) = 11*71 = FW 82. Das Ausgangsquadrat Qu3 besteht aus 4 Achsen zu je zu 3 Punkten und 2 Maßeinheiten (Linien). Bei einem Mittelpunkt entfallen 3 Mittelpunkte, sodaß man den Doppelaspekt von 17+3 Elementen erhält:
|
|
Die Addition von 17+3 = 20 und 17*3 = 51 ergibt die Umkehrzahl 71, deren Einzelziffern auf 7 Punkte der DR + 1 zusätzlichen Mittelpunkt bezogen werden können. Der FW 82 gibt zweimal die Elemente von drei geometrische Figuren in der DR wieder, die Einzelziffern 8 Rahmen- und 2 Querlinien der DR:
|
|
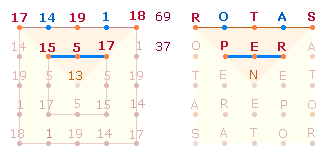
Der Doppelaspekt von 17+20 = 37 Elementen des Qu3 läßt sich für das zweite konzentrische Quadrat Qu5 ermitteln: 4+9 Elemente = 36 minus 3 Mittelpunkte ist 33, zusammen 69. 36 und 33 sind gleichzeitig die ZS und FS der Zahlen 1-8. 69 und 37 sind die ZS der Buchstaben äußeren und inneren Quadratseite des SATOR-Quadrats:
|
|
3 Punkte + 2 Linien des Qu3 je Quadratseite werden zu 3 ungeraden und 2 geraden Punkten im Qu5. Das Verhältnis 2:3 wird im folgenden Punkt bedeutsam.
3. Wenn man die 4 Achsen des Quadrats in 8 Achsenarme aufteilt, ist die Differenz der Mittelpunkte 8-1 = 7. Numeriert man die 8 Achsenarme des Qu5 von 1-5, erhält man 8*15 = 120. Abzüglich 7 Mittelpunkte beträgt die Numerierungssumme 113, 48 für 16 Linien und 65 für 17 Punkte oder 1+8*14:
|
|
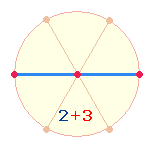
Die Einzelziffern der Summe 113 geben die Elemente der Kreisachse wieder, sie bestehen aus 2 Radiallinien und 3 Punkten:
|
|
Drei Achsen im Abstand von 60° geben die Gleichheit der drei göttlichen Personen wieder, die Einheit in der Dreiheit wird erkennbar in einem Mittelpunkt + 12 symmetrischen Elementen, wie auch im erweiterten Hexagramm, in dem das Kreisflächenverhältnis der beiden konzentrischen Tetraktyskreisen 1:(1+2) beträgt.
Wenn man jedem Radius einen Mittelpunkt zuordnet, kommt ein Mittelpunkt hinzu, sodaß man in vierstelliger Zusammensetzung 1113 schreiben kann.
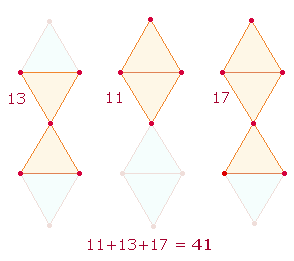
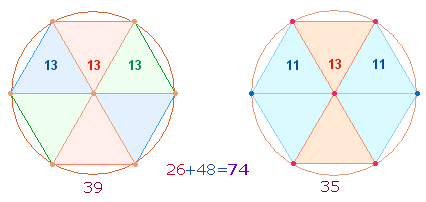
Verbindet man die 6 Kreislinienpunkte zum Hexagon, entstehen drei spiegelsymmetrische Doppeldreiecke, die zwei verschiedene Gestalten haben können:
|
|
Drei gleiche sanduhrförmigen Doppeldreiecke bestehen jeweils aus 13 Elementen. In der rechten Grafik stehen zwei Rautenfiguren aus jeweils 11 Elementen einander gegenüber, verbunden durch ein sanduhrförmiges Doppeldreieck. Nimmt man beide Figurengruppen zusammen, hat das mittlere Doppeldreieck Anteil an der Mittelachse durch 2 Mittelpunkte, die anderen beiden durch jeweils 5+3 Elemente, d.h. die Zahl der Elemente oben, in der Mitte und unten beträgt jeweils 8. Die 74 Elemente haben die Verteilung 28+18+28, die Zahl der linken, mittleren und rechten Elemente auf der oberen und unteren Ebene beträgt jeweils 4+6+4. Die Zahl der beanspruchten Elemente auf der Mittelachse ist links 11, rechts 7.
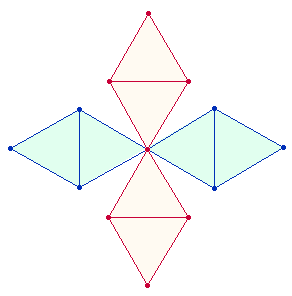
Aus jeweils vier der beiden geometrischen Figuren ist der Oktaeder zusammengesetzt. Er ist deshalb von besonderer Bedeutung, weil er die drei Achsen des Hexagons und die zwei Achsen des Quadrats durch ein DR-Kreuz in sich vereinigt:
|
|
Auch im Sinne von 2+3 Achsen können die Einzelziffern der Zahl 113 verstanden werden. Die Maßeinheiten 1+1 der Mittelachse sind deshalb so bedeutsam, weil 3+2 Achsen 6+4 = 10 Maßeinheiten des Dezimalsystems enthalten:
|
|
Die 13 Elemente der Hexagonachse und 9 Elemente des rechtwinkligen Achsenkreuzes werden besonders durch die Primzahl 139 wiedergegeben, wie die Doppelnumerierung der Kreisachse in vierstelliger Zusammensetzung zeigt:
|
|
Die Zahl 1112 hat die Faktoren 8*139.
4. Der bisherige Gang der Untersuchung zielt auf die sechs Umkehrungen der Zahl 134 ab:
|
|
|
|
|
|
|
|
sm |
FW |
sm |
FW |
|
UZ |
134 |
143 |
314 |
341 |
413 |
431 |
1776 |
48 |
|
|
|
FW |
69 |
24 |
159 |
42 |
66 |
431 |
791 |
120 |
|
|
|
|
|
|
|
862 |
862 |
|
|
|
|
|
|
sm |
2567 = 17*151 |
2567 |
168 |
2735 |
552 |
|||||
|
FW |
168 = 14*12 |
168 |
|
5*547 |
|
|||||
|
791 = 7*113;
48:120 = 24*(2:5); 552 = 23*24 |
||||||||||
Der Faktor 7 stellt die 7 Mittelpunkte dar, die von der Numerierungssumme der 8 Achsenarme 8*15 = 120 abzuziehen sind. Der zweimalige FW 168 ist auf die 16+8 Elemente der beiden äußeren Figurenpaare zu beziehen. Die Faktoren 14*12 geben in der Addition die 26 Elemente des Oktaeders wieder. Den Einzelziffern des Produkts 23*24 entsprechen 5 Durchmesser- und 6 Radialelemente der Kreisachse. 552 ist auch die ZS+FS des SATOR-Quadrats. Das Verhältnis 2:5 weist auf die 2+5 Punkte der DR hin.
Einen weiteren Hinweis auf die Zahlen 2+3 geben die zweimalige ZS+FS 862 = 2*431 durch 1:2 Zahlen und ihrer Gleichheit 1:1.
5. Umkehrungen zeigten sich in den ZS+FS 1555 = 5*311 und 1243 = 11*113. Der FW 1401 ihrer Summe 2798 = 2*1399 zeigt die Numerierungssumme eines einzelnen Achsenarms mit Abtrennung des Mittelpuktes durch eine 0.
Die FS der vier Umkehrzahlen beträgt 725 = 25*29. Beide Faktoren stellen Numerierungssummen mit 5 und 1 als Mittelpunkt. Sie ist zu erkennen bei der Winkelverschiebung des AK5 zum Qu5:
|
|
Beide Zählungen lassen sich als Strecke darstellen:
|
|
f)
Die 4 Achsen des SATOR-Quadrats
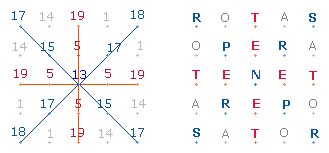
1. Die bisherigen Untersuchungsergebnisse kehren vielfältig in den vier Achsen des SATOR-Quadrats wieder:
|
|
Das Hauptergebnis soll bereits am Anfang vorgestellt werden:
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
243 |
209 |
452 |
15 |
30 |
45 |
497 |
|
452 = 4*113;
497 = 71*7; 243 = 35; 209 = 11*19 |
||||||
Jede der vier Achsen hat die durchschnittliche ZS+FS 113. Die FW 15 und 30 entsprechen den Summen der Zahlen 1-5 und 6-9.
Die Faktoren 11 und 19 sind als Doppelaspekt von 5+6 und 9+10 Durchmesser- und Radialelemente der beiden konzentrischen Kreise des Hexagramms zu verstehen. Sie können in einem Achsenkreuz dargestellt werden:
|
|
Die Einzelziffern der Faktoren 71*7 sind auf die 15 Rahmenelemente der DR zu beziehen:
|
|
2. Naturgemäß sind die beiden Diagonalachsen von besonderer Bedeutung:
|
|
Die
ZS der 2*4
Diagonalzahlen – außer der Mittelpunktzahl – beträgt 2*67 = 134. Die Zahl 67 ist in ihren Einzelziffern zu verstehen und auf 6 Linien und 5 Punkte
+ 2 Flächen des Doppeldreiecks zu beziehen.
Eine DR enthält zwei
dieser Doppeldreiecke, wenn die äußeren Punkte vereinigt werden.
Die ZS der Buchstaben SP ist 33, ihre FS 8+8 = 16, also um 17 niedriger. Dementsprechend beträgt die ZS+FS einer Diagonalhälfte 67+50 = 117 = 9*13. Durch Hinzufügung der Mittelpunktszahl 13 erhält man folgende 4Werte:
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
80 |
63 |
143 |
13 |
13 |
26 |
169 |
|
143
= 11*13 |
||||||
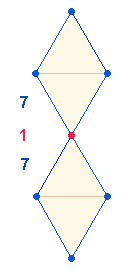
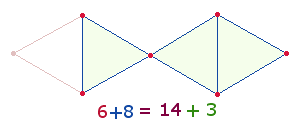
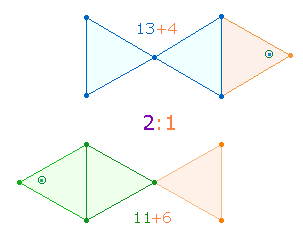
143 ist die markanteste der 6 Umkehrzahlen, erstens weil die beiden Faktoren 11 und 13 dem Faktor 113 am nächsten kommen, zweitens weil den Faktoren zwei geometrische Figuren entsprechen, aus denen alternativ der Oktaeder zusammengesetzt ist und drittens weil aus der Verbindung beider Figuren die "Fischfigur" hervorgeht, die aus 14+3 Elementen besteht, aus 6 Punkten + 8 Linien und 3 Flächen:
|
|
Die drei Flächen weisen auf die drei göttlichen Personen hin, da die Zahlen 9+8 (6+3; 8) die Komplementärzahlen zu 1 und 2 sind. Die Hinzunahme der FW fügt der Dreiheit noch die Einheit hinzu:
|
|
|
|
sm |
|
GS |
|
ZS |
6 |
3 |
9 |
8 |
17 |
|
FS |
5 |
3 |
8 |
6 |
14 |
|
sm |
11 |
6 |
17 |
14 |
31 |
Mit der anderen Diagonalhälfte ergibt sich das ZS+FS-Verhältnis 13*(11:9). Die Zahlen 11 und 9 stellen zwei komplementäre Achsenkreuze dar:
|
|
3. Zwei Zahlenverhältnisse ergeben sich, wenn die Mittelpunktszahl 13 der linken Diagonale zugeordnet wird:
|
|
Die ZS+FS beider Diagonalen sind:
|
Di. |
li. |
re. |
sm |
FW |
|
ZS |
77 |
70 |
147 |
17 |
|
FS |
63 |
50 |
113 |
113 |
|
|
140 |
120 |
260 |
130 |
|
77:70 = 7*(11:10) =
7*21 |
||||
|
140:120 = 10*(14:12) |
||||
Das auffälligste Ergebnis ist die FS 113, die damit ein Drittel der ZS 243 und der übrigen FS 96 bildet. Als ZS+FS 113 erscheinen auch die 6 Buchstaben einer Hälfte des inneren Quadrats:
|
|
Die 6 Buchstaben PERENE können zweimal horizontal und zweimal vertikal im stetigen Kreis gelesen werden. Es handelt sich um das Neutrum des – mit einem N geschriebenen – Adjektivs PERENNIS, -E – Ewig(es). Die 4Werte des Wortes sind:
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
63 |
50 |
113 |
13 |
12 |
25 |
138 |
|
138
= 2*69 |
||||||
Da 69 die ZS von SATOR ist, läßt sich die doppelte Summe als Umkehrungformel SATOR ROTAS – Schöpfer, du drehst verstehen.
Die ZS+FS 140:120 = 20*(7:5) = 10*(14:12) ist auf die 26 Elemente des Oktaeders beziehbar: auf 6 Ecken+8 Flächen und 12 Kanten.
4. Die FW der 8 Buchstaben des horizontal-vertikalen Achsenkreuzes sind gleich ihrem ZW. Die ZS+FS beträgt demnach 2*4*24 = 192. Das ZS+FS-Verhältnis der 9 Buchstaben der Diagonalachsen zu den 8 Buchstaben der horizontal-vertikalen Achsen beträgt demnach 260:192 = 4*(65:48). Tatsächlich beträgt die Summe der Punkte und Linien des numerierten AK5 – wie oben bereits festgestellt – 65 und 48.
5. Das SATOR Quadrat enthält als 8 Randbuchstaben der äußeren Eckbuchstaben viermal A und O. Ihre ZW 1 und 14 können als Numerierung von vier Achsenarmen betrachtet werden. Ihre FS:ZS-Verhältnis 40:60 = 10*(4:6) kann auf zweimal 10 Punkte von zwei Tetraktys bezogen werden.
Es sind nun vier ZS+FS des SATOR-Quadrats bestimmt worden: für die linke Diagonalachse 140, für die rechte 120, für das horizontal-vertikale Achsenkreuz 192 und die 8 Randbuchstaben 100. Die Gruppierungen 140+100 und 120+192 ergeben das Verhältnis 240:312 = 24*(10:13).
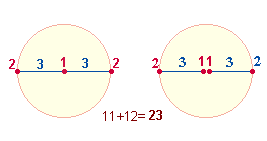
1. Wenn die Kreisflächenverhältnisse 1:3 und 1:2 so bedeutend sind, sollte man daran denken, daß die beiden ersten konzentrischen Quadrate aus 13 ungeraden und 12 geraden Zahlen bestehen:
|
|
Tatsächlich zeigen die 4W-Summen beider Gruppen die Bedeutung der Zahl 59 in einmaliger Weise:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
13
Z |
169 |
133 |
302 |
26 |
26 |
52 |
354 |
|
12
Z |
156 |
87 |
243 |
20 |
32 |
52 |
295 |
|
|
325 |
220 |
545 |
46 |
58 |
104 |
649 |
|
354:295
= 59*(6:5); 52 = 4*13 |
|||||||
|
649 = 11*59 = FW 70 |
|||||||
Sehr auffällig ist die zweimalige FW1/2-Summe 52. Die Einzelziffern 5 und 2 und die Faktoren 4*13 können mehreres bedeuten:
· Die
Einzelziffern 5 und 2
weisen auf ein DR-Kreuz mit zweimal 5+2 Punkte
einer DR hin.
· In
einer DR sind zwei "Fischfiguren"
erkennbar, sie bestehen aus 13 Elementen des hexagonalen Doppeldreiecks
und ein erweitertes Dreieck aus 4 Elementen:
|
|
· Wie
oben bereits dargelegt, sind die Einzelziffern des Produkts 4*13 als 4*(1:3)
auf das Erweiterungsprinzip von Quadratrahmen und als 4
= 1+3 auf die Punkte von zwei Rauten in der Doppelraute beziehbar.
Außerdem setzt sich der Oktaeder aus 4 Doppeldreiecken
zu je 13 Elementen zusammen.
Für 4=1+3 gibt einen weiteren Hinweis durch die ZS+FS der dreistelligen Umkehrungen 134 und 413:
|
ZS |
FS |
sm |
|
134 |
69 |
203 |
|
413 |
66 |
479 |
|
547 |
135 |
682 |
|
682
= 11*62 |
||
Die Einzelziffern von 62 lassen sich als 2*3 Punkte + 2 Mittelpunkte der DR interpretieren. Daneben erhält man das Verhältnis 1:3, da der FW von 62 33 ist. Auch aus 4 Rauten zu je 11 Elementen ist der Oktaeder zusammensetzbar. Die Zahl 413 selbst hat mit 7 den Teilungsfaktor 59.
2. Da sich eine fortlaufende Zahlenfolge nur auf den Punkten von Quadratrahmen verwirklichen läßt, ist die Vergleichbarkeit zwischen dem Qu5 und dem Hexagramm gewissermaßen nur asymmetrisch möglich. Den 13 ungeraden und 12 geraden Zahlen des Qu5 stehen 7 Punkte + 6 Dreiecke des Hexagons und 6 Punkte + 6 Dreiecke der hexagonalen Erweiterung gegenüber. Hinsichtlich des Qu3 und des Hexagons gibt es Gleichheit aller Elemente: 9 Punkte + 4 Quadrate = 13 und 12 Linien und 7 Punkte + 6 Dreiecke = 13 und 12 Linien.
Die 13 hexagonalen und 12 Erweiterungselemente geben das Kreisflächenverhältnis 1:2 wieder, die 13 hexagonalen und 25 Hexagrammelemente das Flächenverhältnis 1:3. Die Zahlen 13 und 25 sind auch die linken Eckpunkte des Qu5. Die rechten Eckpunktzahlen 17 und 21 lassen sich auf die Elemente der Fischfigur und der DR beziehen. Ihr Verhältnis ergibt sich aus der Zahl der Dreieck 3:4. Zusammengenommen erhält man so das Verhältnis 4:7.
3. 11 ist die Zahl der Umkehrung. Die Raute ist hierfür das beste Beispiel, indem sich einem Dreieck aus 7 Elementen ein weiteres aus 4 Elementen spiegelbildlich anschließt. Wie will man das Verhältnis 59*(5:6) des 4W-Ergebnisses auf das ganze Figur des Tetraktyssterns anwenden? Man könnte die 3 vertikalen Punkte und 8 Rahmenlinien der DR miteinander verbinden:
|
|
Eine weitere Umkehrung ist erkennbar: Den oben genannten 13 hexagonalen Elementen bzw. den ungeraden Zahlen des Qu5 entspricht die niedrigere Verhältniszahl 5.
4. Die Zahl 649 ist bei Berechnungen öfter anzutreffen. In ihr vereinigen sich offensichtlich einige bedeutsame Aspekte:
·
Die 10
Tetraktyspunkte lassen sich aufteilen in 6 hexagonale Punkte, dem Mittelpunkt und 3
Eckpunkte:
|
|
Dieser Punkteverteilung entspricht das Kreisflächenverhältnis 1:3. 9 ist die Zahl der Tetraktysdreiecke, die 3 Flächeneinheiten vertreten. Auf diese Weise kommen die 7 Punkte der DR und die 7 Kreisflächeneinheiten des Tetraktyssterns zustande. Die Einzelziffern der Zahl 649 und ihr FW 70 ergeben 19+7, was 19 DR-Punkten und 7 Flächeneinheiten entspricht:
|
|
Bei Umstellung von 19+7 ergibt sich dreistellig 719, die Summe von 649+70. Die Einzelziffern der neuen Summe lassen sich wiederum in 7 hexagonale und 10 Tetrakyspunkte aufteilen.
·
Die Produktzahlen 7*10
des FW 70 ist auf die hexagonalen und die
Tetraktyspunkte zu beziehen, sie geben das Kreisflächenverhältnis 1:3 bzw. das
Prinzip 1:3 in den ersten beiden
konzentrischen Quadraten und allen weiteren wieder.
5. Ein weiterer Aspekt enthält mehrere Bedeutungen und soll daher unter einer eigenen Nummer behandelt werden: Die Zahl 649 läßt sich zweistellig in 64+69+49 aufteilen:
|
Zahl |
64 |
49 |
69 |
182 |
|
FW |
12 |
14 |
26 |
52 |
|
|
76 |
63 |
95 |
234 |
|
52:182 = 26*(2:7) |
||||
|
76:95 = 19*(4:5); 171:63 = 9*(19:7) |
||||
·
Die FS 52, zusammengesetzt aus 2*26,
tritt wiederum auf wie bereits oben als zweimalige FW1/2-Summe.
Dort ist ihre mehrfache Bedeutung bereits besprochen. Die FW 12 und 14
geben die Aufteilung der 26 Oktaederelemente
wieder.
·
Zur Zahl
182 verweise ich auf einen eigenen
Eintrag.
·
Das
Verhältnis 19:7 ist erneut als 19 DR-Punkte
und 7
Kreisflächeneinheiten zu interpretieren.
·
Die ZS+FS 182+52 weist
bemerkenswerte Ähnlichkeiten mit dem SATOR-Quadrat
auf:
|
|
ZS |
|
SATOR |
69 |
|
OPERA |
52 |
|
TENET |
61 |
|
OPERA |
52 |
|
|
234 |
Die Bedeutung der vier von fünf Wörtern ist:
Der Schöpfer erhält seine Werke
durch seine Sorge.
Die 4*2 Diagonalzahlen des SATOR-Quadrats,
die oben behandelt wurden, haben die ZS 134 und die FS 100, zusammen 234.
·
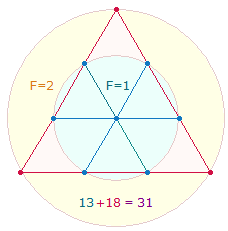
Die Produktzahlen 13*18
= 234 sind auf die Elemente der drei hexagonalen Achsen und drei
Tetraktysseiten beziehbar, sie geben das Kreisflächenverhältnis 1:3 wieder:
|
|
Erstellt: September 2016