Die Zahl 24
a) 2 und 4
im Kreis und Hexagramm
b) Zahlen- und Faktorensumme der Zahlen
1-24
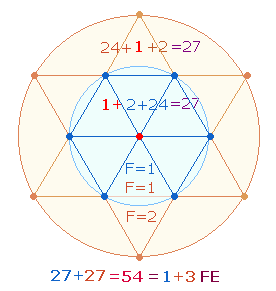
d) Zweimal 24 Elemente im Hexagramm
e) 4*6 und 3*8
Zwei parallele
Primzahlreihen von 1-1000
a) 2 und 4 in Kreis und Hexagramm
1.
Die Zahl 24 prägt unser Leben durch die Stunden des Tages, unterteilt in 12 Stunden für das Tageslicht, 12 für die Nacht. Wir sind wie
selbstverständlich an diese Zahl gewöhnt, obwohl sie von der 10-er Struktur des
Dezimalsystems abweicht. Sie erscheint besonders deswegen sinnvoll, weil wir
eine Tageshälfte in 2x6, 3x4 oder 4x3 Stunden einteilen können. Letztere Einteilung ist uns von den vier
Nachtwachen des römischen Heeres bekannt.
2.
Wie die Zahl 10 als Grundlage des Dezimalsystems auf der Verdoppelung der Primzahl 5 beruht, so die Zahl 6
auf der Verdoppelung der Primzahl 3, wie im folgenden darzulegen ist. Ausgangspunkt beider Zahlen ist der
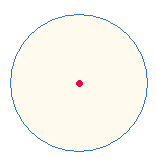
Kreis und seine Teilung in zwei Hälften. Der Kreis selbst besteht aus den 3 Elementen: Mittelpunkt, Kreislinie und Kreisfläche:
|
|
3. Ein Kreis wird in zwei Hälften
geteilt, indem man durch den Mittelpunkt eine Gerade zieht, die die Kreislinie
zweimal schneidet und als Durchmesser bezeichnet wird. Die Strecke zwischen dem
Mittelpunkt und einem Kreislinienpunkt wird Radius genannt.
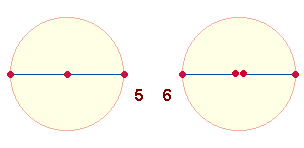
Das Streckenmaß des Radius und die beiden Begrezungspunkte bilden
3 Radialelemente. Da es im Durchmesser 2 Radialmaße gibt, verdoppeln
sich die Radialelemente auf 2x3=6 Elemente. Dabei wird der
Mittelpunkt zweimal gezählt:
|
|
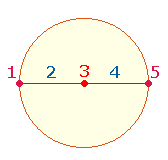
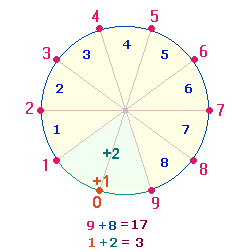
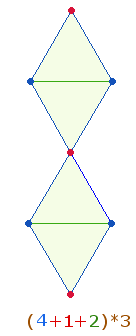
4. Der Durchmesser faßt die beiden
Radialmaße in 5 Elementen zusammen, 3 Punkten und 2 Linien. Diese 5 Elemente lassen sich der Reihe
nach von 1 bis 5 numerieren. Dabei besetzen die
Zahlen 2 und 4 die beiden Radiallinien. Die
Zahl 2 verbindet die Punkte 1 und 3, die Zahl 4 die Punkte 3 und 5. Die beiden Radiallinien halten linke und rechte
Seite im Gleichgewicht. Sie stellen die rationale Ordnung von Raum und Zeit
dar, während die Kreislinie auf die alles menschliche Begreifen übersteigende
Vollkommenheit Gottes hinweist. In den Zahlen 2 und 4 zeigt der geschaffene Kosmos abbildhaft die Gleichheit der 3 göttlichen
Personen, da 1+2+3 ebenso wie 2+(2+2) die
Zahl 6 ergeben:
|
|
3.
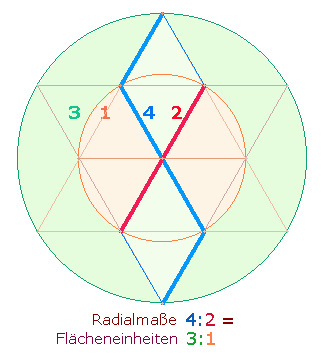
Bei der
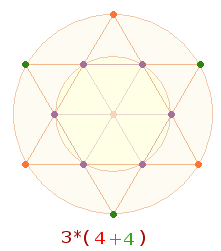
Erweiterung des Hexagons zum Tetraktysstern kommen zwei Radialmaße hinzu. Das Flächenverhältnis der beiden konzentrischen Kreise ist 1:3. Dieses
Verhältnis kann als analoge Beziehungen durch entsprechende Zahlen von
Elementen beider Bereiche wiedergegeben werden. Auf die Radialmaße bezogen ist
diese analoge Entsprechung 2:4:
|
|
Die beiden konzentrischen Kreise des
Tetraktyssterns begründen durch 2*5 Radialelemente das Dezimalsystem. Das Kreisflächenverhältnis 1:3
wird demnach durch 3:5 Radialelemente nach beiden Seiten hin wiedergegeben.
b) Zahlen- und Faktorensumme der Zahlen 1-24
1.
Der
Tetraktysstern besteht aus 49 Elementen, 25 gehören dem hexagonalen Bereich, 24 dem
Erweiterungsbereich an. Das erste Element ist der Mittelpunkt, die übrigen 48 Elemente
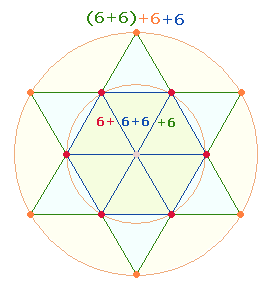
sind in symmetrische Gruppen von 6 Elementen einteilbar: das
Hexagon in 6 Punkte, 6 Achsenlinien, 6 Segmentlinien und 6 Dreiecksflächen, der Erweiterungsbereich in 6+6 Erweiterungslinien, 6 Schnittpunkte und 6 Dreiecksflächen:
|
|
Diese symmetrischen Elemente geben Flächenverhältnisse wieder, wenn um das Hexagramm ein Kreis geschlagen wird. Die Fläche des
Erweiterungsrings ist demnach doppelt so groß wie die des
Hexagons und die Fäche des äußeren Kreises dreimal so groß
wie die des inneren Kreises. Daher bedeuten 1:1 Elemente (6:6, 12:12 usw.) der beiden konzentrischen Bereiche das
Flächenverhältnis 1:2 und 1:2
Elemente (6:12, 12:24 usw.) das Flächenverhältnis 1:3. Die zweistellige Zusammensetzung der vier
Verhältnisse ergibt wiederum 48: 11+12 = 23; 12+13 = 25. Wie weiter unten gezeigt werden wird, ist die
Zahl 2325 die Zahlensumme (ZS) und Faktorensumme
(FS) der Zahlen 1-24, 1-30 und 1-36.
2.
Die
Analogiebeziehung zwischen Elementen und Flächengröße beruht auf dem Prinzip der Konzentrik der beiden Kreise. Dies gilt auch für das Hexagon
und seine Erweiterung zur Tetraktys. Ersteres besteht aus 25 Elementen, letztere aus 37 Elementen. Die Elemente des Hexagon stehen für 1
Flächeneinheit, die Tetraktys für 3. Treffen die Zahlen 25 und 37 in irgend einem Kontext zusammen, hat das
Additionsergebnis 62 oder Multiplikationsergebnis 925 die Bedeutung des Verhältnisses 1:3.
Die Tetraktys beweist ihre Identität
darin, daß die Zahlen 3 und 7 auf vierfache Weise
zusammenstimmen:
·
Sie besteht aus 37 Elementen.
· 7 Elemente gehören dem hexagonalen Bereich, 3 dem
Erweiterungsbereich an.
·
Jede der 3 Tetraktysseiten besteht aus 7 Elementen: 4 Punkten und 3 Linien:
|
|
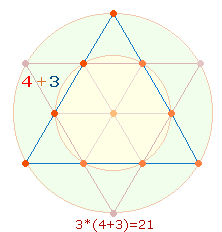
·
Den 3*(4+3) Elementen der Tetraktysseiten
entspricht die dritte Potenz von 7 der Zahl 343.
Der Zusammenhang
zwischen Tetraktys und den 1+48 Elementen des Hexagramms besteht darin, daß zwei Tetraktys aus jeweils 1+2+3+4 = 10 Punkten bestehen und die Multiplikation 1*2*3*4 zweimal 24 ergibt. Das Verhältnis beider Additionen 10+24 = 2*(5+12) ist auf die Elemente zweier Oktaederhälften zu beziehen: Eine Oktaederhälfte
besteht aus 5 Punkten (Ecken), 4+4 Linien
(Kanten) und 4 Flächen.
3.
Ein weiterer
Bezug zur Tetraktys zeigt sich in der Zahlensumme (ZS) 300 und der Faktorensumme (FS) 210 der
Zahlen 1-24. Das FS:ZS-Verhältnis
beträgt 30*(7:10). Setzt man die beiden
Verhältniszahlen mit 7 hexagonalen und 10
Tetraktyspunkten gleich, geben sie das Kreisflächenverhältnis 1:3 wieder, betrachtet man nur die
Differenz 3 zwischen 7 und 10, ist das wiedergegebene
Verhältnis 1:2.
Der gemeinsame Teiler 30 könnte sich auf je 10 Maßeinheiten der 3 Doppelrauten
im Hexagramm beziehen.
4.
Es scheint in
der Logik des Zahlensystems zu liegen, daß eine gerade und ungerade Zahlenmenge
addiert und als Einheit zu sehen ist. Hinsichtlich der 49 Elemente des Hexagramms ist also 49+48 zum
Ergebnis 97 zu
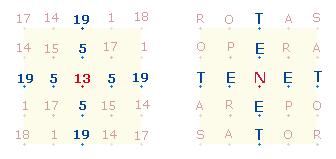
addieren. Diesen Zusammenhang jedenfalls ist im SATOR-Quadrat zu erkennen: Denn die ZS des inneren Quadrats beträgt 97. Die Faktorenwerte der Zahlen 49 und 48 sind 14+11 = 25. 97+25 ergibt 122 = 2*61. Die
ZS einer TENET-Achse
beträgt 61:
|
|
Die Einzelziffern der Zahl 61 sind als 6 Punkte und Mittelpunkt
sowohl des Hexagons als auch der Erweiterung zu verstehen. Das heißt, der
Kreisbogen der Erweiterung gehört notwendig zum Hexagramm.
Nimmt man also den zusätzlichen
Mittelpunkt für die Erweiterung noch hinzu, erhält man für beide Bereiche je 25 Elemente, zusammen 50. Der FW 50 ergibt sich aus der Zusammensetzung von 48+1 Elementen
in der Zahl 481 = 13*37. Die beiden Faktoren sind
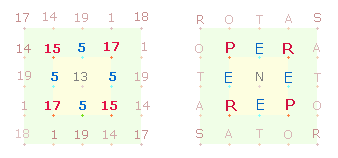
zu lesen als 13 und 3+7, also 13 Punkte des Hexagramms und 10 Punkte der Tetraktys. Die
Faktoren der Umkehrzahl 148 sind 4*37 = FW 41. Tatsächlich ist die ZS jeder Seite des inneren Quadrats 37:
|
|
Die Summe der beiden FW ist 91 = 7*13. Die Zahl 91 ist die
Summe der Zahlen 1-13, gleichzeitig bedeuten 7:13 Punkte des Hexagons und des ganzen Hexagramms das Kreisflächenverhältnis 1:3.
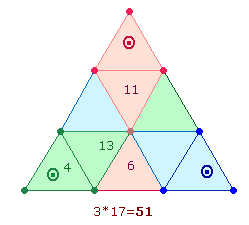
1.
Die
trinitarischen Zahlen 1 und 3, die aus dem
Kreisflächenverhältnis 1:3 hervorgehen, setzen sich im zweistelligen
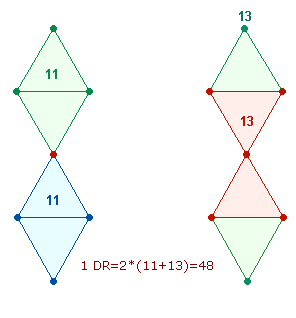
Bereich durch die Zahlen 11 und 13 fort, die zusammen 24 ergeben. Aus 11 und 13 Elementen bestehen auch die
folgenden beiden Figuren, aus denen sich der Oktaeder zusammensetzt, wenn man ein Achsenkreuz aus zwei Doppelrauten bildet:
|
|
2.
Aus 22+26 Elementen ist also ein Oktaeder zusammensetzbar, wahlweise aus 4*11 oder 4*13.
d) Zweimal 24 Elemente im Hexagramm
1.
Nach der
bisherigen Betrachtung entsteht die Zahl 24 durch
Zusammensetzung von 2 und 4. Im voll ausgebildeten
Dezimalstern sind die 2 Radiallinien auf wirkliche 24 Linien erweitert. Dabei entfallen 12 Linien auf
das Hexagon und 12 Linien auf die Erweiterung zum Hexagramm:
|
|
Der konzentrische Doppelkreis, der den
Dezimalstern enthält, erweist sich darin als Grundlage des Dezimalsystems, daß
die 3 Radialelemente um 2 auf 5 Elemente erweitert werden und durch Verdoppelung die zyklische Zahl 10 ergeben.
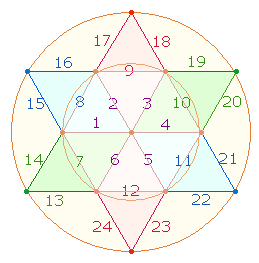
Die 2*12 Linien lassen sich in stetigem Umlauf von innen
nach außen in drei Folgen numerieren, zwei für den hexagonalen und zwei für den
Erweiterungsbereich:
|
|
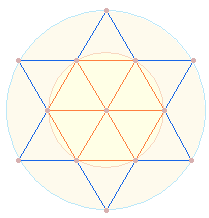
Im Tetraktysstern sind 6 Rauten zu erkennen, drei oben
und drei unten. Deren 4Werte sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
li. ob. |
42 |
25 |
67 |
12 |
10 |
22 |
89 |
|
Mi. ob. |
49 |
36 |
85 |
14 |
10 |
24 |
109 |
|
re. ob. |
56 |
42 |
98 |
13 |
12 |
25 |
123 |
|
sm |
147 |
103 |
250 |
39 |
32 |
71 |
321 |
|
li. un. |
63 |
43 |
106 |
13 |
43 |
56 |
162 |
|
Mi. un. |
70 |
49 |
119 |
14 |
14 |
28 |
147 |
|
re. un. |
41 |
35 |
76 |
41 |
12 |
53 |
129 |
|
sm |
174 |
127 |
301 |
68 |
69 |
137 |
438 |
|
GS |
321 |
230 |
551 |
107 |
101 |
208 |
759 |
|
759 =
3*23*11 >FW 37 |
|||||||
Die Gesamtsumme 759 ist ZS+FS 465+294 der Zahlen
1-30.
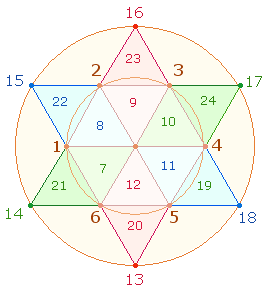
Hexagon und Erweiterung bestehen weiterhin aus
jeweils 6 Punkten und 6 Dreiecken. Die
Numerierung beginnt jeweils mit den Punkten:
|
|
Die 4Werte der 6 Rauten haben folgende Ergebnisse:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
li. ob. |
48 |
30 |
78 |
11 |
10 |
21 |
99 |
|
Mi. ob. |
53 |
42 |
95 |
53 |
12 |
65 |
160 |
|
re. ob. |
58 |
40 |
98 |
31 |
11 |
42 |
140 |
|
sm |
159 |
112 |
271 |
95 |
33 |
128 |
399 |
|
li. un. |
57 |
47 |
104 |
22 |
47 |
69 |
173 |
|
Mi. un. |
56 |
39 |
95 |
13 |
16 |
29 |
124 |
|
re. un. |
49 |
32 |
81 |
14 |
10 |
24 |
105 |
|
sm |
162 |
118 |
280 |
49 |
73 |
122 |
402 |
|
GS |
321 |
230 |
551 |
144 |
106 |
250 |
801 |
|
399:402 = 3*(133:134) = 3*267 = 9*89 |
|||||||
Die Werte der beiden Tabellen werden nun addiert, nach oberen und unteren
Rauten geordnet:
|
|
147 |
103 |
250 |
39 |
32 |
71 |
321 |
|
|
159 |
112 |
271 |
95 |
33 |
128 |
399 |
|
sm |
306 |
215 |
521 |
134 |
65 |
199 |
720 |
|
|
174 |
127 |
301 |
68 |
69 |
137 |
438 |
|
|
162 |
118 |
280 |
49 |
73 |
122 |
402 |
|
sm |
336 |
245 |
581 |
117 |
142 |
259 |
840 |
|
GS |
642 |
460 |
1102 |
251 |
207 |
458 |
1560 |
|
720:840 = 120*(6:7) = 10*12*13 |
|||||||
|
306:336 =
6*(51:56) |
|||||||
306+181
Die ZS+FS 551 ist in beiden Tabellen gleich. Die Faktoren 19*29 = FW 48 sind auf ein Kreis- und ein Streckenmodell von 10 und 11 Punkten zu beziehen:
|
|
|
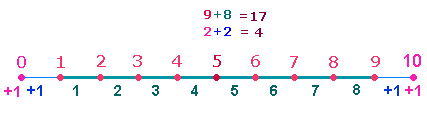
In beiden Fällen ist der erste Punkt die Null. Im
Kreismodell führen die Zahlen 1-9 wieder zur Null zurück, im
Streckenmodell wird die Zählung fortgesetzt. In beiden Modellen ist das Muster 1-8-1 der Maßeinheiten gleich. Die beiden Randeinheiten als Querlinien der
Doppelraute und werden bei der Oktaederbildung zur quadratischen Mittelbasis.
Die Einzelziffern der Zahl 551 geben 5+5 Maßeinheiten
und 10+1 Punkte wieder:
|
|
Die Einzelziffern der FW1/2-Summe 458 = 2*229
läßt sich auf die Elemente einer Oktaederhälfte beziehen: 4 Flächen,
5 Punkte, 8 Linien (Kanten), die der Zahl 229 auf
die 9 Elemente des rechtwinkligen Achsenkreuzes und – unter
Hinzufügung von 2+2 weiteren Elementen die 13
Elemente des hexagonalen Achsenkreuzes.
2. Die Faktoren 19 und 29 der Zahl 551 erscheinen im Endergebnis, wenn man zu den ZS und FS ihre FW-Summen stellt:
|
|
ZS |
FW1 |
sm |
FS |
FW2 |
sm |
GS |
|
GS |
642 |
251 |
893 |
460 |
207 |
667 |
1560 |
|
893 = 47*19 >FW 66; 667 = 23*29 >FW 52 |
|||||||
|
207:460 = 23*(9:20) |
|||||||
|
66+52 = 118 |
|||||||
Der FW 66 weist auf die 6 Rauten des Hexagramms hin, der FW 52 auf 4 sanduhrförmige Doppeldreiecke, aus denen der Oktaeder zusammengesetzt ist.
Die FS 118 zeigt das Muster der 10 Maßeinheiten des Dezimalsystems.
3. Die Zahl 551 ist deshalb
so bemerkenswert, weil sie die ZS+FS der
Kreuzesinschrift ist:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
IESUS |
70 |
36 |
106 |
14 |
10 |
24 |
130 |
|
NAZARENUS |
111 |
90 |
201 |
40 |
13 |
53 |
254 |
|
sm |
181 |
126 |
307 |
54 |
23 |
77 |
384 |
|
REX |
43 |
32 |
75 |
43 |
10 |
53 |
128 |
|
IUDAEORUM |
102 |
67 |
169 |
22 |
67 |
89 |
258 |
|
sm |
145 |
99 |
244 |
65 |
77 |
142 |
386 |
|
GS |
326 |
225 |
551 |
119 |
100 |
219 |
770 |
|
FW |
165 |
18 |
181 |
24 |
14 |
38 |
219 |
|
326 =
2*163; 384 = 8*48; 386 = 2*193 |
|||||||
|
219 =
3*73 |
|||||||
Die 2+2 Wörter bestehen aus 14 und 12 Buchstaben, das entspricht 6 Ecken + 8 Flächen und 12 Kanten des Oktaeders. Die geraden 4W-Summen 384 und 386
liegen nebeneinander und sind konstitutiv für ihre Summe 770. Die Faktoren 7*10*11 sind auf 7+10 Punkte des
Hexagons und der Tetraktys und auf 10+11 Elemente
der DR beziehbar. In einer
spezielleren Funktion stellen sie einen Doppelaspekt der Raute dar, die einerseits
aus 11 Elementen andererseits aus zwei Dreiecken von je 7 Elementen besteht. Da der FW von 10 7 ist, kommen auf diese Weise die Elemente von zwei
Dreiecken zusammen. Der Doppelaspekt 11+14 der Raute
ergibt 25, der
Doppelaspekt 13+14 des sanduhrförmigen Doppeldreiecks 27. Das Additionsergebnis 52 = 4*13 ist wiederum auf die Zusammensetzung des
Oktaeders beziehbar.
Die Einzelziffern der Faktoren 163 und 193 geben die 10 Punkte der
Tetraktys und 13 Punkte des Hexagramms wieder, 13 Punkte ebenso die Faktoren 3*73.
Die ZS+FS der
beiden Numerierungen (N.) und der Kreuzesinschrift (In.) liegen jeweils nur 5 Zähler auseinander, können also aufeinander bezogen
betrachtet werden.
Wir können von den vier Wörtern je zwei den drei
oberen und unteren Rauten des Tetraktyssterns zuordnen und jeweils drei
Zählungen addieren:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
2 N. |
306 |
215 |
521 |
134 |
65 |
199 |
720 |
|
In. |
181 |
126 |
307 |
54 |
23 |
77 |
384 |
|
sm |
487 |
341 |
828 |
188 |
88 |
276 |
1104 |
|
2 N. |
336 |
245 |
581 |
117 |
142 |
259 |
840 |
|
In. |
145 |
99 |
244 |
65 |
77 |
142 |
386 |
|
sm |
481 |
344 |
825 |
182 |
219 |
401 |
1226 |
|
|
968 |
685 |
1653 |
370 |
307 |
677 |
2330 |
|
968 = 8*11²; 2330 = FW 240 |
|||||||
Auf eine ausführliche Auswertung der Ergebnisse
soll hier verzichtet und nur kurz auf die auffälligsten eingegangen werden:
· Der FW 240 kehrt zum Thema der Zahl 24 zurück.
· Der soeben behandelte Doppelaspekt von 25 und 27 Elementen erscheint als die Faktoren 27*25 der ZS 487 + ihrer FW-Summe 188. Der FW der Summe 675 ist 19.
Der FW der parallelen Summen 481+182 = 663 = 3*13*17 beträgt 33. Die beiden FW ergeben
erneut 52. In der
Tetraktys finden sich von den drei Ecken her gesehen zwei geometrische Figuren:
das Doppeldreieck aus 13 und die "Fischfigur" aus 17 Elementen:
|
|
Der FW 33 ist auch die Summe von 3*11 Elementen der Raute.
· Das Verhältnis der FW1/2-Summe 276 zur ZS+FS 828 ist 276*(1:3). 276 = 12*23 ist die Summe der Zahlen 1-23. 276 kann in 4*69 aufgeteilt werden und bildet dann die ZS von SATOR/ROTAS der
vier Seiten des SATOR-Quadrats.
· Die Zahl 481 wurde bereits oben behandelt,
sie stellt eine Zusammensetzung aus 48+1 Elementen dar und ist durch 37 teilbar.
· Die beiden FW-Summen
188 und 182 sind
gematrische Werte von CHRISTUS (112+76) und IESUS (70) CHRISTUS (112).
· Die FW1/2-Summen
370 und 307 weisen auf die Punkte von zwei
Tetraktys hin. Die Summe 677 ist eine Primzahl. Die
Einzelziffern sind einmal auf die Punkte der Erweiterung und zweimal auf die Punkte
des Hexagons zu beziehen. Demnach bedeuten (6+7)+7 Punkte
(2+1)+1 Flächeneinheiten.
5.
Die Zahl 24 ergibt sich auch, wenn man für jede drei Seiten von zwei Tetraktys jeweils
4 Punkte zählt:
|
|
Eine zweite Möglichkeit für 24 Elemente bietet ein DR-Kreuz, das zu einem Oktaeder zusammengesetzt werden kann. Wenn man zwei Rautenlinien mit Punkt in der
Mitte als eine 3-er Einheit auffaßt, ergeben sich für eine DR 4x3 = 12 "Dachelemente", verdoppelt 24.
Der Vollständigkeit halber sei noch hinzugefügt,
daß weitere 3 Einheiten zu je 3 Elementen
zustande kommen, wenn man den Mittelpunkt sowie den untersten
und obersten Punkt als eine Einheit auffaßt. Es bleiben 2 Einheiten übrig, die durch zwei Dreiecke mit dazwischen liegender
Trennungslinie gebildet werden:
|
|
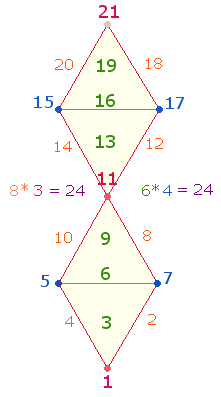
1.
Von der Zahl 24 lassen sich zwei einstellige Produkte bilden, deren Addition 10+11 = 21 beträgt. Die vier Einzelziffern lassen sich den 21
Elementen der Doppelraute so zuordnen, daß 4 Zähler auf
die Querpunkte fallen, 6 auf die Binnenelemente, 3 auf die Vertikalpunkte und 8 auf die Rahmenlinien. Die 21 Elemente sind von unten nach oben zickzackweise numeriert:
|
|
Von den vier Gruppen lassen sich die 4Werte ermitteln:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
4 |
44 |
37 |
81 |
15 |
37 |
52 |
133 |
|
6 |
66 |
54 |
120 |
16 |
11 |
27 |
147 |
|
sm |
110 |
91 |
201 |
31 |
48 |
79 |
280 |
|
3 |
33 |
22 |
55 |
14 |
13 |
27 |
82 |
|
8 |
88 |
52 |
140 |
17 |
17 |
34 |
174 |
|
sm |
121 |
74 |
195 |
31 |
30 |
61 |
256 |
|
GS |
231 |
165 |
396 |
62 |
78 |
140 |
536 |
|
201:195 = 3*(67:65); 280:256 = 8*(35:32) = 8*67 |
|||||||
|
133:147 = 7*(19:21) |
|||||||
Das Summenverhältnis von 4:12 Einzelwerten beträgt 67*(3:5). Den Verhältniszahlen 35:32 entspricht ein Achsenkreuz
AK9 aus 35 Punkten und 32 Linien.
Das FS:ZS-Verhältnis der 6 Binnenelemente beträgt 6*(9:11). Den Verhältniszahlen 9:11 entsprechen zwei Achsenkreuze aus 9 und 11 Elementen. Der durchschnittliche ZW+FW je Zahl ist demnach 20.
Ein Oktaeder hat 6 Ecken + 8 Flächen = 14 Elementen
und 12 Kanten. Die ZS+FS 140 und
120 spiegeln diese beiden Zahlen von Elementen wider.
2.
Die vier
Produktzahlen treten bei der Oktaederbildung auf folgende
Weise in Erscheinung:
Der DR-Rahmen besteht aus 7 Punkten und 8 Linien. Die Zahl von 7 Punkten reduziert sich beim Zusammenfall des untersten mit dem obersten
Punkt auf 6.
Die beiden Zickzack-Durchmesser der
Doppelraute bestehen aus jeweils 9 Elementen. An den 3 vertikalen Schnittpunkten haben auch die 6
Binnenelemente teil. Die 3*7 Elemente der Doppelraute sind
also von eigentlich 3*9 Elementen reduziert. Nach Wegfall eines Punktes
besteht jede der 3 Durchmesserkomponenten aus nur 8 Elementen.
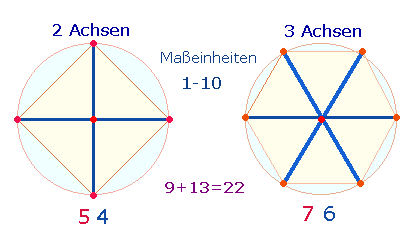
Die Zahlen 4 und 6 ergeben 10
Maßeinheiten, die im rechtwinkligen und hexagonalen Achsenkreuz enthalten sind:
|
|
3.
Multiplikation
und Addition der Produkte 3*8 und 4*6 ergeben 24+11 = 35 und 24+10 = 34 und damit die ZS des Wortes SATOR, aufgeteilt in die Randbuchstaben SR (35) und die Mittelbuchstaben ATO (34).
1.
Man hat schon
lange herausgefunden, daß Primzahlen, von den Ausgangszahlen 1 und 5 an stets in 6-er Schritten erscheinen. Der Zahl 24 scheint dabei eine besondere Rolle zuzukommen. Der Chemiker Peter Plichta hat darauf sein Primzahlkreuz gegründet und darüber ein gleichnamiges Buch verfaßt.
Die 24
symmetrischen Elemente des Hexagon lassen sich, wie oben bereits erwähnt, in 4*6 Einheiten aufteilen: 6 Kreislinienpunkte, 6 Achsenlinien, 6 Segmentlinien und 6
Dreiecksflächen.
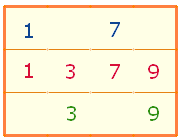
2. In den beiden Zahlenreihen gibt es bis 24 jeweils 4 Primzahlen:
|
|
1 |
|
|
|
7 |
|
|
|
13 |
|
|
|
19 |
|
|
56 |
13 |
|
|
|
|
5 |
|
|
|
11 |
|
|
|
17 |
|
|
|
23 |
40 |
11 |
|
Abst. |
|
4 |
|
2 |
|
4 |
|
2 |
|
4 |
|
2 |
|
4 |
|
96 |
24 |
Der Abstand zwischen den beiden
Reihen beträgt abwechselnd 4 2 4 und 2 4 2. Die FW 13 und 11 der Summen 56 und 40 ergeben als Summe 24 und
verweisen auf die beiden geometrischen
Figuren, aus denen der
Oktaeder zusammengesetzt ist. Die Zahl 96 ist
gewissermaßen die Vollzahl des Oktaeders, da er alternativ aus 4 Rauten oder 4
Doppeldreiecken zusammengesetzt werden kann. Auch die Summe 76128 der 169 Primzahlen von 1-1000 ist
durch 96 teilbar.
Die 8 Primzahlen haben
den Durchschnittswert 12.
3. Für Holger Ullmann ist die Zahl 24 ein Dreh- und Angelpunkt seiner Website über die TETRAKTYS, die
nach seiner unumstößlichen Auffassung nichts mit dem Dezimalsystem zu tun habe.
Bezeichnenderweise stellt er sie in seinem Logo nur aus Punkten dar. Obwohl er
die Zahl 1 nach
einigem Hin- und Herüberlegen als Primzahl anerkennt, schließt er sie etwa bei
der Betrachtung
der Zahl 7 in der Offenbarung des Johannes aus. Denn er
sagt, bis 24 seien es 7 Primzahlen
(statt 8):
|
|
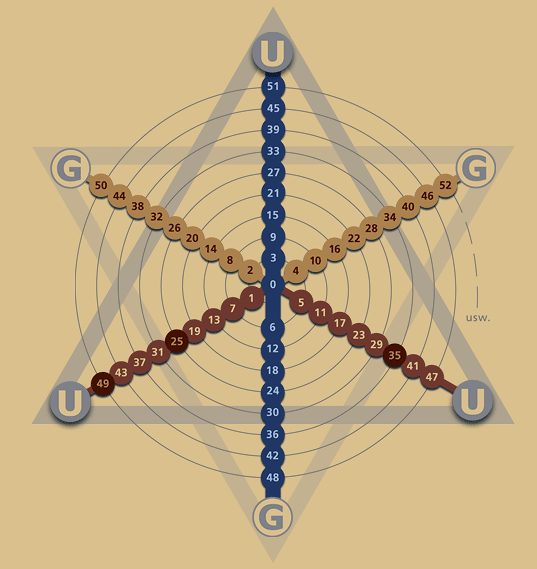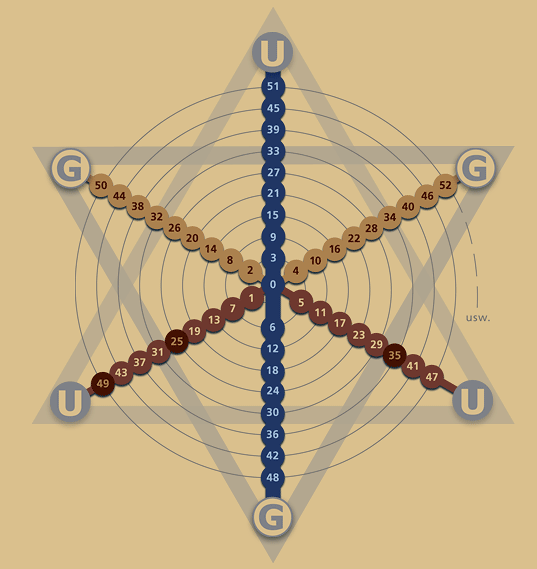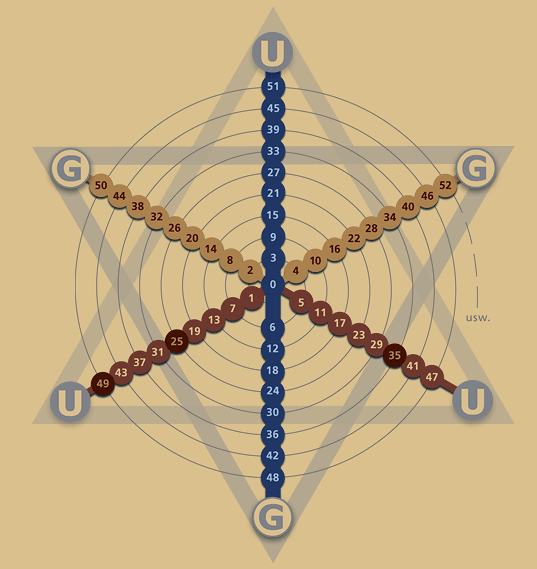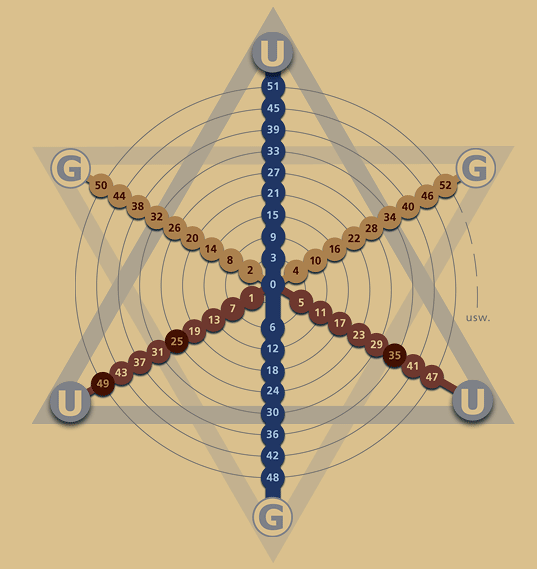
In vorstehender Grafik stellt er
seinen "6-er Wendel" in die 6 Ecken der Tetraktys, obwohl es
natürlicher wäre, ihn mit den drei Hexagonachsen gleichzusetzen. Die Zahl 1 erscheint hier als Primzahl. Tatsächlich scheint es eine Ordnung zu geben,
wenn man die Primzahlen in zwei Reihen erstellt, z.B. von 1-97:
1 7 13 19 31 37 43 61 67
73 79 97 = 528 = 11*48
5 11 17 23 29 41 47 53 59
71 83 89 = 528 = 12*44
Für jede Reihe aus 12 Primzahlen ergibt sich dieselbe Summe 528 mit dem Durchschnittswert 44. Eine weitere Klärung versuche ich am Ende dieser Untersuchung. Dieselbe
Summe 528 kommt zustande, wenn man die ersten beiden Zahlenpaare in
Zusammensetzung addiert: 17+511
= 528. Die Faktoren
der Zahl 511 sind 7*73 und bedeuten wie die Aufteilung der Zahl 17 in 7+10: 7 Punkte des Hexagon und 10 Punkte der Tetraktys. Die FW beider Zahlen sind 17+80 = 97, die letzte Primzahl der ersten 100-er Einheit.
Das Problem dieses Modells beginnt dann, wenn sie mit Deutungen und
Wertungen verbunden wird: Bis 24 seien die Primzahlreihen noch
vollständig, die Zahl 25 als Quadratzahl von 5 sei die erste "Pseudo-Primzahl". Daraus schließt er folgendes:
"Bis zur Zahl 24 ist das 'Paradies' noch in Ordnung.
Ab der Zahl 25 beginnt der 'Sündenfall', der Fall in die 'Materie'. Die Ziffer
5 ist die 'Zahl des Menschen'".
Dieses Modell ist Ullmann deshalb
heilig, weil er im Dezimalsystem keine ontologische Ordnungskategorie sieht,
sondern ein "von Menschen frei gewähltes hierarchisches Zählsystem".
Er hat also kein Vertrauen in ein Modell, das auf der Zyklik von
Zehnereinheiten gründet.
4. Üblicherweise werden nämlich zur Bestimmung von
Primzahlen alle Zahlen, die durch 2, 3 und 5 teilbar sind,
"ausgesiebt". Übrig bleibt ein Schema von Einerstellen, das sich nach
drei 10er Einheiten wiederholt:
|
|
Ullmanns Beharren auf sein 24-er
Modell gibt Anlaß zur Frage, ob man nicht mehr als ein Modell annehmen sollte
und ob es vielleicht im Tetraktysstern anzutreffen ist. Tatsächlich enthalten
die drei Doppelrauten des Hexagramms jeweils 10 Linien oder Maßeinheiten und weiterhin 6 Punkte (ohne
Mittelpunkt) und 4 Dreiecksflächen. Auch die drei Doppelrauten
könnte man von 1-30 doppelt numerieren, wie es oben mit der Zahl 24 geschehen ist. Und dann gibt es noch die beiden Tetraktys selbst, die
jeweils 18 Linien enthalten, und weiterhin 9 Punkte und 9 Dreiecke.
5.
Die
Verwandtschaft der Zahlen 24 und 30 zeigt
sich in ihren FS. Sie ist für
1-24 210 und für 1-30 294. Ihr Verhältnis ist 42*(5:7).
Die beiden Zahlen zusammen bilden mit dem
Additionsergebnis 54 = 2*27 eine
wesentliche Zahl für die Elemente des Tetraktyssterns. Demnach besteht das
Hexagon und seine Erweiterung aus jeweils 24
symmetrischen Elementen und zwei Kreisen mit den 3 Elementen Mittelpunkt,
Kreislinie und Fläche:
|
|
Vom trinitarischen Standpunkt
ergeben die Einzelziffern 1 2 3 und 9 8 7 komplementär jeweils 10. Addiert betragen die Summen 6 und 24, zusammen 30.
Bemerkenswert auch die Faktorensummen 6 und 19 der zwei Zahlenreihen. Zu den ZS hinzugefügt,
ergibt sich 6+6 = 12 und 24+19 = 43, zusammen 55, die Summe der Zahlen 1-10 aus den Ziffern 1-4. 619 ist der Faktorenwert der ersten vier Zahlen 1234.
6.
Nun sind noch
die 36 symmetrischen Elemente der beiden Tetraktys
hinzuzunehmen. Das Verhältnis 24:36 ist 12*(2:3) und 54:36 ist 18*(3:2).
Die ZS und FS der Zahlen 1-36 zeigen eine
innere Beziehung zu 24 und 30:
|
|
ZS |
FS |
sm |
Faktoren |
|
1-24 |
300 |
210 |
510 |
30*17 |
|
1-30 |
465 |
294 |
759 |
69*11 |
|
1-36 |
666 |
390 |
1056 |
96*11 |
|
|
1431 |
894 |
2325 |
75*31 |
|
FW |
62 |
154 |
216 |
|
|
1431 = 27*53; 894 = 6*149; 216 = 6³ |
||||
|
465 = 15*31 |
||||
Die Gesamtsumme 2325 enthält den Faktor 31 wie die Summe der Zahlen 1-30 – ein Hinweis darauf, daß die anderen beiden Zahlenreihen auf die
Mittelzahl 30 ausgerichtet sind. Das Zahlenverhältnis ist 465*(1:4). Die Zahlen 23 und 25 sind die Konstitutivzahlen ihrer Summe 48, die als 2*(11+13) aufgefaßt und auf die Zusammensetzung des
Oktaeders bezogen werden kann.
Eine weiterer Bezug zur FS 294 der Zahlen 1-30 zeigt sich
in der Addition 510+666 = 1176 = 4*294 = 294*(1:4) = 1470. Übrig bleiben 465+390 mit den Umkehrfaktoren 31 und 13: 15*(31+26) = 15*57 =
45*19 = 855. Auch der FW des
Gesamtergebnisses ist aus beiden Umkehrzahlen gebildet: 75*31 = FW 13+31 = 44.
Die ZS+FS der
Zahlen 1-30 und 1-36 sind engstens auf einander
bezogen durch den gemeinsamen Faktor 11 und die Umkehrungen 69 und 96. Letztere kommen auch zustande durch die Additionen 300+390 = 690 und 666+294 = 960 = 3*10*(23+32) = 30*55. 55 ist die Summe der Zahlen 1-10.
Den Faktoren 11 und 10 beider Additionspaare entsprechen 11+10 Elemente
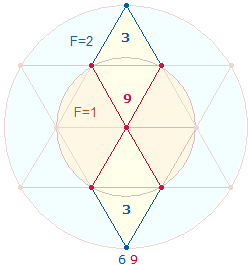
der DR. Die Einzelziffern 9 und 6 sind auf die Rahmenelemente der DR beziehbar: 9 gehören zum
hexagonalen Bereich, 6 zum Erweiterungsbereich, 6 ist außerdem der FW von 9:
|
|
Die FS 216 = 6³ weist auf die
Dreidimensionalität des Oktaeders und seinen 6 Ecken.
7.
Zweifellos
besteht eine wesentlicher Zusammenhang der beiden Zahlen 6 und 10:
· Die Kreisachse besteht aus
zweimal 3 Radialelementen, die
Zickzacklinie der Doppelraute aus zweimal 5 Elementen:
|
|
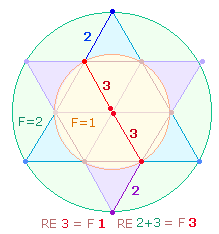
6:10 oder 3:5
Radialelementen entspricht das Kreisflächenverhältnis 1:3. Hinzukommen 3:2
Radialelemente, die das Verhältnis 1:2 darstellen. So werden 4+3 = 7 Flächeneinheiten zweimal durch 8+5 = 13 Radialelemente wiedergegeben.
· 6+10 Radialelemente ergeben die Quadratzahl 16, die aus den Summen der benachbarten Zahlenreihen 1-3 und 1-4 zustande
kommt. Die Endzahlen 3 und 4 entsprechen nicht nur den 7 Flächeneinheiten, sondern sind durch
3 Maßeinheiten und 4 Punkte jeder
einzelnen Tetraktysseite vertreten.
· 6 und 10 sind
gemeinsam teilbar durch die Zahl 30. Auch dieser
Umstand spricht für das oben angeführten 30-er Muster der
Primzahlverteilung.
8.
Untersuchen
möchte ich noch die Primzahlsummen in den drei Zahlenreihen 1-24, 1-30 und 1-36. Nach dem 30-er Muster entfallen die Primzahlen 2 3 5. Nach meiner Erfahrung sind die drei Primzahlen LIBERO-Zahlen, sie können je
nach Bedarf zu einer Primzahlsumme hinzugefügt werden, um ein Zahlenverhältnis
zu ermöglichen. Sie sind wohl mit den in obiger Grafik gezeigten 2+3+(3+2) Radialelementen der beiden Tetraktyskreise in
Verbindung zu bringen und von mir schon früher untersucht worden.
Geht man von drei Primzahlen aus,
gibt es 6 Möglichkeiten der Hinzufügung – und ohne Hinzufügung – 7 Variablen einer Primzahlsumme: 0, 2, 3, 5, 7, 8, 10. Die Zahl 5 erscheint als konzentrische
Mitte von drei Paaren, die sich jeweils zur komplementären Summe
10 addieren. Ergibt sich ohne die Gesamtsumme 10 der drei Primzahlen kein Zahlenverhältnis, kann dies durch
eine dieser Hinzufügungen erreicht werden.
Als Beispiel der 7 Möglichkeiten diene die Summe 1051 der 23 Primzahlen von 1-97: Die konzentrische Mitte ist 1056, die ZS+FS der Zahlen 1-36: 1056 = 25*3*11 = FW 13+11 = 24. Die Summe versiebenfacht sich und der FW ist demnach 31, übrigens derselbe wie von der Zahl 1001 = 7*11*13. Die FS dieser 7 Zahlen ist 2615 =
5*523 = 528 = 48*11 = 22. Der Faktor 523 enthält die
drei LIBERO-Zahlen.
9.
Die
Primzahlsumme 96 (unter Einschluß der Zahl 5) kann für die Zahlen 1-24 sowohl mit der ZS 300 als auch mit der FS 210 ein Verhältnis bilden: 96:204 =
12*(8:17), 96:114 =
6*(16:19)
und 96+96 = 192:318
= 6*(32:53). 3:2 und
5:3
Radialelementen entsprechen die Kreisflächenverhältnisse 1:2 und 3:1.
Läßt man
die Zahl 5 weg,
ist nur ein FS-Verhältnis möglich: 91:119 = 7*(13:17) und, nach Hinzufügung
von 7, das
Verhältnis 98:112 = 14*(7:8). Ohne die 5 haben die 7 Primzahlen
den Durchschnitt 13. Es ergibt sich
Teilbarkeit durch 13 durch die Additionen 7+19 = 26 und (1+11+17)+23 = 29+23 = 52. sowie
Teilbarkeit durch 7 durch 1+13 = 14; 11+17 = 28; 19+23 = 42.
Rechnet man für die Zahlen 1-24 die Primzahlsumme 91+10 = 101 und für die Zahlen 1-30 die Primzahlsumme 101+29 = 130, ergibt sich für beide Zahlenreihen 231 = 21*11. Die FS beider
Zahlenreihe ist 210+294
= 504, was das Verhältnis 231:273 = 21*(11:13) ermöglicht.
Für die Zahlenreihe 1-36 mit der FS 390 errechnet sich als
Primzahlsumme (91+5)+29+31
= 156. Daraus ergibt sich das
Verhältnis 156:234 =
78*(2:3) der Primzahlen zur übrigen FS. Fügt man 3 statt 5 hinzu, erhält man 154 = 14*11. Da die ZS+FS 1056 durch 11 teilbar ist, ergibt sich ein ZS+FS-Verhältnis der Primzahlen
zu den übrigen Zahlen von 308:748 = 44*(7:17).
Fügt man die Zahlenreihe 1-24 hinzu, erhält man als
Primzahlsumme (91+10)+151 = 252. Die Gesamt-ZS 966 ist
durch 42 teilbar, daher ist das ZS-Verhältnis der 22 Primzahlen
zu den 38 übrigen Zahlen 42*(6:17). Die Gesamt-FS ist 600, das
Verhältnis der Primzahlen-FS zur übrigen FS 252:348 =
12*(21:29).
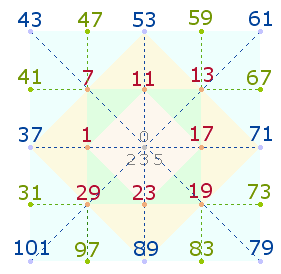
10. Der Rahmen des Basisquadrats mit Achsenkreuz
besteht aus 8 Punkten. Mit jedem weiteren Quadratrahmen kommen 8 Punkte hinzu. Es bietet sich daher an, die 8 Primzahlpositionen je 30
Zahlen auf konzentrischen Quadratrahmen anzuordnen:
|
|
Die Gesamtsumme der 24 Primzahlen in den zwei Quadratrahmen beträgt 120+1032 = 1152 = 24*48. Der Durchschnittswert der 24 Primzahlen ist demnach 48, also 2*(11+13) als geometrische Elemente zur Oktaederbildung.
Beide Summen sind durch 24 teilbar, das Verhältnis beträgt demnach 24*(5:43).
Die Summe der 8 Zahlen, die bei jedem
weiteren Quadrat erneut hinzukommen, beträgt 498 = 6*83, die ZS der vier
Achsen 654= 6*109 = FW 114 =
6*19. Sowohl 109 als auch 19 läßt sich als Summe 10+9 verstehen. 10+9 bedeutet, auf eine Tetraktys bezogen, 10 Punkte und 9 Dreiecksflächen. Die Tetraktys kann man von jeder
der 6 Ecken des Hexagramms gesehen werden.
Die Summe der anderen 8 Zahlen des äußeren Quadrats beträgt 534 = 6*89.
Fügt man dieser Summe und der Restsumme die LIBERO-Zahlen 2+3 und 5 hinzu, ist das Verhältnis 539:623 = 7*(77:89).
11. Erhöht man die Summe 654 durch die drei LIBERO-Zahlen 2 3 5 auf 664, sind die Faktoren 8*83. Das Verhältnis der nun 8:19 Zahlen ist demnach 498:664 = 2*83*(3:4)
= 166*(3:4). Die Einzelziffern der Zahl 166 sind zu verstehen als 1+6 hexagonale Punkte + 6 Erweiterungspunkte. 7:6 Punkte des Hexagramms bedeuten das Kreisflächenverhältnis 1:2. Die Zahl 83 stellt die
Numerierungssumme 28+55 der Zahlen 1-7 und 1-10 dar. 7:10 Punkte des Hexagons und der Tetraktys geben das
Kreisflächenverhältnis 1:3 wieder: Die Zahl 166 bezieht sich daher auf zwei Tetraktys. In
Kombination werden durch 166 3+4 Flächeneinheiten repräsentiert.
Die Addition der Summe 498 und der Summe 68 der Eckpunktzahlen des inneren Quadrats ergibt 566, die übrige Summe beträgt 586. Durch LIBERO-Hinzufügung von 8 und 2 kommt das Verhältnis 574:588 = 14*(41:42) zustande.
12. Es scheint nach dem bisherigen Befund, daß die Anordnung
der Primzahlen in konzentrischen Quadraten ein ontologisches Ordnungsmodell
darstellt. Ordnung in diesem Sinn ist nicht in Regeln und festen
Gesetzmäßigkeiten zu fassen, sondern zeigt sich in unendlich vielen Variationen
göttlicher Weisheit. Diese Ordnung kann an einzelnen auffälligen Merkmalen
erkannt werden, bildet aber in sich ein durchgängig vernetztes Sinngefüge, dem
bis in letzte Verästelungen nachgegangen werden könnte; nichts im Zahlensystem ist ohne Bedeutung. Um
jeweilige Ordnungselemente eines quadratischen Zuwachses erkennen zu können,
bedarf es Erfahrung, Geduld, Zeit und – unerläßlich – göttliche Erleuchtung.
Die Quadrate sind unendlich erweiterbar, aber stets auch auf ihr Zentrum
bezogen. Die grenzenlose Ausdehnung der Zahlen wird durch Primzahlfaktoren und
Zahlenverhältnisse auf ihr Zentrum zurückbezogen.
Nach dem christlichen
Glaubensbekenntnis ist Gott der Schöpfer der sichtbaren und unsichtbaren Welt. Die Ordnung der Zahlen gehört zur
letzteren.
13. Die doppelte Reihe von Primzahlen nach Plichta und Ullmann ergab bei 24 Primzahlen der ersten Hunderter-Einheit eine Gleichheit von 12+12 Zahlen und gleiche Summen mit der Zahl 44 als
Durchschnittswert. Dieses harmonische Ergebnis wird durch die Orientierung an
der ersten 100er-Einheit des Dezimalsystems ermöglicht. Wie sich die beiden
Reihen bei weiterer Fortsetzung verhalten, müßte untersucht werden. Eine
Überprüfung der Primzahlen von 1-1000 ergibt für die 1–7 Reihe 81 und für die 5–11 Reihe 86 Primzahlen mit der Differenz 39454-36669 = 2785. Die Summe 76123 beider
Reihen ist eine Primzahl.
Das 30-er Muster
erhält eine Bestätigung, wenn die Primzahlen der beiden äußeren Reihen addiert
und mit der Summe der mittleren Reihe ins Verhältnis gesetzt werden: 19957+18463+10 = 38430; 38430:37698
= 6*61*(105:103). Die LIBERO-Zahlen 2 3 5 erbringen einzeln kein befriedigendes Ergebnis, daher sind sie in ihrer
Summe anzuführen. Die FS der vier Zahlen ist eine Zehnerzahl: 2858+536+169+7 = 3570 = 210*17 = FW 17+17. 210 ist sowohl ZS der Zahlen 1-20 als auch FS der Zahlen 1-24. Zweimal 17 weist
besonders auf die Elemente von zwei Oktaederhälften hin.
Erstellt: 4.8.2003
Erweitert: Juni 2016