Zyklische Zahlen
(I)
A. Wesen und Arten
I.Einleitung
II. Eigenschaften von zyklischen Zahlen
III.
Ausgangspunkt von Primzahlen
IV. Zyklische
Zahlen 2. und höherer Ordnung
B. Definition und Einordnung der Zahlen 1, 2 u.5
siehe auch: Zwei Primzahlmuster
I.Einleitung
Alle Gesetze der Mathematik haben
ihren letzten Sinnbezug in der unendlichen Weisheit des dreieinen Gottes. Viele
Gesetze kann der menschliche Geist erkennen, erklären und beweisen, viele andere
aber übersteigen seine Erkenntnisfähigkeit. Im Folgenden werde ich eine Reihe
von Gesetzmäßigkeiten beschreiben und – soweit es mir möglich ist – begründen.
Als Wissensgrundlage dient mir Martin Gardner, Mathematischer Zirkus, Ullstein 1988, S.124
ff.
II.
Eigenschaften von zyklischen Zahlen
1.
Eine
zyklische Zahl ist eine Primzahl n,
deren Kehrwert 1/n
eine periodische Zahlenreihe von n-1 ergibt. Das bedeutet, daß alle Zehnerzahlen bis (n-1)*10 gemäß dem jeweiligen Teilungsrest
(Rest) durchlaufen werden, bis die letzte 10-er Zahl den Rest 1 ergibt, der mit einer weiteren 10 die nächste Periode eröffnet:
|
n=7 |
R |
n-1=6 |
|
|||||
|
10n-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Rest*10 |
1 |
10 |
30 |
20 |
60 |
40 |
50 |
10 |
|
Rest |
1 |
3 |
2 |
6 |
4 |
5 |
1 |
|
|
Rest*10/7 |
(0,) |
1 |
4 |
2 |
8 |
5 |
7 |
|
Multipliziert man die ermittelte
Periodik einer zyklischen Zahl (hier 7) mit 2 bis n-1, bleibt die Reihenfolge der Zahlen erhalten, z.B. 142857*3 = 428571. Dabei zeigt die Zehnerstelle des Restes*10 den
Multiplikationsfaktor an, der die dazugehörige Periodikziffer an den Anfang des
Multiplikationsergebnisses setzt (hier 3).
Zyklische Zahlen im eigentlichen
Sinn bilden einen Kehrwert mit einem einzigen Zyklus gleicher Zahlen. Alle anderen
Primzahlen bilden Kehrwerte mit zwei und mehr Zyklen. Diese werden weiter unten
behandelt.
2.
Die Periode einer zyklischen Zahl y besteht immer
aus einer geraden Stellenzahl sz= y-1. Teilt man die Stellenzahl in zwei Hälften, ergibt
die Addition zweier paralleler Zahlen jeweils 9, z.B. 1+8, während sich die Rest-Zahlen zu jeweils n=7 ergänzen, z.B. 3+4. Setzt man beide Hälften
untereinander, erhält man also 999 bzw. 777:
857
999
III.
Ausgangspunkt von Primzahlen
1.
Der Vorgang,
um die Periodik einer Primzahl (PZ) zu ermitteln, ist stets der gleiche: Die Zahl 1, durch die eine PZ n zu Anfang
geteilt wird, ist als Rest einer Teilung anzusehen. Die Periodik ist abgeschlossen, wenn die
Teilung des vorletzten Restes*10 den
Rest 1 übrig läßt. Zieht man 1 von 10a ab, erhält man eine Zahlenfolge zf von a-1 Neunen. Das bedeutet, daß jede PZ
>5
als Faktor in einer Zahlenfolge von Einsen enthalten ist. Wenn man z.B für die Zahl 41 die 5-stellige Periode 02439 ermittelt, dann ist sie durch
ebenso viele Einsen
teilbar: 11111/41
= 271. Natürlich hat
dann auch die Zahl 271
eine Periodik aus 5
Stellen, durch die wiederum 41
teilbar ist: 00369 = 9*41. Die teilbare Stellenzahl einer zyklischen Zahl ist um einen Zähler
geringer als die Zahl, für die Zahl 7 also 111.111. Man kann auch so definieren: Hat ein Primzahlfaktor in einer Zahl
aus n
Einsen den Wert n-1, ist sie eine zyklische Zahl.
2.
Besteht
eine Zahlenfolge zf*1
aus einer geraden Stellenzahl g,
z.B. 1111, ist die ganze Zahl durch die
Hälfte der Stellenzahl teilbar (111111/111). Das Ergebnis ist dann immer eine Eins am Anfang und am Ende und dazwischen g/2-1 Nullen (1001). Verdoppelt man die Stellenzahl einer solchen Zahl a und zieht eine Stelle ab, erhält man
die Stellenzahl sz als
potentiellen Faktor einer zyklischen Zahl y, z.B. a=1001; sz(y)=2*4-1=7; 1001:7 = 11*13. Auch die Zahl 13 hat demnach eine Periodik von 6 Stellen.
Umgekehrt, wenn man wissen will, ob eine PZ n zyklisch ist, ermittelt man die Stellenzahl (sz+1)/2 , versieht die erste und letzte Stelle mit einer 1 und die übrigen mit Nullen und
teilt n jeweils durch Rest*10. Wenn
die letzte Rest*10+1 durch n ohne Rest teilbar ist, ist PZ n
zyklisch. Die zyklische PZ 47 z.B. ergibt 24 Stellen.
3.
Bildet
man von einer zweistelligen Zahl die Umkehrung, so ist das Additionsergebnis
beider Zahlen durch 11
teilbar: z.B. 13+31 = 44 = 4*11. Ebenso ist eine 4-stellige Zahl durch 11 teilbar, wenn die Addition der
ersten und letzten beiden Stellen durch 11 teilbar ist, z.B. 2761 = 11*251. Analoge Teilbarkeit gilt für alle weiteren
geraden Stellenzahlen. Da nun jeder Kehrwert 1/n von einer Neunerreihe her ermittelt wird, müssen
beide Hälften einer geraden Periodik wieder eine 9-er Reihe bilden, d.h. zwei Parallelzahlen
müssen sich zu jeweils 9
ergänzen.
4.
Nach
Martin
Gardner beträgt das
Verhältnis der zyklischen Zahlen zu den übrigen Primzahlen 3:5. Ein wesentlicher Grund hierfür
ist, daß die Zahl, in der eine zyklische Zahl enthalten ist, um die Faktoren
der Hälfte der Stellenzahl vermindert ist.
|
2 |
11= 11 |
|
3 |
101= 101 |
|
4 |
1001= 7*
11* 13 |
|
5 |
10001= 73* 137 |
|
6 |
100001= 11* 9091 |
|
7 |
1000001= 101* 9901 |
|
8 |
10000001= 11* 909091 |
|
9 |
100000001= 17* 5882353 |
|
10 |
1000000001= 7* 11* 13* 19* 52579 |
|
11 |
10000000001= 101* 3541* 27961 |
|
12 |
100000000001= 11* 11*
23* 4093* 8779 |
|
13 |
1000000000001= 73* 137* 99990001 |
|
14 |
10000000000001= 11* 859* 1058313049 |
|
15 |
100000000000001=29*101*281*121499449 |
|
16 |
1000000000000001=7*11*13*211*241*2161*9091 |
Die Ausgangsfaktoren (11, 101 usw.) wiederholen sich im Intervall ihrer Stellenzahl sz, z.B. 7, sz=6: 4+6=10. Die gelb unterlegten Zahlen sind zyklische
Zahlen, sie ergeben sich aus sz+(sz-1).
|
1 |
1= 1 |
|
3 |
111= 3* 37 |
|
5 |
11111= 41*
271 |
|
7 |
1111111= 239* 4649 |
|
9 |
111-111-111= 3* 3* 37* 333667 |
|
11 |
11111111111= 21649* 513239 |
|
13 |
1111111111111= 53* 79* 265371653 |
|
15 |
11111-11111-11111= 3*31*37*41*271*2906161 |
Faktoren von Zahlen aus ungeraden Folgen
von Einsen wiederholen sich ebenfalls entsprechend der
Teilbarkeit dieser Folgen durch jeweils niedrigere Primzahlen (3, 5, 7 usw.).
IV.
Zyklische Zahlen 2. und höherer Ordnung
1.
Multipliziert
man den Kehrwert (bzw. die Periode p) einer zyklischen Zahl n (im eigentlichen Sinne) mit der Zahl n selbst, erhält man eine Folge von
Neunen, z.B. 1/7 = 0,142857*7 = 0,999999. Die Zahlen der Periode 1*p bleiben also in zyklischer Reihenfolge erhalten,
wenn man sie mit 2 bis n-1
multipliziert. Die Addition der Zahlen von 1 bis n-1 beträgt n*(n-1)/2, für die Zahl 7 als 7*3 = 21.
2.
Eine
zyklische Zahl n im
eigentlichen Sinne ist von 1 bis n-1 multiplizierbar und hat die
gleiche Stellenzahl
(sz) n-1. Eine solche Zahl bezeichnet man als zyklische Zahl
n-1/n-1 = 1. (erster) Ordnung (O).
3.
Alle
übrigen Primzahlen außer 1, 2, 5 bilden ein ganzzahliges Teilungsergebnis n-1/sz, das als nte Ordnung gilt. Die Periode der Zahl 13 z.B. hat – wie die der Zahl 7 – 6 Stellen. n-1/sz = 12/6 =
2. Ordnung. Die kleinste Zahl 2. Ordnung ist 3 (2/1). Der Ordnungszahl entspricht die Zahl der zyklischen
Zahlenreihen.
4.
Die
Addition der Multiplikationszahlen (m) einer zyklischen Reihe ergibt immer ein Mehrfaches (n-1)/(2*O) der Primzahl
n, für die Zahl 13 beträgt der Mehrfachfaktor f 12/(2*2) = 3, daher 3*13 = 39:
|
1.Reihe |
076923 |
769230 |
692307 |
923076 |
230769 |
307692 |
|
|
m |
1 |
10 |
9 |
12 |
3 |
4 |
39 |
|
2.Reihe |
153846 |
538461 |
384615 |
846153 |
461538 |
615384 |
|
|
m |
2 |
7 |
5 |
11 |
6 |
8 |
39 |
Wenn f = 2,5 wie bei der Zahl 41: 40/(2*8), ergeben die einen Reihen n*2, die anderen n*3:
|
Reihe |
|
|
|
|
|
|
|
1 |
1 |
10 |
16 |
18 |
37 |
82 |
|
2 |
2 |
20 |
32 |
33 |
36 |
123 |
|
3 |
3 |
7 |
13 |
29 |
30 |
82 |
|
4 |
4 |
23 |
25 |
31 |
40 |
123 |
|
5 |
5 |
8 |
9 |
21 |
39 |
82 |
|
6 |
6 |
14 |
17 |
19 |
26 |
82 |
|
7 |
11 |
12 |
28 |
34 |
38 |
123 |
|
8 |
15 |
22 |
24 |
27 |
35 |
123 |
|
|
47 |
116 |
164 |
212 |
281 |
820 |
Die Multiplikationszahlen
sind hier nicht nach ihrer zyklischen Abfolge, sondern linear aufsteigend
eingetragen. Die senkrechten Summen betragen in symmetrischer Ergänzung jeweils
4*41 je Spalte.
5.
Anhand
der Zahl 41 soll eine Neudefinition aller Primzahlen hinsichtlich ihrer zyklischen
Struktur erarbeitet werden. Für die Ermittlung der 5-stelligen Periode der Zahl
41 folgen nach der 1 fünf
Nullen: 1|00000. Die 5. Null ergibt den Rest 1, worauf mit der 6. Null eine neue
Periode beginnt. Denkt man sich eine Entsprechung von Zahl und Stellenzahl,
folgen nach der 1 8*5 Nullen, denen acht Perioden
entsprechen. Die Zahl 41 ist nach Abzug des Restes 1 in einer Folge von 41-1 = 40 Neunen enthalten, deren Teilung durch 9 in 40 Einsen
verwandelt wird. Die Neudefinition lautet also: Teilt man den Wert
n-1 einer Primzahl n
durch die Stellenzahl ihrer Periode sz,
erhält man ihre zyklische Größenordnung.
6.
Nach
den zyklischen Zahlen erster Ordnung sind die der zweiten Ordnung die weitaus
zahlreichsten. Ohne die Zahlen 1,2,5 gibt es bis zur Zahl 100.000 insgesamt 9590 zyklische Zahlen (Primzahlen),
davon 3617 (38%) erster Ordnung, 2684 (28%) zweiter Ordnung und 3289 (34%) höherer Ordnung.
Der Grund für die hohe Zahl der
zyklischen Zahlen 2. Ordnung liegt zunächst in der Bedeutung der Gleichung
1+2=3. Dann aber gehen beide Ordnungen auf Zahlen zurück, deren Stellenzahl
eine Konstitutive der entsprechenden Primzahl darstellt. Die höhere Konstitutive der Zahl 7 z.B. ist 4, was den 4 Stellen der Zahl 1001 entspricht, durch die 7 teilbar ist. Eine zyklische Zahl
2. Ordnung n ist in einer Folge von (n-1)/2 Einsen enthalten. Die Zahl 13 mit einer 6-stelligen Periode ist also durch 111.111 teilbar. Die Zahl 6 bildet die untere Konstitutivzahl von 13.
Die Zahl 7 ist die höhere Konstitutive der
Zahl 13. Beide sind – entsprechend ihrer
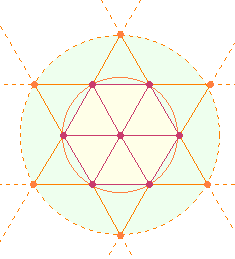
6-stelligen Periode – durch 111.111 teilbar. Ihre Bedeutung zeigt sich im Doppelkreis des Tetraktyssterns, der aus 7+6 = 13 Punkten besteht:
|
|
Setzt man die jeweils 6-stellige
Periode in Beziehung zu den jeweils 6 Kreislinienpunkten, ergibt sich eine
Entsprechung zwischen den zyklischen Ordnungszahlen 1 (7)und 2 (13) und der Flächengröße 1 des inneren Kreises und der Flächengröße 2 des äußeren Kreisrings.
Erstellt: Januar 2006