64 Komplementärzahlen auf Würfel und Oktaeder

I. Vorbemerkung

II. Verteilung auf zwei Würfel

III. 32 Würfel

IV. Würfel und Oktaeder

V. Verteilung auf 2 Oktaeder

VI. Gemeinsamkeit der Zahlenmodelle

I. Vorbemerkung

WÜRFEL und OKTAEDER haben die Zahl von 26 Elementen gemeinsam, indem es zwischen den Ecken und Flächen einen Tausch gibt: Der Würfel hat 8 Ecken und 6 Flächen, der Oktaeder 6 Ecken und 8 Flächen.

Die Grundlage für den Oktaeder ist das Hexagramm mit drei Doppelrauten. Zwei gekreuzte Doppelrauten können zu einem Oktaeder zusammengefügt werden. Die 6 Flächen der drei Doppelrauten passsen für den Würfel, die 8 Flächen des Quadrats der 64 Komplementärzahlen für den Oktaeder. Letzterer benötigt freilich gleichseitige Dreiecke, ersterer Quadrate. In einem höheren Sinn mag allerdings eine gegenseitige Austauschsituation bestehen, insofern auf diese Weise überzählige Flächen entfallen.

Am Ende meiner Überlegungen halte ich die Aufteilung der 8 Rautenquadrate auf zwei Oktaeder statt auf zwei Würfel für die bessere Lösung.

II. Verteilung auf zwei Würfel

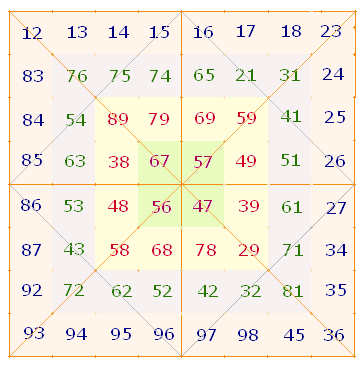
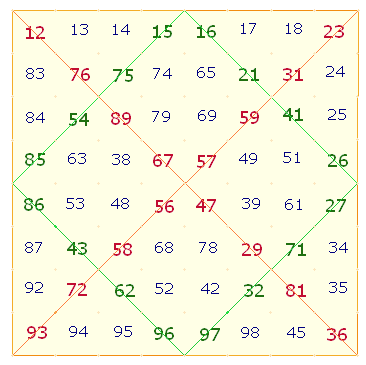
1. Die Ausführungen des vorhergehenden Kapitels haben gezeigt, daß die Anordnung der 64 Komplementärzahlen in einem Quadrat von quadratischen Feldern wesentliche Relevanz besitzt. Die einzelnen Zahlenergebnisse verweisen hauptsächlich auf die Bedeutungen des Hexagramms und seiner zwei konzentrischen Kreise. Doch auch auf das Quadrat selbst bezieht sich eine Reihe von Zahlen. Ich werde nur einige Ergebnisse interpretieren:

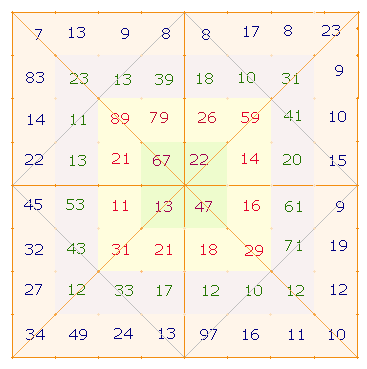
Die rechte Grafik enthält die Faktorenwerte (FW) der linken Zahlen.

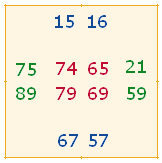
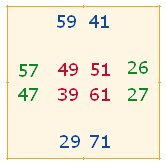
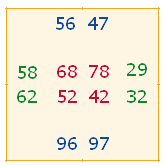
2. Analog zur Bildung eines Oktaeders aus zwei Doppelrauten des Hexagramms lassen sich die sechs Seiten eines Würfels aus dem vorliegenden 9x9 Punktequadrat mit 64 quadratischen Feldern konstruieren. Dies ist möglich, wenn man je zwei horizontale und vertikale Halbquadrate zu vier äußeren Quadraten zusammensetzt. Mit den inneren zusammenhängenden Rautenquadraten erhält man so acht Quadrate. Jedes Quadrat enthält 12 Zahlen, deren Zahlensummen (ZS) und Faktorensummen (FS) in den nächsten zwei Tabellen angegeben sind:

horizontal		vertikal
oben	unten	links	rechts
564	757	717	515	2553
289	326	238	253	1106
853	1083	955	768	3659
2553 = 69*37

Die vier zusammenhängenden Rautenquadrate der Mitte ergeben:

links	rechts	oben	unten
740	557	686	717	2700
419	404	438	341	1602
1159	961	1124	1058	4302
4302 = 18*239
1602:2700 = 18*(89:150)

Die Gesamtsummen der 8 Quadrate betragen 2553+2700 = 5253 = 3*17*103, 1106+1602 = 2708 = 4*677 und 3659+4302 = 7961 = 19*419.

3. Den 8 Quadraten stehen nur 6 Würfelseiten gegenüber, weswegen zwei Würfel benötigt werden, um alle Zahlen einzutragen. Es sind also die Zahlen von jeweils zwei Quadraten auszulassen. Nach welchen Kriterien soll man vorgehen?

Von jeder Gruppe ein Quadrat auszulassen, erscheint die sinnvollste Lösung für zwei Würfel. Bei der Suche danach kommen zwei Umstände zu Hilfe: Erstens, die ZS eines Dreierpaares erweitert die Teilbarkeit durch 37, und seihne ZS+FS ist durch 19 teilbar:

außen			sm	innen			sm	GS
564	757	717	2038	740	686	717	2143	4181
289	326	238	853	419	438	341	1198	2051
853	1083	955	2891	1159	1124	1058	3341	6232
4181 = 113*37; 6232 = 8*41*19

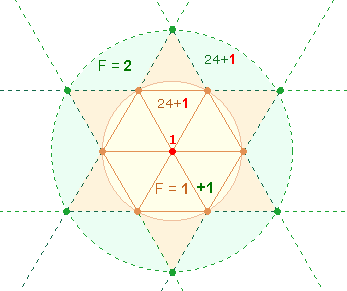
Die Gesamt-ZS 4181 weist in den Einzelziffern auf 4+1 und 8+1 Durchmesserelemente des hexagonalen Kreises und des erweiterten zweiten Kreises in der Doppelraute hin:

Die Zahl 1 bezieht sich jeweils auf den Mittelpunkt. Die Zahl 113 kann sich sowohl auf die Elemente zweier geometrischer Figuren der DR als auch auf die Numerierungssumme der vier Achsen eines erweiterten Quadrats beziehen. Aus 37 Elementen und 3+7 Punkten besteht eine Tetraktys.

4. Der zweite Umstand besteht darin, daß von jeder Gruppe die ZS+FS eines Quadrats durch 19 teilbar ist, was auch für die beiden ausgelassenen Quadrate gilt, die in der folgenden Tabelle links stehen:

v-re	Mi-re	sm	h-u	Mi-li	sm	GS
515	557	1072	757	740	1497	2569
253	404	657	326	419	745	1402
768	961	1729	1083	1159	2242	3971
1729:2242 = 19*(91:118) = 19*209
3971 = 11*19²

Die Faktoren der ZS+FS 1083 sind 3*19², das Verhältnis von 1:3 Summen ist daher 19²*(3:8).

5. In paarweiser Zuordnung sind die ZS+FS der anderen vier Quadrate durch 21 teilbar:

v-li	Mi-ob	sm	h-ob	Mi-un	sm	GS
717	686	1403	564	717	1281	2684
238	438	676	289	341	630	1306
955	1124	2079	853	1058	1911	3990
2079:1911 = 21*(99:91) = 21*190
3990 = 19*210

Am auffälligsten ist das Verhältnis der Gesamtsummen 3971:3990 = 19*(209:210).

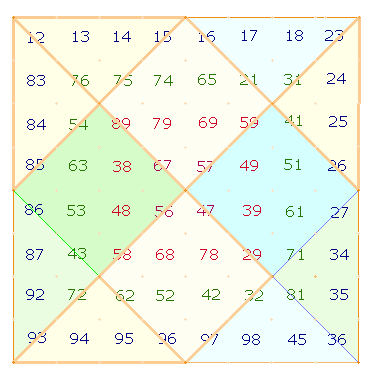
Die Aufteilung der zwei Vierergruppen zeigt die folgende Grafik:

Die zweimal zwei durch 19 teilbaren Quadrate sind blau und grün gekennzeichnet, die übrigen vier gelb. Man erkennt, daß die inneren Quadrate ein horizontal-vertikales Achenkreuz bilden und die äußeren Quadrate einander diagonal zugeordnet sind.

6. Die jeweils durch 19 teilbaren Quadrate wird man der Ober- und Unterseite des Würfels zuweisen, die übrigen vier rundum anordnen:

	1083				961
955	853	1124	1058	955	853	1124	1058
	1159				768
6232 = 328*19				5719 = 301*19
6232+5719 = 11951 = 17*19*37 = FW 36+37 = 73

7. Die Faktoren und Primzahlen 19*419 (FW 438) der Gesamt-ZS+FS 7961 sind in folgender Weise auf den Tetraktysstern (das Hexagramm) bezogen:

– Die Einzelziffern des FW 438 bezeichnen die Rahmenelemente der Doppelraute (DR): 4+3 Punkte und 8 Linien. Die 21 Elemente der DR lassen sich in 7*3 aufteilen:

Der FW von 438 ist 78 = 3*26. 6 DR ergeben aus drei DR-Kreuzen drei Oktaeder, die jeweils aus 26 Elementen bestehen.

– Das Produkt 6*73 gibt 6-mal 7+3 Punkte der Tetraktys wieder, wenn die Numerierung jeweils von den 6 äußeren Eckpunkten ausgeht.

419 ist als 4*19 zu verstehen und auf zwei Tetraktys beziehbar. Die FS 419 des linken zentralen Rautenquadrats gibt dazu einen Hinweis, da sich so das Verhältnis 419*(1:18) ergibt. Die Zahl 1 steht für den Mittelpunkt einer Tetraktys, die Zahl 18 für ihre Rahmenelemente aus 9 Punkten und 9 Linien. Eine zweite Zählung erfaßt 10 Punkte und 9 Dreiecke. Aber auch an 9 Durchmesserelemente und zweimal 5 Radialelemente der DR ist zu denken: Im Hinblick auf die Oktaederbildung ergeben sich vier Zickzacklinien, die so gezählt werden können. Die Buchstabenentsprechung für 19 ist T, das im SATOR-Quadrat viermal enthalten ist.

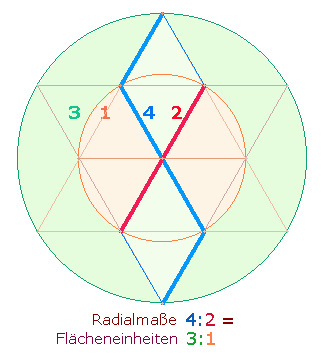
19*419 kann somit auch 5*19 = 95 bedeuten. 9:5 Durchmesserlemente geben 3:1 Flächeneinheiten der beiden Tetraktyskreise wieder. Bei umlaufender Numerierung der DR-Punkte stehen sich 5 und 19 gegenüber.

Die Einzelziffern der Zahl 419 und ihrer 5 Umkehrungen stellen Quadrate der Zahlen 1-3 dar und haben somit trinitarische Bedeutung.

8. Durch die Aufteilung der 64 Komplementärzahlen in 8 Rautenquadrate werden 2x16 der Zahlen auf den Diagonallinien (rot) und den Rahmenlinien des großen Rautenquadrats (grün) doppelt erfaßt:

Die ZS+FS der zu verdoppelnden Zahlen sind:

D-L	R-L	sm
886	847	1733
509	449	958
1395	1296	2691
2691 = 9*13*23
1296 = 16*81

Die 16 Zahlen der Rahmenlinien haben den durchschnittlichen ZW+FW 81. Das Verhältnis der beiden ZS+FS 1395:1296 ist 9*(155:144). Die Differenz zur Gesamt-ZS 3520 und FS 1750 beträgt 1787 (PZ) und 792 = 72*11. Die erweiterten Summen sind 5253+2708 = 7961.

9. Nach Zusammensetzung der Halbquadrate umschließen 8 Linienzahlen eines Rautenquadrats je 4 quadratisch angeordnete Mittelzahlen. Die ZS+FS der 4x4 Zahlen des großen Rautenquadrats zeigen, daß je zwei diagonal liegende Quadrate ein Verhältnis bilden:

ob	re	sm	li	unt	sm	GS
287	200	487	202	240	442	929
162	111	273	98	68	166	439
449	311	760	300	308	608	1368
760:608 = 8*19*(5:4) = 72*19

Das ZS+FS-Verhältnis der 16 Mittelzahlen zu den übrigen 80 Zahlen beträgt 19*(72:347).

Die Summen 929 und 439 sind Primzahlen, erst ihre Addition ermöglicht das Zahlenverhältnis. Der ZW+FW je Zahl beträgt in der rechten Hälfte 95, in der linken 76.

Die ZS+FS der zusammengesetzten Quadrate sind:

v-li	h-ob	sm	v-re	h-unt	sm	GS
216	216	432	178	248	426	858
95	116	211	52	90	142	353
311	332	643	230	338	568	1211
432:426 = 6*(72:71) = 6*11*13
1211 = 7*173

Auch in dieser Gruppe ist eine diagonale Ausrichtung erkennbar. Erstaunlich sind die angrenzenden Konstitutivzahlen 72 und 71, ebenfalls zweimal dieselbe ZS 216, deren Faktoren 6³ auf die Dreidimensionalität des Würfels hinweisen.

Die Faktoren 6*11*13 sind auf die drei DR des Hexagramms zu beziehen, aus deren zwei geometrischen Figuren der Oktaeder zusammengesetzt ist. Die doppelte Zahl von DR ist erforderlich, wenn jede mit jeder sich zur Oktaederbildung verbindet.

Bemerkenswert ist die FS 792 = 72*11 aller 32 Zahlen, denn sie stellt eine Verbindung dar zwischen der ZS 858 = 78*11 der äußeren Quadrate und der ZS+FS 1368 = 72*19 der inneren. Die durchschnittliche FS je 4 Zahlen ist 99.

Die Unabhängigkeit der 8x4 Innenzahlen legt nahe, sie auf zwei Würfel zu verteilen. Zu vertauschen sind die durch 19 teilbaren ZS+FS-Paarungen 608 und 760. Analog dazu kann man auch die ZS allein verwenden. Die ZS+FS sowie die ZS der äußeren Quadrate bleiben unverändert:

au.	inn.		au.	inn.
1211	608	1819	858	487	1345
1211	760	1971	858	442	1300
		3790			2645
1819 = 17*107; 1971 = 27*73
2645 = 5*23*23

Die Summe 1819 bezieht sich auf 18 Linien und 10 Punkte + 9 Dreiecke der Tetraktys, der Faktor 73 auf deren 7 hexagonale und 3 Erweiterungspunkte. Die 37 Elemente der Tetraktys erscheinen wieder in der ZW/FW-Verrechnung:

			sm
ZS+FS	1819	1971	3790
FW	124	82	206
sm			3996
3996 = 12*9*37

Die Faktoren 12 und 9 bedeuten 3*4 Punkte und 3*3 Linien der drei Tetraktysseiten.

III. 32 Würfel

1. Die 8 Rautenquadrate lassen sich durch Drehung zu horizontal-vertikalen Quadraten verwandeln. Die ersten vier Quadrate sind dem großen Rautenquadrat entnommen, die nächsten vier aus zwei Halbquadraten zusammengesetzt. Die Anordnung der zweimal vier Quadrate ergibt sich aus einer Kippsituation nach links:

mo ml mr mu

ho vl hu vr

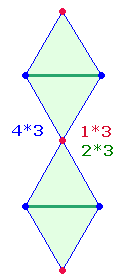
2. Jedes Quadrat enthält 12 Komplementärzahlen im vertikal und horizontal gleichen Muster 2:4+4:2, wodurch die Gesamtzahl auf 24 verdoppelt wird. Dem Verhältnis von 2:4/4:2 Radiallinien der beiden Tetraktyskreise entspricht das trinitarische Kreisflächenverhältnis 1:3/3:1:

Auch an 6*4 = 24 Punkte von zweimal drei Tetraktysseiten, die durch 18 Linien zu 42 Elementen vervollständigt werden, ist zu denken.

3. Durch den vertikalen und horizontalen Aspekt erhält man viermal 6 Zahlen, die vier Würfeln zugeordnet werden können. Man wird die Zahlen paarweise und entgegengesetzt anordnen.

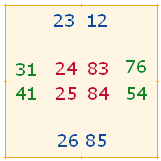
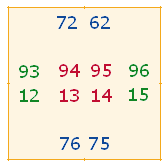
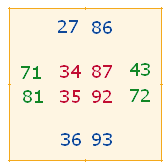
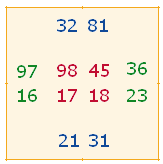
Ich beschränke mich auf die Darlegung des oberen mittleren Quadrats, des ersten der 8 angeführten Grafiken, und betrachte dabei alle 4Werte. Ich gehe horizontal von oben nach unten und vertikal von links nach rechts vor:

	ZS	FS	sm	FW1	FW2	sm	GS	FW
ob	266	96	362	28	13	41	403	44
unt	420	342	762	19	27	46	808	107
li	399	295	694	29	64	93	787	787
re	287	143	430	48	24	72	502	253
sm	1372	876	2248	124	128	252	2500	1191
403 = 13*31; 124:128 = 4*(31:32) = 252 = 12*21

Die ZS 1372 ist, wie bereits erwähnt, das Doppelte der Ausgangssumme 686 = 2*7³.

Erstaunlich ist die 4W-Summe 2500 = 50*50 = FW 12+12 = 24. Das Hexagon besteht aus 25 Elementen und ebenso der Erweiterungsbereich, wenn man für den äußeren Kreis einen weiteren Mittelpunkt zählt. Beide Bereiche enthalten 12 Linien:

In Beziehung zu den beiden Kreisen bedeutet 25+25 das Flächenverhältnis 1:3 bzw. 3:1. Dies zeigt sich auch in der ersten 4W-Summe 403 = 13*31. Die durchschnittliche 4W-Summe ist 625 = 25*25.

Das Umkehrprodukt 12*21 steht im Einklang mit der Ausgangssumme 686 = 2*7³, indem 3*4 = 12 Punkte der drei Tetraktysseiten durch 9 Linien zu 21 ergänzt werden.

4. Von Interesse sind auch die Würfelsummen und ihre FW. Jeweils 6 Zahlen werden nach ihrer konzentrischen Anordnung auf entgegengesetzten Würfelseiten eingesetzt, z.B. 74 65; 75 21, 15 16. Es gibt jeweils drei verschiedene Würfelsummen. Ich beschränke mich auf die drei Würfelreihen der 12 oberen horizontalen Zahlen:

	ZS	FW1	sm	FS	FW2	sm	GS
74 65 75 21	235	52	287	80	13	93	380
74 65 15 16	170	24	194	73	73	146	340
75 21 15 16	127	127	254	39	16	55	309
sm	532	203	735	192	102	294	1029
203:532 = 7*(29:76) = 7*105; 102:192 = 6*(17:32) = 6*49
294:735 = 7*7*(6:15) = 49*21 = 3*7³

Der Bezug des Ergebnisses 3*7³ zur ZS 686 = 2*7³ sowie die Zahlenverhältnisse stellen gewiß einen Glücksfall dar, aber es dürfte insgesamt eine innere Ordnung walten, die in ihrem ganzen Ausmaß erkennbar wird, wenn alle 32*6 Zahlenreihen berechnet sind.

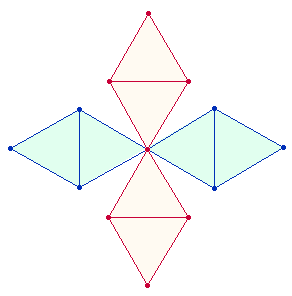
5. Jedes Einzelquadrat enthält, horizontal und vertikal, zwei Reihen von vier Zahlen, denen je vier Flächen von zwei Oktaederhälften entsprechen:

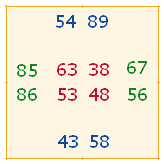
Auf diese Weise können 16 Oktaeder besetzt werden.

6. Die ZS folgender vier oberer und unterer Quadrate sind durch 17 teilbar und können den Flächen zwei Oktaederhälften zugeordnet werden:

ho	vl	Mo	vr	sm	Ml	hu	Mr	Mu	sm
564	717	686	515	2482	740	757	557	717	2771
2482:2771 = 17*(146:163)

Die FW der beiden Summen sind zusammen ebenfalls durch 17 teilbar: 17*2*73 > 92, 17*163 > 180; 92+180 = 272 = 16*17. Es ergibt sich so das Gesamtverhältnis 17*(16:309) = 17*325 = 25*13*17. 325 ist die Summe der Zahlen 1-25 mit 13 als Mittelpunktszahl. Sowohl 73 als auch 163 verweisen auf die 10 Punkte der Tetraktys.

IV. Würfel und Oktaeder

1. Die Außenseite eines Würfels besteht aus 6*4 Quadratpunkten, die des Oktaeders aus 8*3 Dreickspunkten. Gemeinsam ist beiden Körpern also die Zahl 24. Das Verhältnis von 6*8 zu 4*3 ist 1:4. 24 ist auch komplementär zur Zahl 86, die – in seltener Übereinstimmung mit ihrer Quersumme – die FS der Zahlen 1-14 ist. Die Einzelziffern von 24 stellen die 6 Flächen des Würfels dar.

In vertikaler Ausrichtung dominiert beim Würfel die horizontale Fläche, beim Oktaeder die Ecke (die Spitze, der Punkt), während den horizontalen Aspekt des Oktaeders die quadratische Mittelbasis bildet

2. Die Austauschsituation von Würfel und Oktaeder besteht darin, daß ein Quadrat aus 8 einzelnen Quadraten zu den 8 Flächen des Oktaeders paßt, die 6 RAUTEN des Hexagramms hingegen zu den Würfelflächen.

3. Im Hexagramm enthalten sind drei Doppelrauten (DR). Zwei gekreuzte Doppelrauten können zu einem Oktaeder zusammengefügt werden:

Dem Oktaeder gebührt ein gewisser Vorrang vor dem Würfel, insofern ersterer das Ergebnis einer dreiachsigen und zweiachsigen Ausgangsfigur darstellt, der Würfel jedoch nur aus Zweiachsigkeit hervorgeht.

4. Ein gerollter Würfel bleibt mit einer Oberseitenfläche liegen. Das erklärt seine Beliebtheit und Faszination als Spielwürfel. Die Würfelaugen sind auf gegenüberliegenden Seiten jeweils zur Summe 7 angeordnet: 1+6, 2+5, 3+4. Die Summe der Zahlen 1-6 beträgt also 21, aufgeteilt in 3*7.

Die Zahlen 7 und 3 prägen wesentlich auch den Tetraktysstern: Eine Tetraktysseite besteht aus 4 Punkten und 3 Linien, also 7 Elementen, woraus sich für zwei Tetraktys die Zahl von 42 Elementen ergibt. Eine ganze Tetraktys besteht ferner aus 37 Elementen, einer zweistelligen Zusammensetzung aus 3*7. Die Tetraktys geht schließlich hervor aus 7 hexagonalen und 3 Erweiterungspunkten.

Die Doppelraute besteht als ganze aus 21 Elementen, auf der Grundlage von 7 Punkten, zwei Doppelrauten aus 42 Elementen, um einen Oktaeder zu bilden.

Die erwähnte Vorrangstellung des Hexagramms als Ausgangsfigur des Oktaeders vor dem Würfel zeigt sich, wenn man zu den zweistelligen Zusammensetzungen 68, 86, 42, 24 die Faktorensummen (FS) hinzunimmt:

			sm			sm	GS
Zahl	68	86	154	42	24	66	220
FW	21	45	66	12	9	21	87
			220				307
66:154 = 22*(3:7); 33:54 = 3*(11:18)

Die FS 66 weist auf die Elemente von 6 Rauten hin, die Zahl 87 auf 8 Linien und 7 Punkte des DR-Rahmens sowie auf jeweils 29 Rahmenelemente von drei DR-Kreuzen hin, das Verhältnis 11:18 auf die Numerierungssumme des hexagonalen + des Erweiterungsdurchmessers:

Die Gesamtsumme 307 konzentriert die Berechnung wiederum auf die Ausgangszahlen 3 und 7.

5. Das Hexagramm besteht 13 Punkten, 24 Linien und 12 Dreiecken, zusammen 49 Elementen, die man der Reihe nach numerieren kann:

Die eingetragen Zahlen ergänzen sich spiegelbildlich zu 50, z.B. 2+48. Die 6 Rautenfiguren teilen miteinander den Mittelpunkt, 6 Punkte und 6 Linien des Hexagons. Zur einfachen Zählung der ZS 25*49 = 1225 kommt daher noch die ZS 300 für 6 Punkte und 6 Linien sowie 5*25 = 125 für den Mittelpunkt hinzu, zusammen ergibt sich 1650 = 150*11. Da eine Raute aus 11 Elementen besteht, entfällt konsequenterweise auf jedes Element die Summe 25.

Die Spiegelbildlichkeit der Hexagrammgestalt bewirkt, daß sich die ZS von zwei zusammengehörigen Rauten zu 50*11 = 550 ergänzen. Die folgende Zählung beginnt mit der Doppelraute in der Mitte und setzt sich links und rechts fort, jeweils zuerst die obere, dann die untere Raute:

	oben				unten
	Mi	li	re	sm	Mi	li	re	sm	GS
ZS	110	160	208	478	440	390	342	1172	1650
FW	18	15	21	54	22	23	27	72	126
126 = 6*21

Das Verhältnis der FW-Summen 54:72 ist 18*(3:4). Entsprechend der Anzahl der FW setzt sich die Gesamtsumme 126 aus 21*(1+2+3) zusammen. Wenn jede DR sich mit jeder verbindet, sind 6 DR erforderlich, um drei Oktaeder zu bilden.

Die ZS+FS 1650+126 = 1776 = 48*37 verweist wiederum auf die 37 Elemente der Tetraktys sowie auf 2*(11+13) Elemente zweier geometrischer Figuren, aus denen der Oktaeder besteht.

6. Die FS der Zahlen 1-49 beträgt 694 = 2*347. Die Primzahl 347 ist auf drei Tetraktysseiten zu beziehen, deren Elemente sich als 3*4 Punkte und 3*7 Elemente und somit als Umkehrsummen 12 und 21 darstellen lassen. Zu dieser Summe kommt noch 129 = 3*43 für die gemeinsamen 6 Punkte und 69 für 6 Linien sowie 50 für 5*25 des Mittelpunktes hinzu, zusammen 248 = 8*31 > FW 37. Das Verhältnis 3*(43:23) = 3*66 weist wieder auf die Elemente der 6 Rauten hin.

Die FS der 6 Rauten sind folgende:

	oben				unten
	Mi	li	re	sm	Mi	li	re	sm	GS
FS	72	104	117	293	246	202	201	649	942
FW	12	19	19	50	46	103	70	219	269
	84	123	136	343	292	305	271	868	1211
942 = 6*157; 343:868 = 7*(49:124) = 7*173
104:117 = 13*(8:9) = 13*17; 202+201 = 403 = 13*31

Die FS der zu drei DR vereinten sechs Rauten sind 72+246 = 6*(12:41) = 6*53 = 318; 104+202 = 2*(52:101) = 2*153 = 306; 117+201 = 3*(39:67) = 3*106 = 318. Das Verhältnis der drei Summen ist 6*(53:52:53). Bemerkenswert sind die benachbarten Zahlen 52 und 53, da die ZS der 8 Quadrate mit Komplementärzahlen 5253 beträgt.

-----------------

Auffällig ist die gleiche FS 318 für die mittlere und rechte DR. Die linke und die rechte DR bilden eine Einheit, indem die FS der oberen und unteren Rauten jeweils durch 13 teilbar sind.

Die Zahlenkombination 17 und 31 begegnen häufiger und sind erklärbar als ZS 21+10 und deren FW 10+7. Die Zahl 21 kann sich aus 3*7 Elementen der drei Tetraktysseiten zusammensetzen, die Zahl 10 sich auf die Anzahl der Tetraktyspunkte beziehen. 21*10 ist die Summe der Zahlen 1-20. Die FW 10 und 7 lassen sich als Punkte der Tetraktys und des Hexagons und als Kreisflächenverhältnis 3:1 verstehen. Das lateinische Wort HOMO – Mensch hat die ZS 48 und die FS 31, somit die Differenz 17 zwischen FS und ZS.

Die Zahl 246 läßt sich aufteilen in 24+6 und setzt sich dann aus den Komplementärzahlen 9+8+7 und 1+2+3 zusammen.

-----------------

7. Wenn man jeweils zwei der drei Summen 318, 306, 318 addiert, erhält man die drei unterschiedlichen Würfelsummen:

	sm	FW
318 306	624	24	648
318 318	636	60	696
306 318	624	24	648
sm	1884	108	1992
24:60:24 = 12*(2:5:2)

Das Verhältnis 2:5:2 spiegelt die Gliederung der 9 Durchmesserlemente des Tetraktyssterns wider sowie die Elemente einer Kreisteilung.

V. Ein Würfel, zwei Oktaeder

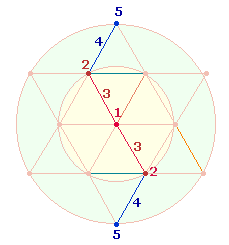
Während man sich die Umwandlung einer Raute, die aus zwei gleichseitigen Dreiecken besteht, in ein Quadrat vorstellen kann, so daß sich 6 Rauten den 6 Seiten eines Würfels zuordnen lassen, bleibt ein Rautenquadrat als zwei Dreiecke bestehen, so daß vier Rautenquadrate zu zwei Oktaedern werden. Tatsächlich zeigt sich ein überzeugendes ZS-Verhältnis, wenn man die vertikale Doppelraute des Komplementärquadrats und die zwei linken und rechten Dreiecke zu zwei Doppelrauten macht und in gleicher Weise mit den horizontalen Rautenteile verfährt:

vertikal		Mitte		sm	horizontal		Mitte		sm
links	rechts	oben	unten		oben	unten	links	rechts
717	515	686	717	2635	564	757	740	557	2618
2635:2618 = 17*(155:154) = 17*309

Die Zahl 17 stellt die Elemente einer Oktaederhälfte dar: 5 Ecken + 4 Flächen und 8 Kanten.

Erstellt: Dezember 2014

INHALT 2