Die Zahl 194
9+8 und 9+6 im Doppelrautenkreuz
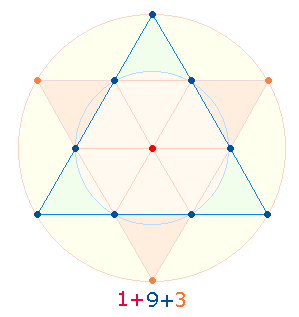
1. 194 folgt der Zahl 193, deren Einzelziffern die Punkteverteilung des Tetraktyssterns wiedergibt:
|
|
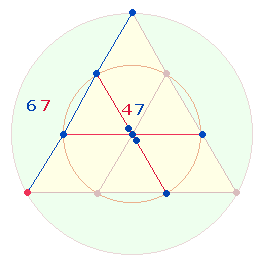
Damit der äußere Kreis gezogen werden kann muß der Mittelpunkt ein zweites Mal verwendet werden. Dadurch beträgt das Flächenverhältnis des äußeren Kreises zum inneren 3:1, bei einem Mittelpunkt wird nur der äußere Kreisring berücksichtigt, so daß sich das Flächenverhältnis 2:1 ergibt.
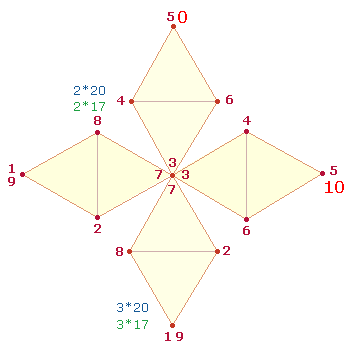
2. Dem SATOR-Quadrat liegt ein 1x1-Modell ohne Zehnerstellen zugrunde:
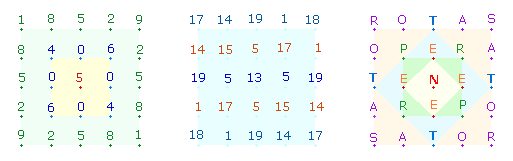
Die Summe der Zahlen beträgt 105, die Faktorenwerte (FW) 89, ergibt die ZS+FS 194.
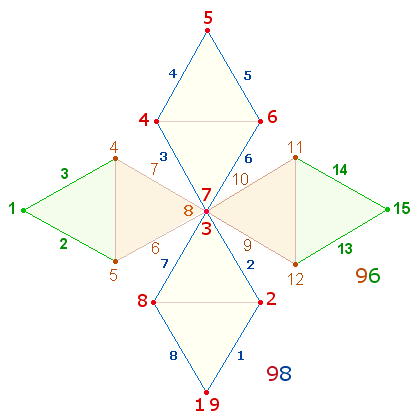
3. Für das Dezimalsystem wesentlich sind zwei numerierte Doppelrautenkreuze:
|
|
|
Die FW der Zahlensummen (ZS) und Faktorensummen (FS) ergeben 194:
|
|
1-9/1-10 |
23/24 |
|
|
|
|
|
ZS |
FS |
ZS |
FS |
sm |
|
ZS |
100 |
85 |
576 |
411 |
1172 |
|
FW |
14 |
22 |
18 |
140 |
194 |
|
1172+194 = 1366 = 2*683 |
|||||
4. Der Tetraktysstern besteht aus 25 Elementen des Hexagons und 24 Elementen seiner Erweiterung. Elemente sind Punkte, Linien und Flächen. Die 4Werte der 25 hexagonalen Elemente und der 49 Elemente des ganzen Hexagramms ergeben:
|
|
Hexagon |
|
Hexagramm |
|
|
||||
|
|
P |
L |
F |
sm |
P |
L |
F |
sm |
GS |
|
ZS |
7 |
12 |
6 |
25 |
13 |
24 |
12 |
49 |
74 |
|
FW |
7 |
7 |
5 |
19 |
13 |
9 |
7 |
29 |
48 |
|
|
|
|
|
44 |
|
|
|
78 |
122 |
Nun wird zu den ZS und den FS der beiden Kreisfiguren jeweils deren FW-Summe gestellt:
|
ZS |
FW1 |
sm |
FS |
FW2 |
sm |
GS |
|
25 |
10 |
35 |
19 |
19 |
38 |
73 |
|
49 |
14 |
63 |
29 |
29 |
58 |
121 |
|
74 |
24 |
98 |
48 |
48 |
96 |
194 |
98 und 96 sind die Konstitutivzahlen ihrer Summe 194.
5. Die Achsen des Hexagons bestehen aus jeweils 3 Punkten, also insgesamt 9. Zählt der Mittelpunkt nur einmal, sind es 7 Punkte. Hieraus ergibt sich eine Doppelzählung auch für die übrigen Elemente. Die Zahl von 25 Elementen vergrößert sich durch 2 weitere Mittelpunkte auf 27, sodaß die Doppelzählung 52 = 4*13 ergibt.
Durch die Erweiterung des Hexagons zum Hexagramm entstehen 6 Zickzacklinien aus je 5 Punkten und 4 Maßeinheiten (Linien), zusammen aus 9 Elementen, die man vom unteren zum oberen Punkt numerieren kann:
|
|
Einer Zickzacklinie entspricht eine spiegelsymmetrische zweite, wodurch eine Doppelraute (DR) zustande kommt. Diese zweite Zickzacklinie kann nun bis zum unteren Ausgangspunkt weiternumeriert werden. Mittelpunkt und Ausgangspunkt sind doppelt besetzt, sodaß die Numerierung mit 17 endet. In einfacher Zählung besteht also der DR-Rahmen aus 15 Elementen. Hinzu kommen weitere 6 Binnenelemente. Die Doppelzählung der ganzen DR ergibt somit (17+6)+(15+6) = 23+21 = 44 = 4*11.
Ein Oktaeder ist entweder durch 4 Rauten aus jeweils 11 Elementen oder 4 sanduhrförmigen Doppeldreieck aus 13 Elementen zusammensetzbar, oder doppelt im Zusammenwirken beider. Gemeinsam sind Hexagon und Doppelraute also jeweils 7 Punkte. Ein Doppeldreieck bildet den hexagonalen Anteil einer DR.
9+8
und 9+6 im Doppelrautenkreuz
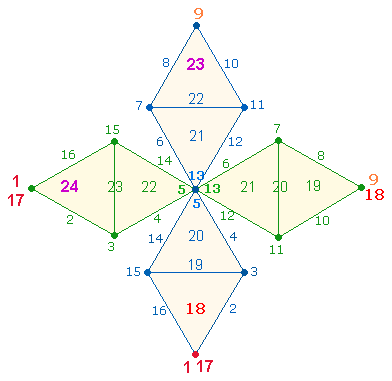
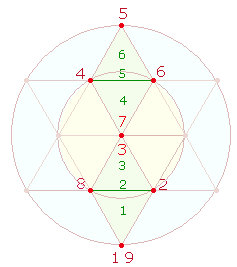
1. 98 und 96 können als Einzelziffern 9+8 und 9+6 folgendermaßen in zwei DR-Rahmen des DR-Kreuzes dargestellt werden:
|
|
In
der vertikalen DR sind
Punkte und Linien, jeweils von 1 beginnend,
in 8-förmiger Umfahrung numeriert, in der horizontalen DR werden
die 15 Elemente des DR-Rahmens von einem
Element zum Gegenelement (2 3), teils linear(3 4), teils in Zickzackform, von links nach rechts
besetzt. Den beiden Umläufen entsprechen 3+3
Kreisflächeneinheiten.
Die 4Werte der 4 Rauten sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
unten |
41 |
34 |
75 |
41 |
19 |
60 |
135 |
|
rechts |
84 |
61 |
145 |
14 |
61 |
75 |
220 |
|
|
125 |
95 |
220 |
55 |
80 |
135 |
355 |
|
links |
36 |
33 |
69 |
10 |
14 |
24 |
93 |
|
oben |
40 |
38 |
78 |
11 |
21 |
32 |
110 |
|
|
76 |
71 |
147 |
21 |
35 |
56 |
203 |
|
|
201 |
166 |
367 |
76 |
115 |
191 |
558 |
|
558 = 18*31 >39 = 3*13 |
|||||||
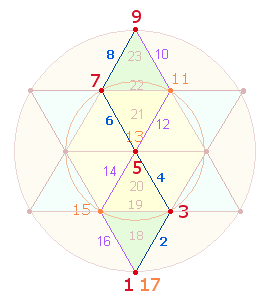
2. 9:6 bedeutet 9 Rahmenelemente: 5 Punkte + 4 Linien (hellbraune Füllung) des hexagonalen Bereichs und 2*3 Elemente des Erweiterungsbereichs. Letzterer gibt die doppelte Kreisfläche des hexagonalen Kreises wieder. In vierstelliger Zusammensetzung kommt die Zahl 3312 = 144*23 zustande. Die beiden Produktzahlen enthalten in ihren Einzelziffern 9 Elemente der Zickzacklinie und 5 Elemente der Kreisachse in der Bedeutung von 3:1 Kreisflächeneinheiten.
Das Verhältnis 9:6 = 3*(3:2) läßt sich dreimal an je einer Zickzacklinie ablesen 3 Punkte + 2 Linien des hexagonalen Bereichs und 3 Punkte + 2 Linien je halben Rautenrahmen, z.B. 1+4+8 + 3+7.
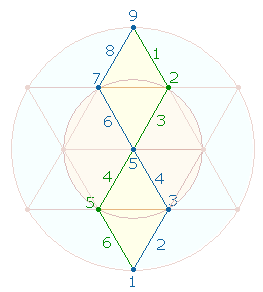
Es gibt zwei weitere Interpretationen von 9+6:
|
|
|
In der linken Grafik werden die Punkte schleifenförmig bis 9 und dann die Binnenelemente bis 6 numeriert. In der rechten Grafik wird eine Zickzacklinie ganz durchgezählt und die restlichen Rahmenelemente bis 6 ergänzt. Diese Sichtweise ist deswegen von besonderem Interesse, weil 6 der FW von 9 ist.
3. Die ZS und FS der beiden DR sowie ihrer FW sind:
|
|
1-9 |
1-8 |
|
FW |
|
|
ZS |
45 |
36 |
81 |
12 |
|
|
FS |
33 |
39 |
72 |
12 |
|
|
|
|
|
153 |
24 |
177 |
|
1-15 |
ZS |
|
120 |
14 |
|
|
|
FS |
|
94 |
49 |
|
|
|
|
|
214 |
63 |
277 |
|
GS |
|
|
367 |
87 |
454 |
|
454 = 2*227 |
|||||
Die
ZS der beiden DR beträgt
81+120 = 201 = 3*67 , die FS 166 =
2*83. Die ZS 201
nimmt bereits im Produkt 3*67 die ZS+FS 367 voraus. Die Einzelziffern der FS 166 geben
die 1+6 Punkte des Hexagons und die 6 Punkte der Erweiterung zum Hexagramm wieder. 83 ist die Summe der Zahlen 1-7 und 1-10 = 28+55.
Den 4W-Summen
177 und 277 entsprechen 15+16 Rahmenelemente zweier DR mit einem und zwei
Mittelpunkten.
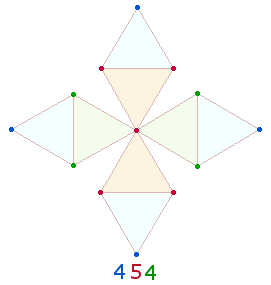
Die Einzelziffern der Gesamtsumme 454 sind auf die 13 Punkte eines DR-Kreuzes beziehbar:
|
|
227 ist eine Primzahl. Ihre Einzelziffern sind zu verstehen als 2+2 Dreiecksflächen der DR und 7 Punkte. In der Verdoppelung ist sie auf ein DR-Kreuz und auf 8 Flächen des Oktaeders zu beziehen.
4. Die Einzelziffern der ZS+FS 367 sind auf drei verschiedene Figuren anwendbar:
·
Das Hexagon enthält 3
sanduhrförmige Doppeldreiecke aus je 13
Elementen: aus 6 Linien und 5 Punkten + 2
Flächen:
|
|
· Der
Tetraktysrahmen besteht aus 3*6 = 18
Elementen. Zählt man jede Seite allein, sind es 3*7
Elemente:
|
|
· Das
Hexagramm enthält 3 DR. Jede besteht aus 6
Binnenelementen und 7 Punkten.
Erstellt: April 2018