Gematrie und
Vernetzung römischer Dichtung (4)
Beispiel LIBERA
C. Nachweis aus den
Fasti: 8 weitere Verse
III. ZS+FS der
8+8 Verszeilen
a) 8 Verse der FASTI
c) 16 ZW im Achsenkreuz und Oktagon
IV. Weitere Aspekte der 8+8 Verszeilen
Nachdem im vorigen Kapitel die Zahlenwerte (ZW)
der Wortformen LIBERA und LIBERAT in den 8 Versen der Metamorphosen und 8 Versen der Fasti die Absicht Ovids erkennen ließen,
beide Werke als zusammengehörig zu gestalten, sollen nun die ZW der Verszeilen untersucht werden.
a) 8 Verse der FASTI
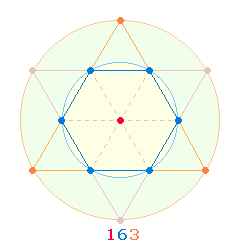
1. Die Zahlensumme (ZS) der 8 Verse beträgt 3019, die Faktorensumme (FS) 326. Die Primzahl 3019 läßt in den Einzelziffern die
Verteilung der 13
Punkte des Tetraktyssterns erkennen: 3 Eckpunkte der 2. Tetraktys, 1 Mittelpunkt + 9 Rahmenpunkte der 1. Tetraktys. In zweistelliger Addition ergeben die
Zahlen 30+19 die 49
Elemente des Tetraktyssterns.
Die FS 326 gibt durch 2*163 die Punkteverteilung der beiden
Tetryktys wieder: 1
Mittelpunkt, 6
hexagonale Kreislinienpunkte und 3
Eckpunkte:
|
|
2.
Die
Verrechnung der ZS+FS führt zu
folgendem Ergebnis:
|
|
ZS |
FS |
Sm |
FW |
Fkt. |
|
|
3019 |
326 |
3345 |
231 |
|
|
FW |
3019 |
165 |
3184 |
207 |
|
|
Sm |
|
|
|
438 |
6*73 |
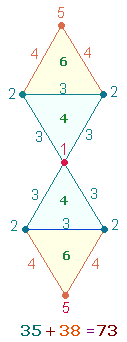
Das Produkt 6*73 ergibt den FW 78, dessen Produkt 3*26 wieder zur FS 326 zurückführt. Die Einzelziffern
der Zahl 78 bezeichnen die 7 Punkte +
8 Linien des Doppelrautenrahmens. Zwei
Doppelrauten (DR) lassen sich zu einem Oktaeder zusammenfügen,
der aus 26 Elementen besteht: 6 Ecken, 8
Flächen, 12 Kanten. Da der Tetraktysstern 3 DR enthält, verbindet sich jede DR
jeweils zweimal mit den anderen und es ergeben sich so aus 6 DR 3 Oktaeder mit insgesamt 3*26 = 78 Elementen.
Ein Numerierungsmodell der DR
ergibt die Summe 73:
|
|
Die Zahl 78 spielt im folgenden Abschnitt
eine wesentliche Rolle.
1. Durch die ZS+FS der 16 Verse muß sich erweisen, ob Ovid
sie als eine Einheit konzipierte:
|
|
Met. |
Fasti |
Sm. |
Fkt. |
|
ZS |
3065 |
3019 |
6084 |
78*78 |
|
FS |
610 |
326 |
936 |
12*78 |
|
Sm. |
|
|
7020 |
|
|
ZS:FS = 78*(12:78) |
||||
Die Quadratzahl von 78 ist als zweifacher DR-Rahmen
anzusehen, die Zahl 12 den Monaten des Jahres
gleichzusetzen, die, wie schon gezeigt wurde, in der Aufteilung 2*6 die Füllelemente der beiden
Rahmen darstellen:
|
|
2. Das interne FS:ZS Verhältnis
beträgt – in weiterer Kürzung – 6*6*13*(2:13). Dieses Verhältnis bezieht sich
am ehesten auf die 3
Achsen des Hexagon mit je 3 Punkten
und 2
Radiallinien.
Wenn man den Mittelpunkt der drei Achsen nur einmal zählt, sind 2 Achsenmittelpunkte abzuziehen.
Die Zahl 13
setzt sich dann aus 7 Punkten
und 6 Linien zusammen.
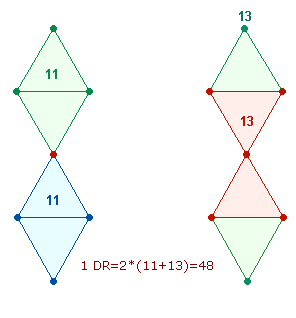
3. Die ZS+FS beträgt 7020 = 540*13 = FW 18+13 = 31. Modell für die Umkehrung der Zahl 13 zur Zahl 31 stehen hauptsächlich die Elemente
der drei Achsen des Hexagon und der Dreiecksseiten der Tetraktys. Auf jede DR
entfällt die Hälfte der ZS+FS = 3*6*13*(2+13) = 234*15 = 3510.
4. Welche Bedeutung hat die homogene
Teilbarkeit durch 13? Die 8+8
Verse entsprechen den Rahmenlinien von 2 Doppelrauten, die man als Achsenkreuz
anordnen kann. Dieses besteht aus 13
Punkten. Statt zusätzlichen 13 Versen wählte Ovid also die Teilbarkeit durch 13, um den Rahmen des DR-Kreuzes zu
vervollständigen.
Um zu sehen, wie Ovid dieses
Modell durchgestaltet hat, sollen die ZW der Verse untersucht werden.
1.
In
der folgenden Tabelle werden die ZW von jeweils 4 Versen der beiden Werke addiert:
|
Vers |
1 |
2 |
3 |
4 |
Sm. |
5 |
6 |
7 |
8 |
Sm. |
GS |
|
M |
408 |
413 |
362 |
361 |
1544 |
417 |
378 |
322 |
404 |
1521 |
3065 |
|
F |
378 |
306 |
450 |
341 |
1475 |
381 |
294 |
410 |
459 |
1544 |
3019 |
|
|
|
|
|
|
3019 |
|
|
|
|
3065 |
|
Es zeigt sich, daß
die Summe der jeweils ersten 4 Versen gleich der Summe der Metamorphosen-ZS ist
und die zweite ZW-Hälfte der Summe der Fasti-ZS entspricht. Zwei versetzte
Hälften haben überdies dieselbe ZS 1544 = 8*193 = FW 199. Der FW 199
bezieht sich auf 19
bzw. 19+9
= 28 Elemente der
Tetraktys. Ovid möchte offensichtlich Doppelrauten und Tetraktys parallel
berücksichtigen.
2.
Die
8 Linien eines DR-Rahmens werden gewöhnlich in umlaufender Reihenfolge (von
unten nach oben, von links nach rechts) besetzt. Ovid wollte also die Anordnung
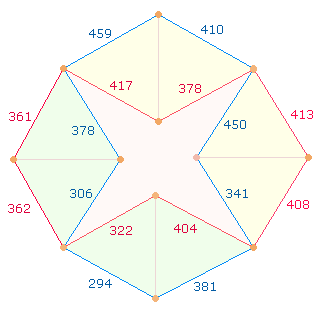
der ZW jeweils mischen. In der folgenden Grafik sind die ZW der Metamorphosen rot, die der Fasti blau bezeichnet:
|
|
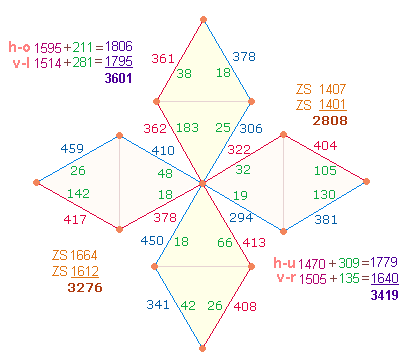
Nachdem die Linien
reihum besetzt wurden, interessieren die Werte der vertikalen und horizontalen Zickzack-Linien. Es entsprechen
sich der linke vertikale und der untere horizontale Linienverlauf sowie die beiden
anderen Linien. Faßt man jeweils die ZS+FS zusammen, sind die Ergebniss 3419 und 3601 durch 13 und die Primzahlfaktoren 263 und 277 teilbar. Die beiden Primzahlen
haben zum Mittelwert 270
den gleichen Abstand. Die Differenz beträgt also 182 = 14*13, das ist auch der ZW von SATOR OPERA TENET des SATOR-Quadrats.
3.
Das
Bestreben der sprachlichen Zahlenkonstrukteure ist es, zwei im rechten Winkel stehende
Rautenwerte zusammenzuschließen. Dies ist hier bei den ZS der unteren und linken Raute
sowie der oberen und rechten der Fall. Das Verhältnis der Ergebnisse 2808:3276 ist 6*6*13 = 468*(6:7). Um dieses Ergebnis zu erreichen,
hat Ovid die 1. und 2. ZS des einen Werkes mit der 3. und 4. des anderen abgestimmt:
|
Vers |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
M |
408 |
413 |
362 |
361 |
417 |
378 |
322 |
404 |
|
F |
378 |
306 |
450 |
341 |
381 |
294 |
410 |
459 |
Nun können die 2 unteren Rauten
(nach rechts oben) zu einem oktogonalen Quadrat verschoben werden:
|
|
Die Außen- und Innenwerte bilden eng beieinander liegende
Verhältnisse:
|
Rauten |
auß. |
inn. |
|
|
o+r |
1690 |
1586 |
2*13*(65:61) |
|
l+u |
1398 |
1410 |
6*(233:235 |
4.
Ovid
unterteilte jeweils 8
Zeilenwerte in zwei Hälften und verband je 2*4 ZW aus beiden Werken so, daß sich die Summen der jeweils 8 getrennten Werte wiederholten (3065, 3019). Bewundernswert ist, daß er auch
das Verhältnis der Faktorenwerte berücksichtigte:
|
Vers |
1 |
2 |
3 |
4 |
Sm. |
5 |
6 |
7 |
8 |
Sm. |
|
M |
26 |
66 |
183 |
38 |
313 |
142 |
18 |
32 |
105 |
297 |
|
F |
18 |
25 |
18 |
42 |
103 |
130 |
19 |
48 |
26 |
223 |
|
|
|
|
|
|
416 |
|
|
|
|
520 |
|
416:520 = 8*13*(4:5) |
||||||||||
5.
Als
Verhältniszahlen der ZS und
FS sind 6:7 und 4:5 ermittelt worden. In diesem
Zusammentreffen dürften sie sich auf zwei Achsenfiguren aus 3 und 2 Achsen beziehen. Die geraden
Zahlen 6 und 4 bezeichnen die Linien, die ungeraden 5 und 7 die Punkte:
|
|
Die DR entsteht zunächst aus dem 3-achsigen Hexagon und
verbindet sich mit einer zweite DR zu einem Achsenkreuz, aus dem ein Oktaeder
gebildet werden kann.
Die Summe der gemeinsamen Teiler
der beiden Verhältnisse ist 468+104 = 572 = 4*13*(9+2) = 4*(13*11). Die Produktzahlen beziehen sich
auf die bereits erwähnten Figuren der Raute und des sanduhrförmigen
Doppeldreiecks, die in einem Oktaeder je 4-mal erkennbar sind, je nachdem, wo
man den Beginn der doppelten Dreiecksfigur setzt:
|
|
Bemerkenswert sind 22+26 als ZS
der
Initialen IN-RI und der Buchstabenzahlen der historischen und der biblischen Kreuzesinschrift.
Erstellt: Mai 2007