Zahlensumme 303 des SATOR-Quadrats in 2
Versen Ovids
I. Einleitung
I. Einleitung
II. Aufteilung der ZS in 112 und 191
III. Viermal 112
VI. Volumenziffern des Oktaeders
1.
Durch mehrere Zufälle fand ich zwei Verse Ovids, die
mehrere gleiche Konstruktionselemente aufweisen. Den ersten habe ich bereits behandelt, zusammen mit dem
zweiten Vers sollen die einzigartigen Gemeinsamkeiten gedeutet werden.
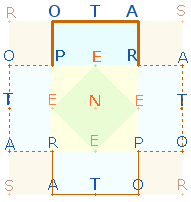
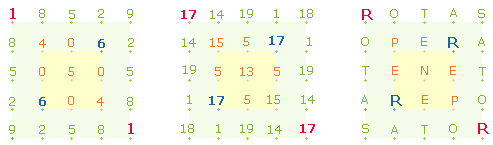
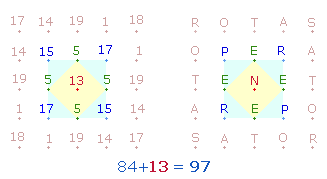
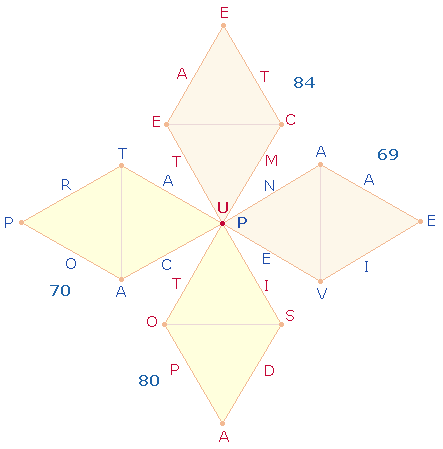
Ausgangspunkt ist die gematrische Dreiteilung der drei Mittelzeilen in je 5
Buchstaben und die Zahlensummen (ZS) 66+33+66:

Aus den äußeren Buchstaben kann man durch Buchstabenumstellung viermal das Wort PORTA bilden:
|
|
|
In den FASTI, einem dichterisch gestalteten römischen Festkalender, bringt Ovid den Marstempel in Beziehung zur PORTA CAPENA. Das Distichon 6, 191-192 lautet:
Lux eadem Marti festa
est, quem prospicit extra
ADPOSITUM TECTAE PORTA CAPENA VIAE:
Derselbe Tag ist auch
dem Mars geweiht, auf (dessen Tempel),
der neben der befestigten Straße gelegen ist, das Capenische Tor schaut.
Der Vers hat dieselbe ZS 303 wie das SATOR-Quadrat.
Ebenfalls durch Buchstabenumstellung wird aus OPERA PAREO – Ich gehorche. In den Metamorphosen Ovids beginnt ein Vers mit PARUIT – er gehorchte, die ZS des Verses ist ebenfalls 303: Aeneas kommt zur Sybille von Cumae, die ihm die Bedingung nennt, um in die Unterwelt zu gelangen. Danach heißt es in Vers 14, 115:
PARUIT AENEAS ET
FORMIDABILIS ORCI
vidit opes ...
Es gehorchte Äneas und des furchtbaren Orkus
Schätze
sah er ...
2.
Die
Metamorphosen wurden 8 n.Chr. veröffentlicht, 6 Bücher der Fasten einige Jahre später. Der Vers aus den Metamorphosen ist als
der frühere anzusehen. Die eingeführte Reihenfolge ist also umzustellen. Die beiden Verse und
ihre Zahlenwerte sind:
PARUIT
AENEAS ET FORMIDABILIS ORCI
|
a(4) e(3) i(5) o(2) u(1) |
V 15 |
112 |
76 |
-36 |
|
b(1) c(1) d(1) f(1) l(1) m(1) n(1) p(1) r(3) s(2) t(2) |
K 15 |
191 |
158 |
-33 |
|
|
30 |
303 |
234 |
-69 |
ADPOSITUM TECTAE PORTA CAPENA VIAE:
|
a(6) e(4) i(2) o(2) u(2) |
V 16 |
112 |
74 |
-38 |
|
c(2) d(1) m(1) n(1) p(3) r(1) s(1) t(4) |
K 14 |
191 |
155 |
-36 |
|
|
30 |
303 |
229 |
-74 |
Auf der Grundlage der gleichen ZS 303 enthalten beide Verse drei Gemeinsamkeiten, die sie über jeden Zufall hinausheben:
·
Die ZS der Vokale
und Konsonanten sind jeweils 112 und 191.
·
Die Wörter FORMIDABILIS
und ADPOSITUM haben jeweils die ZS 112 und die übrigen jeweils vier Wörter die ZS 191.
·
Beide Verse bestehen aus jeweils 5 Wörtern und 30
Buchstaben.
II.
Aufteilung der ZS in 112 und 191
1.
Eine Vertiefung in diese Gemeinsamkeiten führt zu der Erkenntnis,
daß Ovid tiefste Grundlagen des Dezimalsystems und des darauf beruhenden SATOR-Quadrats gestaltete.
Die Zusammenhänge erheben hohen geistigen Anspruch.
Zunächst stellt sich die Frage, wie die beiden ZS im SATOR-Quadrat aufgeteilt sind. 112 besteht sehr wahrscheinlich aus folgenden zwei Buchstabenfolgen:
|
|
OPERA (52), als Imperativ aufgefaßt und verbunden mit PERENE (60) bedeutet Wirke unaufhörlich. Aus den übrigen Zeilen und Buchstaben läßt sich der Satz bilden SATOR (69) ROTAS (69) TOTA (53) – Schöpfer, du drehst alles.
2.
Die beiden ZS haben nur Relevanz, wenn sie in gegenseitiger Verrechnung zu einem sinnvollen
Ergebnis führen:
|
|
|
|
sm |
FW |
|
ZS |
112 |
191 |
303 |
104 |
|
FW |
15 |
191 |
206 |
105 |
|
sm |
|
|
509 |
209 |
|
209 = 11*19 |
||||
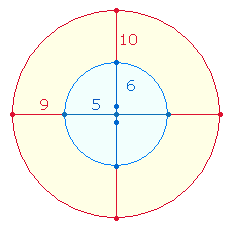
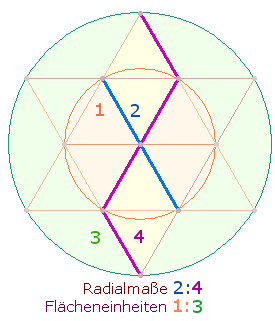
104+105 sind Konstitutivzahlen für ihre Summe 209. 11 und 19 setzen sich aus den Durchmesserelementen und Radialelementen 5+6 und 9+10 der hexagonalen Achse und der DR-Zickzacklinie des Tetraktyssterns zusammen und geben das Kreisflächenverhältnis 1:3 der beiden konzentrischen Kreise wieder:
|
|
206 ist die ZS des äußeren SQ-Rahmens. 303:206 bedeuten 16:12 Flächeneinheiten eines 5x5-Punkte Quadrats, das dem SQ zugrunde liegt. Auf die konzentrischen Kreise des Tetraktyssterns bezogen, beträgt das Kreisflächenverhältnis 3:2.
Den Einzelziffern der Primzahl 509 entsprechen 5:9 Durchmesserelemente der beiden Tetraktyskreise in der Bedeutung von 1:3 Flächeneinheiten.
3.
112 ist aufteilbar in die
Faktoren 16*7.
Die Einzelziffern sind auf die 1+6
Punkte des Hexagons und 7 = 6+1 Punkte des äußeren
Tetraktyskreises zu beziehen. Daraus ergibt sich das Kreisflächenverhältnis 1:(1+2).
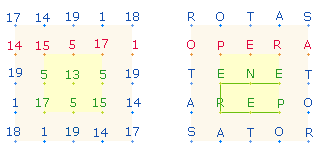
Die FS der ZS 191 im SQ beträgt 156 = 12*13, die ZS+FS 347. In der Aufteilung von 34+7 und in den Einzelziffern 1 6 7 zeigt sich eines der großen Geheimnisse des SQ. Die Vorlage für das SATOR-Quadrat ist das innere 5x5-Quadrat der 1x1 Tabelle ohne Zehnerziffern:
|
|
Im 5x5-Quadrat fehlen die Zahlen 3 und 7, mit der 0 befinden sich also 8 Ziffern im Quadrat. In den Zuordnungen der Ziffern zu den Buchstaben des SQ gibt es zwei Ausnahmen: die Ziffer 5 wird viermal dem T und einmal dem N zugewiesen, hingegen erhalten die Ziffern 1 und 6 jeweils die Zahl 17:
|
|
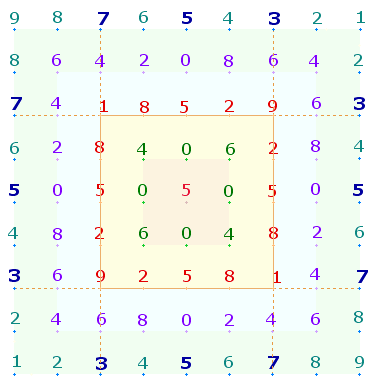
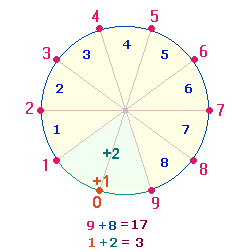
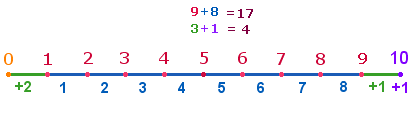
Das Prinzip der 6+1 und 17+17 ist etwa so zu erklären: Die zählbaren Grundzahlen reichen von 1-9. Als Punkte aufgefaßt begrenzen sie 8 Maßeinheiten. Die 1. Maßeinheit beginnt jedoch ab dem Punkt 0. In der Kreisdarstellung fällt der Begrenzungspunkt für die 10. Maßeinheit mit Punkt 0 zusammen:
|
|
|
Auf diese Weise erhält man zusammengefaßt 17+3 Elemente. Soll jedoch die Folge von Maßeinheiten linear weiterlaufen, ist ein 11. Punkt erforderlich. Man kann so zweimal 2+1 Elemente zu 6 zusammenfassen und 1 als 11. Streckenpunkt hinzufügen. Der lineare Verlauf ist daher geprägt vom Punktemuster 1-9-1 und dem Linienmuster 1-8-1. Dieses ist in dreistelliger Zusammensetzung die Summe der 17 Primzahlbuchstaben des SQ: 4*(T+R+A+E) + N = 4*(19+17+1+5) +13 = 168+13 = 181.
Dem Wort SATOR entsprechen in obiger 5x5-Tabelle die Zahlen 92 5 81. Läßt man die Zahl 5 außer Acht, ergibt sich zweistellig 92+81 = 173. Dieselbe Folge von Zahlen zeigt sich auch in den schleifenförmig numerierten Punkten der DR:
|
|
Die vier Zahlen sind kreisförmig gegen den Uhrzeiger zu lesen. Die mittlere Ziffer 5 der 5x5-Tabelle wird durch die zweistellig zusammengesetzte Zahl 19 = T ersetzt, und übernimmt die Stelle der 0 ein.
Der Faktorenwert (FW) von 6 ist 5. So ergibt sich für die zweite Zeile die ZS+FS (6+17)+(5+17) = 23+22 = 45 und für die erste Zeile 2*(17+1) = 36. Die Summe 81 ist die ZS des Wortes PARUIT des M-Verses. Die ZS ist folgendermaßen aufteilbar:
|
|
P |
A |
U |
I |
sm |
R |
T |
sm |
GS |
|
ZW |
15 |
1 |
20 |
9 |
45 |
17 |
19 |
36 |
81 |
1.
Die Zahlen 3 und 4 sind Kreisflächeneinheiten der beiden konzentrischen Kreise des
Tetraktyssterns. Die Summen der Zahlen von 1-3 und 1-4 sind 6+10 = 16. Aus 16+7 ergibt sich dreistellig 167. Zu 167
gelangt man dreistellig durch die ersten drei Zahlen 123 = 3*41 = FW 44; 123+44 = 167. 123 ist im SQ durch die ZS+FS 69+54 von SATOR vertreten, deren FW
26+11 = 37 führen zur 4Wertesumme 160.
Die Konstitutivzahlen 84+83 von 167 haben die FW 14+83 = 97, die ZS des inneren SQ:
|
|
Zwei P ergeben eine Differenz von 14 zwischen FS und ZS, sodaß die FS des inneren Quadrats die Primzahl 83 und eine Konstitutive von 167 ist. 97+84 ergibt erneut die Primzahl 181 und das Muster 1-8-1 der 10 Maßeinheiten.
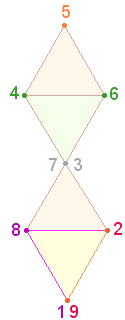
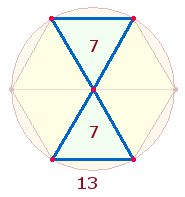
Die drei Einzelziffern bilden durch 1+6 = 7 eine Gleichung. Zweimal 7 ist auf die Elemente von zwei Dreiecken beziehbar. Der FW von 6 ist 5 und so kann aus zwei Dreiecken ein verbundenes Doppeldreieck mit einem gemeinsamen Scheitelpunkt werden:
|
|
Der Doppelaspekt von 14+13 ist ein wesentliches Konstruktionselement des SQ, da je drei Zeilen der Aussage SATOR OPERA TENET die ZS 182 = 14*13 hat und ebenso die ZS+FS der 8 verschiedenen Buchstaben PENSATOR 102+80 = 182 beträgt.
Der Tetraktysstern besteht aus 7+6 Punkten. Nun kann aus der Sicht von zwei Dreiecken vermutet werden, daß ein Punkt fehlt, daß also die hexagonale Erweiterung durch einen zweiten Kreisbogen vollendet wird. Dafür bedarf es jedoch einer zweiten Verwendung des hexagonalen Mittelpunktes, so daß das entscheidende trinitarische Kreisflächenverhältnis 1:3 entsteht.
III. Viermal 112
1.
112 betrifft zweimal die ZS der Vokale und zweimal die Wörter FORMIDABILIS ADPOSITUM. Von Interesse sind die FS:
|
|
ZS |
FS |
sm |
ZS |
FS |
GS |
|
FORMIDABILIS |
112 |
82 |
M-Vok |
112 |
74 |
156 |
|
ADPOSITUM |
112 |
71 |
F-Vok |
112 |
76 |
147 |
|
|
224 |
153 |
|
224 |
150 |
303 |
|
156:147 = 3*(49:52) |
||||||
2.
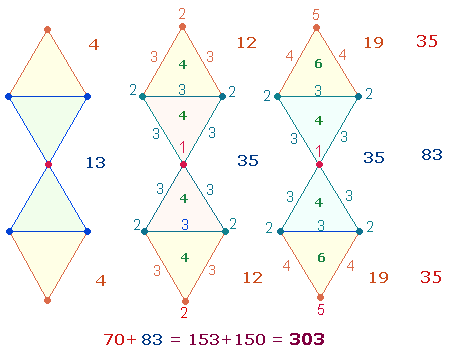
Das FS-Ergebnis 153+150 ist ein
gematrischer Nachweis von 1 unnumeriertem und 2 numerierten DR-Kreuzen, aus denen
jeweils ein Oktaeder zusammengefügt werden kann:
|
|
Die jeweils zweite DR wird ohne Mittelpunkt gezählt. Die drei DR-Kreuze haben die Werte 21+20 = 41; 59+58 = 117 und 73+72 = 145. Letztere Summe ist die Differenz zwischen der FS 303 und der ZS 448.
1. Die Differenz zwischen FS und ZS ist im M-Vers 74 und im F-Vers 69. Die Aufteilung der Vokale und Konsonanten zeigt, daß die beiden
Differenzen komplementär angelegt sind:
|
|
|
|
ZS |
FS
|
sm |
|
M-Vers |
i(5) o(2) u(1) |
V 8 |
93 |
57 |
-36 |
|
|
f(1) m(1) p(1) s(2) |
K 5 |
69 |
36 |
-33 |
|
|
|
13 |
162 |
93 |
-69 |
|
F-Vers |
i(2) o(2) u(2) |
V 6 |
86 |
48 |
-38 |
|
|
m(1) p(3 s(1) |
K 5 |
75 |
39 |
-36 |
|
|
|
11 |
161 |
87 |
-74 |
|
GS |
|
24 |
323 |
180 |
143 |
|
143 = 11*13; 93:87 = 3*(31:29) |
|||||
Beide Verse werden miteinander verbunden, indem die Differenz der Vokale 74 und die der Konsonanten 69 beträgt. Dies ist möglich, da 36 Summe in beiden Versen ist. Die Differenzen stellen die beiden wichtigsten Ordnungsbeziehunen davon Zahlenbeziehungen dar: 36+38 sind die Konstitutivzahlen von 74 und 36+33 bilden das Verhältnis 3*(12:11). Auch die ZS 161+162 sind Konstitutivzahlen.
Den konstitutiven ZS 161+162 von 24 zusammengesetzten ZW entsprechen 36 Primzahlbuchstaben mit den ebenfalls konstitutiven Summen 142+141. Die FW dieser vier Summen sind 30+14 = 44 und 73+50 = 123 und ergeben so zusammen die Systemzahl 167, wie oben ausgeführt.
Die Aufteilung von zusammengesetzten ZW und Primzahlbuchstaben der beiden Verse orientiert sich an den 4 Primzahlen der zweiten Zehnerreihe: 11+19 = 30 und 13+17 = 30.
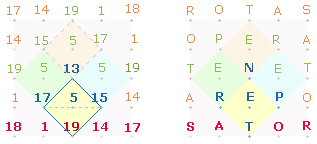
2. 74 und 69 sind
ZS des SATOR-Quadrats:
|
|
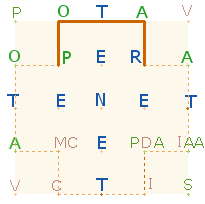
Im großen Rautenquadrat befinden sich 4 kleine Rautenquadrate mit je 5 Buchstaben und der gleichen ZS 69 wie die Wörter SATOR/ROTAS im äußeren Quadratrahmen. Die 5 Buchstaben erhalten nur Sinn, wenn man das E des Mittelpunktes zweimal zu dem Wort PERNET liest. Indem man die 5 Buchstaben des kleinen Rautenquadrats mit SATOR vertauscht, ergibt sich die Aussage SATOR PERNET – Der Schöpfer webt unablässig. SATOR PERNET läßt sich in PATER NOSTER – unser Vater umwandeln.
Im Fasti-Vers macht Ovid die Bedeutung der Differenz 74 deutlich. Er betont sowohl den Doppelaspekt von 5 und 6 Buchstaben des kleinen Rautenquadrats als auch die Austauschbarkeit der 5 Buchstaben mit SATOR. Sinnvoll sind die Faktoren 17*19 der ZS 323, da sie den Buchstaben R und T entsprechen, die sowohl in SATOR als auch in PERNET enthalten sind. Außerdem sind sie die Anzahl der primen ZW des M-V und F-V. Das Verhältnis von primen und zusammengesetzten ZW ist also 36:24 = 13*(3:2); das Verhältnis der SQ-Buchstaben zu den übrigen Buchstaben beträgt 40:20 = 20*(2:1).
1. 30 Buchstaben im Hinblick auf das SATOR-Quadrat kann zwei Bedeutungen haben:
·
Das SATOR-Quadrat
selbst besteht aus zwei Hälften, da die mittlere Zeile zweimal zu lesen ist.
SATOR OPERA
TENET
TENET OPERA
ROTAS
Der Schöpfer erhält
seine Werke;
er hält durch seine
Mühe die Räder.
· In
komplementärer Hinsicht bedeuten 16+15 = 31
Vokale und 14+15 = 29 Konsonanten
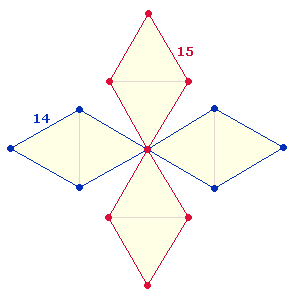
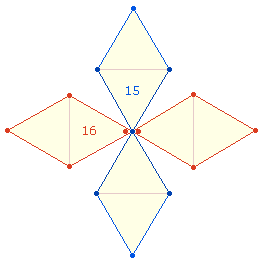
komplementäre Rahmenelememente zweier DR-Kreuze:
|
|
|
Ovid könnte auf zwei Gesichtspunkte geachtet haben: Erstens auf die Anordnung von 30 Buchstaben auf den 25 Punkten des SATOR-Quadrats, zweitens auf ihre Anordnung auf zweimal 15 Rahmenelemente.
Die Zahlen 31 und 29 wurden bereits oben als Verhältniszahlen der FS 93 und 87 der 13+11 zusammengesetzten ZW ermittelt.
Die ZS der horizontalen und vertikalen Zeilen der beiden folgenden Buchstabenquadrate aus dem Metamorphosen- und dem Fasti-Vers entsprechen denen des SQ:
|
|
|
Die blauen und grünen Buchstaben sind SQ-Buchstaben, in Fettdruck in gleicher Position wie im SQ. Die Verteilung der in gleicher und verschiedener Position angeordneten SQ-Bu. ist 16+2 = 18 und 16+6 = 22. Es könnten mehrere Anordnungen möglich sein, die hier erstellten erbringen erstaunlicherweise dieselbe ZS+FS 327 für die an originaler Position stehenden Buchstaben:
|
M-V |
|
A |
E |
N |
R |
T |
sm |
O |
P |
S |
sm |
GS |
Rest |
|
|
Hfk. |
3 |
3 |
1 |
2 |
2 |
11 |
2 |
1 |
2 |
5 |
16 |
14 |
|
|
ZS |
3 |
15 |
13 |
34 |
38 |
103 |
28 |
15 |
36 |
79 |
182 |
121 |
|
|
FS |
|
|
|
|
|
103 |
18 |
8 |
16 |
42 |
145 |
89 |
|
|
|
|
|
|
|
|
206 |
|
|
|
121 |
327 |
210 |
|
F-V |
|
A |
E |
N |
R |
T |
sm |
O |
P |
S |
sm |
GS |
Rest |
|
|
Hfk. |
3 |
4 |
1 |
1 |
4 |
13 |
2 |
1 |
– |
3 |
16 |
14 |
|
|
ZS |
3 |
20 |
13 |
17 |
76 |
129 |
28 |
15 |
– |
43 |
172 |
131 |
|
|
FS |
|
|
|
|
|
129 |
18 |
8 |
– |
26 |
155 |
74 |
|
|
|
|
|
|
|
|
258 |
|
|
|
69 |
327 |
205 |
|
210:205 = 5*(42:41) = 5*83 = 415 |
|||||||||||||
Die Zahl der zusammengesetzten ZW entspricht der des SQ, und damit auch die Differenzsumme 54, aufgeteilt in 37+17.
Der FW von 327 = 3*109 ist wiederum die thematische Zahl 112. 109 steht für die ZS des TENET-Kreuzes, die Einzelziffern von 3*109 geben die 13 Punkte des Tetraktyssterns wieder.
Für alle SQ-Buchstaben ergibt sich:
|
|
|
PZ |
|
zg. Z |
|
|
Diff. |
||
|
M-V |
|
ZS |
ZS |
sm |
ZS |
ZS |
sm |
GS |
|
|
|
Hfk. |
11 |
2 |
13 |
5 |
– |
5 |
18 |
|
|
|
ZS |
103 |
18 |
121 |
79 |
– |
79 |
200 |
|
|
|
FS |
103 |
18 |
121 |
42 |
– |
42 |
163 |
-37 |
|
|
|
|
|
242 |
121 |
– |
121 |
363 |
>25 |
|
|
|
PZ |
|
zg. Z |
|
|
Diff. |
||
|
F-V |
|
ZS |
ZS |
sm |
ZS |
ZS |
sm |
GS |
|
|
|
Hfk. |
13 |
3 |
16 |
3 |
3 |
6 |
22 |
|
|
|
ZS |
129 |
3 |
132 |
43 |
48 |
91 |
223 |
|
|
|
FS |
129 |
3 |
132 |
26 |
24 |
50 |
182 |
-41 |
|
|
|
|
|
264 |
69 |
72 |
141 |
405 |
>17 |
Das FS:ZS-Verhältnis beträgt (163+182):(200+223) = 345:423 = 3*(115:141) = 3*256 = 768 = 12*64. Die Faktorenwerte sind 345 = 15*23 >31, 423 = 9*47 >53; 31+53 = 84. Die Einzelziffern der FW stellen das Kreisflächenverhältnis 3:1 in Entsprechung zu 5:3 Radialelementen der DR-Zickzacklinie dar:
|
|
Die Zahlen 64 und 84 sind auf den inneren Quadratrahmen des SQ beziehbar, dessen Eckbuchstaben RP jeweils die ZS 32 haben und durch 4 E 84 ergeben, die FW 17 und 25 auf Numerierungssummen einer Tetraktysseite.
Die
Differenzwerte 37+41 = 78 sind die mittleren
von 26 Primzahlen von 1-100, sie stellen die Elemente der Tetraktys und der
DR-Kreuzes dar. Die Differenzen aus den übrigen
zusammengesetzten Buchstaben-ZW sind 37+28 = 65,
das Verhältnis der Summen 78:65 beträgt 13*(6:5). Die beiden Summen sind FW1/2-Ergebnisse der Wörter SATOR PERNET. Die 4W-Summen
sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
SATOR |
69 |
54 |
123 |
26 |
11 |
37 |
160 |
|
PERNET |
74 |
67 |
141 |
39 |
67 |
106 |
247 |
|
|
143 |
121 |
264 |
65 |
78 |
143 |
407 |
|
(143:121):143 = 11*(13:11:13) = 11*(24:13) |
|||||||
Die Einzelziffern des Verhältnisses 24:13 geben die
Entsprechung von Maßeinheiten und Kreisflächeneinheiten
wieder:
|
|
Die ZS+FS der übrigen 20
Buchstaben beträgt 183+118
= 301 = 7*43. Die ZW/FW-Verrechnung
führt zur systemrelevanten Zahl 167 (s.o.):
|
|
ZS+FS |
sm |
FW |
sm |
FW |
|
|
|
768 |
301 |
1069 |
1069 |
|
|
|
FW |
19 |
50 |
69 |
26 |
|
|
|
sm |
|
|
1138 |
1095 |
|
|
|
FW |
|
|
571 |
81 |
652 |
167 |
|
sm |
652 = 4*163 |
|||||
Den FW 19+50 entsprechen die Buchstaben SA+TOR.
Die Aufteilung in übrigen primen und zusammengesetzten ZW führt zu folgendem Ergebnis:
|
|
|
B |
C |
D |
L |
sm |
I |
V |
F |
M |
sm |
GS |
|
M-V |
Hfk. |
1 |
1 |
1 |
1 |
4 |
5 |
1 |
1 |
1 |
8 |
12 |
|
F-V |
Hfk. |
- |
2 |
1 |
- |
3 |
2 |
2 |
- |
1 |
5 |
8 |
|
sm |
|
1 |
2 |
1 |
1 |
7 |
7 |
3 |
1 |
2 |
13 |
20 |
|
M-V |
ZS |
2 |
3 |
4 |
11 |
20 |
45 |
20 |
6 |
12 |
83 |
103 |
|
F-V |
ZS |
- |
6 |
4 |
- |
10 |
18 |
40 |
- |
12 |
70 |
80 |
|
sm |
|
|
|
|
|
30 |
|
|
|
|
153 |
183 |
|
FS |
|
|
|
|
|
20 |
30 |
9 |
5 |
7 |
51 |
71 |
|
FS |
|
|
|
|
|
10 |
12 |
18 |
- |
7 |
37 |
47 |
|
sm |
|
|
|
|
|
30 |
42 |
27 |
5 |
|
88 |
118 |
|
GS |
|
|
|
|
|
|
|
|
|
|
|
301 |
|
103+71
= 174; 80+47 = 127 |
||||||||||||
2. Die Buchstaben jedes Verses werden von unten nach
oben und von links nach rechts im linearen und Zickzackverlauf auf den
Rahmenelementen der beiden DR-Kreuze angeordnet:
|
|
|
Die ZS der jeweils unteren und linken Raute beträgt 150, die der oberen und rechten 153. Die entsprechenden Buchstabenzahlen sind 29 und 31; Die Zugehörigkeit der Mittelpunktbuchstaben ist nicht festgelegt, sie können jeweils einer von zwei Rauten zugeteilt werden. Die ZS der unteren und oberen Pyramide betragen 191+241 = 432, die ZS der gemeinsamen Mittelbasis von 16 Querlinienpunkten 174.
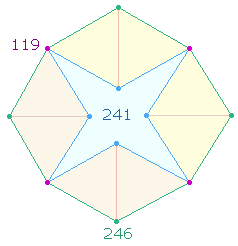
Durch Winkelverschiebung erhält man ein Oktogon:
|
|
24 innere und 24 äußere "Dachelemente" haben die ZS 241 und 246, das Verhältnis der 4 inneren zu den 8 äußeren Punkte-ZW beträgt 49:70 = 7*(7:10) = 119. Zweimalige ZS 241 ist auf 24+1 Elemente des Hexagons und des äußeren Tetraktyskreises mit eigenem Mittelpunkt zu beziehen.
Erstellt: April 2020