Entfaltung des Dezimalsystems aus seinem
ontologischen Ursprung
Der trinitarische Aspekt, der in diesem Artikel eine wichtige
Rolle spielt, kann zwar weitgehend ausgeblendet werden, sollte aber dennoch mitgedacht
werden. Denn nur so ist der Glaube an ein Sinngefüge der Zahlen möglich. Im
Folgenden geht es um Achsenkreuze aus drei Achsen, die dem Hexagon zugrunde
liegen. Achsenkreuze aus zwei Achsen sind an
anderer Stelle behandelt.
Ähnliche Entwicklungslinien des Dezimalsystems enthält auch die
Ausarbeitung Die trinitarische Gleichung 1+2=3.
INHALT
I.
Die Strecke
II.
Der Kreis
III.
Kreisdurchmesser
und Kreishälften
IV.
Das Hexagon
VI.
Erweiterung zum Tetraktysstern
VII.
Die Tetraktys
VIII.
Die
Doppelraute (I)
XI.
Der Oktaeder
Wie im Einleitungskapitel "Das ontologische Prinzip";
dargelegt wurde, ist alles Endliche Abbild des Unendlichen. Jedes Seiende kann
als Zeichen verstanden werden, das sowohl Selbstsein besitzt als auch über sich
selbst hinausweist und damit Zeichencharakter oder Symbolwert besitzt. Ein
Seiendes weist naturgemäß darin über sich hinaus, daß es Element eines Ganzen
ist und als solches Funktion hat.
Gegenstand der Mathematik sind die Ideen des Endlichen. Ideen sind
vollkommene Maßstäbe des Endlichen. Sie sind gewissermaßen Mittler zwischen dem
Ungeschaffenen und dem Geschaffenen. Deshalb besitzen insbesondere Elemente der
Geometrie Zeichencharakter. Diesen zu verstehen, ist die schwierige Aufgabe,
die sich bei der Darstellung des Zahlensystems stellt, eine Aufgabe, die
vielleicht nicht immer oder nur unvollständig gelingt, die aber dennoch gewagt werden muß.
Die Frage nach Entstehung und Wesen der Zahlen kann etwa so
beantwortet werden: Einerseits sind sie immateriellen Ideen vergleichbar, im
Wesen göttlicher Weisheit verankert. Andererseits sind sie allem Geschaffenen –
Zeit, Raum, Materie – untrennbar mitgegeben und stiften dem Geschaffenen Zweck
und Sinn ein, wie er sich aus ihrer jeweiligen Stellung im Sinngefüge aller
Zahlen und ihrer Herkunft aus ihrem trinitarischen Urgrund ergibt.
Zahlen sind nicht einfach Verfügungsmasse menschlicher
Gehirntätigkeit, sondern stellen eine objektive Ordnung dar. Die Entfaltung
ihrer Logik geschieht aus den absoluten und wesensgemäßen Beziehungen der drei
göttlichen Personen zueinander als einer Einheit. Ideelle Ausdrucksformen
dieser Beziehungen sind außer den Zahlen selbst alle geometrischen und
räumlichen Figuren. Von ihrer Gegebenheit läßt sich auf die Gegebenheit der
trinitarischen Personen schließen und umgekehrt. Zwischen beiden Gegebenheiten
herrscht parallele Logik. Die Definition des Kreises etwa ist auch eine der
Definitionen, die für die Trinität gilt.
Erforschung des Dezimalsystems bedeutet, die Entfaltung
der Zahlen als einen Prozeß zu begreifen, dessen Dynamik aus dem Wesen der
innertrinitarischen Beziehungen erwächst. Mit der Entfaltung der Zahlen einher
gehen Prinzipien, die jede nachfolgende Zahl mit allen vorangehenden verbinden.
Der Einwand, die Einführung einer religiösen Kategorie
verstoße gegen das Prinzip rationaler Wissenschaft, könnte durch folgende
Überlegung überwunden werden: Die göttliche Weisheit selbst ist der Inbegriff
der Rationalität. Der Wissenschaft der göttlichen Weisheit sollte der Vorrang
vor jeder anderen Wissenschaft gebühren, da sie allein voraussetzungslos ist.
I. DIE STRECKE
Um den Anfang
der Darstellung des Zahlensystems zu setzen, können wir entweder vom Endlichen
als Gegebenheit ausgehen oder vom Unendlichen, aus dem das Endliche hervorgeht.
Gehen wir vom Endlichen aus, ist die Strecke das Grundelement von Raum und
Zeit. Sie besteht aus zwei Punkten und einer verbindenden Linie. Die beiden
Punkte (P) bezeichnen die Begrenzung des Endlichen. Die verbindende Linie (L)
hat statischen, dynamischen und organischen Charakter. In statischer Hinsicht bedeutet sie meßbare Entfernung, in
dynamischer einen Weg von einem Punkt zum anderen. Daher kann der Ausgangspunkt
als 1, der
Zielpunkt als 2 bezeichnet werden. Organischen Symbolcharakter hat die Linie darin, daß
sie die Summe alles Endlichen als zusammengehörig kennzeichnet.
|
|
Die dargestellte Strecke bildet
gewissermaßen das Urmaß jeder weiteren endlichen Ausdehnung. Als dreistellige
Zahl hat 112 eine vielfältige Bedeutung
für das Dezimalsystem. Es können von 1-9 acht dreistellige Zahlen gebildet
werden.
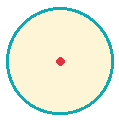
Der Kreis hat wie die Strecke einen Ausgangspunkt, den Mittelpunkt (MP).
Der MP setzt das Maß seiner selbst in einem imaginären Punkt als Beginn der Kreislinie
– imaginär entsprechend der Kreisdefinition: Der Kreis ist der Ort aller
Punkte, die vom MP gleichweit entfernt sind. Der zweite Punkt der Strecke ist
also aufgehoben in der Kreislinie. Die Kreislinie stellt daher nicht eigentlich
eine Begrenzung dar, sondern ist die Idee des Maßes, das benötigt wird, um die
Abbildlichkeit des Mittelpunktes darzustellen. Die Abbildlichkeit ist nicht in
eine bestimmte Richtung hin festgelegt (ohne Punkt), sondern allumfassend.
Entsprechend ist auch die umschlossene Fläche als universal aufzufassen. In
endlicher Hinsicht symbolisiert die Kreisfläche die Gesamtheit des Räumlichen.
Auf der Ebene
des Unendlichen hat der Kreis trinitarischen Charakter. Die erste Person teilt
der zweiten Person die Fülle der Gottheit mit und bringt zusammen mit ihr die
dritte Person hervor, welche im Streckenmaß des Radius ihren Ausgang und in der
Umschließung des Kreises ihre Vollendung findet. Aus der Einzigkeit des
Mittelpunktes entfaltet sich die Dreiheit des Kreises.
|
|
Die Kreislinie
ist richtungslos und hat keinen Anfang und kein Ende. Da sie keinen Endpunkt
hat, reflektiert sie auf ihren Ausgangspunkt zurück. Die unendlich gleiche Rundung
der Kreislinie bezeichnet die vollkommene Selbsterkenntnis und den Selbstbesitz
der ersten göttlichen Person. Ein anderer Begriff dafür ist
Identität.
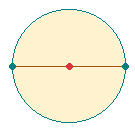
III. KREISDURCHMESSER UND KREISHÄLFTEN
Die Kreislinie ist sowohl als ganze als auch von jeder beliebigen Stelle
auf den MP hingeordnet. In letzterem Fall ist eine Linie zu denken, die von der
Kreislinie zum MP führt und in ihrer Fortsetzung in einem Gegenpol endet. Die
Spiegelbildlichkeit der beiden Punkte bedeutet den vollkommenen Selbstbesitz
der zweiten Person, so daß die Zahl 2 zum Inbegriff der Identität wird. Mit der
zweiten Person ist auch die dritte Person als identisch mit sich selbst durch
zwei Linien, die den Durchmesser (DM) bilden, gegeben.
Selbstbesitz und Identität als Wesensmerkmale der göttlichen Dreifaltigkeit
werden also durch zwei gleiche Hälften des Durchmessers und des Kreises auf der
elementarsten Stufe wiedergegeben. Damit liegen auch die ersten
Zahlenverhältnisse für die Entfaltung des Dezimalsystems fest:
|
|
1. Nach der Dreiheit der Strecke und
des Kreises ist mit den 5 Elementen des DM eine weitere numerische Einheit
gegeben. Nimmt man Punkte und Linien zusammen, ergibt sich das Verhältnis 3:2, faßt man die symmetrischen
Elemente zusammen, ist das Verhältnis 4:1 bzw. 2:2:1 mit ihren entsprechenden Umkehrungen. Im römischen Zahlensystem ist
die 5 die erste
höhere Zahlebene.
2. Nimmt man die beiden Kreishälften
hinzu (2 halbe Kreislinien, 2 halbe Kreisflächen), wachsen die 3
Ausgangselemente des Kreises auf ihre Quadratzahl 9. Das Quadrat aber stellt ebenso
ein Identitätsmuster dar. Das Verhältnis der drei Bereiche stellt sich dar als 2:5:2.
3. Die Zahl 5 bildet das Grundmuster
der Symmetrie: zwei gleiche Einheiten auf jeder Seite mit einem gemeinsamen
Mittelpunkt. Die beiden Linien stellen die "Füllung" zwischen Anfang,
Mitte und Ende dar.
4. Der DM besteht einerseits aus 5
Elementen, andererseits aus 2 Radien mit je einem Mittelpunkt. Daraus ergibt
sich eine doppelte Zählweise von 5+6=11. Die Zahlen der drei
symmetrischen Teile sind demnach 4-3-4. In allen Gedichten achtet z.B. Catull
auf die gematrische Auszählung des ersten, mittleren
bzw. der beiden mittleren und des letzten Buchstabens. Besonders kunstvoll hat Catull dies im 19 Verse umfassenden Carmen 8 erreicht, wo der Umschlag der
Gefühle durch Umkehrung der Zahlenwerte von 203 zu 302 und zurück zu
203 verdeutlicht wird.
5. Auch die beiden Kreishälften
verlangen eine doppelte Zählweise der Elemente. Je eine Hälfte besteht aus 7 Elementen, der Kreis als ganzer
aus 9 Elementen,
zusammen 14+9=23.
Die Idee des Kreises ist nicht nur eine Widerspiegelung der göttlichen
Dreifaltigkeit, sondern auch ein Modell für die bewegte Ordnung der Schöpfung.
Unzählige Vorgänge verlaufen in Kreisbahnen, die Bewegung der Gestirne, der
Kreislauf der Natur, Regelkreise des Organismus und Schaltkreise in der Physik.
Daher sollte es nicht verwundern, daß das Dezimalsystem die Zahlenidee all
dieser Kreisläufe darstellt.
|
|
|
1.
Der Kreisbogen zeigt, wie sich
die 1. Person in der Setzung der 2. Person wiedererkennt und so ihre vollkommene
Identität und ihren Selbstbesitz hat. Indem sich die 1. Person ein Maß setzt,
um die 2. Person zu setzen und indem diese auf die 1. Person hingeordnet ist,
geht durch dialogische Situation die dritte Person hervor. Während also die 2
aus der 1 durch Setzung hervorgeht, ist die Drei die erste Zahl unter allen
übrigen, die aus zwei Zahlen entsteht. Die Drei ist außerdem die einzige Zahl,
die aus den beiden vorhergehenden entsteht. Die 3. Person ist also die
Gemeinsamkeit von 1 und 2. Da die drei göttlichen Personen durch vollkommenen
Selbstbesitz das gleiche Wesen haben und durch Dialogsituation eine vollkommene
Gemeinschaft bilden, erhält diese Gemeinschaft ihre vollkommene Identität durch
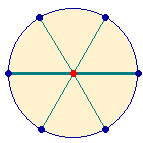
Addition von 1+2+3 = 6. Indem nun das Maß des Radius 6-mal die Kreislinie
schneidet, lassen sich neben dem ersten Durchmesser zwei weitere durch den
Mittelpunkt ziehen und es entstehen 6 abgeteilte Flächen, von denen sich
jeweils zwei spiegelbildlich gegenüberstehen. Die drei spiegelverkehrten
Flächenfiguren bezeichnen das gleiche Wesen der drei göttlichen Personen und vollkommenen Selbstbesitz.
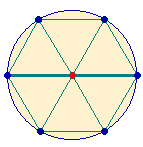
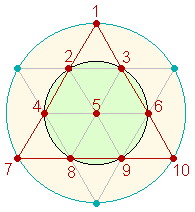
2.
Ein Hexagon besteht aus 25 Elementen: 7 Punkten, 6 Dreiecken und 12 Linien. Der Kreis mit seinen 3 Elementen als Ursprung des Hexagons besitzt jedoch
weiterhin seine Zählfunktion. Wir zählen also 28 Elemente
und stehen damit in Übereinstimmung mit der Summe der (numerierten) Punkte 1-7. Zählt man
den Mittelpunkt nur einmal, sind es 27 Elemente. Die Addition dieses
Doppelaspekts ergibt 55, die Summe der Zahlen 1-10. Auf diese Weise dokumentiert bereits der einfache Kreis
mit dem eingeschriebenen Hexagon das Dezimalsystem.
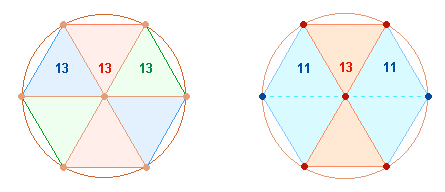
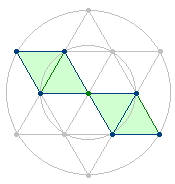
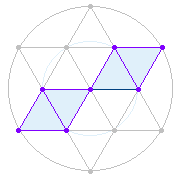
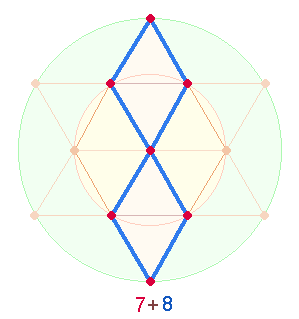
3. Das Hexagon enthält zwei geometrische
Figurenkonstellationen: einmal 3 gleiche Doppeldreiecke, deren Scheitelpunkte
sich im Mittelpunkt kreuzen, und einmal ein linkes und ein rechtes
rautenförmiges Doppeldreieck mit einem sanduhrförmigen Doppeldreieck in der
Mitte:
|
|
Die Doppeldreiecke der linken Grafik bestehen aus 5 Punkten + 2 Flächen und 6 Linien = 13 Elementen, die Rautendreiecke aus 4 Punkten + 2 Flächen und 5 Linien = 11 Elementen.
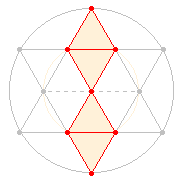
Die Figurenkonstellation der rechten Seite ist von besonderer Bedeutung.
Denn die beiden Rauten mit je 11 Elementen ergeben zusammen
die Zahl 22, deren Faktorenwert (FW) 2*11 = 13 beträgt. Die
Mittelfigur mit ihren 13 Elementen wird somit durch die
beiden Seitenfiguren hervorgebracht. Unter trinitarischem Gesichtpunkt kann
somit die Mittelfigur der 3. Person zugeordnet werden.
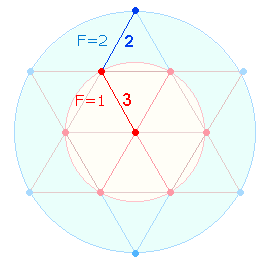
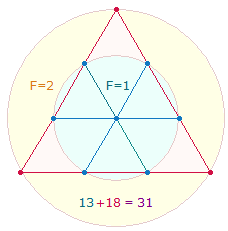
Als
Einzelziffern sind die Zahlen 13 und 22 im Tetraktysstern relevant. Der innere Kreis hat die
Flächengröße 1 und 3 Radialelemente, der äußere Kreisring die Flächengröße 2 und 2
Radialelemente:
|
|
Die trinitarische Situation ist hier jedoch
verschieden.
Man könnte von einem
Rollentausch sprechen: Der innere Kreis steht für die 1. Person, die gleichzeitig Prinzip der Einheit
der sie selbst einschließenden 3 Personen ist. Die Fläche 2 kann für die 2. und 3. Person, die 2 Radialelemente für die 2. Person allein stehen.
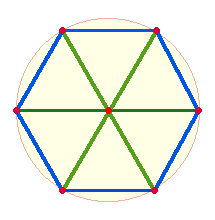
Verbindet man die 6 Kreispunkte durch Linien, entstehen
6 gleichseitige Dreiecke. Die drei gleichen Seiten eines Dreiecks bezeichnen
das gleiche Wesen der drei Personen. Die geringste Zahl von Linien, die eine
Fläche umgrenzen, ist drei. Die Fläche schafft eine neue Dimension. Während der
Kreis die drei Personen in einer dynamisch-dialogischen Form zeigt, zeigt das
Dreieck in konstatierender Weise auf, daß die drei Personen in der Fläche eine
Einheit bilden. Die 4 bezeichnet also die Einheit der Personen. Die
Konstitutiven der 4 sind 3+1. Die beiden Zahlen 13 und 31 geben in besonderer
Weise die Formel der Dreifaltigkeit als ein Gott in drei Personen wieder.
Zählt man neben den drei Seiten auch die drei
Punkte, stellt sich die Einheit der drei Personen als 61 bzw. 16 dar. Dies entspricht auch den 6 Punkten der
Kreislinie und dem MP.
Nach einer weiteren Sichtweise wird jede Seite von
2 Punkten begrenzt. Dies ergibt die Quadratzahl 9, die in neuer Form das
identische Wesen der 3 Personen bestätigt. Die begrenzenden Punkte könnten
Sinnbild der Dreifaltigkeitsformel "Unterschied der Person, Gleichheit des
Wesens" (in personis proprietas, in essentia unitas) sein, indem
die Punkte das Wesen, die Linien die Person darstellen.
Was durch letztere Zählweise als 3³ +1 erscheint, ist in der Addition der ersten vier Zahlen verwirklicht:
(1+2+3) +4 = 10. Ein Zähler aus der 4 gibt somit den ersten 10 Zahlen ihre
Einheit: 9+1= [6+(3]+1).
Die Zahl 10 wird durch die bereits
existierende Zahl 1 und die 0 (Null), d.h. durch das NICHTS dargestellt. Für das
römische Zahlsystem bedeutet das Zahlzeichen X für 10 den Beginn einer höheren Zähleinheit, der sich weitere anschließen, so wie
das Zahlzeichen I den Beginn der Grundzahlen von 1-9 bezeichnet.
Auf die Ebene des Endlichen bezogen ist das Nichts
ein Hinweis auf die Herkunft des Endlichen aus dem Nicht-Endlichen. In der 10
vollendet das Unerschaffene das Erschaffene. Bekanntlich wurde das römische K als 10. Buchstabe (abgesehen von der Abkürzung des Vornamens Kaeso)
nur für Kalendae verwendet. Die Kalenden bezeichneten den ersten Tag
nach dem Neumond, also nachdem der Mond aus dem Nichts zur Sichtbarkeit
zurückkehrt. In der römische Religion gab es offenbar eine besondere
Sensibilität für dieses metaphysisch interpretierbare Nichts.
Schließlich sei noch auf eine Eigenheit von Cäsars Kalenderreform eingegangen. Ursprünglich hatte das römische Jahr
nur 10 Monate, was aus dem Namen Dezember abzulesen ist. Das Jahr begann also
im März. Nun lassen sich im Hexagon drei Achsen durch den MP ziehen, jede mit 5
Elementen in der Abfolge P-L-P-L-P. Diese Struktur ist an der Zahl der Kalendertage
ablesbar, wenn man mit den 31 Tagen des März beginnt. Wenn man die Punkte mit
Monaten von 31 Tagen gleichsetzt, so stoßen nach jeder 5-er Einheit zwei Monate
mit je 31 Tagen zusammen: Juli-August, Dezember-Januar. Auf diese Weise ist das
Jahr auf die konkurrierenden Zahlen 5 u. 6 aufgebaut und neben den expliziten
12 Monaten sind noch implizit die Zahlen 10 (März bis Dezember) und 15 (März
bis Mai des folgenden Jahres) integriert.
VI. Erweiterung zum Tetraktysstern
1. Die drei Hexagon-Achsen bestehen aus je zwei symmetrischen Radiallinien. Werden
die 6
Punkte des Kreisbogens durch Linien (Segmentlinien) verbunden, entstehen 6 Dreiecke. Das
gesamte Hexagon kann so in das Verhältnis 6*(2:1) Radialmaße gefaßt werden:
|
|
Errichtet man über jede Segementlinie mittels
Zirkelschnittpunkte ein Dreieck, erhält man 6 Strecken aus jeweils 3
Radialmaßen:
|
|
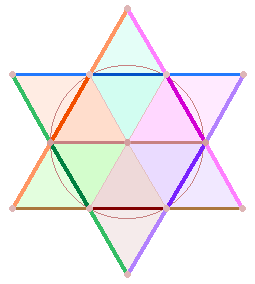
2. Die 3 Hexagonachsen werden nun umschlossen von 2*3 = 6
Dreiecksseiten, die 2 symmetrisch verschränkte Dreiecke bilden. Die 6
Segmentlinien sind nun Zentraleinheiten mit je einem linken und rechten
Seitenflügel.
Ein Segmentlinie bildet ein doppeltes Verhältnis
zu den neu dazugekommenen: 1:2 Radiallinien unter dem Erweiterungsaspekt und 1:3 Radiallinien unter dem getrennten Gesichtspunkt eines
hexagonalen Radialmaßes zu drei Maßen der ganzenTetraktysseite.
VII. DieTetraktys (Dezimaldreieck)
1.
Die Entwicklung des Hexagon zum
Tetraktysstern vollzog sich auf der Grundlage von 1-3 Radialmaßen. Das
Ergebnis beschert nun in der berühmten Anordnung der Punkte 1-4 die berühmte Tetraktys des
Pythagoras und zwar in doppelter ineinander verschränkter Gestalt. Pythagoras
erkannte darin z.B. harmonische Gesetze der Musik. Hier soll es jedoch
ausschließlich um die Bedeutung dieser Figur für die Ordnung des Dezimalsystems
gehen:
|
|
2.
Eine Tetraktys setzt sich zusammen
aus dem Mittelpunkt, 6 hexagonalen Punkten und 3 Eckpunkten. Die entsprechende
dreistellige Zahl 163 ist eine Primzahl, ebenso 613 und 631. Sieht man
den Tetraktysrahmen mit 9 Punkten als eine Einheit, sind die 13 Punkte des Tetraktyssterns aufteilbar in 1+9+3. Im römischen Staat stimmen bei Wahlen der centuria centuriata 193 Körperschaften ab,
die nach Steuerklassen eingeteilt sind. Diese ursprüngliche Einteilung wurde
seit dem Ende des 3.Jh. auf 373 Stimmabteilungen erweitert. Diese Zahl entspricht den 3 Eckpunkten des
ersten Dezimaldreiecks, den 7 Punkten des inneren Kreises und drei Punkten des
zweiten DzDr.
3. Die Tetraktys
kann nach den verschiedensten Gesichtspunkten untersucht werden. Auf die wohl
wichtigste sei hier eingegangen. Jede Seite der Tetraktys besteht aus 4P+3L. Addiert ergeben sich die Zahlen 12+9=21. Die 3 Seiten zeigen hier die
Bedeutung der Umkehrzahlen im 2-stelligen Bereich, die bereits genannt wurde.
Auf drei Seiten manifestieren sich hier die drei göttlichen Personen (3L) in der Einheit (3+1P). Fügt man das Produkt 3*(4+3) zur dreistelligen Zahl 343 zusammen,
erhält man als Teilungsfaktoren 7*7*7. Auch die
Hoheitsformel SENATVS POPVLVSQUE ROMANVS hat den
Zahlenwert 343.
4. Die Tetraktys
besteht aus 37 Elementen: 10 Punkten + 9 Dreiecken + 18 Linien. Punkte und Dreiecke bilden gewöhnlich eine Einheit und kommen auf einen
Zähler mehr als die Linien. Das Produkt der Einzelziffern 3*7 gibt die Zahl der 21 Elemente der
3 Tetraktysseiten wieder.
Der Addition 18+19 entsprechen die Buchstaben ST, die sich
als Schweigegebot in Ciceros Somnium Scipionis finden. Die Bedeutung dieser
Buchstabenverbindung zeigt sich in den Faktorenwerten (FW) der zusammengesetzten 4-stelligen Zahl 1819 = 17*107 = FW 124 = 4*31. Die Zahlen 18+19 und die Faktoren 17*107 scheinen trinitarisch
zusammenzustimmen: Nimmt man 10 als Komplementärzahl zu 1 an, entsprechen die
Konstitutiven 10+9 = 19 und 10+8 = 18 den Verhältnissen 1+2 und 1+3, die in den Ziffern des FW 124
zusammengefaßt sind. Der Faktor 107 teilt die
Zahl 17 auf in 10 Punkte der Tetraktys und 7 Punkte des Hexagon. Die
Tetraktys steht für die Kreisfläche 3 des äußeren
Kreises, das Hexagon für die Kreisfläche 1 des inneren
Kreises, die Zahl 17 faßt das
Verhältnis 3:1 in der Zahl 4 zusammen,
sodaß sich das Produkt 4*31 als trinitarische Gleichung 4=3+1 zeigt.
Von den schon unter dem vorherigen
Abschnitt behandelten Umkehrungen der Zahlen 235 und 347 führen die ZS+FS der gemeinsamen Dreihunderter-Reihe ebenso zur Zahl 1819:
|
ZW |
325 |
352 |
347 |
374 |
1398 |
|
FW |
23 |
21 |
347 |
30 |
421 |
|
Sm. |
|
|
|
|
1819 |
Bemerkenswert ist die Primzahl 421 als Umkehrung des FW 124 von 1819. Man erkennt die
Reihenfolge der Einzelziffern auf der linken numerierten Kathete der Tetraktys und
als Entsprechung die Zahlen 136 auf der rechten Kathete. Die Einzelziffern
ergeben wiederum 7+10 = 17.
5. Indem
jedeTetraktys aus 10 Punkten besteht und beide die Zahl 20 ergeben, ist die Gestalt des A als 1. Buchstabe nach der oberen Spitze und das V als 20. Buchstabe nach der unteren Spitze gebildet.
VIII. DIE DOPPELRAUTE (I)
|
|
|
|
Als drittes Element lassen sich aus dem Dezimalstern drei Doppelrauten (DR)
herauslesen.
Damit vereint der Tetraktysstern drei verschiedene Figuren in einfacher (Tetraktysstern), doppelter (Tetraktys) und dreifacher (Doppelraute)
Ausführung.
Hier sei auf ein
weiteres Zahlenprinzip hingewiesen. Eine ungerade Zahl geht aus der Addition
von zwei nebeneinander stehenden Zahlen hervor (7+6=13), eine gerade aus der
Summe zweier Zahlen, die einer mittleren benachbart sind (6+4=10). Die beiden
Zahlen, die eine neue Zahl bilden, sollen Konstitutive oder konstitutive Zahlen
genannt werden. In den geometrischen Figuren des Tetraktyssterns ergibt die
Addition der Punkte + Dreiecke einen Zähler mehr als die Linien:
|
|
P |
D |
P+D |
L |
P+D+L |
|
GS |
|
DzStern |
13 |
12 |
25 |
24 |
49 |
*1 |
49 |
|
Tetrakt. |
10 |
9 |
19 |
18 |
37 |
*2 |
74 |
|
DR |
7 |
4 |
11 |
10 |
21 |
*3 |
63 |
|
|
|
|
|
|
|
|
186 |
Die Summe der 6 Figuren ist 6*31. Die Zahl 6 bedeutet die
Gemeinschaft der 3 Personen, 31 Einheit in der Dreiheit. Punkte, Dreiecke und Linien verhalten sich 54:42:90= 6*
[(9:7):15], wobei 9+7 die
konstitutiven Zahlen für 16 sind.
Die DR ist für das Verständnis des Dezimalsystems von besonderer Bedeutung.
Zunächst sollen einige numerische Fakten betrachtet werden. Jede Raute besteht
aus einem Rahmen von 4P u. 4L. Wie beim
Durchmesser haben wir wieder den doppelten Zählaspekt von 2 Einzelrauten und
einer Doppelraute. Die beiden Zählweisen ergeben 16+15=31, das ist der Durchschnittswert der 6 Figuren des Tetraktyssterns.
Jede Raute mit "Füllung" (Fläche, Linie, Fläche) besteht aus 11 Elementen. Bei doppelter Zählweise
der DR ergibt sich 22+21 = 43.
Die DR enthält drei Gruppen von Elementen, die mit den drei
Zählweisen des Dreiecks übereinstimmen: 4 Dreiecke (Flächen), 7Punkte, 10 Linien.
Bevor wir zur
eigentlichen Bedeutung der DR für das Dezimalsystem kommen, müssen wir die
Zahlen 1-10 in Form einer
Strecke betrachten. Wir verwenden dafür den Begriff Streckenmodell.
XI. DER OKTAEDER
|
|
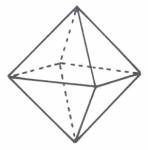
1. Bildet man
aus zwei DR ein Achsenkreuz, faltet die Mittellinien und verbindet
kreisförmig die äußeren Eckpunkte, entsteht ein Oktaeder mit den
Elementen 6P, 8D, 12L =26 Elemente, als 27. Element kann noch das Volumen
hinzutreten:
|
|
2. Ein Oktaeder
enthält über die vertikalen Spitzen hinweg 4 spiegelverkehrte Dreiecke mit je
13 Elementen, die doppelte Anzahl der Oktaeder-Elemente. Außerdem lassen sich 4
Rauten mit je 11 Elementen erkennen. 11 und 13 bilden eine Analogie zu den
Zahlen 1 u.3. Fügt man zum Additionsergebnis 4*(13+11)=96 noch das Volumen 1
hinzu, ergibt sich 961 = 31².
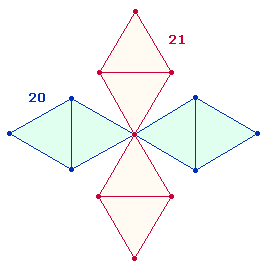
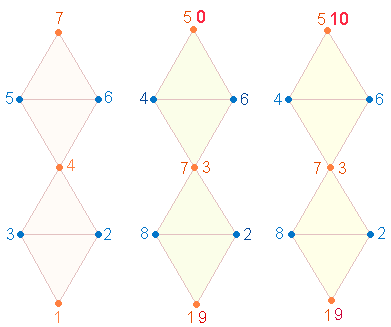
3. Den 3 DR des
Tetraktyssterns entsprechen 3 Zählweisen (obere Spitze 7, 5-0, 5-10). Verbindet man jede Zählweise mit jeder, lassen sich
drei Oktaeder bilden:
|
|
Durch Addition der ZW und Faktorenwerte (FW) erhält man ein
deutliches Zahlenverhältnis:
|
Zählg. |
7 |
5-0 |
5-10 |
Sm. |
|
ZS |
28 |
45 |
55 |
128 |
|
FS |
27 |
39 |
46 |
112 |
|
|
|
|
|
240 |
|
112:128 = 16*(7:8) |
||||
Zahlenverhältnisse zeigen sich auch zwischen den 3 Vertikal- und 2 Horizontalebenen:
|
|
vert. |
hor. |
|
|
ZS |
72 |
56 |
72:56 =
8*(9:7) |
|
FS |
63 |
49 |
63:49 =
7*(9:7) |
Die ZS und die FS verhalten sich
jeweils 9:7. Dieses Verhältnis spiegelt die
unterschiedliche Numerierungsweise wider: die lineare Numerierung besetzt 7 Punkte, die achtförmige 9 Positionen auf 7 Punkten. Die Zahlen 9+7 sind gleichzeitig die
Konstitutivzahlen ihrer Summe 16.
4.
Wichtige Zahlen, die den Oktaeder kennzeichnen, sind:
53: Von der unteren zur oberen
Spitze Zählt man 3 Punkte und 2 Linien = 5. Auf der Rückseite, die zum
Ausgangspunkt zurückführt, bleiben 3 Elemente (L+P+L) übrig. Die reale Zahl 53
setzt sich aus der Doppelzählung der 26 Oktaederelemente ohne Volumen und 26+1
= 27 Elemente mit Volumen zusammen. Entsprechend bezieht sich auch die Zahl 126
auf den Oktaeder.
58: Ähnlich wie 53 entsprechend
dem Verhältnis der Teilzahl zur ganzen Zahl.
151: Die Umrundung des Oktaeders
beginnt mit 1, erreicht mit 5 die Mitte und kehrt zum Ausgangspunkt 1 zurück.
158: Ähnlich wie 58 mit Nennung
des Ausgangspunktes.
5.
(September 2015) Mit
dem Oktaeder ergeben sich für das Dezimalsystem drei Figuren mit einer Dreizahl
von Achsen oder Seiten: drei Achsen des Hexagons, drei Seiten der Tetraktys und
drei quadratische Mittelbasen des Oktaeders:
|
|
Zu
unterscheiden ist die Einzelzählung und Ganzheitszählung der Elemente:
|
|
H |
T |
O |
sm |
FW |
sm |
|
E |
15 |
21 |
24 |
60 |
12 |
72 |
|
G |
13 |
18 |
18 |
49 |
14 |
63 |
|
|
28 |
39 |
42 |
109 |
26 |
135 |
|
72:63
= 9*(8:7) |
||||||
Das Verhältnis 9*(8:7) läßt sich auf den Zickzackdurchmesser
der Doppelraute beziehen mit 9 Durchmesserelementen, 8 Rahmenlinien und 7 Punkten der ganzen Doppelraute:
|
|
Erstellt: August
2001
Seither: mehrfach erweitert und
überarbeitet