Allgemeines über Achsenkreuze

I. Die Achsenkreuze AK2-9

Das Achsenkreuz AK2

II. Das numerierte Basisachsenkreuz mit Quadratbildungen

III. Verbindung von Zweiachsigkeit und Dreiachsigkeit

IV. Kreisförmige Numerierung von Quadratrahmen

s.a. Eigenschaften von Quadraten und Quadratrahmen

Die 18 Binnenquadrate des Qu5

In diesem und weiteren Beiträgen soll gezeigt werden, daß das Achsenkreuz genuiner Ausgangspunkt einer kreisförmigen und sich unendlich fortsetzenden Entfaltung der Zahlen ist und dem 5*5 Punkte Quadrat eine modellhafte Bedeutung zukommt.

I. Die Achsenkreuze AK2-9

1. Ein Achsenkreuz besteht aus zwei gleich langen Achsen, die im rechten Winkel zu einander stehen. Auch die 4 Kreuzarme sind gleich lang. Konstruktionsbasis ist der Kreis. Zu unterscheiden sind der Mittelpunkt als ungerader Beginn und die gerade Zahl symmetrischer Elemente, d.h. gleichviele Radialmaße (Linien) und (Begrenzungs-)Punkte.

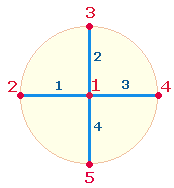
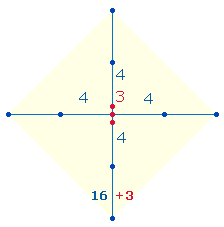
2. Das einfache oder Ur-Achsenkreuz besteht aus Mittelpunkt, 4 Radialmaßen und 4 Begrenzungspunkten, also aus 1+(4*2) = 9 Elementen. Es ist deshalb von besonderer Bedeutung, weil dem Dezimalsystem die (zählbaren) Grundzahlen 1-9 zugrunde liegen:

Der Zahl 1 des Mittelpunktes steht die Numerierungssumme 14 der äußeren Achsenpunkte gegenüber. Im SATOR-Quadrat entsprechen die beiden Zahlen den Buchstaben A und O auf den Randpunkten des äußeren Quadratrahmens. Die beiden Werte haben eine grundlegende Bedeutung in den 3-stelligen Umkehrzahlen 114 und 141, deren Quersumme 6 beträgt.

In analoger Weise kann die Numerierungssumme der Radiallinien hinzugefügt werden. Die zusammengesetzten Zahlen sind nun 124 und 241; die Quersumme der Einzelziffern ist 7. Beide Quersummen ergeben die Zahl 13.

3. Wenn das Basisachsenkreuz um ein Radialmaß erweitert wird, wächst die Zahl der Elemente um jeweils 8. Das nächst größere Achsenkreuz besteht demnach aus 9+8 = 17 Elementen.

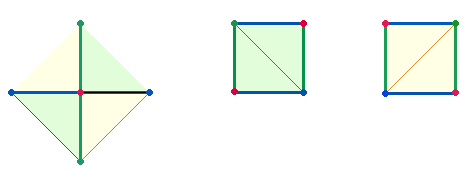
4. Verschiebt man einen Winkel eines Achsenkreuzes gegen den gegenüberliegenden, bis sich die Enden decken, erhält man ein QUADRAT. Geht man vom unteren Punkt des Achsenkreuzes aus, kann man den linken Winkel nach rechts und den rechten Winkel nach links verschieben. Man erhält so zwei Quadratbildungen.

Die Seitenlängen eines Quadrats bestehen aus so vielen Punkten, wie man vom Mittelpunkt aus zum Ende eines Achsenarmes zählt. Daher ist es sinnvoll, ein Achsenkreuz mit der Zahl der Punkte eines Achsenarmes zu bezeichnen. Das Basisachsenkreuz sei daher Achsenkreuz 2, abgekürzt AK2, genannt:

Entsprechend den Grundzahlen von 1-9 sind Achsenkreuze der Ordnung 2-9, also 8 konzentrisch wachsende, von besonderem Interesse. Dazu weitere Informationen

Jede der beiden Quadrate enthält eine Diagonale, die, zusammen mit einer zweiten ergänzten, einen Mittelpunkt erzeugt. Das diagonale Achsenkreuz scheint demnach dem Mittelachsenkreuz voranzugehen. Dieses liefert erst der Quadratrahmen (QR) des AK3 = QR3.

II. Das numerierte Basisachsenkreuz mit Quadratbildungen

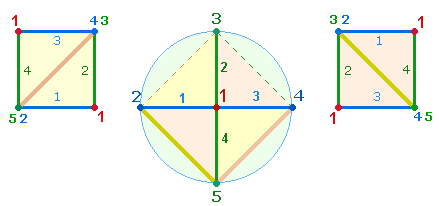
1. Die oben durchgeführte Numerierung des Basisachsenkreuzses kann auf die beiden Quadratbildungen übertragen werden:

Bei der Winkelverschiebung wandert die Eins des Mittelpunkts mit, sodaß die Numerierung des Quadrats zweimal die Eins enthält. Die Punktenumerierung des Achsenkreuzes und des dazugehörigen Quadrats kann als eine wesentliche Summeneinheit angesehen werden. Zu den zusammengesetzten Zahlen 114 und 141 kommen nun 214 und 142 hinzu. Letztere sind in den Umkehrformen 124 und 241 bereits in Erscheinung getreten. Durch Hinzufügung der Linienwerte erhält man 224 und 242; Die Quersummen der zusammengesetzten Zahlen sind nun 7+8 = 15.

Einen Beweis für die zweite 1 liefern die Faktorenwerte (FW) der Umkehrzahlen von 114:

Z	114	141	411	sm
FW	24	50	140	214

Die Punktezahl von Achsenkreuz und Quadrat ist 5+6 = 11 und unter Einschluß der Linien 9+10 = 19.

Weitere zusammengesetzte Werte ergeben sich aus dem Zusammenfall und der Addition von je zwei Numerierungspaaren. Aus 1+25+1 läßt sich 171 und aus 1+25+1+43 277 bilden. Dasselbe gilt für das zweite Quadrat: 151, 191, 259.

2. Die Numerierungssummen von Achsenkreuz und Quadrat betragen 15+16 = 31 und unter Hinzufügung der Linienwerte 25+26 = 51. Die Faktorenwerte (FW) der Zahlen 124, 241, 224 und 242 sind 35+241+17+24 = 317. Die Zahl 317 ist zu verstehen als 3*17 = 51.

Ein Achsenkreuz bringt also 2 Quadrate hervor. Die folgende Tabelle enthält die Numerierungssummen des Basisachsenkreuzes (BA) und der doppelt gerechneten Quadrate. Addiert werden ferner die Numerierungssummen der Punkte allein und der Punkte + Linien:

	BA	Qu*2	Sm.
P	15	32	47
P+L	25	52	77
	40	84	124
40:84 = 4*(10:21)

Die Endsumme 124 entspricht einerseits als Addition von 1+24 den Numerierungssummen der Punkte- + Linienwerte des Achsenkreuzes, andererseits zeigt sich in der Addition 12+4 das Gesetz zunehmender Quadratrahmenelemente, die an anderer Stelle behandelt werden: Jeder der 4 Eckpunkte des kleineren Quadratrahmens hat Bezug zu 3 Winkelpunkten des größeren. Das so entstehende Verhältnis ist 4*(1:3). Dies drückt sich sowohl in der Zahl 52 = 4*13 als auch in der Zahl 124 = 4*31 aus.

Die Zahlen 124, 214, 412, 421 haben Modellcharakter für das Quadrat schlechthin, indem sie das Verhältnis von Punkten (P) und Linien (L) je Quadratseite des Basisquadrats wiedergeben, z.B. 4*(2P:1L). Die FS der 6 Umkehrungen ergibt:

124	2* 2*31	35
142	2*71	73
214	2*107	109
241	241	241
412	2*2*103	107
421	421	421
1554		986
986=2*17*29>48

Die FS 986 ergibt den FW 48 = 4*12, wiederholt also die Grundstruktur des Quadrats.

III. Verbindung von Zweiachsigkeit und Dreiachsigkeit

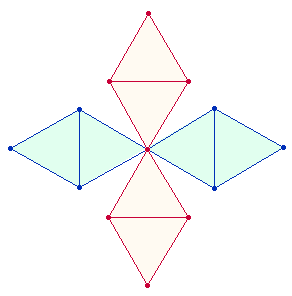
1. Achsenkreuze können über das AK9 hinaus beliebig weit konzentrisch ausgedehnt und zu zweidimensionalen Quadraten bzw. Quadratrahmen zusammengefügt werden. Aber nur die drei Achsen des Hexagon führen über den Tetraktysstern auf natürliche Weise zu einer dreidimensionalen Figur, zum Oktaeder, indem aus zwei Doppelrauten (DR) wiederum ein Achsenkreuz gebildet wird:

2. Der Tetraktysstern besitzt eine abgeschlossene Form. Kennzeichnend sind 9 Durchmesserelemente, die die Grundzahlen 1-9 repräsentieren. Die typische Zickzacklinie der DR stellt eine Erweiterung der Kreisachse um 2*2 Elemente dar, die den 4 Elementen der zweiten (vertikalen) Achse des AK2 entspricht. Sie ist durch den Mittelpunkt ebenso geteilt zu denken wie zuvor die beiden Radien der Kreisachse. Wiederum sind durch den gemeinsamen Mittelpunkt (MP) zwei radiale Mittelpunkte verdeckt, die durch 3 MP des nächst höheren Achsenkreuzes AK3 dargestellt werden. (Eine Achse des AK3 besteht ebenso aus 9 Elementen wie die Zickzacklinie der DR.) Setzt man die Summe der symmetrischen Elemente und die 3 MP zusammen, erhält man die Primzahl 163. Deren Einzelziffern wiederum geben die Punkteverteilung eines Tetraktysdreiecks wieder: MP, 6 Hexagonalpunkte und 3 Eckpunkte.

3. Während die Dreiachsigkeit ihr Ziel mit dem Tetraktysstern offenbar erreicht hat, ist das zweiachsige Achsenkreuz gegen unendlich ausdehnbar. Seine besondere Bedeutung liegt, wie oben bereits ausgeführt, darin, daß durch Verschiebung eines Winkels gegen den anderen ein Quadratrahmen gebildet werden kann. Quadratrahmen verschiedener Größe können konzentrisch angeordnet werden.

IV. Kreisförmige Numerierung von Quadratrahmen

1. Wenn nun konzentrische Quadratrahmen, beginnend vom Kreismittelpunkt, fortlaufend numeriert werden können, entsteht ein sich konzentrisch ausweitendes dichtes regelmäßiges Netz von Zahlen.

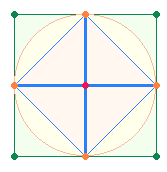
Für die Erstnumerierung wirkt das AK2 mit dem AK3 zusammen. Die im Kreis stehenden 4 Eckpunkte des AK2 lassen sich durch Linien zu einem Rautenquadrat verbinden. Auf dieses Ausgangsquadrat wird sodann ein Quadratrahmen des AK3 gesetzt:

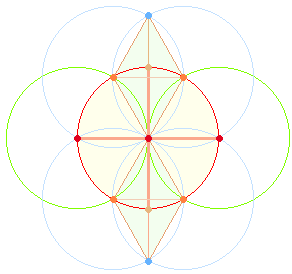
Die Konstruktion eines AK2 erfolgt wohl am natürlichsten über die Dreiachsigkeit, wenn hierzu der Radius des Ausgangskreises nicht verändert werden soll: Von den beiden Kreislinienpunkten der Kreisachse aus schlägt man je einen Kreis und erhält 4 Schnittpunkte auf der Kreislinie. Diese sind Ausgangspunkte für weitere Kreise und zwei Schnittpunkte außerhalb des Kreises, die man durch eine Gerade miteinander verbindet. Verbindungslinien zu den Kreislinienpunkten und dem Mittelpunkt nehmen bereits die Figur der Doppelraute des Tetraktyssterns vorweg:

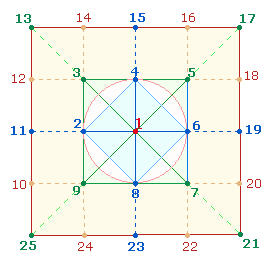
2. Es zeigt sich, daß eine kreisförmige Numerierung des Quadrats vom MP aus – im Unterschied zur Numerierungsmöglichkeit des Achsenkreuzes – nur durch Besetzung der Punkte möglich ist, da nicht alle Linien erfaßt werden könnten. Die natürlichste Richtung vom Mittelpunkt aus ist die entlang der Horizontalachse mit nachfolgender Rechtswendung:

Das Rautenquadrat des Ausgangs setzt seine strukturelle Bedeutung in weiteren Rahmenquadraten fort.

Ausgangspunkt einer weiteren Numerierungsmöglichkeit, auf die hier nicht eingegangen wird, wären die 4 Punkte eines Quadrats ohne Mittelpunkt.

3. Die 4 Achsen des ersten Quadratrahmens QR3 werden mit jedem neuen Quadratrahmen um 4 Achsen + der bereits vorhandenen Achsen erweitert. Als Quadratrahmen eignen sich lediglich Achsenkreuze mit ungeraden Zahlen, da die geraden nach Umwandlung in ein Quadrat keinen Mittelpunkt, sondern ein "Mittelquadrat" besitzen.

Die Bezeichnung für die Achsenkreuze AK und die Quadratrahmen QR ist jeweils gleich. Dem AK5 entspricht also ein QR5.

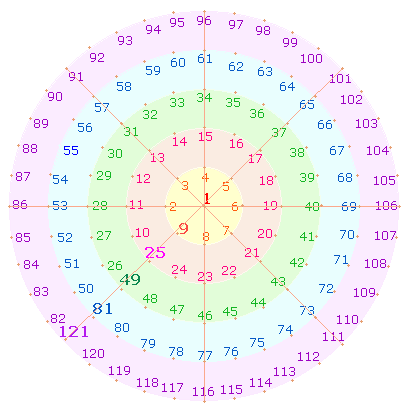
4. Die Axiallinien eines QR lassen sich auf einen Kreisbogen ausdehnen, den man durch die 4 diagonalen Eckpunkte gezogen hat. Entlang den Schnittpunkten auf der Kreislinie trägt man dann die fortlaufenden Zahlen ein. Es entstehen so konzentrische Zahlenkränze:

5. Die kreisförmige Numerierung konzentrischer Quadratrahmen kann als ein dynamischer Vorgang angesehen werden, der sich in Unermeßliche erstreckt. Sie ist vielleicht Grundmodell eines Entwicklungsprinzips, das in der Urknalltheorie und der Ausdehnung eine Bestätigung findet. Auf diese Weise haben alle Zahlen ihren festen Platz.

Erstellt:Januar 2008, März 2008

index