36:36
zweistellige Umkehrzahlen im Verhältnis 4:7
I.
Zahlensummen
II.
Zahlensummen und Faktorensummen
III.
Bedeutung der Zahlen 4
und 7
IV.
72 Umkehrzahlen im Sechseckstern und zwei Tetraktys
III. Bedeutung der Zahlen
4 und 7
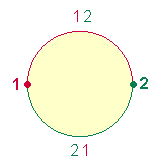
1. Die Umkehrzahlen 12 und 21 begründen das Verhältnis 4:7 aller 36 Zahlenpaare. Um die Bedeutung dieses Verhältnisses gebührend zu erfassen, ist es günstig, von zwei Kreisbogenhälften auszugehen, deren zwei Schnittpunkte mit 1 und 2 bezeichnet werden:
|
|
Die erste Kreisbogenhälfte verläuft von 1 zu 2, die zweite kehrt spiegelbildlich von 2 zum Anfang 1 zurück. Was in der ersten Hälfte begonnen wird, wird in der zweiten vollendet. Das heißt, in der Zahl 21 wird der Verhältnisfaktor 4 wiederholt und durch 3 zu 7 erweitert.
Von der Teilung des Kreises in zwei Hälften geht jede weitere Differenzierung aus, entweder zweiachsig oder dreiachsig.
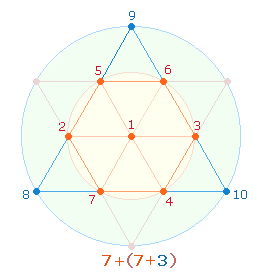
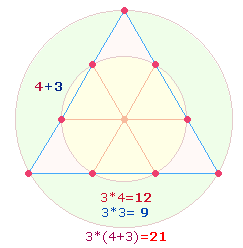
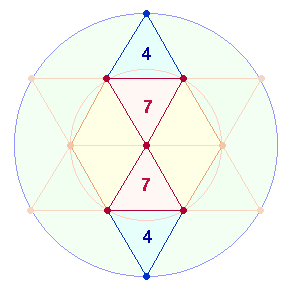
2. Die Faktoren 3*4 und 3*7 der beiden Umkehrzahlen 12 und 21 spiegeln in ihrer Addition die 7 Punkte des Hexagons und dessen Erweiterung die 10 Punkte der Tetraktys wider:
|
|
Die Grafik zeigt zwei Tetraktys innerhalb zweier konzentrischer Kreise, deren Kreisflächenverhältnis 1:3 beträgt und analog durch 7 und 10 Punkte wiedergegeben wird, während 7 zu 3 Punkten das Flächenverhältnis 1:2 entspricht. Die beiden Flächenverhältnisse, deren Addition 4+3 = 7 beträgt, sind grundlegend für viele andere Zahlenzusammenhänge. Theologisch sind sie als trinitarische Verhältnisse zu verstehen.
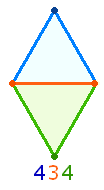
3. Das Inklusionsprinzip der 4 in der 7 zeigt sich in den Elementen der drei Tetraktysseiten, wobei die Punkte der oben gezeigten ersten Kreisbogenhälfte entsprechen: Jede einzelne Seite besteht aus 4 Punkten und 3 Linien:
|
|
Daß die drei Tetraktysseiten in dieser Weise zu verstehen sind, ist aus der Faktorensumme (FS) 108 = 12*9 der Zahlen 12 bis 21 zu erschließen:
|
ZW |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
165 |
|
FW |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
108 |
|
273 = 13*21 |
273 |
||||||||||
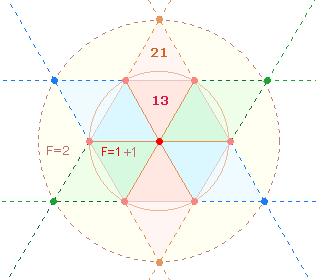
Die Einzelziffern des Produkts 13*21 zeigen die oben erläuterten trinitarischen Kreisflächenverhältnisse. Sie beziehen sich auf die "Konkurrenzfigur" der Tetraktys, auf die Doppelraute (DR):
|
|
Die Grafik zeigt in der Mitte zwei sanduhrförmig zusammenstoßende Dreiecke, die nach oben und unten um je ein weiteres Dreieck erweitert werden, wodurch zwei Rautenfiguren entstehen. Die 13 Elemente des hexagonalen Doppeldreiecks und die 21 Elemente der gesamten Doppelraute geben das Kreisflächenverhältnis 1:3 wieder.
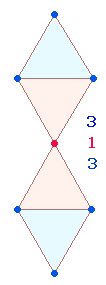
4. Die Doppelraute hat eine ebenso große Bedeutung wie die Tetraktys. Denn aus einem DR-Kreuz läßt sich die dreidimensionale Figur des Oktaeders bilden, der als das Endziel der Dreiachsigkeit anzusehen ist. Daher ist die RAUTE die zentrale Figur der Zahlen 4 und 7. Im Dreieck kommen 3 Punkte und 3 Linien zu ihrem ersten zweidimensionalen Abschluß. Es besteht aus 7 Elementen und hat daher wesentlich trinitarische Bedeutung. Punkte und Fläche sind einander zugeordnet, sodaß man das Verhältnis 4:3 oder 3:1:3 bilden kann. Letzteres ist auch im Punktemuster der DR zu erkennen.
|
|
Im Hexagramm kommt die Rautenfigur zustande, indem die 7 Elemente eines einzelnen Dreiecks um 4 Elemente erweitert werden:
|
|
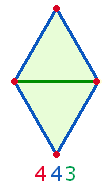
5. Der Vorgang der Vollendung der Raute stellt sich nun, im Vergleich zur ersten der beiden Kreisbogenhälften, als Umkehrverhältnis dar, denn 7 ist die Ausgangszahl der Elemente, zu denen 4 hinzukommen. Das Kreisflächenverhältnis 1:2 hingegen entspricht der ersten Kreisbogenhälfte. Andererseits, wenn die zweite Kreisbogenhälfte die Gestalt 21 hat, so ist auch im Hexagramm eine Umkehrbewegung von außen nach innen gefordert: Die Umkehrbewegung strebt auf die hexagonale Kreismitte zurück. Dies ermöglicht auch einen zweiten Blick auf die Raute. Die 4 Elemente des Erweiterungsrings (1 Punkt, 2 Linien, 1 Fläche) sind spiegelbildlich auch im Ausgangsdreieck vorhanden, zu dem – als Vollendung 4+3 – die gemeinsame Mittellinie (1 Punkt, 1 Linie, 1 Punkt) hinzukommt. Ebenso denkbar ist die Gemeinsamkeit von 4 Punkten, 4 Linien und 3 Binnenelementen (1 Fläche, 1 Linie, 1 Fläche):
|
|
|
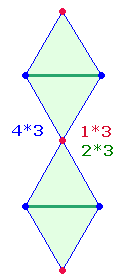
6. Dem Kreisflächenverhältnis 2:1 entsprechen 21 Elemente der DR. Diese können wie die drei Tetraktysseiten in 12+9 Elemente aufgeteilt werden:
|
|
Im Unterschied zu den drei Tetraktysseiten bilden nicht 3*4 Punkte, sondern die 4*3 Dachelemente (1 Linie, 1 Punkt, 1 Linie) die Ausgangslage. Die Vollendung der DR zeigt sich in der Hinzunahme der 9 Binnenelemente.
7. Welche neuen Zusammenhänge sich mit der Innenbewegung des Kreisflächenverhältnisses 2:1 bieten, zeigt der nächste Beitrag, worin die 72 Umkehrzahlen in Rautenform angeordnet sind und nach dem Vorbild der zwei Tetraktys verschränkt werden.
Erstellt: September 2014