Quadratstruktur im 5x5 Punkte-Quadrat
I.
Quadratstrukturen
1.
Zu
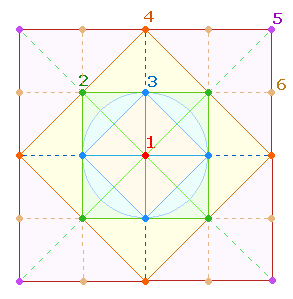
unterscheiden sind Rautenquadrate (RtQ) und horizontal-vertikale Vollquadrate (VQ). Ein Vollquadrat hat die doppelte
Fläche des von ihm umgrenzten Rautenquadrates. Beiden Quadraten liegt ein
Basisachsenkreuz AK2
zugrunde.
Ein RtQ besteht aus 5, ein VQ aus 9 Punkten. Vom Mittelpunkt aus
lassen sich beide Quadratformen horizontal und vertikal um einen Punkt
verschieben, sodaß jeweils 4
Quadrate zustande kommen:
|
|
Ebenfalls jeweils 4 Quadrate erhält man, wenn man das
mittlere Quadrat diagonal um einen Punkt verschiebt:
|
|
2.
Ist
ein 5x5 Punkte-Quadrat (Qu5) numeriert, kann man die Werte der
2*(1+4+4) Quadrate errechnen. Dabei kann
man sich der 6
symmetrischen Punktegruppen bedienen:
|
|
Für die insgesamt 18 Quadrate mit insgesamt 126 Punktepositionen gilt es nun, die
Häufigkeit jeder Punktegruppe zu ermitteln:
|
|
Rautenquadrate |
|
|||||
|
Gruppe |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl d. Positionen |
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
1 Qu. Mitte |
1 |
|
1 |
|
|
|
|
|
4 Qu. hor.vert. |
4 |
2 |
1 |
1 |
|
|
|
|
4 Qu. diagonal |
|
1 |
2 |
|
|
1 |
|
|
Sm. |
5 |
3 |
4 |
1 |
|
1 |
|
|
Hf.*Pos. |
5 |
12 |
16 |
4 |
|
8 |
45 |
|
|
Vollquadrate |
|
|||||
|
Gruppe |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl d. Positionen |
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
1 Qu. Mitte |
1 |
1 |
1 |
|
|
|
|
|
4 Qu. hor.vert. |
4 |
2 |
3 |
1 |
|
1 |
|
|
4 Qu. diagonal |
4 |
1 |
2 |
2 |
1 |
1 |
|
|
Sm. |
9 |
4 |
6 |
3 |
1 |
2 |
|
|
Hf.*Pos. |
9 |
16 |
24 |
12 |
4 |
16 |
81 |
|
gesamt |
14 |
7 |
10 |
4 |
1 |
3 |
|
3.
Das
Quadratpaar besteht aus 5+9
Punkten. Seine Elemente verteilen sich wie folgt:
|
|
P |
L |
F |
Sm. |
|
RtQ |
5 |
8 |
4 |
17 |
|
VQ |
9 |
12 |
4 |
25 |
|
|
14 |
20 |
8 |
42 |
Das Verhältnis der Punkte zur Zahl der Linien + Flächen ist 14*(1:2). Die Gesamtzahl der
Quadratelemente ist somit 9*42 bzw. 3*126
= 378. Die Zahl 378 ist die Summe der Zahlen von 1-27.
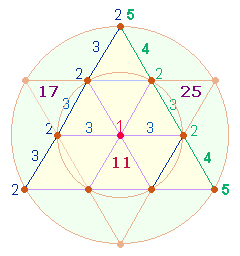
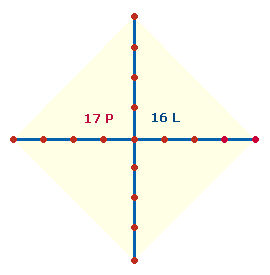
Die Zahlen 17, 25 und 378 sind von Bedeutung für den Tetraktysrahmen. Dieser besteht aus 9 Punkten und 9 Linien, eine einzelne Seite
jedoch aus 4 Punkten und 3 Linien. Dadurch kommen zwei
Zählungen zustande: 2*9 = 18, 3*7 = 21. Das Produkt 18*21 ergibt 378.
Durch zwei Numerierungsweisen
erhält man je Tetraktysseite die Summe 17 und 25:
|
|
Die
Numerierungssummen mal drei genommen ergibt wiederum die Zahl der 126 Punktepositionen. Diese Summe
verdoppelt sich auf 252
bei zwei Tetraktys.
4.
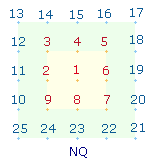
Numeriert
man ein 5*5 Punkte Quadrat von 1-25, ist die Durchschnittszahl 13. Der Wert für das Quadratpaar ist
somit 14*13
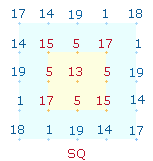
= 182. Die Zahl 182 ist der Zahlenwert (ZW) der Wörter SATOR OPERA TENET im SATOR-Quadrat und der Namen IESUS CHRISTUS.
Die genannte Beziehung zur Tetraktys zeigt sich in der
Sonderuntersuchung zum "magischen
Quadrat" der Kreuzesinschrift.
II. Einheit von
3+1 Quadraten
Die Einheit von drei Quadraten und dem magischen Quadrat der Kreuzesinschrift erweist sich
auch bei der Ermittlung der 18
Quadratwerte. Auf Differenzierungen soll hier verzichtet werden. Es handelt
sich um nachstehende Quadrate:
|
|
|
|
|
Die folgenden Tabellen enthalten die
Zahlensummen (ZS)
und Faktorensummen (FS) der 6
symmetrischen Gruppen:
|
|
5*5 Qu |
|
|
1x1 |
|
||||||||||
|
Gr |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
ZS |
1 |
24 |
20 |
68 |
76 |
136 |
325 |
|
5 |
20 |
0 |
20 |
20 |
40 |
105 |
|
FS |
1 |
21 |
17 |
61 |
50 |
70 |
220 |
|
5 |
18 |
0 |
20 |
14 |
32 |
89 |
|
|
SATOR-Qu |
|
|
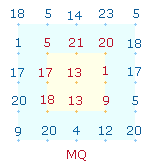
MQ |
|
||||||||||
|
Gr |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
ZS |
13 |
64 |
20 |
76 |
70 |
60 |
303 |
|
13 |
52 |
52 |
52 |
52 |
104 |
325 |
|
FS |
13 |
50 |
20 |
76 |
50 |
40 |
249 |
|
13 |
28 |
41 |
47 |
28 |
67 |
224 |
Die Werte werden nun mit dem
Häufigkeitsfaktor der symmetrischen Gruppen multipliziert:
|
Gr |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Hf. |
14 |
7 |
10 |
4 |
1 |
3 |
|
|
5*5 |
14 |
168 |
200 |
272 |
76 |
408 |
1138 |
|
1x1 |
70 |
140 |
0 |
80 |
20 |
120 |
430 |
|
SQ |
182 |
448 |
200 |
304 |
70 |
180 |
1384 |
|
|
|
|
|
|
|
|
2952 |
|
2952 = 9*8*41 |
|||||||
Die Summe für das SATOR-QUADRAT 1384 = 8*173 stimmt in der
Aufteilung 13+84 überraschend mit
der ZS des Mittelpunktes und der 8 Rahmenpunkte überein. Für das darübergelegte
Rautenquadrat kommen 4*19 = 76 hinzu, sodaß es
die Zahlensummen 97+76 = 173 hat.
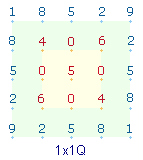
Das "magische
Quadrat" der Kreuzesinschrift hat für jede Symmetriegruppe den
Durchschnittswert 13.
Dieser kann mit den 126
Punktepositionen multipliziert werden. Das Ergebnis aller vier Quadrate ist
dann
2952+1638 = 4590 = 270*17 = FW 16+17 = 33.
Der Zahl 33 entspricht das Achsenkreuz AK5.:
|
|
Erstellt: April 2008