zurück

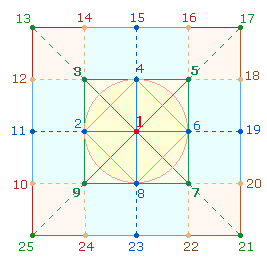
Das numerierte 5*5 Punkte Quadrat (3)

VI. Die Winkelpunkte

a) Zahlensummen

1. Die Zahlensumme (ZS) der 4 Eckpunkte und 8 Randpunkte ist 76+136 = 4*19 + 8*17 = 212 = 4*53. Die durchschnittliche ZS je Ecke und 3 Punkte ist also 53.

Die Einzelziffern der Zahl 212 weisen auf die 5 Punkte des einfachen Achsenkreuzes hin, numeriert von 1-5 ist die Summe das 3-fache von 5.

Schon im vorherigen Kapitel wurden die Zahlen 5 und 3 den Radialelementen des Doppelkreises des Tetraktyssterns zugeordnet. Sie stehen für das Flächenverhältns 3:1 der beiden konzentrischen Kreise. Fügt man die Summe 24 der Eckpunkte des inneren Quadratrahmens (QR) zu 212 hinzu, erhält man mit 236:4 = 59 einen Durchschnittswert, dessen Einzelziffern den Durchmesser-Elementen des inneren und äußeren Kreises entsprechen und das Flächenverhältnis 1:3 bedeutet.

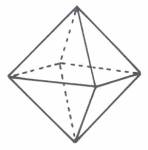
2. Die Zahl 212 ist auch in einer anderen Hinsicht von Bedeutung. Aus einem Achsenkreuz von 2 Doppelrauten (DR) läßt sich ein Oktaeder zusammenfügen:

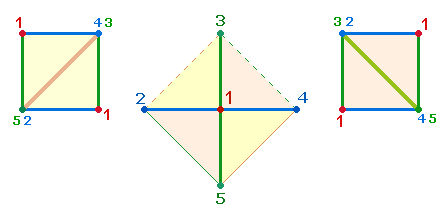
Ein Oktaeder besteht aus 26 Elementen, die sich durch das neue Element des Volumens auf 27 erhöhen. Beide Summen ergeben 53. Die zweifach sinnvolle Numerierung der DR-Elemente von 1-4 und 1-6 und ihre konsequente Übertragung auf die Oktaeder-Elemente (einschließlich Volumen = 5 und 7) führt zu einer Dreifachzählung mit den Summen 27+84+101 = 212.

3. Die Zahlen 19 und 17 in der Zusammensetzung 10+9 und 9+8 sind trinitarisch komplementär zu 1+2. Ebenfalls komplementär zu verstehen sind 19 Punkte des Achsenkreuzes AK5.

Auch hinsichtlich des Oktaeders kommt ihnen eine gewisse Bedeutung zu: Teilt man den Oktaeder an seiner quadratischen Basis, verdoppeln sich deren 8 Elemente und man erhält zwei Hälften aus 9+8 = 17. Durch die Hinzufügung der neu entstandenen Basisfläche und des Volumens erhöht sich die Zahl um 2 Elemente je Hälfte: 17+2 = 19.

b) Faktorensummen

1. Die Faktorensummen (FS) der 4 Eckpunkte (EP) und 8 Randpunkte (RP) des QR5 sind 50+70 = 120, ihr Verhältnis 10*(5:7).

Die Zahlen 5 und 7 sind die regulären Konstitutiven ihrer Summe 12. Sie haben ihre Modelle in den 5 DM-Elementen der Kreisachse und den 7 Elementen einer Tetraktysseite. Als Verhältnis des Teils zum Ganzen bedeuten sie 5 Punkte des hexagonalen DR-Anteils und der Gesamtzahl von 5+2 = 7 Punkten der Doppelraute. Aus 10 Punkten besteht die Tetraktys und 10 Linien die DR.

2. Die 12 Zahlen der Winkelpunkte haben also den durchschnittlichen Faktorenwert (FW) 10. Die Zahl 120 weist mit den Faktoren 4*3 und 2*5 in vollkommener Weise auf die Bildung des Quadrats aus dem numerierten Achsenkreuz hin, wie bereits im vorigen Kapitel gezeigt wurde:

Nach Addition der Faktoren (s.li.Grafik) erhält man die umlaufende Zahlenfolge 717 bzw. 171. Erstere läßt sich aus der FS 71 der 8 Eckpunkte des QR5+QR3 und der FS 70 der 8 Randpunkte erkennen. Die Zahlen 71+70 sind konstitutiv für ihre Summe 141 = 3*47. Die Zahl 141 ist in 14+1 aufteilbar und gibt so die Achsenkreuznumerierung wieder.

Die Zahl 347 ist der ZW der lateinischen Namen der Dreifaltigkeit: PATER (57) FILIUS (73) SANCTUS SPITRITUS (217).

c) Zahlensummen + Faktorensummen

1. Die ZS+FS der 4*3 Winkelpunkte ist 212+120 = 4*(53+30) = 4*83 = 332. Die Einzelziffern der beiden Summen bestehen aus 2 und 1 und in ihrer Summe tritt wiederum das Verhältnis 5:3 hervor. Es stimmt mit dem Aufbau des 5*5 Punkte-Quadrats aus dem QR3 und QR5 überein.

Je 3 Zahlen einer Ecke haben also die ZS+FS 83. (Tatsächlich handelt es sich um (4*2)*3 Werte.) Die Konstitutivzahlen für 83 sind 41+42. Deren FS 41+12 = 53 deckt sich auffällig mit der Verhältniszahl 53 aus der ZS 212. Das Differenzverhältnis zwischen FS 53 und restlicher ZS 83 ist 53:30. Aus den Einzelziffern der beiden Verhältniszahlen kann man eine Aufteilung in 5 DM-Elemente und 3+3 Radialelemente der Kreisachse feststellen. Ein solcher Doppelaspekt liegt offensichtlich auch bei der Umwandlung eines Achsenkreuzes in ein Quadrat vor: Die Zahl 1 des Mittelpunktes bleibt beiden Winkeln des Quadrats erhalten. Das Achsenkreuz besteht also aus 4+1, das Quadrat aus 4+2 Numerierungswerten.

Diese Sichtweise scheint die ZS+FS der Zahlen 1-12 zu bestätigen: 78+64 = 142. Wie der FW von 12 = 3*4 ist die Summe der Einzelziffern 1+4+2 = 7.

2. Der Bezug der Zahl 12 zum Quadrat ist also offensichtlich: Jede Seite des Quadrats besteht aus 3 Elementen: 2 Punkten und 1 Linie.

3. Die Umkehrzahl 124, aufteilbar in 12+4 = 4*(3:1) = 16, zeigt die Beziehung zwischen je 3 Winkelpunkten zu einem Eckpunkt des jeweils kleineren QR. Dieses Verhältnis wird auch deutlich in der Addition der beiden Zählungen: 15+16 = 31.

Erstellt:Januar 2008

index