Die Zahl 137
1.
Die Wissenschaft hat das Alter des Weltalls auf 13,7 Milliarden Jahre errechnet. Wie diese
Zahl im Dezimalsystem grundgelegt ist, soll in einigen Aspekten und Modellen
aufgezeigt werden.
2.
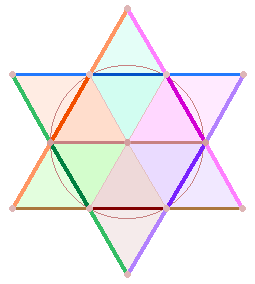
Das Hauptmodell des Dezimalsystems ist der Tetraktysstern,
der aus der Verlängerung der Segmentlinien des Hexagon entsteht:
3.
Die Tetraktys ist durch Pythagoras in die Geschichte der
Mathematik eingeführt worden. Sie ist ein Zahlendreieck, dessen Punkte sich von
1 bis 4 erweitern und die Summe 10 ergeben:
|
|
Wie die 10 Punkte, so kann man auch die
übrigen Elemente der Dreiecksfigur zählen: 18 Linien und 9 Dreiecke. Die Gesamtzahl der Elemente ist 37. Tatsächlich spiegeln die beiden
Einzelzahlen den Aufbau der Tetraktys wider: 3 Eckpunkte und 7 Hexagonpunkte.
Im Tetraktysstern stehen einander
gegenläufig zwei Tetraktys gegenüber. Das ergibt die doppelte Zahl 74 von Elementen.
1.
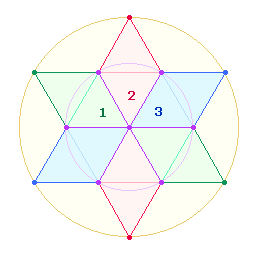
Der Tetraktysstern läßt sich auch in drei geometrische
Figuren einteilen, die Doppelraute (DR) genannt werden soll. Sie besteht aus 7 Punkten, 10 Linien und 4 Dreiecken, zusammen aus 21 Elementen:
|
|
Die Gesamtzahl der DR-Elemente ist
also 63.
Zusammen mit den 74
Elementen der beiden Tetraktys ergeben sich somit 137 Elemente.
2.
Will man dem Tetraktysstern ontologische Relevanz d.h.
göttliche Abbildhaftigkeit zumessen, so wird man an die Einheit der drei
göttlichen Personen denken. Sie scheint auf verschiedene Weise auf, z.B. durch
Verrechnung der Zahlenwerte (ZW) 74 und 63 mit ihren Faktorenwerten (FW):
|
ZW |
74 |
63 |
137 |
|
FW |
39 |
13 |
52 |
|
39:13 = 13*(3:1) |
|||
Die beiden Faktorenwerte verhalten
sich zueinander wie 3:1.
3.
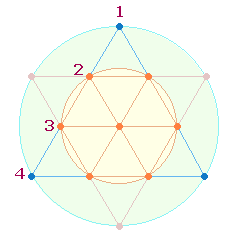
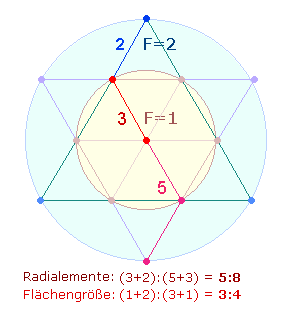
Zieht man um die äußeren Schnittpunkte eine Kreislinie, so
verhält sich die Fläche des inneren Kreis zum äußeren wie 1:3:
|
|
Die beiden konzentrischen
Kreisflächen sind ein weiterer trinitarischer Hinweis.
Das Dezimalsystem ist ein solches Sinngefüge
von Zahlen, daß Bedeutungen auch in Zusammensetzungen erhalten bleiben. So
weisen auch die 13
Punkte des Tetraktyssterns für sich allein bereits auf den einen Gott in drei
Personen hin. Sie stehen aber auch für die Flächengröße 3 wie die 7 Hexagonpunkte für die
Flächengröße 1. Auf diese Weise lassen sich die beiden Punktezahlen zu 137 zusammensetzen.
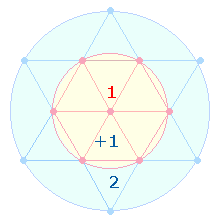
4. Eine Zusammensetzung
ergibt sich aus folgender Überlegung: Die Flächen der beiden konzentrischen
Kreise werden aufgeteilt in die Größe 1 des Hexagon. Durch den zweiten Kreisbogen kommt ein
Flächenring von weiteren 2
Einheiten hinzu. Andererseits aber besitzt der größere Kreis seine
Eigenberechtigung und so fügen sich zur Flächeneinheit 1 des Hexagonkreises die Einheiten 3 des äußeren Kreises hinzu. Aus
der Addition dieser vier Flächeneinheiten ergibt sich die Zahl 7.
Den Flächengrößen der Kreise kann
man die Zahl ihrer Radialelemente zuordnen: dem Hexagon 3, dem Kreisring 2 und dem äußeren Kreis 5. Daraus ergibt sich (3+2)+(3+5) = 5+8 = 13. Nun läßt sich die Zahl der
Radialelemente und der Flächeneinheiten zu 137 zusammensetzen:
|
|
5.
Das Zahlensystem ist als eine Entfaltung größerer Zahlen
aus der Addition von jeweils zwei angrenzenden kleineren Zahlen zu verstehen.
Die Zahl 137 konstituiert sich demnach aus 69+68. Auch hier bietet der
Tetraktysstern ein Modell: Das Hexagon besteht aus drei Achsen und jeweils 5 Durchmesserelementen.
Andererseits besteht jeder der beiden Radien einer Achse aus 3 Elementen, woraus sich 6 Radialelemente je Achse ergeben.
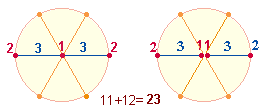
Numeriert man diese Elemente, indem man dem Mittelpunkt die Zahl 1, den Kreislinienpunkten die Zahl 2 und der Radiallinie als
Verbindung zwischen beiden die Zahl 3 zuweist, erhält man die Summen 11+12 = 23, und mit 3 multipliziert die Zahl 69:
|
|
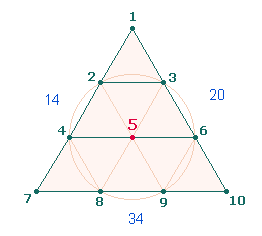
Die drei Hexagonachsen werden in der
Tetraktys gewissermaßen zu drei Dreiecksseiten geordnet. Zählt man die
Numerierung jeder Seite, erhält man die Zahl 68:
|
|
Einschränkend ist zu bemerken, daß
beide Zählweisen inkongruent sind: Die Hexagonachsen werden zweimal gezählt,
mit denselben Zahlen von 1-3 und unter Einbeziehung der Radiallinien. Eine
gewisse Inkongruenz ist vielleicht dann rational verträglich, wenn, wie hier,
zwei geometrische Konstruktionen vergleichbar und einander zugeordnet sind und
die Ergebnisse zusammenstimmen.
6.
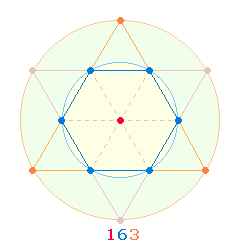
Eine weitere Zusammensetzung der Zahl 137 aus 73+64 ergibt sich aus dem Aufbau der Tetraktys: 7 Hexagonpunkte geben 1 Flächeneinheit wieder, die drei
Eckpunkte die 2 Flächeneinheiten des Kreisrings. Auch den 6 Kreislinienpunkten des Hexagon
entspricht 1
Flächeneinheit, dem Mittelpunkt und den 3
Eckpunkten jedoch 3 Flächeneinheiten:
|
|
Auf diese Weise wird eine
Aufteilung der Zehner- und Einerziffern vorgenommen in 13 Punkte des Tetraktyssterns und 7 Flächeneinheiten.
7.
Eine einzelne Raute besteht aus 11 Elementen: 4 Punkten, 5 Linien und 2 Dreiecken, eine Doppelraute aus 22 Elementen, wenn man den
Mittelpunkt für jede Raute zählt, aus 21, wenn man für beide Rauten nur einen Mittelpunkt annimmt.
Der Tetraktysstern besteht somit
aus 6 einzelnen Rauten. Die Zahl 137 ergibt sich nun aus der Summe der
Faktorenwerte der durch 11 teilbaren Zahlen von 11 bis 99: Die Faktorensumme der Zahlen 1-9 ist 39; da die Zahl 1 bei der Primzahl 11 nicht gerechnet wird, bleibt 38 übrig: 9*11 = 99+38 = 137. Die Additionsreihe der FW ist also: 11+13+14+15+16+16+18+17+17
= 137.
8.
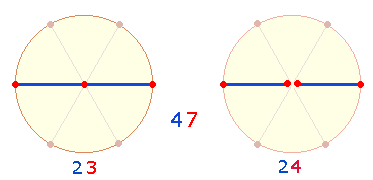
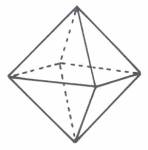
Aus 3*137 = 411 bestehen die FS 201+210 der Zahlen 1-23 und 1-24. Die Einzelziffern von 411 weisen sowohl auf 4+2 Radialelemente der Kreisachse hin als auch auf 4 Ecken der quadratischen
Mittelbasis des Oktaeders und seiner oberen und unteren Ecke:
|
|
|
Erstellt: Januar 2009