zurück

weiter

Die Zahl 153 im Johannesevangelium 21,11 (II)

C. 153 und lateinisch PISCIS

In diesem Beitrag sollen zunächst der Zahlenwert (ZW) von PISCIS und die Zusammensetzung seiner Buchstaben, dann die zugrunde liegenden Modelle untersucht werden.

I. Zusammensetzung und ZW von PISCIS

II. Zahlen- und Faktorensummen der Zahlen 1-17

III. PISCIS in der Doppelraute

a) Zwei Numerierungen

b) Fisch mit Rückgrat

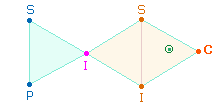
e) Zwei Fische in der Doppelraute

f) Dreimal ICHTHYS, einmal PISCIS

g) PISCIS und ICHTHYS als Fischfiguren

D. PISCIS – HOMO, MARE – TERRA

I. Zusammensetzung und ZW von PISCIS

1. Die 6 Buchstaben von PIS-CIS sind in zwei Hälften aufteilbar und zeigen am Ende jeder Hälfte die Buchstabenverbindung IS. Die ZW der Buchstaben P C, die den Anfang jeder Hälfte bilden, sind 15 und 3, ergeben also zusammengesetzt 153.

2. Der Gesamt-ZW stellt sich folgendermaßen dar:

P	I	S	C	I	S
15	9	18	3	9	18
15	27		3	27		72
42			30
42:30 = 6*(7:5)

Auffallend ist die Umkehrung der beiden ZW 27 zu 72. Auf das Verhältnis 7:5 ist später zurückzugreifen.

3. Die Zahl 17 ist im ZW 72 durch das Produkt 9*8 vertreten.

II. Zahlen- und Faktorensummen der Zahlen 1-17

1. Nicht nur die Zahlensumme (ZS), sondern auch die Faktorensumme (FS) der Zahlen 1-17 ist durch 17 teilbar. Das FS:ZS-Verhältnis beträgt 17*(7:9) = 17*16 = 272. Im Summenergebnis erkennt man die für den ZW von PISCIS charakteristische Umkehrung von 27 zu 72. Auch das interne Differenzverhältnis von FS zur ZS beträgt 7:2.

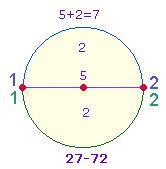
2. Den Umkehrzahlen 2 und 7 liegt unter anderem die Kreisteilung durch eine Durchmesserlinie/Achse zugrunde. Die 5 Elemente des Kreisdurchmessers teilen die Kreislinie und der Fläche, die jeweils 2 Elemente zählen:

Numeriert man die Kreislinienpunkte mit 1 und 2, erhält man für die beiden Kreisbogenhälften die Umkehrzahlen 12-21. Deren FW 7+10 ergeben 17. Die Mitte zwischen 12 und 21 bilden die Zahlen 17 und 16.

Von diesen Zahlenzusammenhängen her ermißt sich die Bedeutung des Lebewesens Fisch.

III. PISCIS in der Doppelraute

a) Zwei Numerierungen

1. Die Doppelraute (DR) ist nach der Tetraktys die zweite eigenständige Figur im Tetraktysstern, worin sie dreimal enthalten ist. Ihre 21 Elemente sind untergliedert in 2 Rauten aus je 11 und 1 (sanduhrförmiges) Doppeldreieck aus 13 Elementen. Durch Addition ergibt sich die Summe 21+35=56.

2. Man würde nicht leicht die Fischfigur in der Doppelraute vermuten – wenn es eben nicht die Zahl 153 im Johannes Evangelium gäbe. Von der Tetraktys her gesehen stellt die Doppelraute eine Erweiterung der Fischfigur um ein Dreieck dar.

3. Durch schleifenförmige Numerierung der 7+8 = 15 Rahmenelemente gelangt man wieder zum Ausgangspunkt. Man kann entweder nur die Punkte oder Punkte und Linien numerieren. In beiden Fällen kommen 2 Positionen hinzu, 7 > 9 oder 15 > 17. Durch kreisförmige Zusammenführung der beiden Eckpunkte erhält man eine weitere Position. Zwei gefaltete DR können zur dreidimensionalen Figur des Oktaeders zusammengefügt werden:

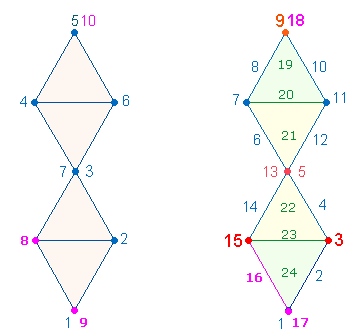
Die Numerierung der rechten Figur läßt erkennen, daß, von oben nach unten gesehen, das dritte Dreieck durch die Punkte 15 und 3 abgeschlossen wird. Die Zahlen 9 und 18 an der Spitze entsprechen den Buchstaben IS.

Wie ist nun die Verdoppelung der Buchstabenverbindung zu verstehen? Es bieten sich mehrere (sich gegenseitig ergänzende) Möglichkeiten an:

(Eine etwas spätere Bearbeitung auf der Grundlage der DR-Numerierung 1-18 bietet in knapper Form einige passende Entsprechungen zu PISCIS.)

b) Fisch mit Rückgrat

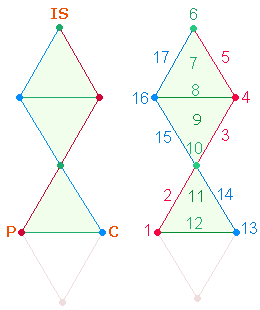
1. Die 17 Elemente der Fischfigur werden in dreifacher Bewegung durchlaufen: von P zum ersten IS hinauf, dann von dort die Mittelachse hinab und schließlich von C wieder hinauf zu IS. Um die Symmetrie des linken und rechten Aufstiegs zu gewährleisten, werden die beiden Schnittpunkte (6, 10) der Vertikalachse überlassen, sodaß die Numerierung von 1-17 in der Zahlenfolge 5-7-5 verläuft:

Die Numerierungsfolge der 5+5 sich kreuzenden Rahmenelemente und der 7 vertikalen "Rückgrat"-Elemente bewirkt, daß die beiden Zahlengruppen den Durchschnittswert 9 besitzen. Erstaunlich aber ist, daß parallel dazu auch der durchschnittliche FW jeweils 7 beträgt:

ZGr	ZS	FS	Sm.
5+5	90	70	160	112:160 = 16*(7:10)
7	63	49	112
Sm.	153	119		119:153 = 17*(7:9)

Neu bearbeitet: Juni 2007

Erstellt: April 2005

Inhalt