zurück

weiter

Anordnung der Primzahlen in 3mal 300-er Einheiten

a) Tabelle

b) Ordnung 1-900

c) Ordnung 101-1000

d) Ordnung 1-1000

ÜBERBLICK

Da in den unteren Tabellen die Primzahlen (PZ) 1-900 nach Primzahlmuster 1 geordnet werden, erscheint es sinnvoll, die PZ 1-1000 zunächst der Reihe nach darzustellen:

		Anz.	sm
0	1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97	26	1061
1	101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199	21	3167
2	211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293	16	4048
3	307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397	16	5612
4	401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499	17	7649
5	503 509 521 523 541 547 557 563 569 571 577 587 593 599	14	7760
6	601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691	16	10316
7	701 709 719 727 733 739 743 751 757 761 769 773 787 797	14	10466
8	809 811 821 823 827 829 839 853 857 859 863 877 881 883 887	15	12719
9	907 911 919 929 937 941 947 953 967 971 977 983 991 997	14	13330
	76128 = 96*13*61	169	76128

433 ist an 85. Stelle die symmetrische Mitte der 169 Primzahlen.

Die Unterteilungen der 169 Primzahlen werden weiter unten erklärt.

a) Tabelle

1. Das im vorhergehenden Kapitel vorgestellte Primzahlmuster 1 soll tabellarisch in der Anordnung von 3 mal 300-er Einheiten veranschaulicht werden. Die nicht von Primzahlen (PZ) ausgefüllten PZ-Positionen sind durch ein X gekennzeichnet. Die Abkürzung R bezeichnet der drei Reihen einer 30-er Einheit des Primzahlmusters. Innerhalb von 300 Zahlen durchläuft jede Nummer des Musters horizontal alle Ziffern von 0-9 in 30-er Folgen, vertikal enthält jede Reihe die Zahl der Primzahlpositionen je Nummer (2-4-2):

	n*30	0	1	2	3	4	5	6	7	8	9
R1		1	31	61	x	x	151	181	211	241	271
		7	37	67	97	127	157	x	x	x	277	15	1917
R2	n+1	11	41	71	101	131	x	191	x	251	281
		13	43	73	103	x	163	193	223	x	283
		17	47	x	107	137	167	197	227	257	x
		19	x	79	109	139	x	199	229	x	x	30	4102
R3	n+2	23	53	83	113	x	173	x	233	263	293
		29	59	89	x	149	179	x	239	269	x	15	2247
												60	8266

	n*30	0	1	2	3	4	5	6	7	8	9
R1		x	331	x	x	421	x	x	x	541	571
		307	337	367	397	x	457	487	x	547	577	12	5340
R2	n+1	311	x	x	401	431	461	491	521	x	x
		313	x	373	x	433	463	x	523	x	x
		317	347	x	x	x	467	x	x	557	587
		x	349	379	409	439	x	499	x	x	x	21	9071
R3	n+2	x	353	383	x	443	x	503	x	563	593
		x	359	389	419	449	479	509	x	569	599	14	6610
21021 = 21*1001 = 3*7*(7*11*13)												47	21021

Hier ist anzumerken, daß die Summe der Zahlen von 1-1000 1001*500 beträgt.

	n*30	0	1	2	3	4	5	6	7	8	9
R1		601	631	661	691	x	751	x	811	x	x
		607	x	x	x	727	757	787	x	x	877	11	7901
R2	n+1	x	641	x	701	x	761	x	821	x	881
		613	643	673	x	733	x	x	823	853	883
		617	647	677	x	x	x	797	827	857	887
		619	x	x	709	739	769	x	829	859	x	25	18859
R3	n+2	x	653	683	x	743	773	x	x	863	x
		x	659	x	719	x	x	809	839	x	x	9	6741
												45	33501
		17	19	16	14	15	16	13	14	14	14	152
33501 = 3*13*859

Jede 300-er Einheit hat 80 PZ-Positionen in der Hunderterfolge 26+28+26.

Auswertung der 4 Primzahl-Vierlinge und 5 10-er Lücken

Die 14 Primzahlen von 900-1000 sind:

907| 937 967| 991 997|| 911 919| 941 947| 971 977|| 929| 953| 983, ihre Summe 13330 bestätigt in der Quersumme 10 die Gliederung des Dezimalsystems.

b) Ordnung 1-900

1. Ordnungsstrukturen, die sich aus vorstehender Gliederung der Primzahlen erkennen lassen, sind nicht beweisbar. Sie können lediglich – mit Staunen – ermittelt und gedeutet werden. Ich beschränke mich zunächst auf das folgende Ergebnis, eines von zahlreichen möglichen:

2. Die 30*8 PZ-Positionen werden durch 19*8 = 152 Primzahlen ausgefüllt. Es ergibt sich damit das Verhältnis von 8*(11:19) ausgefallenen zu besetzten PZ-Positionen. Die Teilbarkeit durch 8 kommt erstmals nach Abschluß der ersten 300-er Einheit zustande mit dem Verhältnis 20*(1:3) von entfallenen zu besetzten PZ-Positionen:

R1	R2	R3	Sm
15	30	15	60
12	21	14	47
11	25	9	45
38	76	38	152

Die Tabelle zeigt die Häufigkeit der PZ in jeder Zehnerreihe. Entsprechend dem Verhältnis der PZ-Positionen des Grundmusters 2:4:2 ist die Zahl der ersten und dritten Reihe gleich und jeweils die Hälfte der zweiten Reihe. Dieses Ergebnis ist bereits in der ersten 300-er Einheit erreicht (15-30-15). Auf diese Weise entsteht ein Verhältnis der drei 300-er Einheiten zu einander von 1:2, da die zweite und dritte 300-er Einheit in der Addition das proportionale Verhältnis von 23-46-23 ergeben.

Die PZ-Verteilung der zweiten 300-er Einheit zeigt die Umkehrzahlen 12 und 21 für die ersten beiden 100 Hunderter als zyklisches Grundmuster der Umkehrung und die Zahl 14 für den dritten Hunderter als Faktorenwert der Summe 33. Die Endsumme 47 spiegelt auch das Verhältnis 12:21 = 4:7 wider.

c) Ordnung 101-1000

1. Die 143 dreistelligen Primzahlen teilen sich in konzentrischer Zuordnung von 100-er Einheiten in zwei Gruppen von 11*(6:7) auf. Die einzelnen 100-er Einheiten, z.B. 101-199, werden durch einstellige Ziffern gekennzeichnet:

				sm							sm	GS
1	21	2	16	37	3	16	4	17	500-549	6	39	76
9	14	8	15	29	7	14	6	16	550-599	8	38	67
	35		31	66		30		33		14	77	143
66:63 = 3*(22:21); 63:14 = 7*(9:2)

Auf die 5+4 Durchmesserelemente zweier konzentrischer Kreise übertragen, beträgt die Summe des Innendurchmessers 77, die des äußeren 66. Die 9 Zahlen sind von unten nach oben auf dem Zickzackdurchmesser der Doppelraute eingetragen:

2. Teilt man die 900 Zahlen in zwei Hälften, ergeben sich für 101-550 und 551-1000 die Umkehrwerte 76 und 67. Ordnet man den geraden Hundertern die 14 Primzahlen der 500-er Einheit hinzu, ergibt sich das Verhältnis 78:65 = 13*(6:5).

Die FW der 10 Einzelsummen ergeben ebenfalls Teilbarkeit durch 11:

PZ	21	16	16	17	6
FW	10	8	8	17	5	48
PZ	14	15	14	16	8
FW	9	8	9	8	6	40
48:40 = 8*(5:6)
88:143 = 11*(8:13)

d) Ordnung 1-1000

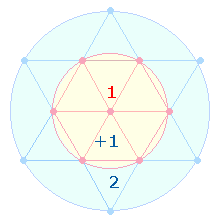
1. Die Ordnung der PZ von 1-900 zeigte sich ohne die Primzahlen 2 3 5, die aus dem Rahmen des Primzahlmusters 1 fallen. Sie haben gewissermaßen eine Libero-Funktion. Nimmt man sie hinzu, ergeben sich für 1-100 26 PZ, für 101-1000 143 PZ, ihr Verhältnis beträgt 13*(2:11). Die beiden Zahlen sind dem Grundmodell des Tetraktyssterns zuzuordnen:

Das Kreisflächenverhältnis des äußeren zum inneren Kreis beträgt (2+1):1 = 3:1.

Die Zahl 26 hat in diesem Zusammenhang besonders zwei Bedeutungen:

· Die Primzahlen 2 3 5 besetzen passend die Radialelemente der Zickzacklinie:

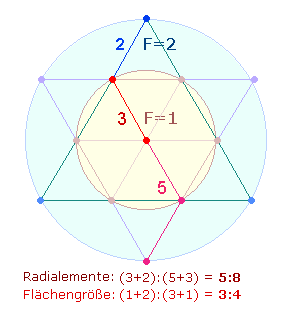
Die Radialelemente geben in analoger Weise die Flächeneinheiten des Doppelkreises wieder: 3+2 und 3+5 Radialelemente beziehen sich einmal auf den inneren Kreis und den Erweiterungsring mit 1+2 Flächeneinheiten und einmal auf den inneren Kreis und den ganzen äußeren Kreis mit 1+3 Flächeneinheiten. Auf diese Weise repräsentieren 6+7 bzw. 5+8 Radialelemente 2+5 bzw. 3+4 Flächeneinheiten. Da Radialelemente zweimal auftreten, ist die Zahl 13 auf 26 zu verdoppeln.

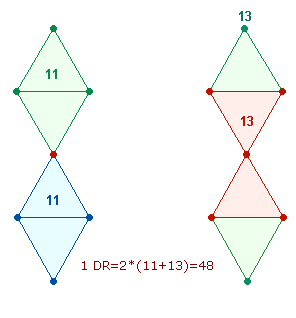
· Ein Achsenkreuz aus zwei Doppelrauten läßt sich zur dreidimensionalen Figur des Oktaeders zusammenfügen, der aus 26 Elementen (6 Ecken, 8 Flächen, 12 Kanten) besteht. Er wird durch die Kombination von zwei geometrischen Figuren aus 13 und 11 Elementen gebildet:

Das Produkt von 11*13 Primzahlen zwischen 101 und 1000 trägt dieser Kombination zweier geometrischer Figuren Rechnung.

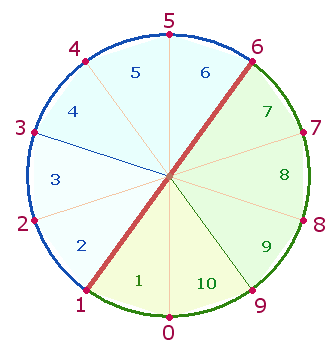
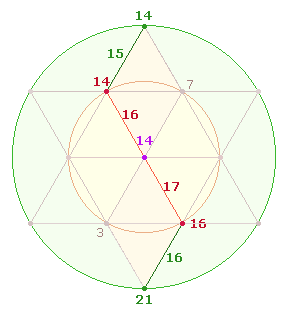
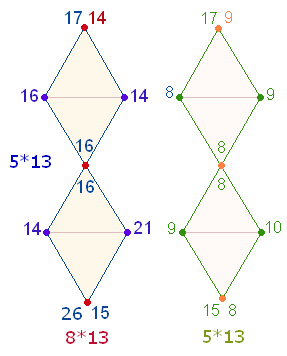
2. Bei der Oktaederbildung vereinigen sich die äußeren Punkte. Numeriert man die Punkte schleifenförmig, so daß man mit der Nr. 9 zum Ausgangspunkt 1 gelangt, ist auf der Gegenseite noch eine Position frei, die die Nr. 10 erhält. Die folgende Grafik wendet diese Numerierungsweise auf die 169 PZ der 10 Hunderter-Einheiten an:

Die Numerierung beginnt unten mit 26 und endet nach der Rückkehr zu 15 oben mit 14. Die linke Doppelraute enthält die Faktorenwerte (FW). Das Verhältnis der 4 horizontalen zu den 6 vertikalen Zahlen beträgt 13*(5:8) entsprechend den oben genannten 5+8 Radialelementen. Dasselbe Verhältnis wiederholt sich im FS:ZS-Verhältnis 13*(5:8) der vertikalen Zahlen.

Die ZS+FS der 10 Zahlen beträgt 169+101 = 270. Die ersten vier Zahlen bilden ein ZS+FS-Verhältnis mit den übrigen sechs Zahlen:

Zahl	26	21	16	16	17	14	14	16	15	14	169
FW	15	10	8	8	17	9	9	8	8	9	101
	41	31	24	24	34	23	23	24	23	23	270
	120				150
120:150 = 30*(4:5)

Die Zahlen 16 und 14 sind je dreimal vertreten. Diese 6 Zahlen haben zu den übrigen 4 Zahlen das ZS+FS-Verhältnis 141:129 = 3*(47:43).

3. Die Gesamtsumme der 169 = 13*13 Primzahlen ist 76128 = 96*13*61. Die Primzahlen der zweiten und dritten 300-er Einheit sind jeweils durch 3*13 teilbar, wie aus den betreffenden Tabellen ersichtlich ist. Ebenso durch 13 teilbar sind die Additionen der Primzahlen von 900-1000 + 1-97 sowie von 101-300: 13330+1061 = 14391 = 3*3*3*13*41; 7215 = 3*5*13*37. Die 10 100-er Einheiten lassen sich deshalb in zwei Hälften teilen: 7215+21021 = 28236 = 156*181 und 33501+14391 = 47892 = 156*307.

Der Faktor 61 erscheint auch in der FS der 4 Teilsummen (S):

S	33501	21021	7215	14391	76128
FW	875	41	58	63	1037
1037 = 17*61					77165
77165 = 5*11*23*61 = FW 100

Die Zusammengehörigkeit der Hundertereinheiten weist auf die zyklische Wirklichkeit des Dezimalsystems hin. Die Primzahlen von 1-1000 zeigen anschaulich, wie die Zahlen 9 und 10 zusammen mit der Null als Ausgangspunkt zusammenwirken, um 10 Maßeinheiten zustande zu bringen:

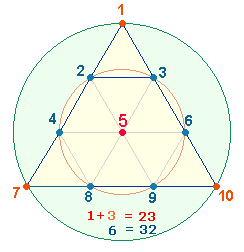
Für die Teilung der zwei Hälften in 2+3 und 3+2 gibt es zwei Modelle des Tetraktyssterns: Erstens, numeriert man die 10 Punkte der Tetraktys, ergeben die Zahlen der Eckpunkte und des Mittelpunktes 23, die der hexagonalen Kreislinienpunkte 32:

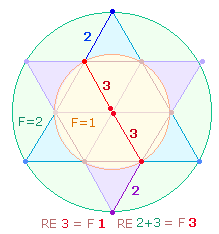
Zweitens, die 3 Radialelemente der Kreisachse werden durch die Erweiterung des Hexagons zum Hexagramm um 2 Elemente erweitert:

4. Die Einteilung der 166 Primzahlen nach ihren drei Positionsmustern berücksichtigt nicht die drei Primzahlen 2 3 5. Um Teilbarkeit durch 13 zu erreichen, stehen diese zur freien Verfügung. Das Muster 2 mit vier Positionen ergibt die Summe 37898. Durch die Hinzufügung der Primzahl 2 erhält man 37700 = 13*2900. Die Summe der zwei anderen Positionsreihen beträgt 38420, mit den PZ 3+5 38428. Das Verhältnis der beiden Summen ist 4*13*(725:739).

Erstellt: Januar 2007

Ergänzt: August 2015

Inhalt