9896 Verse der Aeneis: Trinitarische Dimension der Verszahlanordnung

9896 Verse der Aeneis: Wie Vergil sie festlegte und unterteilte

VI. Die trinitarische Dimension der Verszahlanordnung

a) Die trinitarischen Kreisflächenverhältnisse

c) Addition der Verszahlen nach dem Prinzip 1:2 und 1:3

a) Die trinitarischen Kreisflächenverhältnisse

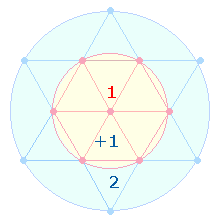
1. Geometrisches Modell des trinitarischen Gottesbildes sind die beiden Tetraktyskreise, deren Flächenverhältnis 1:3 beträgt:

Das Flächenverhältnis des hexagonalen zum erweiterten Kreisring beträgt 1:2, und die Fläche des inneren Kreises zum ganzen äußeren Kreis 1:3. Auf diese Weise erhält man 3+4 = 7 Kreisflächeneinheiten.

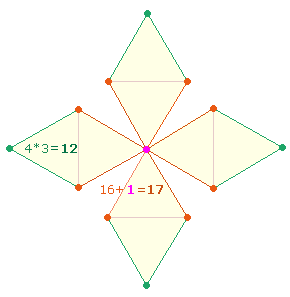
2. Die Gleichung 12 = 3*4 kann man umdrehen zu 3*4 = 12. Die 3+4 Flächeneinheiten sind nun als Faktorenwert (FW) der Zahl 12 anzusehen. Daher bestimmte Vergil für die Verszahlen der 12 Bücher zunächst die drei aufeinanderfolgenden Hundertereinheiten 7, 8, 9 und wies jeder einzelnen vier Verszahlen zu.

3. Die trinitarischen Zahlen, insbesondere 13 und 31, durchziehen die ganzen folgenden Ausführungen. Auf sie muß nicht immer hingewiesen werden.

b) Ordnung in der Unordnung

1. Nun sind die Verszahlen der 12 Bücher nicht in einer linearen Ordnung aneinandergereiht, sondern scheinbar durcheinander:

Buch	1	2	3	4	5	6	7	8	9	10	11	12	78
	756	804	718	705	871	901	817	731	818	908	915	952	9896

Am auffälligsten ist, daß die vier Verszahlen (VZ) des 900-er Bereichs linear aufsteigen und die letzten drei davon aufeinanderfolgen. Von den vier VZ des 700-er Bereichs folgen die Positionen 3 und 4 aufeinander, die vier VZ der 800-er Reihe sind durch zwei oder eine Position getrennt.

2. Wenn Vergil die Verszahlen der 12 Bücher so berechnet hat, daß die 9896 Verse mit der Faktorensumme (FS) 1523 eine Einheit bilden, dürfte er auch die 12 Positionen der VZ selbst in diesem Sinne gestaltet haben. Man wird also die zusammenhängenden und nicht zusammenhängenden Positionen als zwei Gruppen von 5 und 7 VZ ansehen:

				sm					sm	GS	FW
Pos.	3	4	-	7	10	11	12	-	33	40	11
FW	3	4	-	7	7	11	7	-	25	32	10
	6	8	-	14	17	22	19	-	58	72	21
Pos.	6	1	8	15	2	5	7	9	23	38	21
FW	5	1	6	12	2	5	7	6	20	32	10
	11	2	12	27	4	10	14	15	43	70	31
GS				41					101	142	52

Auf die zahlreichen Ergebnisse beider Tabellen ist in den folgenden Punkten näher einzugehen:

· Die ZS 40+38 sind Konstitutive ihrer Summe 78, ebenso die ZS+FS 72+70. Letztere ermöglichen einen Blick auf die objektive Bedeutung der Summe 142:

72	70	142
12	14	26
84	84	168

Die Summe 142 verbindet die Zahlen 12 und 10. Für die Zahl 12 ist 142 die ZS 78 + die FS 64, für die Zahl 10 die 4Werte:

	ZS	FS
	55	46	101
FW	16	25	41
	71	71	142

Die Entfaltung des Kreises zum Tetraktysstern ist auf die Bildung des Oktaeders ausgerichtet. Dieser besteht aus 12 Kanten und 6 Ecken + 8 Flächen = 14 Elemente. 12 und 14 sind die FW von 72 und 70, nicht nur ihre Multiplikation ergibt 168, sondern auch die gleichen Summen 84.

· Die eigentliche Bedeutung der ersten Tabelle besteht in ihrer trinitarischen Dimension. Sie wird auf folgende Weise erkennbar:

Den Kreisflächeneinheiten 1+2 und 1+3 entsprechen komplementär die Zahlen 9+8 = 17 und 9+7 = 16 auf der Skala der Grundzahlen 1-9. Deren FS wiederholen in zweistelliger Zusammensetzung die Kreisflächeneinheiten: 6+6 = 12; 6+7 = 13. 17+12 und 16+13 ergeben dieselbe ZS+FS 29. Die FW der Kreislächeneinheiten sind mit diesen identisch. Somit ergibt sich tabellarisch das folgende Bild:

		ZS			FS	GS			ZS			FS	GS	GZS	GFS	GZFS
1	2	3	1	2	3	6	1	3	4	1	3	4	8	7	7	14
9	8	17	6	6	12	29	9	7	16	6	7	13	29	33	25	58
10	10	20	7	8	15	35			20			17	37	40	32	72

Nun stellt sich heraus, daß nicht nur die Summe der vier Komplementärzahlen und der Bücher 10+11+12 jeweils 33 ist, sondern auch deren FS jeweils 25:

10	11	12	33
7	11	7	25
17	22	19	58

Das vornehmste gematrische Beispiel der komplementären trinitarischen Dimension ist der Name MARIA:

	M	A	R	I	A	sm
ZW	12	1	17	9	1	40
FW	7	1	17	6	1	32
						72

Die Buchstaben MR enthalten die FW 6+6 und die Zahlen 9+8. Das geometrische Modell der Zahlen 12 und 17 sind die 29 Rahmenelemente des DR-Kreuzes:

Die 12 Erweiterungselemente und 17 hexagonalen Elemente repräsentieren das Kreisflächenverhältnis 2:1.

· Die zwei Gruppen von 5 und 7 Verszahlpositionen erscheinen nur von begrenztem Wert, wenn nicht die zwei Summen der Verszahlen selbst genau bedacht wären:

										GS	FW
VZ	718	705	-	1423	908	915	952	-	2765	4198	2101
FW	361	55	-	416	231	69	30		330	746	375
sm				1839						4944	2476
VZ	901	756	731	2388	804	871	817	818	3310	5698	57
FW	70	20	60	150	74	80	62	411	627	777	47
sm				2538						6475	104
GS										11419	2580

Die Ergebnisse sind schwierig zu interpretieren, weil man wissen müßte, worauf es Vergil besonders ankam und welche höchstes Aussageziel er anstrebte. Bei den vielen möglichen Rechenergebnisse ist schwer zu entscheiden welche Vergil wirklich intendierte. Zunächst ist festzustellen, daß die ZS 4198 und 5698 jeweils auf -98 enden, daß also der Abstand zwischen beiden Zahlen 1500 = 30*50 beträgt.

Die FS 746 = 2*373 und 777 = 21*37 sind beide auf die Tetraktys beziehbar. Die Einzelziffern der ersten FS gibt 7 hexagonale und 4+6 Tetraktyspunkte in der Bedeutung von 1+3+1 Flächeneinheiten. Die Einzelziffern der FS 777 weisen auf die 3*7 Elemente der drei Tetraktysseiten hin. Die ZW/FW-Verrechnung ergibt folgendes:

			sm	FW	sm	FW
FS	746	777	1523	1523
FW	375	47	422	213
sm			1945	1736	3681	415
FW			494	44	438	78
sm	493 = 17*29					493
1736 = 5631 >FW 13+31 = 44; 438 = 673

Die Faktoren des Endergebnisse 17*29 ist, wie oben bereits dargelegt auf die 29 Rahmenelemente des DR-Kreuzes zu beziehen, 17 davon gehören dem hexagonalen Bereich an. 17+29 Elementen geben daher das Kreisflächenverhältnis 1:3 wieder. Trinitarisch ist auch die Zusammensetzung des FW 13+31 = 44.

Vergil wird auch die ZV-Positionen mitbedacht haben:

	Gr.1		sm	Gr.2		sm	GS
	VZ	Pos.		VZ	Pos.
ZS	4198	40	4238	5698	38	5736	9974
FS	746	32	778	777	32	809	1587
			5016			6545	11561
5016:6545 = 11(456:595); 456 = 2419; 595 = 35*17

Beide Teilsummen sind durch 11 teilbar. Ihre Differenz beträgt 11*139. Aus 13+9 Elementen bestehen das hexagonale Achsenkreuz und das rechtwinklige Achsenkreuz. Sie enthalten die für das Dezimalsystem relevanten 6+4 = 10 Maßeinheiten.

Von den ZS und FS obiger Tabelle lassen sich die FW ermitteln:

	Gr.1		sm	Gr.2		sm	GS
	VZ	Pos.		VZ	Pos.
FW	2101	11	2112	57	21	78	2190
FW	375	10	385	47	10	57	442
	2476	21	2497	104	31	135	2632
2632 = 2*1316 = 2(2847) = FW 2*58

Die Zahlen 13 und 16 setzen sich, wie oben dargestellt, aus den FW 6+7 und den Zahlen 9+7 zusammen. Sie sind die Entsprechung zu 1+3 Kreisflächeneinheiten. Die 29 Rahmenelemente des DR-Kreuzes bestehen aus 13 Punkten und 16 Linien:

Als DR-Kreuz stellt sich auch der Ausdruck 2*(28*47) dar. Denn eine Doppelraute besteht aus 2+8 Linien, 4 Flächen und 7 Punkten. Der FW 58 weist auf die beiden komplementären Kreisflächenverhältnisse, die oben behandelt wurden. Sie werden auch sichtbar in der Addition der Aufteilung 26+32 = 58. Man darf annehmen, daß Vergil die Summe 2632 angestrebt hat, umso mehr, als die Verrechnung der 4Werte ein beeindruckendes Ergebnis erbringt:

	ZS	FS	FW1	FW2	sm	FW
	9974	1587	2190	442	14193	108
FW	4989	49	83	32	5153	5153
sm						5261
FW	14193 = 19747 = 919*83

Die ZS+FS 11419 wird durch Hinzunahme der Positionen 1-12 und den FW1/2-Summen um 2*73 von 601*19 auf 747*19 erhöht. Die Primzahl 5261 entspricht in zweiteiliger Aufteilung den ZS 113 der Wörter OPERA TENET des SATOR-Quadrats, das als wichtigster Bezugspunkt aller gematrischen Bemühungen anzusehen ist.

4. Nach den zwei Gruppen von VZ sollen nun die dreimal vier Buchpositionen untersucht werden:

	700				sm	800				sm	900				sm	GS
Buch	1	3	4	8	16	2	5	7	9	23	6	10	11	12	39	78
FW	1	3	4	6	14	2	5	7	6	20	5	7	11	7	30	64
					30					43					69	142

Der FW von 39 = 3*13, der Hälfte der Gesamtsumme 78, ist 16, die Positionssumme (PS) der 700-er Reihe. Die PS 23 der 800-er VZ stellt die Differenz zwischen dem FW 16 und der Zahl 39 dar.

Von den ZS und FS sind nun noch deren FW zu ermitteln:

				sm				sm	GS	FW	GS2
ZS	16	23	39	78	8	23	16	47	125	15	140
FS	14	20	30	64	9	9	10	28	92	27	119
	30	43	69	142	17	32	26	75	217	42	259
217 = 7*31

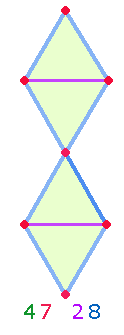
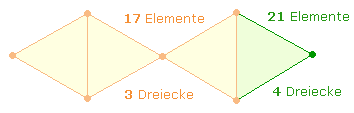
Die Einzelziffern der FW1-Summe 47 und der FW2-Summe 28 entsprechen den 4 strukturellen Elementen der Doppelraute (DR) und lassen sich als Gleichung 4*7 = 28 verstehen:

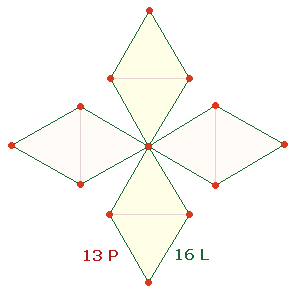
Die besondere Bedeutung der Zahl 217 liegt in ihrer zweistelligen Aufteilung 21 und 17: Die 21 Elemente der DR enthalten 4 Dreiecksflächen, die 17 Elemente der "Fischfigur" 3 Dreiecksflächen:

Die Faktoren 7*31 entsprechen also den beiden geometrischen Figuren: Durch die Aufteilung der Elemente in 17+4 und 17+21 ergeben sich die Flächenverhältnisse 3:1 und 3:4.

Die FW der Summen 142 und 75 sind 73+13 = 86. Zusammen ergibt sich 303, die ZS des SATOR-Quadrats.

5. Die Positionsfolgen der drei Hunderterreihen haben jeweils eine eigene Bedeutung:

	700					800					900
Buch	1	3	4	8	16	2	5	7	9	23	6	10	11	12	39

Der ersten Folge entsprechen zwei Gleichungen: 1+3 = 4 und 1+3+4 = 8. Mit der ersten Gleichung werden die zweimal 4 Punkte der DR charakterisiert. Die Zahl 1 steht dabei für einen zweiten Mittelpunkt. Die zweite Gleichung verdoppelt die DR zu einem DR-Kreuz.

In der zweiten Gleichung geht es um eine Teilung, um die Elemente der Kreisteilung:

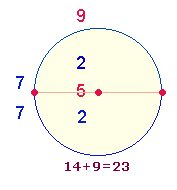
Der ungeteilte Kreis besteht aus 3 Elementen, Mittelpunkt, Kreisbogen und Fläche. Durch Einziehen eines Durchmessers erhöht sich die Zahl der Elemente auf 9. Der Durchmesser (DM) selbst besteht aus 5 Elementen. Will man also eine einzelne Kreishälfte definieren, kommen zu den 5 DM-Elementen noch ein halber Kreisbogen und eine halbe Fläche hinzu. Es entsteht so der Doppelaspekt von zwei Hälften und dem Ganzen.

Die dritte Positionsfolge stellt das 1:3 Verhältnis von zweimal drei konzentrischen Zahlenpaaren dar. Die Zahl 6 besteht demnach aus 1+2+3. Konzentrisch angeordnet, ergeben sich folgende ZS und FS für die drei Zahlenpaare:

			sm			sm				GS
Zahl	1	12	13	2	11	13	3	10	13	39
FW	1	7	8	2	11	13	3	7	10	31
			21			26			23	70
21:49 = 7(3:7) = 710

Die Faktoren 7*10 verweisen auf die 7 hexagonalen Punkte und ihre Erweiterung auf 10 Tetraktyspunkte, sie geben das Kreisflächenverhältnis 1:3 wieder.

Erstellt: November 2016

Letzte Änderung: Mai 2018

domum

index