Die gematrischen Werte von

SENATUS POPULUSQUE ROMANUS

TEIL 1

I. Allgemeine gematrische und trinitarische Aspekte

II. POPULUSQUE

a) POPULUS + QUE

b) Faktorenwerte

c) Zwei Teilungen

d) Die Palindrome POP-ULU

e) 10 Punktepositionen der DR

TEIL 2

III. 3, 2 u. 4 Teile

IV. 24 Buchstaben in der DR

V. 8x3 Buchstaben

VI. SENATUS POPULUSQUE ROMANUS + SPQR

I. Allgemeine gematrische und trinitarische Aspekte

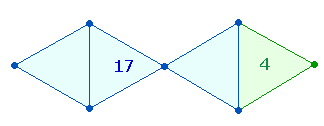
1. Das trinitarische Prinzip 1 und 3 ist gematrisch nicht nur in RO+MA = 31+13 verwirklicht, sondern in sehr ähnlicher Weise im römischen Hoheitstitel SENATUS POPULUSQUE ROMANUS. Zur jeweiligen Zahlensumme (ZS) und Faktorensumme (FS) kommen noch deren FW1/2 hinzu:

	ZS	FS	sm	FW1	FW2	sm	GS
SENATUS	94	63	157	49	13	62	219
POPULUSQUE	154	84	238	20	14	34	272
ROMANUS	95	64	159	24	12	36	195
sm	343	211	554	93	39	132	686
343 = 7*7*7; 686 = 2*343

Die relevantesten Ergebnisse der Tabelle werden im Folgenden ausgewertet.

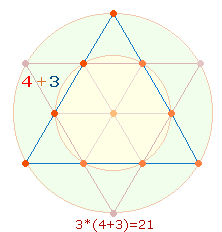
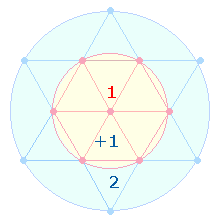
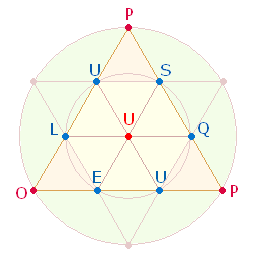
2. Relevantester Bezugspunkt der ZS 343 ist die Tetraktys, deren Seiten aus 3mal 4 Punkten + 3 Linien besteht:

Die 4Werte ergeben, in 1:3 aufgeteilt, zweimal dieselbe Summe 343. Die übrigen 3 Werte fügen also der ersten Tetraktys noch die zweite hinzu.

In der 4. Ekloge, in der VERGIL mehrere Textkreise angelegt hat, beträgt die 4W-Summe der vier Mittelpunkte ebenfalls 686. Beide Wortgruppen sind aufeinander abgestimmt. Vergil verbindet damit den Wunsch, daß Rom auch unter der zukünftigen Friedensherrschaft Mittelpunkt sei. Man kann also davon ausgehen, daß jeder gebildete Römer die gematrischen Eigenschaften seines staatlichen Hoheitszeichens kannte.

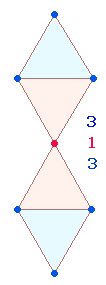
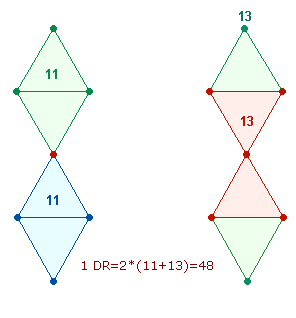
3. Die Summen der FW1/2 und Umkehrzahlen 93 = 3*31 und 39 = 3*13 sind auf zwei Doppelrauten (DR) mit der trinitarischen Punktestruktur 3-1-3 zu beziehen und verweisen auf das Endziel der Oktaederbildung aus einem DR-Kreuz:

4. Die ZS und FS der drei Wörter zeigen zwei häufige gematrische Prinzipien. Die ZS von SENATUS (94) und ROMANUS (95), aus je 7 Buchstaben bestehend, sind angrenzende Konstitutivzahlen ihrer Summe 189 = 27*7. In der Addition durch 7 teilbar, erweisen sich beide Wörter konzentrisch auf das Mittelwort POPULUSQUE ausgerichtet, dessen ZS 154 = 22*7 allein durch 7 teilbar ist. Der Differenzbetrag zwischen FS und ZS ist beide Male 31. 31 ergibt sich auch aus der ZW/FW-Verrechnung:

			sm	FW
ZS	189	154	343	21
FW	16	20	36	10
sm				31

Zahlenverhältnisse zwischen FS und ZS der Randwörter bestehen nicht, da sie schon durch die Nachbarschaft ihrer ZS gekennzeichnet sind.

Proportionale Beziehung zwischen FS und ZS hingegen übernimmt POPULUSQUE: 84:154 = 14*(6:11). Die ZS+FS 238 = 14*17 ist die FS 6*17 + ZS 8*17 der Zahlen 1-16. Den Produktzahlen 17 und 14 entspricht die Silbe RO in ROMA.

5. Ein Oktaeder besteht aus 12 Kanten sowie 6 Ecken + 8 Flächen, in zweifach zusammengefaßter Summe aus 12+14 Elementen. Ein Bezug zu diesen zwei Zahlen zeigt sich in den drei Wörtern SENATUS POPULUSQUE ROMANUS auf folgende Weise:

Die drei Wörter bestehen aus 7+10+7 Buchstaben. Liest man die Zahl 10 zweimal, ist eine Umkehrbewegung von 7 Hexagonpunkten zu 10 Tetraktyspunkten und von dort zurück wieder zum Hexagon zu erkennen. Die Palindromform der drei Buchstabenzahlen begründet eine konzentrische Struktur, die von außen nach innen ablaufen kann und in der Mitte von 12+12 Buchstaben endet. Die Gleichheit von je 12 Buchstaben erhält man jedoch auch durch die konzentrische Gliederung 6+12+6. Das ZS-Verhältnis der 12+12 Buchstaben ist 154:189 = 7*(22:27). Dieses Verhältnis kehrt sich um zu 7*(27:22) beim nächsten konzentrischen Schritt 14+10.

6. Das Prinzip der Gleichheit zweier Hälften ist auch darin verwirklicht, daß die ZS+FS 554 in der Mitte der 24 Buchstaben in 277+277 geteilt wird:

	ZS	FS	sm	FW1	FW2	sm	GS
SENATUS POPUL-	169	108	277	26	13	39	316
USQUE ROMANUS	174	103	277	34	103	137	414
	343	211	554	60	116	176	730
26:13 = 13*(2:1); 60:116 = 4*(15:29)

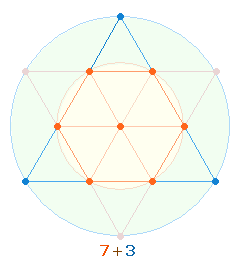
– Die Summe der 4Werte 730 enthält in der Lesart (7+3)+10 wiederum die Verdoppelung der Tetraktys.

– Das trinitarische Prinzip 1 und 3 tritt in Erscheinung durch die Zahlen 169 (13²), 39 (3*13) und 103. In diesem Sinne bilden die ZS und ihre FW ein Zahlenverhältnis:

ZS	FW	sm
169	26	195
174	34	208
343	60	403
195:208 = 13*(15:16)
403 = 13*31

– Die Primzahl 277, aufgeteilt in 27+7, bezieht sich auf die Punkte und Flächen des Tetraktyssterns und seiner beiden Kreise: Die Zahl 27 setzt sich zusammen aus (7+6)+(7+7) Punkten und repräsentiert die Flächengrößen (1+2)+(1+3), indem der Mittelpunkt des hexagonalen Kreises, der für den Erweiterungskreises (6+1) ein zweites Mal benutzt wird, für dessen gesamte Flächengröße 3 steht.

– Die FW 26 und 34 beziehen sich auf die Elemente des ganzen Oktaeders und zweier Hälften.

– Eine Überlegung wert ist das Wort USQUE – immerfort, ohne Ende, das durch die Teilung der 24 Buchstaben in Erscheinung tritt. Römischem Staat und Gesellschaft wird damit immerwährende Dauer zugesprochen.

7. Die 12+12 Buchstaben sollen noch differenzierter betrachtet werden:

SENATUS POPUL | USQUE ROMANUS

Die Buchstaben SNA stehen in spiegelbildlicher Position, ihre ZS+FS ist 32+22 = 54.

8 Buchstaben sind in jeder Hälfte gleich:

	ZS	FS	sm	FW
AEOUU	60	33	93	34
NSS	49	29	78	18
	109	62	171	52
93:78 = 3*(31:26); 52=4*13

Das ZS+FS-Verhältnis der drei konzentrischen Buchstaben zu den übrigen fünf ist 54:117 = 9*(6:13).

Ohne Verdoppelung ist das Zahlenverhältnis der Vokale zu den Konsonanten 4:2, mit Verdoppelung 5:3. Ersteres Verhältnis ist auf 4:2 Maßeinheiten der beiden Tetraktyskreise und ihrer Durchmesserelemente beziehbar, letzteres auf die Radialelemente.

Vier Buchstaben auf jeder Seite sind verschieden:

	ZS	FS	sm
TPPL	60	46	106
QURM	65	41	106
	125	87	212

8. Zu gematrischer Vollkommenheit gehören auch sinnvolle Beziehungen zwischen Vokalen und Konsonanten. Dies ist hier der Fall:

a(2) e(2) o(2) u(5)	11 V	140
l (1) m(1) n(2) p(2) q(1) r(1) s(4) t(1)	13 K	203
140:203 = 7*(20:29)

Die Buchstabenzahlen 11 und 13 entsprechen den beiden geometrischen Figuren, aus denen der Oktaeder besteht:

9. Von den 21 Buchstaben des lateinischen Alphabets sind 12 in SENATUS POPULUSQUE ROMANUS enthalten:

	A	E	L	M	N	O	P	Q	R	S	T	V	sm
ZW	1	5	11	12	13	14	15	16	17	18	19	20	161
FW	1	5	11	7	13	9	8	8	17	8	19	9	115
	12		5*31 = 155; 109+155 = 264 = 22*12										276
115:161 = 23*(5:7)

10 Buchstaben L-V bilden eine durchgehende Folge. Das ZS+FS-Verhältnis zu den übrigen 11 Buchstaben beträgt 264:132 = 132*(2:1).

Das FS:ZS-Verhältnis 5:7 entspricht dem der Zahlen 1-21: 165:231 = 33*(5:7) = 33*12. Die ZS+FS 276 ist die Summe der Zahlen 1-23. In der Aufteilung 4*69 gibt sie die ZS der vier Seiten des SATOR-Quadrats wieder. Die restlichen 9 Buchstaben haben somit das FS:ZS-Verhältnis 50:70 = 10*(5:7):

	B	C	D	F	G	H	I	K	X	sm
ZW	2	3	4	6	7	8	9	10	21	70
FW	2	3	4	5	7	6	6	7	10	50
30+27 = 57							40+23=63			120
57:63 = 3*(19:21)

Jeweils 3 Buchstaben der ersten beiden Gruppen sind zusammenhängend und ergänzen sich konzentrisch zu 10.

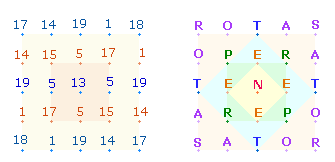
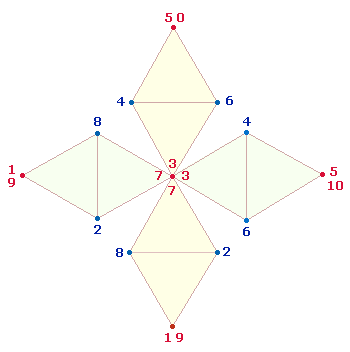
Die Teileraufteilung 23:10 hat eine Entsprechung im Achsenkreuz des inneren SQ:

Die Buchstaben ENE haben die ZS 23, die zwei anderen E die ZS 10. Das ZS-Verhältnis der 5 Buchstaben zu den umgebenden 5+5 Buchstaben der drei Mittelzeilen beträgt 33*(1:2:2) = 165, was der FS der Zahlen 1-21 entspricht.

Die 12+9 Buchstaben lassen sich auf die drei Tetraktysseiten anordnen:

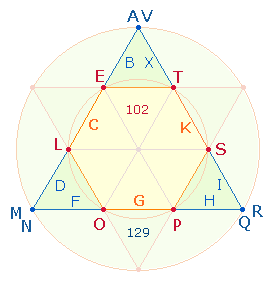
Die 3:6 Linien-Buchstaben haben die ZS 20 und 50. Die Buchstaben CGK repräsentieren für sich allein die 20 Punkte von 2 Tetraktys. Die 9 hexagonalen Buchstaben haben die gleiche ZS 102 wie die 8 verschiedenen Buchstaben des SQ. Das Verhältnis der beiden Summen 102:129 ist 3*(34:43). Das FS-Verhältnis der 9 hexagonalen Buchstaben zu den 12 Buchstaben der Erweiterung ist 77:88 = 11*(7:8).

10. Die gleichen Hälften 12+12 haben zwei Bezugspunkte:

– 12 Linien des Hexagons sowie des Erweiterungsbereiches;

– 12 Dachelemente je Doppelraute; bei der Oktaederbildung aus einem DR-Kreuz konvergieren die 24 Elemente zu 12.

Nach einem Numerierungsmodell können die 24 Buchstaben auf einer Doppelraute angeordnet werden, wie weiter unten ausgeführt wird.

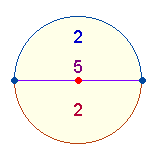
11. Die Einzelziffern der FS 211 (Primzahl) geben die Flächenverhältnisse der beiden konzentrischen Kreise des Tetraktyssterns wieder:

II. POPULUSQUE

a) POPULUS + QUE

1. POPULUS besteht wie die beiden anderen Wörter aus 7 Buchstaben und könnte mit ihnen die drei Tetraktysseiten aus je 4 Punkten + 3 Linien besetzen. Das angehängte –QUE assoziiert POPULUS jedoch mit den 7 Hexagonpunkten, die durch –QUE um drei weitere Punkte zu 10 Tetraktyspunkte erweitert werden:

2. Die ZS+FS beider Wortbestandteile sind durch 7 teilbar:

	ZS	FS	sm
POPULUS-	113	62	175
QUE	41	22	63
	154	84	238
175:63 = 7*(25:9)

Der FW von 175 = 7*25 beträgt 7+10 = 17 und gibt entweder die 7 Punkte des Hexagon und 10 Punkte der Tetraktys wieder oder 7 Punkte und 10 Linien der DR. Die Zahl 63 = 3*21 ist auf drei DR beziehbar.

Die Quadratzahlen 25:9 stellen ein 5*5 Punkte-Quadrat dar, worin sich konzentrisch ein 3*3 Punkte-Quadrat befindet.

Die FS 84 kann man verstehen als Zusammensetzung der ZS 45 + FS 39 der Grundzahlen 1-9 dar. Das FS:ZS-Verhältnis Verhältnis ist 3*(13:15).

b) Faktorenwerte

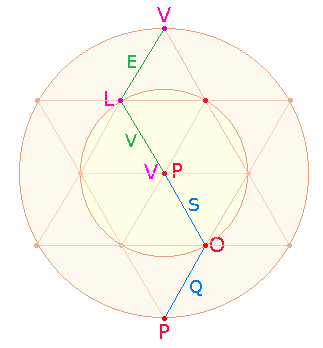
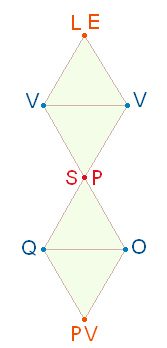
1. Die Differenz zwischen der FS 84 und der ZS 154 beträgt 70, wodurch sich ein theoretischer Differenzdurchschnitt 7 je Buchstabe ergibt. Die ungewöhnlich hohe Differenz liegt daran, daß L und E die einzigen Primzahlbuchstaben in POPULUSQUE sind. Sie stehen an 5. und 10. Stelle und finden bei schleifenförmiger Besetzung der Rahmenlinien der DR einen (fast) natürlichen Platz auf den Querlinien:

Das ZS-Verhältnis der 5+5 Buchstaben in den beiden Rauten beträgt 70:84 = 14*(5:6).

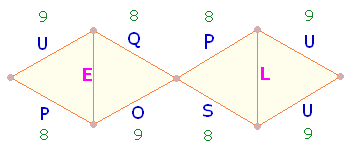
2. Alle 8 Buchstaben des DR-Rahmens haben im regelmäßigen Wechsel den FW 8 und 9 bzw. 9 und 8. Die FS der Buchstaben LE ist 11+5 = 16. Das FS-Verhältnis der 8:2 Buchstaben ist 68:16 = 4*(17:4). Dieses Verhältnis hat zwei wesentliche Bedeutungen:

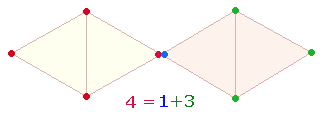
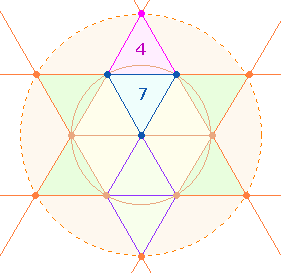
– Die erste Bedeutung hat einen trinitarischen Bezug: In der Tetraktys sind drei geometrische Figuren erkennbar, die drei Dreiecksflächen enthalten:

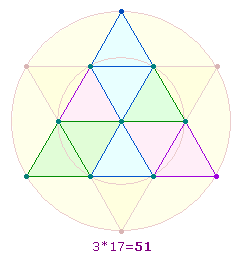
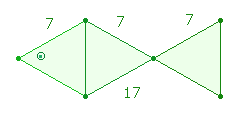
Jede besteht aus 17 Elementen. Das sind 4 Elemente weniger, als drei getrennte Dreiecke aus je 7 Elementen zählen würden. Diese 4 Elemente bilden in der DR das vierte Dreieck:

Die "Fischfigur" kann von jedem der beiden Eckpunkte gebildet werden. Im DR-Kreuz sind es dann 4, was dem gemeinsamen Multiplikator des Verhältnisses 4*(17:4) entspricht.

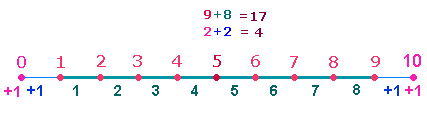
– Die zweite Bedeutung geht von 9 Grundzahlen aus, die als Punkte 8 Maßeinheiten begrenzen: Um auf einer Strecke 8+2 = 10 Maßeinheiten zu erhalten, sind zwei weitere Punkte erforderlich:

c) Zwei Teilungen

1. Die ZS+FS der beiden Hälften von POPULUSQUE sind:

	ZS	FS	sm	FW1	FW2	sm	GS
POPUL-	75	45	120	13	11	24	144
USQUE	79	39	118	79	16	95	213
	154	84	238	92	27	119	357
119:238 = 119*(1:2); 357 = 21*17

Die Summe der FW1/2 beträgt die Hälfte der ZS+FS 238. Das Produkt 21*17 ist auf den Doppelaspekt von 17 und 21 Elementen der "Fischfigur" beziehbar:

Die Einzelziffern der Zahl 357 bilden drei Mittelpunkte der Zahlen 1-9, die dreimal 5 Punkte + 4 Linien umfassen. Dies ist auch bei den dreimal 9 Durchmesserelementen der Doppelraute der Fall. In der Lesung 3*(5:7) bedeuten die Einzelziffern die Elemente von drei Hexagonachsen und drei Tetraktysseiten. Eine trinitarische Gemeinsamkeit von 21 und 17 ist auch darin zu sehen, daß jede Tetraktysseite aus drei Linien und eine (von dreien, vom Tetraktysrahmen umschlossene) Fischfigur aus drei Dreiecken besteht.

2. Die FW1/2 sowohl des ganzen als auch des geteilten POPULUSQUE sind durch 17 teilbar: 34:119 = 17*(2:7). Das Verhältnis 7:2 bezeichnet die Zahl der Kreiselemente, wenn man durch den Kreismittelpunkt eine Achse zieht und man deren 5 Elemente zu einem halben Kreisbogen und einer halben Kreisfläche hinzuzieht:

Mit der ZS+FS 238 ergeben die FW1/2 zusammen 272:357 = 17*(16:21) = 17*37.

Aus dem Wort POPULUSQUE allein ist also erkennbar, daß es in der römischen Gesellschaft einerseits zwei unterschiedene Klassen gibt, diese aber zusammen eine komplementäre Einheit bilden.

3. Auch nach dem 4. Buchstaben zeigt sich ein bedeutendes Zahlenverhältnis:

	ZS	FS	sm	FW1	FW2	sm	GS
POPU-	64	34	98	12	19	31	129
LUSQUE	90	50	140	13	12	25	165
	154	84	238	25	31	56	294
98:140 = 14*(7:10); 56:238 = 14*(4:17)

Die vier Buchstaben können auf die drei Eckpunkte der Tetraktys und den Mittelpunkt, die übrigen 6 Buchstaben auf die Kreislinienpunkte des inneren Kreises plaziert werden:

Dem ZS+FS-Verhältnis 7:10 entsprechen – in gegenseitigem Verweis – die Punktezahlen des Hexagon und der Tetraktys. Die 4 Buchstaben vertreten 3 Flächeneinheiten des äußeren Kreises, die übrigen 6 Buchstaben 1 Flächeneneinheit des inneren Kreises.

Die ZS+FS der 3 Eckpunkte und der 7 Hexagonpunkte sind 69 = 3*23 und 169 = 13², ihre FW sind jeweils 26.

d) Die Palindrome POP-ULU

1. Auffällig ist das doppelte Palindrom POPULU-SQUE. Die zweimal 3 Buchstaben und die übrigen vier lassen an zweimal 5 Durchmesserelemente des Tetraktyssterns denken:

Die gematrische Überprüfung weist die 6 Buchstaben nicht den hexagonalen Radialelementen, sondern den 5 DM-Punkten zu. Die beiden restlichen Buchstabenpaare SQ-UE werden in natürlicher Reihenfolge von innen nach außen zuerst POP und dann ULU zugeordnet.

2. Die ZS+FS jeder so angeordneten Buchstabenhälfte ist nicht nur gleich, sondern die ZS und die FS sind jeweils die benachbarten Konstitutivzahlen ihrer Summen: 78+76 = 154, 41+43 = 84:

SQ	P	O	P	S	Q	sm	U	L	U	U	E	sm
ZW	15	14	15	18	16	78	20	11	20	20	5	76
FW	8	9	8	8	8	41	9	11	9	9	5	43
	23	23	23	26	24	119	29	22	29	29	10	119

Die ZS und FS der 6 Buchstaben der hexagonalen Radialelemente und der 4 Buchstaben des Erweiterungsbereiches bilden jeweils ein Zahlenverhältnis:

SQ	P	O	S	U	L	U	sm	Q	P	E	U	sm
ZW	15	14	18	20	11	20	98	16	15	5	20	56
FW	8	9	8	9	11	9	54	8	8	5	9	30
98:56 = 14*(7:4); 54:30 = 6*(9:5)

Die gemeinsamen Teiler 14+6 = 2*(7+3) lassen sich auf jeweils 10 Punkte von zwei Tetraktys beziehen.

3. Es besteht zweimal Parallelität von PU und einmal von OL:

SQ	P	U	sm	O	L	sm
ZW	15	20	35	14	11	25
FW	8	9	17	9	11	20
	23	29	52	23	22	45
15:20 = 5*(3:4) = 5*7
35:25 = 5*(7:5)
20:25 = 5*(4:5)

Die Einzelziffern der Zahl 35 und die Produktzahlen 5*7 haben als Gemeinsamkeit, daß sich die erste Zahl auf den hexagonalen Kreis, die zweite auf den ganzen äußeren Kreis bezieht. 3 und 5 betreffen die Radialelemente, 5 und 7 die Punkte der Doppelraute (DR). Beide Zahlenpaare geben das Kreisflächenverhältnis 1:3 wieder. Auch das ZS-Verhältnis 5*(7:5) ist in diesem Sinne zu verstehen.

Die Verdoppelung der Parallelität ist auf zwei DR zu beziehen, die in Form eines Achsenkreuzes zu einem Oktaeder zusammengefügt werden können. Dies gilt auch für die Einzelziffern des Produkts 4*13 der ZS+FS 52, die als Punkte zweier Rauten zu verstehen sind:

Das Verhältnis 20:25 = 5*(4:5) hat eine doppelte Bedeutung: Erstens, 5:9 Durchmesserelemente repräsentieren ebenfalls das Flächenverhältnis 1:3. Zweitens, das interne Verhältnis 5*(4:1) ist als 5+5 Radialelemente interpretierbar.

4. Die Buchstaben OL besetzen hexagonale Kreislinienpunkte. Sie stehen in der Mitte zweier spiegelsymmetrischer Dreiecke, die eine Raute bilden:

Wie die Grafik zeigt, besteht ein Dreieck aus 7 Elementen. Bei der Erweiterung zum Tetraktysstern kommen noch 4 Elemente hinzu. Eine Raute besteht also aus 11 Elementen, zwei Dreiecke jedoch aus 14 Elementen. Die Buchstabenentsprechungen der beiden Summen sind LO. Genau diesen Zusammenhang gibt das oben ermittelte ZS-Verhältnis 14*(7:4) des hexagonalen und des Erweiterungsbreichs wieder.

e) 10 Punktepositionen der DR

1. Die Doppelraute (DR) ist die eckige Schwester der Ziffer 8, die man kreisförmig umfahren kann. Numeriert man auf diese Weise die Punkte der DR, bis man den Anfang erreicht, erhält man 9 Positionen. Nun ist das Ziel des Tetraktyssterns die Erreichung einer dreidimensionalen Figur, des Oktaeders. Durch die Vereinigung der Endpunkte kommt eine weitere Numerierungsposition hinzu. Besetzt man die 10 Positionen einmal von 1-0 und einmal von 1-10, ergibt sich ein gleiches FS:ZS-Verhältnis 17:20 der zweimal 6 vertikalen und 4 horizontalen Zahlen, 3*(17:20) und 2*(17:20):

Der Buchstabe Q bezeichnet durch den Schrägstrich das Überschreiten der 9. zur 10. Position. Sein ZW 16 geht aus den nunmehr 6 (statt 7) Punkten + den 10 Linien hervor, der ZW 20 des begleitende V aus den nunmehr 20 Elementen der DR. Wenn nun die Verbindungspartikel –QUE in der Kurzformel SPQR eine eigene Initiale bildet, könnte auch die Besetzung der 10 Buchstaben von POPULUSQUE nach dem besprochenen Numerierungsmodus eine bedeutende Rolle spielen:

Die ZS+FS der horizontalen und vertikalen Buchstaben sind:

	ZS	FS	sm
QO-VV	70	35	105
PV-SP-LE	84	49	133
	154	84	238
70:84 = 14*(5:6); 35:49 = 7*(5:7)
49:84 = 7*(7:12)

Alle vier Werte sind durch 7 teilbar und bilden entsprechende Verhältnisse. Diese sind im Folgenden näher zu betrachten.

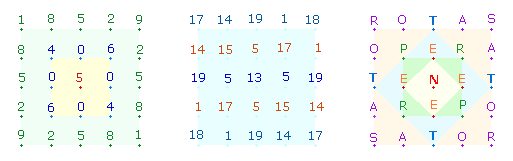
2. Die FS 35 der horizontalen Buchstaben beträgt die Hälfte ihrer ZS 70. Die Kenner des gematrischen Systems erkannten darin eine Parallele zum einstelligen 1x1-Modell des SATOR-Quadrats:

Nach Abzug der fehlenden Zahlen 3 und 7 des linken Quadrats bleibt von der Summe 45 der Zahlen 1-9 die Summe 35 übrig. Die Zahlen einer jeden Zeile bilden komplementäre Paare mit der Summe 10. Nach Häufigkeit (Hf) ergibt sich:

Erstellt: Januar 2013

domum

index