DAEDALUS und ICARUS
III. 13 A-Wörter am
Zeilenende
a)
Flügelsymmetrie
b)
8+6 Wörter
V. 13+1 A-Wörter:
Die Zahlen 13 und 14
a) Flügelsymmetrie
1. Die 13 mit A beginnenden Wörter am Zeilenende wurden im vorigen Kapitel eingeführt:
|
Nr. |
Zeile |
Wörter |
Buchstaben |
|||
|
1. |
2 |
AMORE |
5 |
|
|
|
|
2. |
6 |
ARTES |
5 |
|
|
|
|
3. |
10 |
AVENIS |
6 |
20 |
|
20 |
|
4. |
15 |
AURA |
4 |
|
|
|
|
5. |
19 |
ALAS |
4 |
|
|
|
|
6. |
20 |
AURA |
4 |
8 |
14 |
|
|
7. |
23 |
ADU-RAT |
6 |
+3 3+ |
|
|
|
8. |
27 |
ALAS |
4 |
|
4 |
|
|
9. |
31 |
ALTO |
4 |
17 |
|
|
|
10. |
33 |
ARTES |
5 |
|
13 |
|
|
11. |
34 |
ALAS |
4 |
|
|
|
|
12. |
36 |
ARATOR |
6 |
|
|
|
|
13. |
46 |
AURAS |
5 |
11 |
|
11 |
Die 13 Wörter sind kunstvoll in eine Ordnung gebracht. Ihre symmetrische Mitte bildet ADURAT als 7. Wort. Nach dem 4. Wort wird eine Gruppe von 7 Wörtern eingefügt. Deren symmetrische Struktur zeigt sich auf dreifache Weise:
·
ALAS ist Anfang, Mitte und Ende der 7 Wörter.
·
Die 27.
Zeile ist auch Symmetriemitte der 53 Zeilen.
·
Die Summe der Zahlen von 1-53 ist 27*53. 53 ist zweimal die Summe der angrenzenden
Zeilenpaare 19+34 und 20+33. Dies weist
auf zweimal 5:3 Radialelemente
des Tetraktyssterns hin sowie auf deren Kreisflächenentsprechung 3:1 und den 2*31
Buchstaben.
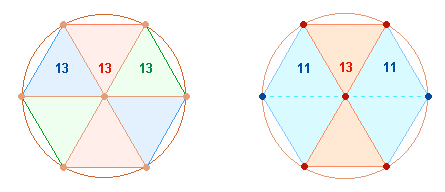
Zu den Wörtern AURA und ARTES in den Zeilen 20 und 33 stehen dieselben Wörter in chiastischer Stellung außerhalb des inneren Rahmens in den Zeilen 6 und 15. Ihre Summen 39 und 35 sind auf die Elemente zweier unterschiedlicher geometrischer Figuren im Hexagon zu beziehen:
|
|
Der Summe 74 = 39+35 entsprechen außerdem zweimal die 37 Elemente der Tetraktys.
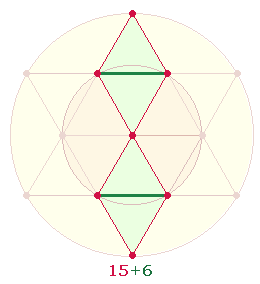
2. Die 5 symmetrischen Wörter innerhalb des Rahmens entsprechen den 5 Punkten des sanduhrförmigen Doppeldreiecks in der Doppelraute (DR). Die Zeilennummern 6 und 15 geben die Binnenelemente und Rahmenelemente der DR wieder:
|
|
Die Summe der 7 Zeilennummern ist 154 = 7*22, auf eine Zeilennummer entfällt die durchschnittliche Zahl 22, dies entspricht den 22 Elementen der DR, wenn man zwei Mittelpunkte zählt.
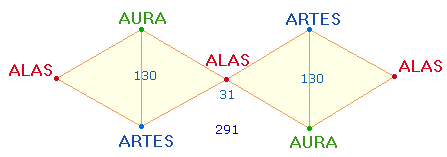
3. Nach Ovids Plan sind die 7 Wörter so auf den Punkten der DR einzutragen, daß eine vollkommene Symmetrie entsteht:
|
|
Die ZS 291 ist die Umkehrzahl zur Faktorensumme (FS) 219 der 7 Wörter und der ZS+FS von DAEDALUS und ICARUS:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
DAEDALUS |
64 |
43 |
107 |
12 |
43 |
55 |
162 |
|
ICARUS |
68 |
44 |
112 |
21 |
15 |
36 |
148 |
|
|
132 |
87 |
219 |
33 |
58 |
91 |
310 |
Die Summe 291+219 = 510 weist jedem der 30 Buchstaben den durchschnittlichen ZW+FW 17 zu.
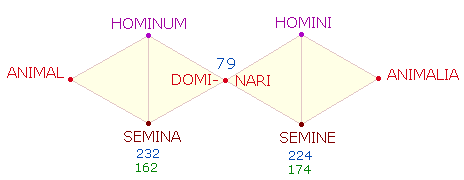
Als Modell könnten Ovid die 85 Zahlen zwischen den komplementären Primzahlen 13 und 97 gedient haben. Bereits in der Schöpfungsgeschichte (1, 76-88) gestaltete er eine DR mit 7 Wörtern, die die Silben MIN und NIM enthalten. Die ZS des mittleren Wortes DOMINARI erweist sich dabei als Komplementärzahl zu 31:yy
|
|
Beiden DR führen auch zu Ergebnissen als DR-Kreuze und Oktogone.
1. Nun befindet sich in Zeile 52 in Binnenposition ein weiteres ARTES. Die 4Werte der nunmehr 7+6+1 Wörter sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
AMORE |
49 |
39 |
88 |
14 |
16 |
30 |
118 |
|
AVENIS |
66 |
42 |
108 |
16 |
12 |
28 |
136 |
|
ADURAT |
62 |
51 |
113 |
33 |
20 |
53 |
166 |
|
ALTO |
45 |
40 |
85 |
11 |
11 |
22 |
107 |
|
ARATOR |
69 |
64 |
133 |
26 |
12 |
38 |
171 |
|
AURAS |
57 |
36 |
93 |
22 |
10 |
32 |
125 |
|
6 Wö. |
348 |
272 |
620 |
122 |
81 |
203 |
823 |
|
ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
AURA |
39 |
28 |
67 |
16 |
11 |
27 |
94 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
AURA |
39 |
28 |
67 |
16 |
11 |
27 |
94 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
7 W. |
291 |
219 |
510 |
149 |
76 |
225 |
735 |
|
13 W. |
639 |
491 |
1130 |
271 |
157 |
428 |
1558 |
|
+ ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
8 Wö. |
351 |
269 |
620 |
161 |
88 |
249 |
869 |
|
14 W. |
699 |
541 |
1240 |
283 |
169 |
452 |
1692 |
|
1558 = 2*19*41;1240 = 40*31; 1692 = 36*47; 452 = 4*113 |
|||||||
Die
7 Symmetriewörter bilden in der Tabelle eine
einzige Gruppe. Es zeigt sich, daß die ZS+FS von 6 und
8 Wörtern jeweils 620 ist. Auffällig ist, daß die ZS+FS 62+51 von ADU-RAT auch in den Gesamtsummen 620 und 510 in Erscheinung treten. Aus 6+8 Buchstaben bestehen DAEDALUS
und ICARUS, zwischen denen somit Gleichheit
besteht. Die Einzelziffern der ZS 62 und FS 51 sind als DR-Punkte
so erklärbar: 6+2 Punkte ist ihre höchste
Zahl mit 2 Mittelpunkten, 5+1 ihre niedrigste, da bei der Oktaederbildung
die äußeren 2 Punkte zu einem werden.
Die 4W-Summe 93 von ALAS ist dreimal so groß wie die ZS 31. Die Faktoren 31*3 geben ebenso die Punkteverteilung wieder wie die ZS 39 = 3*13 von AURA. Wie eng ALAS und AURA zusammengehören, zeigt sich in den angrenzenden 4W-Summen 93 und 94. Die Einzelziffern von 94 sind die ZW der Initialen von ICARUS und DAEDALUS. Die gesamte 4W-Summe 1692 enthält wie 94 den Faktor 47.
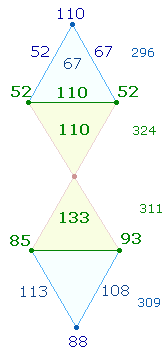
2. Wie kann man die Gleichheit der ZS+FS geometrisch zuordnen? Ovid deutet durch die doppelte Rahmenstruktur 4 Dreiecksflächen und 2 Querlinien sowie 8 Rahmenlinien an. Sie erbringt jedoch keine wirkliche Symmetrie. Daher ist die vorgegebene Struktur zu verlassen und eine Ordnung für jede Raute der DR zu wählen:
|
|
In Übereinstimmung mit der Buchstabenzahl von DAEDALUS und ICARUS enthält die obere Raute zweimal 4 ZS+FS, die untere zweimal 3. Gerechtfertigt erscheint diese Anordnung dadurch, daß bei Hinzufügung der FW die Gesamt-ZS+FS durch 13 teilbar ist, aber auch die FW der Einzelsummen selbst:
|
|
|
|
sm |
|
|
sm |
GS |
FW |
|
ZS+FS |
309 |
311 |
620 |
296 |
324 |
620 |
1240 |
42 |
|
FW |
106 |
311 |
417 |
43 |
16 |
59 |
476 |
28 |
|
sm |
|
|
1037 |
|
|
679 |
1716 |
70 |
|
FW |
|
|
78 |
|
|
104 |
|
|
|
1716 = 132*13; 78:104 = 26*(3:4); 42:28 = 14*(3:2) |
||||||||
132 ist die ZS 64+68 von DAEDALUS und ICARUS, aus 17+16 Elementen besteht das Achsenkreuz AK5.
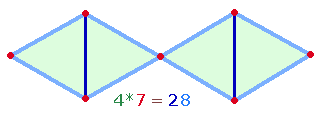
Mit 8+6 ZS+FS der DR lassen sich die 7 Wörter des Symmetriemodells zu einem DR-Kreuz verbinden:
|
|
Die ZS+FS 52 = 4*13 des Wortes ALAS ist auf die Zusammensetzung des Oktaeders aus 4 Doppeldreiecken beziehbar, die Einzelziffern der ZS+FS 229 auf die ZW 4 und 9 von DAEDALUS und ICARUS. Die zweimaligen ZS+FS 229+620 = 849 = 3*283 = FW 286 = 2*(11*13) geben ebenfalls die Bildung des Oktaeders aus 2 Rauten und 2 sanduhrförmigen Doppeldreiecken wieder.
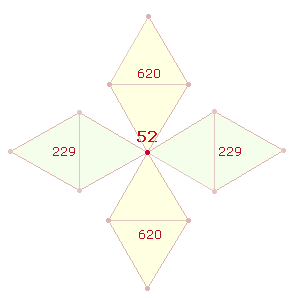
3. Die 4:2 Struktur der 6 Wörter des Außenrahmens ist auf 4 Punkte oder 4 Linien der Mittelbasis des Oktaeders und auf dessen beide
spiegelsymmetrischen Pyramidenspitzen beziehbar, die 8
Wörter den 8 Oktaederflächen zuzuordnen. Es
ist sinnvoller, die 4 Linien der Mittelbasis zu
wählen, damit die obere und untere Ecke feststehen und der Oktaeder nicht durch
weitere Ecken drehbar und veränderbar wird. Die 8
Wörter besetzen reihum die 2*4 Flächen.
Durch die so besetzten Oktaederelemente kommen aus je 5 Namen und ihren ZS+FS 4
Rauten zustande:
|
ZS+FS |
1 |
2 |
3 |
4 |
sm |
|
o.Ecke |
133 |
133 |
133 |
133 |
532 |
|
o. Fl. |
110 |
67 |
52 |
67 |
296 |
|
Mitte |
88 |
108 |
113 |
85 |
394 |
|
u. Fl. |
52 |
110 |
52 |
110 |
324 |
|
u.Ecke |
93 |
93 |
93 |
93 |
372 |
|
|
476 |
511 |
443 |
488 |
1918 |
|
1918 = 2*7*137 > FW 146 = 2*73 |
|||||
Die Summe 1918 gibt in der Addition 19+18 die 37 Elemente der Tetraktys wieder, die Einzelziffern des Faktors 73 7+3 Punkte der Tetraktys.
Die FW 26+34 = 60 der zwei ZS+FS 133+93 = 226 weisen auf 26
Elemente des Oktaeders und 2*17 Elemente
zweier Oktaederhälften hin, die Summe 60+226 = 286 = 2*11*13
auf die Zusammensetzung des Oktaeders aus den
Elementen von 2*(11+13) = 22+26 Elementen
der Raute und des sanduhrförmigen Doppeldreiecks. Die dreistellige ZS 226 kann als Kontraktion von 22 und 26
verstanden werden.
Radialelemente und Durchmesserelemente
begründen das Prinzip zweier Hälften und des Ganzen. Auf den vorliegenden Fall
angewendet ist die ZS+FS
der beiden Hälften 133+296+394
= 823 und 93+324+394 = 811. Zusammen
mit der ZS 1240 des ganzen Oktaeders ergibt sich
die Summe 823+811+1240 = 2874 =
2*3*479 > FW 484 = 4*11² >26,
an deren Einzelziffern man die 21 Elemente
der DR erkennen kann: 2 Querlinien, 8
Rahmenlinien, 7 Punkte und 4 Flächen:
|
|
4*11² = 22*22 weist auf die Zusammensetzung des Oktaeders
aus 4 Rauten hin.
Erstellt: Februar 2018