Strukturen in Dädalus und
Ikarus
I.
Symmetrie und syntaktische Struktur
II. Struktur der 13 mit A
beginnenden Wörter am Zeilenende
a) Tabelle
c) Die Zahlenwerte der 13 Wörter
III. 7 A-Wörter in der Doppelraute
Die Präposition A in zwei
Versen
Ovids
Modell von 84 Komplementärzahlen
I. Symmetrie und syntaktische
Struktur
|
5 |
5 |
10 |
7 |
7 |
14 |
5 |
|
27 |
26 |
|||||
|
|
22 |
21 |
|
|||
|
Stellenangabe |
Zeilenzahl |
|
||||||
|
1-5 |
|
|
|
|
5 |
|
Einleitung: Entschluß zur Flucht |
|
|
6-27 |
|
|
|
|
|
|
|
Vorbereitung (22 Z.) und Abflug |
|
|
6-20 |
|
6-10 |
|
5 |
|
|
Bau der Flügel |
|
|
|
6-13 |
11-13 |
|
|
8 |
|
technische
Herstellung |
|
|
|
|
13-18 |
27 |
10 |
|
6 |
Das
Spiel des Ikarus |
|
|
|
18-20 |
|
|
|
3 |
|
Probeflug des Vaters |
|
|
21-34 |
|
|
|
|
|
|
Die Sorge des Vaters für den Sohn |
|
Mittelachse (27) |
21-27 |
|
|
14 |
7 |
|
a) Anweisungen und Anpassung der Flügel |
|
|
28-48 |
|
|
|
|
|
|
Flug und Absturz (21 Z.) |
|
|
|
|
28-34 |
|
|
|
7 |
|
b) Die
Gefühle des Vaters, Vergleich, Flug Vater u. Sohn |
|
|
35-48 |
35-38 |
|
|
|
4 |
|
Der Eindruck des Fluges auf drei Beobachter |
|
|
|
38-40 |
|
26 |
14 |
3 |
|
Die Beschreibung des zurückgelegten Weges |
|
|
|
41-45 |
|
|
|
5 |
|
Ikarus fliegt zu hoch, das Wachs schmilzt |
|
|
|
45-48 |
|
|
|
4 |
|
Ikarus stürzt ab, das Meer erhält seinen Namen |
|
49-53 |
|
|
|
|
5 |
|
|
Klage des Vaters; das Land erhält den Namen des Sohnes |
1. Die Zeilen 6-20 und 35-48 sind als zusammenhängende Texteinheiten
konzipiert. Mit tum
lino in Zeile 11 beginnt zwar ein neuer Satz, aber das vorherige Geschehen wird
fortgesetzt. Bezugspunkt für diese Einteilung ist die Numerierung
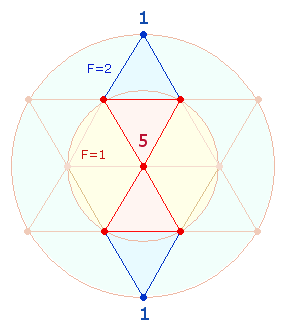
konzentrischer Elemente von 1-5:
|
|
Wenn der Mittelpunkt einer Seite zugeordnet wird,
kann von außen nach innen die Einteilung 5+10
vorgenommen werden.
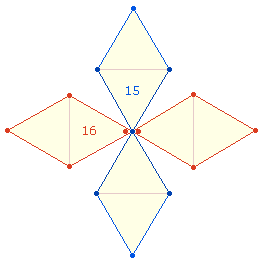
Die Texteinheiten werden je zweimal durch
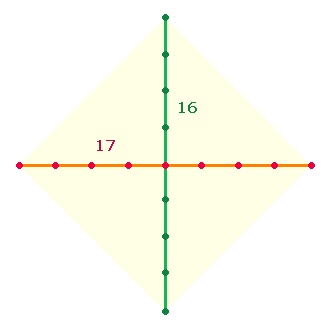
Themenwechsel in der Zeilenmitte verknüpft. Zählt man jedes Thema in ganzen
Zeilen, erweitert sich die Zahl auf 17+16.
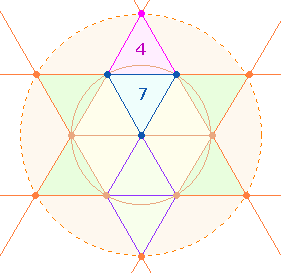
Elementen eines Achsenkreuzes, das als ein Modell für die Flugorientierung
angesehen werden kann:
|
|
Hier kann ein Blick auf die Zahlenwerte und Faktorenwerte (FW) von DAEDALUS und ICARUS hilfreich sein:
|
|
D |
A |
E |
D |
A |
L |
U |
S |
sm |
I |
C |
A |
R |
U |
S |
sm |
GS |
|
ZW |
4 |
1 |
5 |
4 |
1 |
11 |
20 |
18 |
64 |
9 |
3 |
1 |
17 |
20 |
18 |
68 |
132 |
|
FW |
4 |
1 |
5 |
4 |
1 |
11 |
9 |
8 |
43 |
6 |
3 |
1 |
17 |
9 |
8 |
44 |
87 |
|
|
|
|
|
|
|
|
|
|
107 |
|
|
|
|
|
|
112 |
219 |
|
64:68 = 4*( |
|||||||||||||||||
Der Faktor 29 der FS 87 ist eine Erklärung für die
Textgliederung von 15+14 Zeilen.
Beachtenswert sind auch die beiden Initialen DI mit der ZS 13 als kontraktierte Pluralform von DEUS – Gott. Eine Anspielung darauf ist in der Meinung der Beobachter zu erkennen, die
Vorüberfliegenden seien Götter (credidit esse deos, Z.38).
2. In konzentrischen Anordnungen gehört
die Symmetriemitte beiden Seiten an, weswegen eine Doppelzählung von einem und
zwei Mittelpunkten zur vollständigen Erfassung der Elemente erforderlich ist.
Dies trifft auch auf die Elemente des Oktaeders zu, der aus einem Doppelrautenkreuz gebildet werden kann: Zur äußeren Zahl von 26 Elementen (6 Ecken, 12 Kanten, 8 Flächen) kommt noch das Volumen hinzu.
Auf diese Weise ergibt sich die Doppelzählung von 27+26 = 53. Ein DR-Kreuz kann als eine Gestalt mit ausgebreiteten
Flügeln angesehen werden.
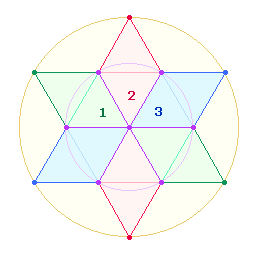
Eine zusammengesetzte Zahl besitzt auch in ihren
Einzelziffern Relevanz. Im Modell des Tetraktyssterns gibt es eine Analogie
zwischen den Elementen seiner doppelten Konzentrik und den Flächen der dazu
gehörenden Kreise:
|
|
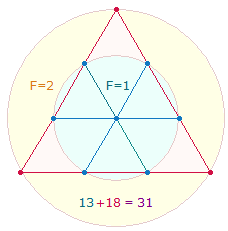
Die Grafik zeigt die
Durchmesserlinie einer Doppelraute. Das Kreisflächenverhältnis des äußeren Kreises zum inneren Kreis beträgt 3:1. Es kann durch (2+3):3 Radialelemente auf jeder Seite oder 9:5 Durchmesserelemente wiedergegeben werden. Die Zahlen 13 und 31 werden im weiteren Verlauf noch eine wichtige
Rolle spielen.
II. Die Struktur der mit A beginnenden Wörter am Zeilenende
|
Nr. |
Zeile |
Wort |
B.zahl |
Bu. |
Bu. |
Bu. |
|
1. |
2 |
AMORE |
5 |
|
|
|
|
2. |
6 |
ARTES |
5 |
|
|
|
|
3. |
10 |
AVENIS |
6 |
20 |
|
20 |
|
4. |
15 |
AURA |
4 |
|
|
|
|
5. |
19 |
ALAS |
4 |
|
|
|
|
6. |
20 |
AURA |
4 |
8 |
14 |
|
|
7. |
23 |
ADU-RAT |
6 |
+3||3+ |
|
|
|
8. |
27 |
ALAS |
4 |
|
4 |
|
|
9. |
31 |
ALTO |
4 |
17 |
|
|
|
10. |
33 |
ARTES |
5 |
|
13 |
|
|
11. |
34 |
ALAS |
4 |
|
|
|
|
12. |
36 |
ARATOR |
6 |
|
|
|
|
13. |
46 |
AURAS |
5 |
11 |
|
11 |
Auffällig sind 13 mit A beginnende Wörter am Zeilenende. Das Wort ALAS in Zeile 27 ist
Symmetriemitte eines inneren Rahmens, der durch zwei weitere ALAS begrenzt wird. Der Rahmen wird verstärkt durch die folgende 20. bzw. vorangehende 33. Zeile, so daß die Addition
jedes konzentrischen Zeilenpaares 53 beträgt, also einen Teil der
Gesamtsumme 27*53 der Zahlen von 1-53.
Im inneren Rahmen befinden sich 7, außerhalb 6 Wörter. Die Buchstabenzahl des äußeren und
inneren Rahmens ist jeweils die 31 (14+4+13; 20+11), also die Umkehrung der Zeilenzahl 13. Die Zeile 23 (7.) bildet die Symmetrieachse
der 13 Zeilen. Teilt man das Mittelachsenwort ADU-RAT, ergeben sich wiederum zwei Hälften von jeweils 31 Buchstaben. ADURAT wird so zum zentralen Motiv der Geschichte mit
möglicherweise mehreren Bedeutungsebenen.
1. Die ermittelte Ordnung ist ohne
Zuhilfenahme von geometrischen und gematrischen Gesichtspunkten nicht verstehbar. Geometrischer
Ausgangspunkt ist der Tetraktysstern, der zwei Tetraktys
und drei Doppelrauten enthält:
|
|
Dem oberen Dreieck einer Raute
entspricht der Buchstabe A, dem unteren der Buchstabe V. Ein Achsenkreuz aus zwei Doppelrauten (DR) kann durch Faltung der Querlinien und Vereinigung der Eckpunkte zu einem Oktaeder zusammengefügt werden:
|
|
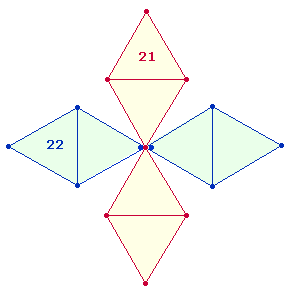
Eine Raute besteht aus 4 Punkten, 5 Linien und 2
Dreiecksflächen, zusammen aus 11 Elementen, eine DR entweder aus 21 Elementen bei einem oder aus 22 Elementen bei zwei Mittelpunkten.
Beide Zählweisen sind als Texteinheiten in die formale Gliederung der 53 Zeilen eingepaßt.
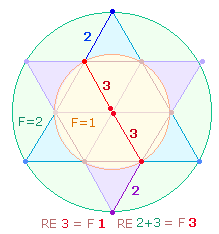
2. Eine wichtige Rolle spielen die
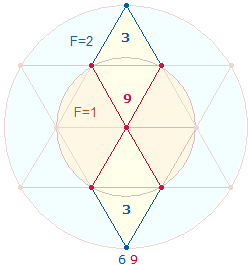
Rahmenelemente der Doppelraute (DR). Bei 1 Mittelpunkt sind es 29, bei 1+2 Mittelpunkte 31 Elemente:
|
|
Indem ein DR-Kreuz das stilisierte
Modell einer Gestalt mit ausgebreiteten Flügeln sein kann, sind zweimal 31 Buchstaben auf Dädalus und Ikarus zu beziehen. Es
ist in sachlicher Hinsicht stimmig, daß dem Menschen ein Mittelpunkt zugewiesen
wird und an seinem Körper zwei Flügel angeheftet werden.
Die
Gestalt der DR ist durch die Punktestruktur 313 vorgegeben. Jeder
Flügel kann daher von innen her zweistellig als 13 und von außen her als 31 verstanden werden.
Der Faktor 31 ist auch in den 4Werten von DAEDALUS und ICARUS enthalten:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
DAEDALUS |
64 |
43 |
107 |
12 |
43 |
55 |
162 |
|
ICARUS |
68 |
44 |
112 |
21 |
15 |
36 |
148 |
|
|
132 |
87 |
219 |
33 |
58 |
91 |
310 |
|
a(3) e(1) i(1) u(2) |
V |
7 |
57 |
|
c(1) d(2) l(1) r(1) s(2) |
K |
7 |
75 |
Die Umkehr-ZS 57 und 75 sind geeignet, den Sohn
als Abbild des Vaters zu sehen. 57 ist die ZS von PATER. Bezieht man die Einzelziffern auf die 7 Punkte der DR, bedeuten 5 Punkte des hexagonalen
Bereichs zu den 7 Punkten der ganzen DR das Kreisflächenverhältnis 1:3 und 7:5 Punkte
das Verhältnis 3:1. Diese
ZS-Verhältnisse boten Ovid eine weitere willkommene
Konstruktionsidee.
Ovid
setzt die Wörter ans Zeilenende, weil die äußeren Dreiecke der DR wie
beim A in einer Spitze enden und so die Flügelenden darstellen können.
3. Die
Symmetrie zweier Flügel ist im Wort A-L-A selbst angelegt. Der Zahlenwert (ZW) von A ist 1, von L 11. Nebeneinander
geschrieben ergibt sich viermal eins: 1111, was man als 11+11 oder 11*11, also als eine DR interpretieren kann.
Die 13 Wörter der Tabelle
enthalten 21 A und 5 V (ZW 20). Das ergibt die Zahlensumme (ZS) 121 = 11*11. Die 26 Buchstaben bilden die
Umkehrung von 62 und entsprechen der Zahl der Oktaederelemente.
4. Die drei
Hexagonachsen bestehen aus 7 Punkten und 6 Linien, zusammen 13
Elementen, der Rahmen einer Tetraktys aus 9 Punkten und 9 Linien, zusammen 18
Elementen: Beide zusammen bilden ein Gerüst, das auch für die Anfertigung von
Flügeln erforderlich ist:
|
|
Die
Hinzufügung von 18 Elementen bewirkt die Umkehrung der Zahl 13 zu 31. Dem entspricht die ZS von ALA und ALAS, da S den ZW 18 hat. Der Plural weist auf je zwei Flügel der
beiden Fliegenden hin, die durch die ZS 62 von ADURAT zusammengefaßt werden.
5. Eine DR besteht aus zweimal drei Punkten und einem oder zwei Mittelpunkten. Wählt man zwei Mittelpunkte,
ergibt sich die Umkehrstruktur 31/13 oder die Parallelstrukturen
31/31, 13/13. Diese Entsprechungen
können auch als Gleichung formuliert werden, z.B. 1+3 = 4 und dreistellig zur Zahl 134 zusammengesetzt werden. Faßt man die 7 Punkte
zusammen, tritt als 1 ein zweiter Mittelpunkt hinzu, was als Bedeutung
die Zahlen 17 und 71 wiedergeben können:
|
|
|
Die
Komplementärzahlen zu 17 und 71 sind 93 = 3*31 und 39 = 3*13. Die Einzelziffern der Faktoren 3*13 geben die Anordnung der
7 DR-Punkte wieder.
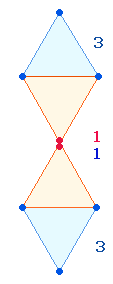
6. Ein sanduhrförmiges Doppeldreieck
besteht aus 13 Elementen. Es sind also zwei mehr als die 11 Elementen der Raute, sie können durch zwei A dargestellt werden können.
Beide Figuren sind im Hexagon und in der DR zu
sehen:
|
|
Dem Wort ALA ist also sowohl die Zahl 11 als auch 13 zuzuordnen.
Bemerkenswert sind 22+26 als ZS der
Initialen IN-RI und der Buchstabenzahlen der historischen und der biblischen Kreuzesinschrift.
7. Nach den bisherigen geometrischen
Grundlagen bietet sich die günstige Gelegenheit, eine erste gematrische Bilanz
zu ziehen:
· ALA hat die ZS 13, ALAS die ZS 31. Die beiden A bezeichnen die Flügel, das L in der Mitte den Körper des Fliegenden oder Flugfähigen.
· Der Fliegende mit
ausgebreiteten Flügel kann durch die 31 Rahmenelemente eines DR-Kreuzes dargestellt werden.
· Die angelegten
Flügel lassen sich mit dem Körper des Oktaeders vergleichen, der aus einem DR-Kreuz zusammengefügt ist:
|
|
· Betrachtet man den
Oktaeder von oben auf seine Spitze, ist dieser der Mittelpunkte für zwei
Doppeldreiecke aus 13 Elementen,
was auch für die untere Spitze gilt, sodaß sich insgesamt 4*13 = 52 Elemente ergeben, die doppelte
Zahl der 26 Oktaederelemente. Betrachtet man
ihn von der quadratischen Mittelbasis zur oberen und unteren Ecke hin, besteht
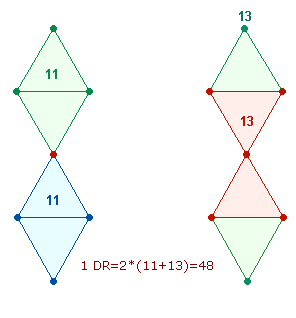
er rundum aus vier Rauten, also aus 4*11 = 44 Elementen. Beide Zusammensetzungen können entweder zu 2*(11+13) = 48 kombiniert oder zu 4*(11+13) = 96 addiert werden.
8. Da die zwei Endpunkte einer DR – als Erweiterung der 5
Punkte des hexagonalen Doppeldreiecks – bei
der Oktaederbildung vereinigt werden, hat die Primzahl 151 eine besondere Symbolbedeutung für die DR:
|
|
Die Addition der 13
Zeilennummern ergibt 302 =
2*151, also eine Symbolzahl für zwei
Flügel oder ein DR-Kreuz.
c) Die Zahlenwerte der 13 Wörter
1. Die Zahlensummen (ZS) der 13 Wörter sind folgende:
1. amore (49)
5
(5) 49 (49)
2. artes
5
(10) 60
(109)
3. avenis
6
(16) 66
(175)
4. aura
4
(20) 39 (214)
5. alas
4
(24) 31 (245)
6. aura
4
(28) 39 (284)
7. adurat
6
(34) 62 (346)
8. alas
4
(38) 31 (377)
9. alto
4
(42) 45
(422)
10. artes
5
(47) 60 (482)
11. alas
4 (51) 31
(513)
12. arator
6 (57) 69
(582)
13. auras
5 (62) 57 639 = 9*71
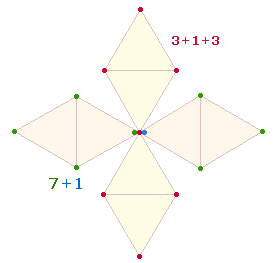
Das ZS-Verhältnis von 6 zu 7 Wörtern ist 284:355 = 71*(4:5). 4 Durchmesserelemente sind mit 6 Punkten der hexogonalen Erweiterung und 5 hexagonale
Achsenelemente mit 7 hexagonalen Punkten verknüpft. Das dadurch wiedergegebene Kreisflächenverhältnis ist 2:1.
ADURAT – versengt hat die doppelte ZS von ALAS. Hiermit wird die Hauptgefahr veranschaulicht, die den Flügeln droht, wenn
sie den Weg der Mitte (7. Wort) verlassen. Der Faktorenwert (FW) von 639 ist 77 = 7*11. Die beiden Produktzahlen sind auf die 11 Elemente der Raute im Hexagramm beziehbar:
|
|
Das Verhältnis von 7:(7+4) Rautenelementen gibt das Kreisflächenverhältnis 1:3
wieder. Wie oben schon dargelegt
wurde, können die Einzelziffern von 71 als 7+1 Punkte einer DR der als 7+1 Rahmenelemente einer einzelnen Raute verstanden werden.
2. Die Eigenart von zwei verschiedenen Symmetriemittelpunkten
hat ihren Grund darin, daß die innere Gruppe von 7 Wörtern nach dem 4. Wort erfolgt und danach nur noch 2 Wörter folgen. Weiterhin ist festzustellen, daß ARTES ein drittes Mal in Binnenposition (Z.52)
erscheint und so ein weiteres Modell von 14 Wörtern
hinzukommt.
Eines der Modelle besteht in der
Besetzung der 13 Punkte des DR-Kreuzes. Hierzu sind alle 4Werte der 13 Wörter erforderlich:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
AMORE |
49 |
39 |
88 |
14 |
16 |
30 |
118 |
|
ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
AVENIS |
66 |
42 |
108 |
16 |
12 |
28 |
136 |
|
AURA |
39 |
28 |
67 |
16 |
11 |
27 |
94 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
AURA |
39 |
28 |
67 |
16 |
11 |
27 |
94 |
|
ADURAT |
62 |
51 |
113 |
33 |
20 |
53 |
166 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
ALTO |
45 |
40 |
85 |
11 |
11 |
22 |
107 |
|
ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
ALAS |
31 |
21 |
52 |
31 |
10 |
41 |
93 |
|
ARATOR |
69 |
64 |
133 |
26 |
12 |
38 |
171 |
|
AURAS |
57 |
36 |
93 |
22 |
10 |
32 |
125 |
|
|
639 |
491 |
1130 |
271 |
157 |
428 |
1558 |
|
ARTES |
60 |
50 |
110 |
12 |
12 |
24 |
134 |
|
|
699 |
541 |
1240 |
283 |
169 |
452 |
1692 |
|
699 = 3*233; 1692 = 36*47; 452 = 4*113 |
|||||||
Die ZS+FS 1240 = 40*31 ist deshalb von besonderer Bedeutung, weil sie
der FW der 5-stellig zusammengesetzten Faktoren des Wortes NET – er webt ist: 13*5*19 >13519 = 11*1229 >1240.
Die Einzelziffern der ZS 699 sind auf 6+9 Rahmenelemente der DR und 9 vertikale Achsenelemente beziehbar, die 3 Schnittpunkte
werden dabei doppelt gezählt:
|
|
Den Einzelziffern des Faktors 233 entsprechen die
Radialelemente der DR, die das Kreisflächenverhältnis 3:1 wiedergeben.
Die Einzelziffern der FS 541 bezeichnen 9 Durchmesser- und 9+1 Radialelemente der DR-Zickzacklinie. Der Differenzbetrag 158 zwischen
der FS 541 und der ZS 699 ist auf 8 Rahmenlinien
der DR und 8 Flächen des Oktaeders
beziehbar. Bei der Oktaederbildung fallen die zwei äußeren Punkte zu einem
zusammen, 5 Punkte gehören dem hexagonalen Bereich an und
bilden 5 der 6 Oktaederecken.
Die Bedeutung des Wortes ADURAT ermißt sich daran, daß die ZS+FS 113 auch Faktor der ZS+FS 1130 der 13 Wörter ist. Auch die FW1/2-Summe 452 enthält den Faktor 113.
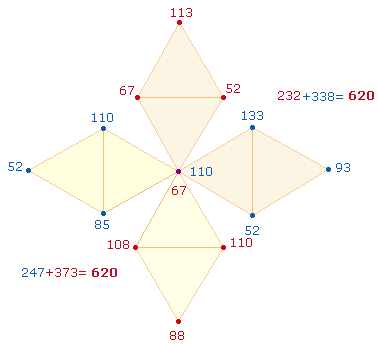
3. Man kann es Ovid zutrauen, daß er
sinnvolle Zahlenverhältnisse berechnet hat. Wie man ein Achsenkreuz durch Winkelverschiebung zu einem Quadrat machen kann, so ein DR-Kreuz zu einem Oktogon. Zu ermitteln ist, ob sich zwei Rautenpaare
finden, die ein Zahlenverhältnis zueinander bilden. Dies ist bei den ZS+FS der Fall:
|
|
Unter Hinzunahme des 14. Wortes ARTES (110), das den zweiten Mittelpunkt besetzt, sind die 4W-Summen der zusammengehörigen Rautenpaare jeweils gleich.
Neu bearbeitet: April 2017, Februar 2018