Die Zahl 619: der unsichtbare
Mittelpunkt
I.
Einleitung
I. Einleitung
1. Am Zustandekommen des SATOR-Quadrats sind viel Komponenten und Prinzipien beteiligt. Zu den grundlegenden Prinzipien gehören Symmetrie und Symmetriemittelpunkt. Symmetrische Elemente sind immer doppelt zu zählen und bilden daher gerade Zahlen. Symmetriemittelpunkte und symmetrische Elemente begründen die Abfolge von ungeraden und geraden Zahlen.
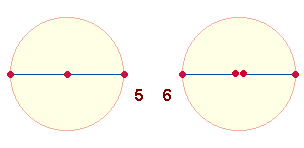
2. In der raumzeitlichen Dimension ist die Addition 1+2 die kleinste Einheit von ungerader und gerader Zahl, um ein Maß darzustellen:
|
|
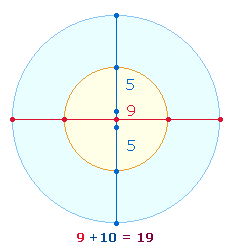
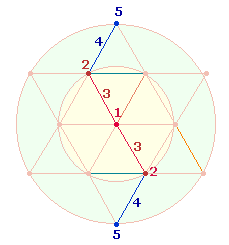
Die Grundlage der Symmetrie ist die Kreisteilung. Sie bewirkt zwei Radialmaße, demnach zweimal die Zahl 3, zu sehen ist aber nur ein Mittelpunkt. Nun haben sowohl die numerische Gestalt des Durchmessers (der Kreisachse) als auch zwei Radialmaße ihre Eigenberechtigung. Um beiden gerecht zu werden, gehört zum ontologischen Sinngefüge des Zahlensystems der Doppelaspekt von einem und zwei Mittelpunkten:
|
|
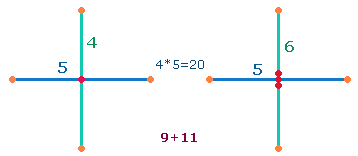
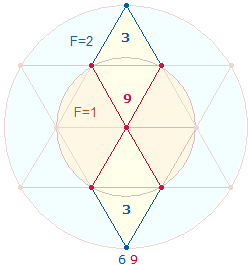
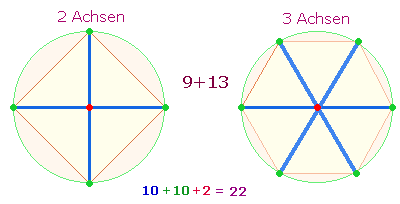
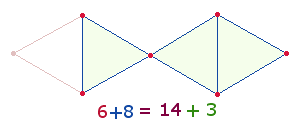
3. Das Problem tritt deutlicher hervor bei Achsenkreuzen: Jede Achse besteht aus einer ungeraden Zahl von Elementen, aber sichtbar ist nur ein Mittelpunkt. Als komplementärer Ausgleich kommt ein zweites Achsenkreuz in Frage, dessen zweite Achse zwei Radialmittelpunkte enthält:
|
|
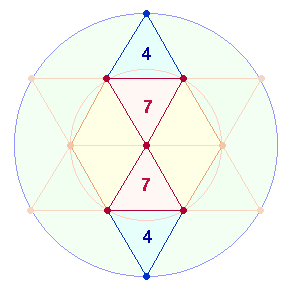
Durch diesen Ausgleich besteht nun jede Achse aus 5 Elementen. Der eigentliche Mittelpunkt gehört jedoch auch in der zweiten Grafik der Horizontalachse an. Die beiden komplementären Achsenkreuze bestehen also aus zwei Durchmessermittelpunkten und zwei Radialmittelpunkten.
Dennoch bleibt das Problem bestehen, daß jede Achse ihren eigenen Mittelpunkt besitzt. Man kann nun wie bei der Kreisachse den Doppelaspekt rechnen: 5+5 = 10; 5+4 = 9. Dabei wird im ersteren Fall der zweite Punkt hinzugedacht. Aber es scheint hier Sichtbares und Unsichtbares zusammenzutreffen:
Die sichtbare
Welt erhält durch ein unsichtbares Element ihre Vollständigkeit.
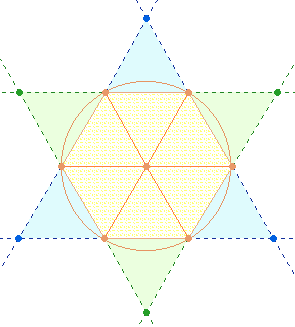
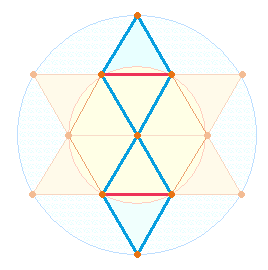
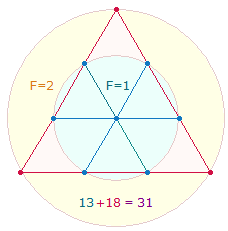
4. Zur vollen Realität gehört also ein unsichtbares Element, das der Mensch einerseits hinzufügen muß, andererseits in den Zahlen selbst vorfindet. Das herausragendste Beispiel ist das Hexagramm (der Tetraktysstern), sofern man zugesteht, daß es eine Erweiterung aus Kreis und Hexagon darstellt:
|
|
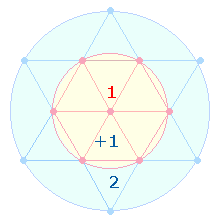
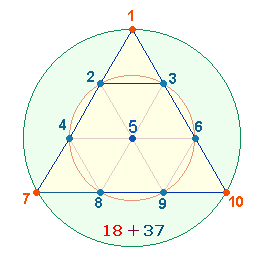
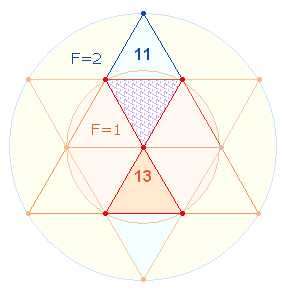
Man könnte das Hexagramm als eine geometrische Figur neben anderen ansehen, wenn sie nicht in zwei Dreiecken je 10 Punkte enthielte. Diese schreiten im Sinne eines Zahlendreiecks von 1-4 fort. Schreibt man die vier Zahlen als 1234 nebeneinander, sind ihre Faktoren 2*617. Nun besteht ein Hexagon aus 7 Punkten und die Erweiterung aus 6 Punkten. Im Faktor 617 folgt nach der 6 eine 1, die einen unsichtbaren Mittelpunkt anzeigt, der zur Ziehung eines äußeren Kreisbogens erforderlich ist und dem hexagonalen Mittelpunkt entspricht. Die Einzelziffern genügen der Gleichung 6+1=7 wie 2+1 = 3. Die äußeren 6 Punkte stellen 2 Kreisflächeneinheiten des äußeren Kreisrings dar, der Mittelpunkt 1 Kreisflächeneinheit des Hexagons, die Zahl 7 faßt 6+1 zu 3 Flächeneinheiten zusammen:
|
|
Die Einzelziffern der zweiten Zahl 617 können sich auf 6+1 Punkte des Hexagons und 6+1 Punkte des äußeren Kreises beziehen und geben dann das Kreisflächenverhältnis 1:3 wieder. Auf diese Weise ergeben sich 2+1+3+1+3 = 10 Kreisflächeneinheiten.
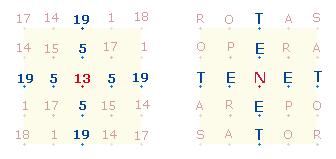
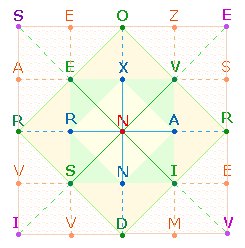
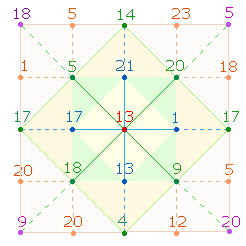
1. Der Faktorenwert (FW) von 2*617 ist 619. Die Zahlensummen (ZS) 61, 19 und 69 im SATOR-Quadrat sind an dieser Zahl 619 orientiert:
|
SATOR |
AREPO |
TENET |
OPERA |
ROTAS |
|
69 |
52 |
61 |
52 |
69 |
Hinzu kommt das TENET-Kreuz:
|
|
2. Das Achsenkreuz enthält einen unsichtbaren Mittelpunkt. Die Doppelzählung von einem und zwei Mittelpunkten ergibt 109 + (61+61) = 231 = 21*11. Die Zahl 109 ist zusammengesezt zu denken aus 10 Radialelementen und 9 Durchmesserelementen der Doppelraute (DR), die sich innerhalb der beiden konzentrischen Kreise befindet. Die beiden Zählweisen werden hier durch ein Achsenkreuz dargestellt:
|
|
3. Der Tetraktysstern findet seine Vollendung in der Dreidimensionalität des Oktaeders, der durch ein Achsenkreuz zweier DR gebildet werden kann:
|
|
Der Rahmen einer DR besteht aus 7 Punkten und 8 Linien, zusammen aus 15 Elementen. Unter Annahme eines unsichtbaren Mittelpunkts besteht ein DR-Rahmen aus 30 Elementen. Um zur Zahl 61 zu gelangen, ist ein DR-Kreuz mit 3 Mittelpunkten erforderlich. Die Einzelziffern von 31+30 Elementen stimmt sinnvoll mit der Aufteilung der DR-Punkte in 3+1+3 zusammen sowie mit den Einzelziffern 6+1 für eine DR.
Gestützt wird diese DR-Kreuz durch die ZS und Faktorensummen (FS) der Zahlen 1-30 und 1-31:
|
|
1-30 |
1-31 |
sm |
|
ZS |
465 |
496 |
961 |
|
FS |
294 |
325 |
619 |
Die FS 619 ist identisch mit dem FW von 1234, die ZS 961 eine Umkehrform der Einzelziffern.
4. Die Zahl 69 ist einerseits in 619 enthalten, andererseits entsteht sie aus den FW der Umkehrzahlen 16 und 61: 8+61 = 69. 1+6 und 6+1 Punkte gibt die Entwicklung des Tetraktyssterns genau wieder, wie oben dargelegt wurde. Aus 8+(6+1) = 15 kann man die 8 Linien und 7 Punkte des DR-Rahmens ablesen. Der DR-Rahmen kann eingeteilt in 6 Erweiterungselemente und 9 hexagonale Elemente:
|
|
Diese Aufteilung gibt das Kreisflächenverhältnis 2:1 wieder. In der Zahl 619 kommt zu den 6 Elementen ein unsichtbarer (zweiter) Mittelpunkt hinzu, wodurch das Verhältnis 3:1 entsteht.
Der FW der vierstellig zusammengesetzen Zahl 1661 = 11*151 ist 162. Die Addition 1661+162 ergibt die Primzahl 1823. Zweistellig ist 18 die FS 11+7 von 11+12. Die Einzelziffern der beiden Zahlen bedeuten in trinitarischem Sinn die erste und zweite Person (11) und die erste Person und zweite + dritte Person (12). Dieselben Einzelziffern kommen durch die Zahl 16 und ihrem FW 8 zustande. Denn das Verhältnis von 8 und 16 zweifach: entweder 8*(1:2) oder 8*(1:1), wenn den FW als Teil des ZW betrachtet.
1. Der unsichtbare Mittelpunkt bezieht sich besonders, wenn nicht ausschließlich, auf Achsenkreuze und (zwei) konzentrische Kreise. Ein Beispiel hierfür sind die Primzahlen 113 und 131, zu lesen als 1+13 und 13+1. Der Tetraktysstern besteht aus 7 hexagonalen und 6 Erweiterungspunkten. Ein Kreis über die 6 Erweiterungspunkte versieht diese mit einem eigenen Mittelpunkt. Somit bedeuten 7+7 Punkte das Kreisflächenverhältnis 1:3 oder 3:1. Die Faktoren 7*11 der Zahl 77 sind in der DR erkennbar:
|
|
Ein Dreieck besteht aus 7 Elementen, die dem hexagonalen Bereich mit 1 Flächeneinheit angehört, die Raute aus 11 Elementen, die beide Bereiche umfassen und daher 3 Flächeneinheiten wiedergeben.
Das Verhältnis 1:3 wird auch sichtbar, wenn man beide Zahlen zweistellig aufteilt:
|
113 |
11 |
13 |
13 |
37 |
131 |
13 |
31 |
11 |
55 |
|
FW |
11 |
13 |
13 |
37 |
|
13 |
31 |
11 |
55 |
Wenn man die 10 Punkte der Tetraktys numeriert, befindet sich die Summe 37 im hexagonalen und die Gesamtsumme 55 im ganzen Bereich des umschlossenen Tetraktysstern:
|
|
Die identischen FS sind der zweiten Tetraktys zuzuordnen.
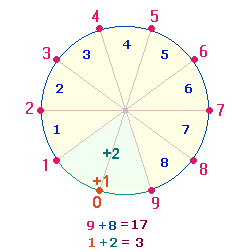
2. Die Summe 113+131 = 244 wechselt von den Punkten zu den Maßeinheiten. 2+8 Maßeinheiten werden in einer Kreisformation der Grundzahlen von 1-9 sichtbar mit der 0 als Anfangspunkt:
|
|
In der DR erscheinen die 2 Maßeinheiten zwischen 9 und 1 als Querlinien zu den 8 Rahmenlinien:
|
|
Die zwei Querlinien gehören zum hexagonalen Bereich, daher vertreten 2:8 Linien das Kreisflächenverhältnis 1:3.
3. Die Faktoren 4*61 von 244 sind auf zweimal 7 Punkte des Tetraktyssterns und seiner zwei konzentrischen Kreise sowie eines DR-Kreuzes beziehbar.
1. Ein besonderes Beispiel des unsichtbaren Mittelpunktes ist die lateinische Kreuzesinschrift:
|
|
Die aus zweimal zwei Wörtern bestehende Inschrift kreuzt sich im ersten A von NAZARENUS: Ein A wird unsichtbar. Die ZS und FS der gesamten Inschrift ist 326 = 2*163 = FW 165 und 225 = 15*15 = FW 16. Die Primzahl 163 gibt die 10 Punkte einer Tetraktys wieder: Mittelpunkt, 6 Hexagonalpunkte und 3 Eckpunkte, zweimal 15 die Rahmenelemente eines DR-Kreuzes. Bei zwei ineinandergeschobene Tetraktys und einem DR-Kreuz kann jeweils ein Mittelpunkt als unsichtbar bezeichnet werden. Den somit 19 Tetraktyspunkten und 29 Rahmenelementen entsprechen die Faktoren 19*29 der ZS+FS 551.
Die Faktoren 19*29 = FW 48 sind folgendermaßen interpretierbar: Der Zahl 19 entspricht die oben gezeigte Grafik einer Kreisanordnung von 10 Punkten, von 0 angefangen, dann 9 weitere Punkte, 2+9 Punkte liegen vor, wenn sie von 0-10 linear verlaufen. In jedem Fall begrenzen einmal 10 und einmal 11 Punkte 10 Maßeinheiten. Dies zeigt sich in den FW der Umkehrungen 91 = 7*13 = FW 20 und 92 = 4*23 = FW 27. Die FW 20 und 27 entsprechen 20 Maßeinheiten und 27 Punkten:
|
|
Wenn für jede Achse ein Mittelpunkt gezählt wird, erhöht sich die Gesamtzahl von 12 auf 15. Die Doppelzählung von Punkten und Maßeinheiten ergibt 27+20 = 47. Die ZS+FS der Umkehrungen betragen (48+48)+(183+47) = 326, die ZS der Kreuzesinschrift.
Die FW-Summe 165+16 = 181 zeigt die 10 Maßeinheiten in der DR, denen, wie oben dargelegt, das Kreisflächenverhältnis 1:3 entspricht.
2. Durch Abzug von je einem Zähler für das unsichtbare A ergibt sich die ZS 325 und die FS 224, zusammen 549 = 9*61. In den Einzelziffern der Faktorenfolge 61*9 erkennt man die oben behandelte Zahl 619.
Den nunmehr 25 Buchstaben der Kreuzesinschrift entspricht die Summe 325 = 25*13 der Zahlen 1-25. Man kann sie so in ein Quadrat eintragen, daß die horizontalen, vertikalen und diagonalen Summen jeweils 5*13 = 65 betragen:
|
|
|
Eine Interpretation dieses "magischen" Quadrats findet sich in einem früheren Beitrag.
3. Ein Quadrat entsteht durch Winkelverschiebung eines Achsenkreuzes. Im Fall der Kreuzesinschrift geschieht dies so, daß die ZS+FS von je zwei Achsenarmen zusammenstimmen:
|
|
ZS |
FS |
sm |
|
ZS |
FS |
sm |
GS |
|
IESUSN |
83 |
49 |
132 |
ZARENUS |
97 |
76 |
173 |
305 |
|
REXIUDA |
77 |
52 |
129 |
EORUM |
68 |
47 |
115 |
244 |
|
|
160 |
101 |
261 |
|
165 |
123 |
288 |
549 |
|
261:288 = 9*(29:32); 305:244 = 61*(5:4); 132:129 = 3*(43:44) |
||||||||
Für ein passendes Rechteck sind zwei Änderungen vorzunehmen: Das A wandert zu IESUSN und das R tritt zu ZARENUS als rechter oberer Eckpunkt. Auf diese Weise kommen oben und unten 8+7 Buchstaben und links und rechts je 5 Buchstaben zustande, die den Elementen des DR-Rahmens bzw. den 10 Punkten der Tetraktys zugeordnet werden können:
|
|
Die einander gegenüberstehenden Seiten bilden mehrere Zahlenverhältnisse:
·
|
|
ZS |
FS |
sm |
|
ZARENUSR |
114 |
93 |
207 |
|
IESUSNA |
84 |
50 |
134 |
|
|
198 |
143 |
341 |
|
143:198 = 11*(13:18) = 11*31 > 42 |
|||
|
114:84 = 6*(19:14); 93:114
= 3*(31:38) |
|||
Die Anfangs-, Mitte- und Endbuchstaben ZENR-IVA haben die ZS 88, das ZS-Verhältnis zu den übrigen 8 Buchstaben beträgt 88:110 = 22*(4:5).
· Auch für die linken und
rechten Buchstaben liefern die 6 Anfangs-,
Mitte- und Endbuchstaben ein Zahlenverhältnis
zu den 4 übrigen Buchstaben:
|
|
ZS |
FS |
sm |
|
ERM-EID |
52 |
44 |
96 |
|
OV-XV |
75 |
37 |
112 |
|
|
127 |
81 |
208 |
|
96:112 =
16*(6:7) = 208 = 16*13 > 21 |
|||
|
44:52 = 4*(11:13) |
|||
Der ZS 52 und FS 44 entsprechen zwei geometrische Figuren, aus denen ein Oktaeder zusammengesetzt werden kann. Die FW 42 und 21 weisen auf drei DR von je 21 Elementen hin.
Von Interesse sind die angrenzenden Zahlen 37 und 38. 38 ist die Differenz zwischen der FS 37 und der ZS 75. Aus den ZS 38 und 37 baut sich die ZS 303 des SATOR-Quadrats auf.
Die ZS+FS 112 = 16*7 ist eine bedeutende Kennzahl für das Dezimalsystem. Der Faktor 7 enthält, wie oben dargelegt, einen unsichtbaren Mittelpunkt. Die Einzelziffern geben das Kreisflächenverhältnis 1:3 wieder.
·
Die ZS+FS verbinden durch die Umkehrfaktoren 31
und 13 die zwei Gruppen von 15
und 10 Buchstaben miteinander.
·
Eine Beziehung zwischen 15 und 10
Buchstaben zeigt sich auch darin, daß die Differenzsumme 101 zwischen der FS 224 und
ZS 325 sich aufteilt in 55+46 für die ZS und die FS der Zahlen 1-10.
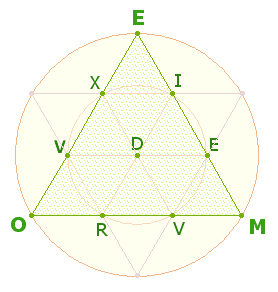
4. Die Buchstaben der linken und rechten Seite lassen sich auf den 10 Tetraktyspunkten anordnen:
|
|
Die ZS+FS der drei Eckpunkte 31+21 = 52 enthält in zweistelliger Zusammensetzung die zwei Kreisflächenverhältnisse 3:1 und 2:1. Die Buchstabenkombination MEO bedeutet für das Meinige. Die ZS+FS der 7 übrigen Punkte beträgt 96+60 = 12*(8:5) = 156 = 12*13. Die Umkehrung der Kreisflächenzahlen zeigt die Bewegung von innen nach außen und von außen nach innen.
5. Die Gruppe von 7+8 Buchstaben läßt
sich auf den Punkten und Linien des DR-Rahmens oder aufgeteilt in einem DR-Kreuz eintragen:
|
|
Die Zusammengehörigkeit von
zwei Buchstabengruppen Buchstaben entspricht hier der natürlichen numerischen
Symmetrie der Ausgangsabfolge, d.h., 3+4 Buchstaben von IES-USNA und 4+4 von ZARE-NUSR gehören auch im DR-Kreuz zusammen. Die
Linienbuchstaben sind mäandrisch angeordnet. Die beiden Buchstabengruppen haben
folgende ZS+FS:
|
|
ZS |
FS |
sm |
|
IES-ZARE |
78 |
65 |
143 |
|
USNA-NUSR |
120 |
78 |
198 |
|
|
198 |
143 |
341 |
|
65:78 = 13*(5:6) |
|||
|
143:198 = 11*(13:18) |
|||
Die zweifache Verhältnis 143:198 ergibt sich
daraus, daß die ZS der
ersten Gruppe die FS der
zweiten Gruppe ist. Die Einzelziffern der Zahl 78 weist auf die Elemente des DR-Rahmens hin, die Faktoren 3*26 auf drei Oktaeder, die jeweils aus 26 Elementen bestehen. Dies tritt auch in der vollständigen ZS 326 der Kreuzesinschrift in
Erscheinung.
Die
Differenzsummen zwischen FS
und ZS sind 13 und 42. Es handelt sich um eine Umkehranalogie: 4 Linien des DR-Durchmessers
bedeuten 3
Flächeneinheiten, 2 hexagonale Linien 1 Flächeneinheit.
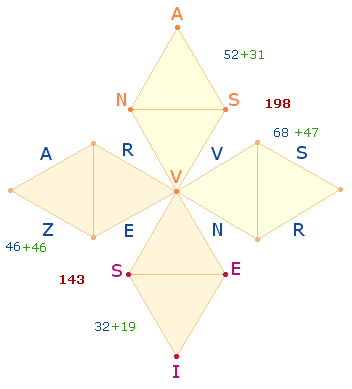
6. Die mäandrische
Anordnung der Linienbuchstaben führt zu einem weiteren Verhältnis 143:198, indem die ZS+FS der 2+4 Buchstaben der linken Seite 143 beträgt und die übrigen 3+6
Buchstaben 198:
|
|
ZS |
FS |
sm |
|
SN-ARUS |
87 |
56 |
143 |
|
AVI-ES-ZENR |
111 |
87 |
198 |
|
|
198 |
143 |
341 |
Bei dieser Kombination der
zwei Buchstabengruppen kehrt sich die ZS
78 zu 87 um
und entsprechend 65 zu 56. 87 = 3*29 weist auf die Rahmenelemente von drei DR-Kreuze hin.
7. Die Zahlen 143
und 198 sind näher zu erklären:
·
Die Faktoren 11*13 sind auf die Elemente der Raute und des
sanduhrförmigen Doppeldreiecks zu beziehen, die in der DR ineinandergreifen:
|
|
Da die Raute den hexagonalen und den Erweiterungsbereich
umfaßt, steht sie für 3 Kreisflächeneinheiten, das
Doppeldreieck für 1 Flächeneinheit. Beide
Figuren zusammen bestehen aus 17 Elementen, davon 3 Flächenelemente. Aus der Trennung dieser drei Elemente von
den übrigen Elementen ergibt sich in zusammengesetzter Form die Zahl 143:
|
|
·
Die Faktoren 11*18 stellen als Summanden die Numerierungssumme der
Elemente der hexagonalen Achse und ihrer Hexagrammerweiterung dar, wenn sie vom
Mittelpunkt ab von 1 bis 5 bezeichnet werden:
|
|
·
Das Verhältnis 13:18 entsteht
numerisch aus der FS und der ZS der
Zahlen 10+8 = FS
7+6. Die Zahlen 10 und 8 sind als Komplementärzahlen von 1 und 3 und somit als
Kennungszahlen des einen Gottes in drei Personen zu betrachten. Geometrisch
stellt 13:18 die Elemente der drei
hexagonalen Kreisachsen und des Tetraktysrahmens das Kreisflächenverhältnis 1:3 dar:
|
|
·
Die Zahlen 10+8 können auch auf die 10 Linien
der DR bezogen werden, indem sie aufgeteilt
werden können in (2+8)+8. Wie in obiger
Grafik gezeigt wurde, sind 2 Querlinien
1 Flächeneinheit und 8 Rahmenlinien 3 Flächeneinheiten gleichzusetzen.
·
Die Zahl 198
bewirkt die Umkehrung der Zahl 143 zu 341. Die
Zahl 1
ist als unsichtbarer Mittelpunkt zweier zusammengeschlossener Rauten zu
verstehen: aus 2*4 Punkten werden sichtbare 7 Punkte. Das ist auch der Sinn der Zahl 791,
der FS der 6 Umkehrungen von 143:
|
Zahl |
134 |
143 |
314 |
341 |
413 |
431 |
1776 |
|
FW |
69 |
24 |
159 |
42 |
66 |
431 |
791 |
|
791
= 113*7 |
|||||||
In der Zahl 113 wurde bereits oben ein
unsichtbarer Mittelpunkt entdeckt: 1+13 =
(1+13)+13 = (7+7)+13. Dem Additionsergebnis entsprechen
(1+3)+3 = 7
Flächeneinheiten.
8. Die Werte der drei
Oktaederebenen sind:
|
|
o. |
Mi. |
u. |
|
|
ZS |
69 |
54 |
75 |
198 |
|
FS |
56 |
34 |
53 |
143 |
|
|
125 |
88 |
128 |
341 |
Zwei Hälften und das Ganze ergeben:
|
|
o. |
u. |
G. |
sm |
FW |
|
ZS+FS |
213 |
216 |
341 |
770 |
25 |
|
FW |
74 |
15 |
42 |
131 |
131 |
|
sm |
156 = 12*13 |
156 |
|||
Die Einzelziffern der
Faktoren 12*13 geben die beiden Kreisflächenverhältnisse wieder.
Erstellt: Mai 2017