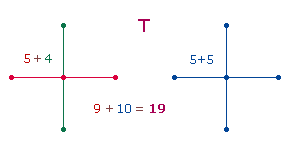DAS SATOR/ROTAS-QUADRAT
STRUKTURELLE
GESICHTSPUNKTE
I. Zwei Achsenfiguren
II. Die Buchstaben des äußeren
Quadratrahmens
III. Das innere Quadrat
b) aus den Numerierungen 23+24 der Doppelraute
IV. Numerierungen der DR-Punkte
VII. Strukturelle und gematrische Folgerungen
Die folgenden Ausführungen behandeln einen speziellen
Aspekt der Struktur: die Bedeutung des Achsenkreuzes und des Doppelrautenkreuzes für die Bildung der 25 Buchstaben.
Struktur bedeutet gleichzeitig Zahl und Zahl Buchstabe.
Daher gehen Struktur und Zahlenwerte
des SATOR-Quadrats
(SQ) Hand in Hand.
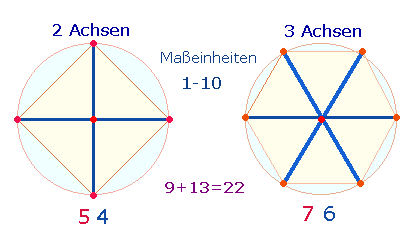
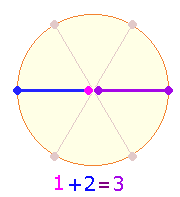
I. Zwei Achsenfiguren
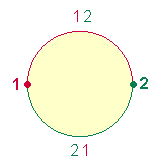
1.
Ausgangspunkt
struktureller Elemente für das SATOR-Quadrat sind zwei
geometrische Figuren aus 2 und 3 Achsen. Ihre 10
Radialmaße sind als konstitutiv für das Dezimalsystem anzusehen:
|
|
Das rechtwinklige Achsenkreuz entwickelt sich durch
Winkelverschiebung zum Quadrat, die hexagonalen Achsen zum Tetraktysstern und durch ein Achsenkreuz zweier Doppelrauten (DR) zum Oktaeder.
Während das Hexagon zu einem dreidimensionalen Abschluß kommt, können
Achsenkreuze und Quadrate sich unendlich weit ausdehnen.
Die Zahl von 13 und 9 Elementen kann dreistellig zu
139 zusammengesetzt werden. Bemerkenswert ist, daß bei Numerierung zweier DR
von 1-23 und 1-24 zwei Summen zustande kommen können, 2*139 = 278 und 3*139
= 417. Darauf wird weiter unten
eingegangen.
Die analoge Entwicklung beider
Achsenkreuze zu Flächenfiguren habe ich unter Zahl 29 in der Untersuchung über das Carmen
Saeculare des Horaz dargelegt.
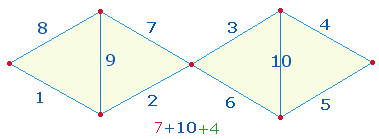
10 Maßeinheiten enthält auch die DR:
|
|
2.
Die
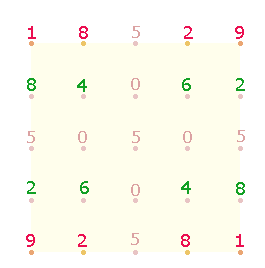
5*5 Buchstaben des SATOR-Quadrats (SQ)
sind nach ihrem Konstruktionsprinzip auf Punkten angeordnet. Das 5*5-Punkte
Quadrat (25PQ) läßt sich durch Winkelverschiebung eines Achsenkreuzes
AK5 bilden, d.h. jeder Achsenarm besteht aus 5
Punkten:
|
|
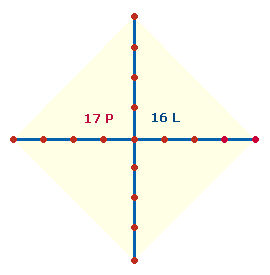
Jeweils 5 Punkte eines Achsenarms
begrenzen 4 Maßeinheiten. Letztere können als Zählelement entweder
einbezogen oder ausgespart sein. Die Gesamtzahl der Elemente ist somit (bei
einem Mittelpunkt) entweder 33 (=17+16) oder 17 (=9+8). Die Zahl 17 wiederum ist die Gesamtzahl der Elemente des nächst
niedrigeren Achsenkreuzes AK3.
4.
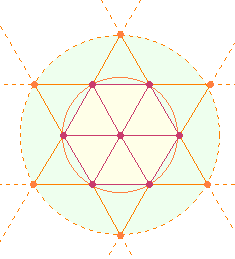
Das 5*5-Punkte Quadrat hat einige grundlegende
Eigenschaften mit dem Tetraktysstern gemeinsam:
– Das 25PQ besteht aus zwei konzentrischen Quadraten,
den Tetrakysstern umspannt ein konzentrischer zweiter Kreis:
|
|
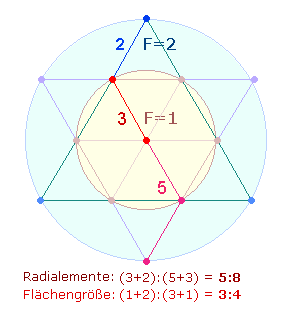
–
5 Reihen von Punkten sind den 5 Durchmesserelementen des
Kreises vergleichbar: Der Mittelpunkt gilt als Begrenzung für jedes Radialmaß, ist
also zweimal zu denken. Insofern ein Radialmaß von zwei Punkten begrenzt wird,
kann man von 2*3
Radialelementen des Kreises sprechen:
|
|
–
Die konzentrische Erweiterung beider Figuren
vermehrt die Radialelemente jeder Seite um 2. Auf diese Weise erhält man
als konstitutiv für das Dezimalsystem 5+5 = 10 Radialelemente:
|
|
–
Die Mittelpunktszahl von 25 ist 13. Aus 13 Punkten besteht der
Tetraktysstern. Die Summe beider Zahlen (1-25, 1-13) ist durch 13 teilbar: 325 = 25*13,
91 =
7*13. Die Einzelziffern geben
die doppelten Radialelemente in der Gleichungsform 3+2 = 5
wieder.
Der Faktorenwert (FW) von 25 ist 10, was die Zahl 25 und die Summe 35 besonders relevant für das
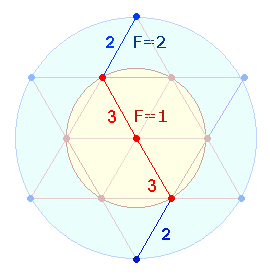
Dezimalsystem macht. Bedeutsam in diesem Zusammenhang sind die 7 Punkte der Doppelraute (DR), die sich bei der Erweiterung
des Hexagons zum Tetraktysstern bildet: 2 Punkte gehören zur Erweiterung 5 zum hexagonalen Teil. Somit
bedeutet eine Null nach einer Zahl immer 2*5.
4.
Ein wesentliches strukturelles Ergebnis des vollendeteten
Tetraktyssterns besteht darin, daß jedes hexagonale Dreieck spiegelsymmetrisch
nach außen projiziert ist. Den 7 Elementen eines Dreiecks werden durch ein Umkehrdreieck 4 Elemente hinzugefügt. Damit
kommt den Zahlen 4
und 7 eine besondere Bedeutung
zu:
|
|
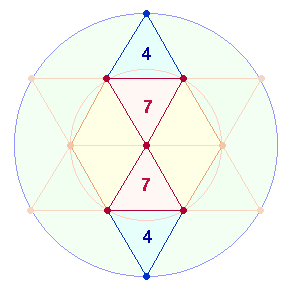
Dieses Ausfaltungsprinzip
gilt auch für das Quadrat. Denn die Verbindungslinien zwischen den
Kreislinienpunkten des Achsenkreuzes schaffen ein Rautenquadrat aus 4 gleichschenklig-rechtwinkligen
Dreiecken:
|
|
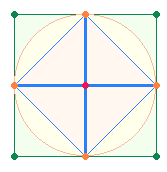
Durch Einziehung von
Diagonalen (im erweiterten Rautenquadrat) erhält man im vollendeten 25PQ eine Doppelrautenstruktur
ähnlich wie im SQ:
|
|
Zu den Buchstaben eines
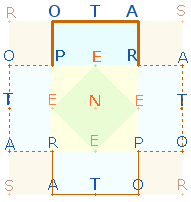
kleinen Rautenquadrats siehe den Beitrag PERNET.
Im Folgenden werden die
Buchstaben des äußeren und inneren Quadratrahmens aus der Zahl von
Konstruktionselementen erklärt, zuerst nach dem Ausfaltungsprinzip, dann nach
dem Prinzip der Winkelverschiebung, schließlich aus zwei Numerierungen der
Doppelraute. Die Erklärungen konvergieren mit anderen strukturellen und
inhaltlichen Modellen.
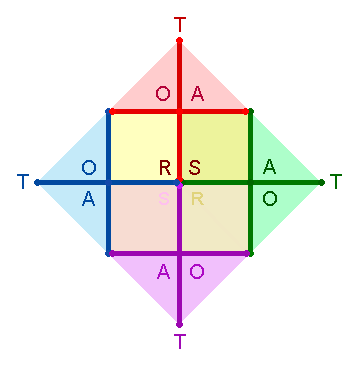
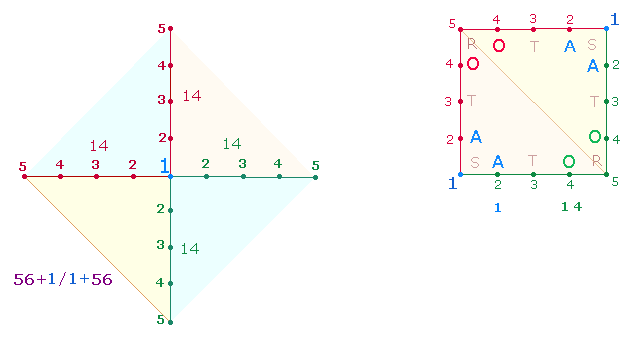
II. Die Buchstaben des äußeren Quadratrahmens
1.
Das SATOR-Quadrat zeigt als Grundgerüst 1 großes und 4 kleine Achsenkreuze (blau, rot, grün, violett). Durch Ausfaltung der 4 Winkel entstehen das 25PQ und die entsprechenden
Zahlenwerte für die Buchstaben der SQ-Rahmens:
|
|
|
Numeriert man die 5
Punkte eines kleinen Achsenkreuzes, dann steht im Mittelpunkt die 1
und die übrigen 4 Punkte werden mit den Zahlen 2-5
bezeichnet. Die Addition 2+3+4+5 ergibt 14. Das A ist der 1., das O der 14. Buchstabe. Also sind jedem
kleinen Achsenkreuz diese beiden Buchstaben zugeordnet:
|
|
Unterstützt wird der Umkehrcharakter von
OA/AO durch zwei unterschiedliche Zuordnungen der
Durchmesser- und Radialelemente der 3 Hexagonalachsen, wobei 4+7 und 3+8 als zweistellige Zahlen
behandelt werden.
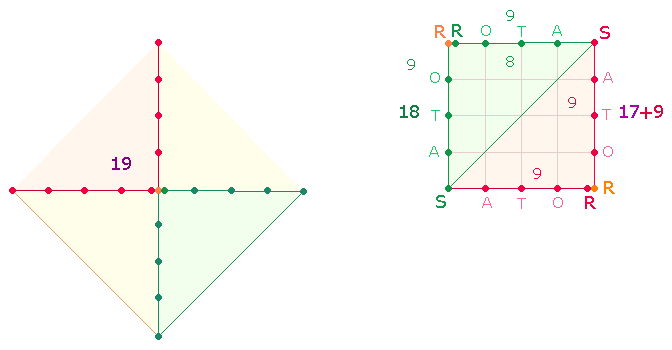
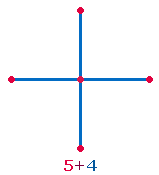
2. Das viermalige
T
entsteht durch doppelte Zählung aus den 5 Punkten
+ 4 Linien des einfachen
Achsenkreuzes. Da jede Achse aus 3P + 2L besteht, lautet die Rechnung (5+4)+(5+5) = 19,
der Zahlenwert für das T:
|
|
Dasselbe Ergebnis erhält man
durch Doppelzählung der jeweils 5 Achsenpunkte des 5*5 Punktequadrats, worauf die
Zahlensumme (ZS)
109 des TENET-Kreuzes (in Einfachzählung)
hinweist.
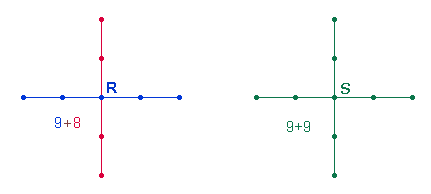
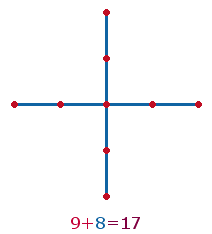
3.
Das große Achsenkreuz besteht aus 9 Punkten + 8 Linien bzw. 9+8 Durchmesserelementen
(DM-E). Der Zahl 9+8=17 entspricht der Buchstabe R. Jede Achse aber besteht
aus 5 Punkten und 4 Linien. Verdoppelt man
beide Zahlen erhält man den Buchstaben S, der die 18. Stelle im Alphabet einnimmt:
|
|
Die 4 Seiten des
Quadratrahmens mit jeweils 5P + 4L entstehen nun dadurch, daß – entsprechend der Konstruktion des
Tetraktyssterns – die 4 Winkel vom Mittelpunkt aus jeweils um ihre zwei äußeren Punkte
spiegelbildlich nach außen projiziert werden.
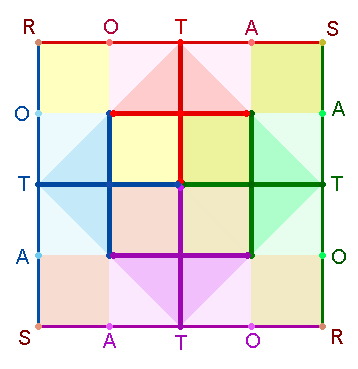
1.
Die zweite Erklärung der Buchstaben A und O geht von der Numerierung
der Punkte des AK5
und der Winkelverschiebung aus:
|
|
2. Die Buchstaben
R S
T des SQ-Rahmens mit den Zahlenwerten (ZW) 17 18 19 lassen sich aus der Punktezahl des AK5 ableiten: Jede Achse
besteht aus 9
Punkten, zusammen 18.
Um die Zahl von 17 Punkten bei 1 Mittelpunkt auszugleichen, bedarf es
eines weiteren Achsenkreuzes 19 Punkten mit 3 Mittelpunkten, das durch
Winkelverschiebung – von unten rechts nach oben links – die anderen beiden
Zahlen bewirkt, wobei die Linien mitzuzählen sind. Je zwei Mittelpunkte sorgen
für die Zahl 18 = S (9+9), während die rechte obere und linke untere
Ecke mit einem Mittelpunkt die Zahl 17 = R
bildet:
|
|
Das S
verläuft von links unten nach rechts oben mit 9+9 Elementen bis
zum zweiten S, das dieselbe Bewegung
in die Gegenrichtung vollzieht. Das R
setzt oben links ein und durchläuft über einen einzigen Eckpunkt nach rechts
unten 17 Elemente.
18
Elemente bedeuten 5+5 Punkte, 17 Elemente 4+5
Punkte.
3.
Diese
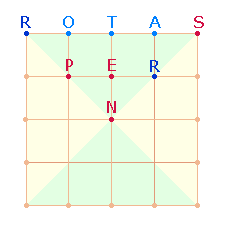
Struktur des Quadratrahmens hat drei Folgen für ROTAS:
Das Wort ROTA kann sich auf ein Substantiv und ein Verb beziehen:
Als Substantiv ist ROTAS Akk.Pl. die
Räder, als Verb 2.Ps.Sg. von ROTARE – du
drehst; hinzukommt der Imperativ ROTA
– drehe. Aus dieser Mehrdeutigkeit läßt sich – von unten
links beginnend – zunächst der Satz bilden:
SATOR ROTAS – Schöpfer, Du
drehst.
Von oben links lassen sich drei Wörter bilden:
ROTA SATOR ROTAS
– Drehe, Schöpfer, die Räder.
Den ganzen Vorgang kann man von der
oberen rechten Ecke wiederholen.
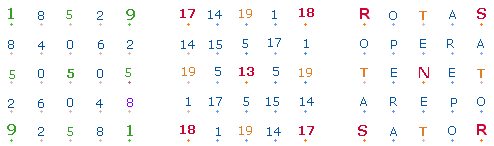
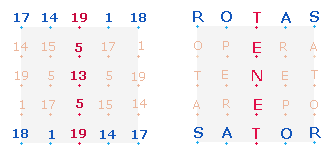
Die Zahlensummen (ZS) der 10+14 Buchstaben sind 138+189 = 327 = 3*109.
Zwei gegenüberliegende Quadratseiten werden durch TENET verbunden:
SATOR TENET ROTAS – Der Schöpfer hält die Räder.
4.
Die
drei Innenbuchstaben des Quadratrahmens ATO haben die ZS 34. Die Aufteilung 35+34 = 69
ist durch das AK5 erklärbar, wenn man den Symmetrieelementen 16+16 = 32 einmal 3 und einmal 2 Mittelpunkte zuordnet.
Auch in der DR ist die Aufteilung 35+34
vorhanden, und zwar durch 3 geometrischen Figuren aus 11,
13 und 17 Elementen:
|
|
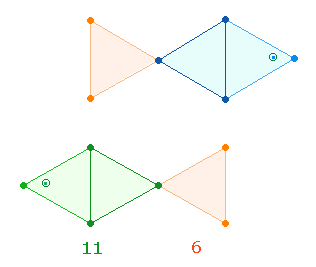
Die Konstellation der ersten Grafik ergibt 35
Elemente, die Verdoppelung der Fischfigur 34 Elemente.
Multipliziert man die Werte der 3 Innenelemente und
aller 5 Punkte, erhält man mit 136 und 276 die ZS der Zahlen 1-16 und 1-23.
Deren FS sind die Umkehrzahlen 102 und 201, die zusammen die ZS der 25
Buchstaben bilden.
a) nach dem Achsenkreuzmodell
1.
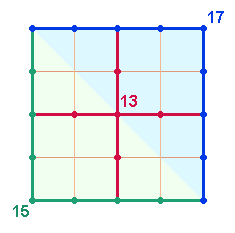
Zwei Ecken des Quadratrahmens mit zwei Punkten zu
belegen, ist darin sinnvoll, daß der Quadratrahmen diagonal (links oben nach
rechts unten) in 2*17 Elemente geteilt wird. Geht man aber von nur einem Punkt aus, sind die
insgesamt 32
Elemente so zu teilen, daß eine Diagonalhälfte zwei Eckpunkte besetzt und so
die beiden Hälften durch 17 und 15 Elemente definiert sind. Vom Achsenkreuz, das aus ebenfalls 17 Elementen besteht, bleiben
nach Abzug von 4
Rahmenpunkten 13 Elemente übrig.
|
|
Die Summe der drei Zahlen 17+15+13 ist 45. Rechnet man für jede
Diagonalhälfte und für das Achsenkreuz jeweils 17 Elemente, ergibt sich das Verhältnis 3*(15:17) = 3*32 = 96.
2.
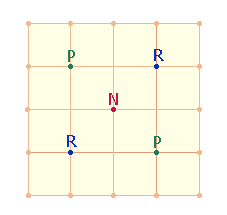
Den Zahlen 17 15 13 lassen sich die Buchstaben R P N im inneren Quadrat zuordnen; sie bilden ein Dreiecksmuster:
|
|
Verlängert man das Dreiecksmuster zu den Eckpunkten
des Quadratrahmens, läßt sich das gesamte Quadrat in 4
zum Mittelpunkt zulaufende Dreiecke zu je 9 Buchstaben einteilen. 5
dieser Buchstaben: die Buchstabengruppe OTA sowie 2 R
ergeben die ZS 4*17, die restlichen 4 Buchstaben SPEN
die ZS 3*17:
|
|
3.
Läßt man das zweite R weg, ergeben je 4 Buchstaben die Zahlensumme (ZS) 3*17 = 51, zusammen 102. Fügt man die Buchstaben sinnvoll zusammen,
erhält man das Wort PENS-ATOR. – der Abwiegende, der im Gleichgewicht Haltende. Dieses Wort enthält die 8 verschiedenen Buchstaben
des Quadrats. Die ZS
der übrigen Buchstaben ist 201.
Nun entspricht die ZS 102 der Faktorensumme (FS) der Zahlen 1-16 und der ZS 201 der FS der Zahlen 1-23.
4.
Die ZS 102 und 201 legen die Vermutung nahe, daß Faktorensummen ein entscheidendes
Konstruktionsprinzip des SQ darstellen. Sie betreffen insbesondere 16 Maßeinheiten und 17 Punkte des Achsenkreuzes AK5:
|
|
Das FS:ZS-Verhältnis der Zahlen 1-16 beträgt 17*(6:8) = 34*(3:4) und entspricht damit der Zusammensetzung
der Zahl 16
selbst aus der Summe der Zahlen 1-3 und 1-4. Im Gefolge dieses Verhältnisses rückt die Primzahl
17 um 17+17 weiter, sodaß das FS:ZS-Verhältnis der Zahlen 1-17 17*(7:9) beträgt und die FS+ZS der Zahl 16
und 17 jeweils zusammengenommen das Verhältnis 17*(14:16) = 34*(7:8)
= 510 bilden.
Dieselbe FS+ZS 510 kommt für die Zahl 24 zustande durch 210+300 = 30*(7:10). Wenn
man die Zahlen 7 und 10
auf die Punkte des Hexagon und der Tetraktys bezieht, bedeutet die Zahl 24 12+12 Linien
bzw. Maßeinheiten des Tetraktyssterns.
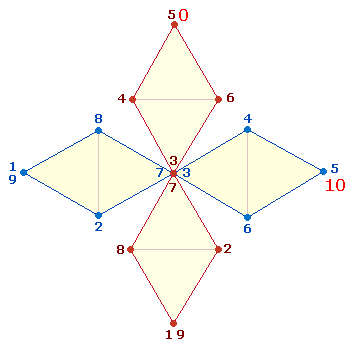
b) nach zwei Numerierungen der Doppelraute
1.
Das
Verhältnis 7:8 ist
auf die Punkte und Linien des DR-Rahmens beziehbar. Darauf haben die Zahlen 16
und 17 nur Platz, wenn diese 15
Elemente schleifenförmig numeriert werden. Dies dürfte ein wichtiger Grund für
das P und R des inneren Quadratrahmens des SQ
sein.
Der DR-Rahmen umschließt 2*3 Binnenelemente,
jeweils 2
Dreiecke, die durch 1 Querlinie getrennt sind. Durch schleifenförmige Umfahrung
wird die Numerierungszahl von 21 DR-Elementen auf 23 Positionen erhöht.
Da ein DR-Kreuz durch
Zusammenlegung der Endpunkte zu einem Oktaeder zusammengefügt werden kann, läßt sich die Numerierung
nach der Zahl 17 auf der gegenüberliegenden Position mit der Nummer 18
fortsetzen, sodaß die Endzahl der Numerierung 24 beträgt. Auf diese
Weise entsteht eine gegenläufige Numerierung der Binnenelemente, die durch die
Umkehrung der FS 201 und 210 der Zahlen 23 und 24
gestützt wird:
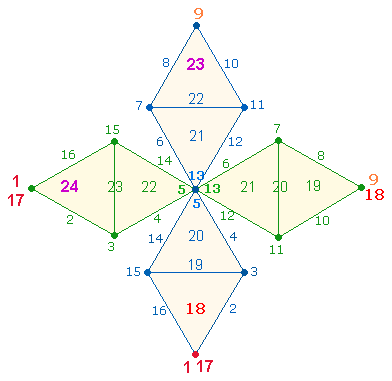
Die FS
102 = 17*6 der Zahlen 1-16
= begründet die Numerierung 17+6, die FS
119 = 17*7 der Zahlen 1-17 die Numerierung 17+(1+6).
Die ZS+FS
153+119
der Zahlen 1-17 haben die FW 23+24,
enthalten also beide Numerierungen in sich.
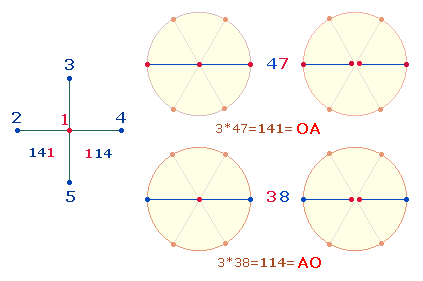
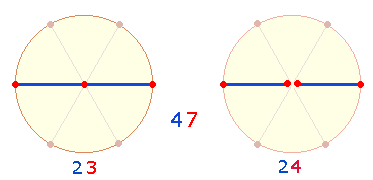
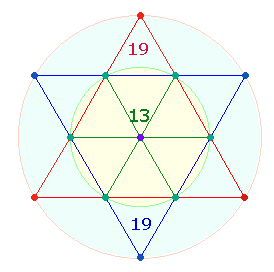
2. Die 47
Numerierungspositionen dieses DR-Kreuzes haben ihre Parallele im Verhältnis 4:7
der Zahlen 12:21 und im Doppelaspekt von 5 DM-
und 6 Radialelementen des Kreises:
|
|
Die Rechnung für drei Achsen ist 3*11 = 33, dasselbe Ergebnis wie die Addition 16+17. Fügt man den FW 14
zu 33 hinzu, erhält man 47.
Auch im SQ ist ein Ergebnis
mit diesen beiden Zahlen zu finden: Die ZS+FS
der 25 Buchstaben beträgt 303+249
= 552 = 23*24.
Die Bedeutung der Zahl 47 zeigt
sich im ZW 47 der Wörter DEVS – Gott und IVS –
Recht. IVS hat mit den
beiden DR-Numerierungen die Gemeinsamkeit, daß die FS
der drei Buchstaben 23 und die Differenz 24 beträgt.
3.
Die
Zahlen des Doppelrautenrahmens ergänzen sich horizontal paarweise zu 18
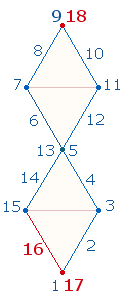
und in zwei DR zu 36. Dies ist bei der Numerieung des obersten Punktes (9, 9 18)
nur dann der Fall, wenn man beide Numerierungsweisen vornimmt. Das
Summenverhältnis der 35 Rahmenelemente zu den 12 Innenelementen
beträgt 324:252 = 36*(9:7).
Die ZS der Zahlen 1-23
+ 1-24 sind 276+300 = 576, die FS
201+210 = 411, beide zusammen
ergeben 987. Die Ziffern 987 sind nicht nur
symmetrische Entsprechungen zu 123, sondern die dreistellige Zahl 987
läßt sich in das Produkt 21*47 aufteilen und verweist damit sowohl auf die 21
Elemente der Doppelraute als auch auf die Bedeutung der beiden Summanden 23+24.
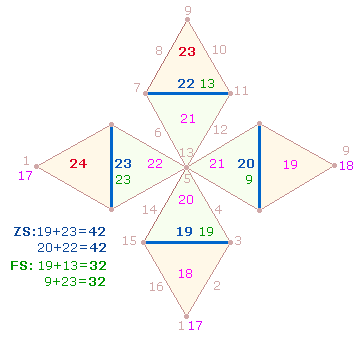
4. Die gegenläufige Numerierung der
Mittelelemente bewirkt, daß je zwei parallele Zahlen sich zu 42 ergänzen (z.B. 18+24). Eine Gemeinsamkeit
der beiden Numerierungen ist, daß die FS der beiden
Querlinienzahlen jeder Numerierung (19+22, 20+23) jeweils 32 beträgt (19+13, 9+23). Verwandelt
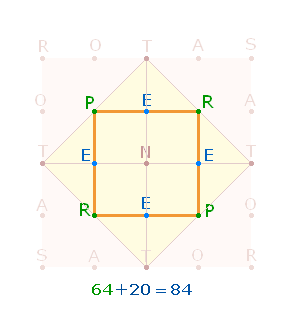
man die 4 inneren gleichseitigen Dreiecke des DR-Kreuzes in
gleichschenklig-rechtwinklige Dreiecke, fügen sich die 4 Querlinien zu einem
Quadrat zusammen, das von einem Rautenquadrat umgeben wird:
|
|
|
Die Eckpunkte des inneren Quadrats sind
zweimal durch P+R
mit den Zahlenwerten 15+17 =
32 besetzt, die 4 Mittelpunkte der Seitenlängen durch E
mit dem ZW 5. Die vier Eckbuchstaben mit der ZS 64
entsprechen also der FS der 4 Querlinien des DR-Kreuzes und die 4 E mit dem ZS 20
der Differenz zur ZS 84. Dieses interne FS:ZS-Verhältnis 64:20 wird zum externen Verhältnis 64:84, wenn man die ZS 32+5 = 37 einer Quadratseite viermal zählt: 64+84 = 4*37 = 148. Die Zahl 37
weist auf die 3+7 Punkte oder die 37 Elemente der Tetraktys
hin. In einem DR-Kreuz sind zweimal zwei Tetraktys eingebunden, da der
Tetraktys ein Dreieck der DR fehlt, die sich somit über zwei Tetraktys erstreckt.
Die Einzelziffern der Zahl 148 kennzeichnen die Elemente eines Quadrats: 1 Fläche, 4 Linien und 4*2 Begrenzungslinien. In der Aufteilung 1+48 ist die Zahl auf den Mittelpunkt und 48 Elemente des Tetraktyssterns beziehbar.
Nimmt man noch die 8 Begrenzungspunkte der 4 Querlinien hinzu,
ergibt sich folgende ZS+FS:
|
|
ZS |
FS |
sm |
|
QL |
84 |
64 |
148 |
|
P |
72 |
58 |
130 |
|
|
156 |
122 |
278 |
Dieses Ergebnis ist in Catulls carmen 85 zweifelsfrei nachweisbar. Dort haben die gleiche ZS+FS die Wörter FACIAM FIERI SENTIO:
|
|
ZS |
FS |
|
|
FACIAM |
32 |
23 |
55 |
|
FIERI |
46 |
39 |
85 |
|
SENTIO |
78 |
60 |
138 |
|
|
156 |
122 |
278 |
Durch 139 ebenfalls teilbar ist die ZS+FS der 12
Binnenelemente von 18-23 und 19-24: 252+165 = 417 = 3*139.
5. Die bereits erwähnte Durchdringung des SQ von ZS und FS
zeigt sich in den drei Mittelzeilen besonders: Deren ZS 165 (52-61-52) ist die FS (82+83) der
Mittelelemente der beiden Numerierungen. Die ZS der 5
Buchstaben des inneren Rautenquadrats beträgt 33, die der umgebenden
5+5 Buchstaben jeweils die doppelte Summe 66:

165
ist die FS der Zahlen 1-21 = 231 = 21*11. Darin eingegliedert ist 64 als FS der Zahlen 1-12.
Die Differenz von 66 zur ZS 231 wird
zweimal durch die Buchstaben SAO von SATOR/ROTAS zustandegebracht, sodaß 21
Buchstaben den durchschnittlichen ZW 11
haben. Es bleiben übrig zweimal die Primzahlen 17 und 19
für die Buchstaben RT. Deren doppelte ZS+FS ist 4*36
= 144 = 6*24. Da
die ZS+FS
des gesamten Buchstabenquadrats 23*24 beträgt, ist das ZS+FS-Verhältnis der 21:4
Buchstaben 24*(17:6).
Die 15+6
Buchstaben bilden das ZS+FS-Verhältnis 3:1:
|
|
ZS |
FS |
sm |
|
15 Bu. |
165 |
141 |
306 |
|
6 Bu. |
66 |
36 |
102 |
|
sm |
231 |
207 |
408 |
Die Konstitutivzahlen 82+83 ergeben sich als FS auch aus der Einteilung
der Zahlen 1-21 in Primzahlen und zusammengesetzten Zahlen, wobei die
Zahl 4 hier den Primzahlen zugeteilt ist, da der FW
derselbe ist:
|
|
|
ZS |
FS |
GS |
|
10 PZ |
1 2 3 4 5
7 11 13 17 19 |
82 |
82 |
164 |
|
11 zsg.Z. |
6 8 9 10 12 14 15 18 20 21 |
149 |
83 |
232 |
|
|
Differenz:
231-165 = 66 |
231 |
165 |
396 |
Bei Berechnung der Zahlenreihen 1-23
und 1-24 sind die vorhergehenden Summen zu verdoppeln und die
über 21 liegenden Zahlen hinzuzufügen:
|
|
|
ZS |
2*ZS |
GS |
FS |
2*FS |
GS |
GS |
|
22 PZ |
23 23 |
46 |
164 |
210 |
46 |
164 |
210 |
420 |
|
25 zsg.Z. |
22 22 24 |
68 |
298 |
366 |
35 |
166 |
201 |
567 |
|
|
|
114 |
462 |
576 |
81 |
330 |
411 |
987 |
|
Differenz: 576-411 = 165 |
||||||||
Unter Hinzufügung der Zahl 4 zu
den Primzahlen ergibt sich die FS 210 der Zahlen 1-24 und für die
zusammengesetzten Zahlen die FS 201 der Zahlen 1-23. Die Zahlen 22 und 25
sind auf die beiden oben eingeführten Achsenfiguren zu beziehen. Die Punktezahl
12 erweitert sich um 3, wenn für jede Achse der
Mittelpunkt gezählt wird. Verlegt man 4 zu den zusammengesetzten
Zahlen, bedeuten 20 Primzahlen 10+10 Maßeinheiten und 27
zusammengesetzte Zahlen 12+15 Achsenpunkte. Die Differenz 165 der beiden
Zahlenreihen 1-23 und 1-24 ist die FS der Zahlen 1-21:
Zur Differenz 2*66 kommt noch die Differenz 68-35 = 33
hinzu. Diese Aufteilung der ZS 66+33+66 der drei Mittelzeilen wurde oben schon eingeführt,
erhält hier aber eine tiefere Begründung.
Dem Doppelaspekt von 20+27 der beiden Achsenfiguren entsprechen 40
Maßeinheiten und 43 Punkte zweier DR-Kreuze. Es ergibt sich so das Gesamtverhältnis von 60:70 oder 63:67.
6. Nachdem eine Begründung für die
gematrische Dreiteilung der drei Mittelzeilen gefunden wurde, bietet sich als ein
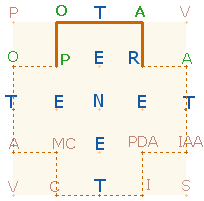
sinnvolles Wort für die ZS 66 PORTA an:
|
|
|
Im 6. Buch der Fasten, Vers 192, hat
Ovid durch das Wort PORTA und der ZS 303 die Beziehung zum SATOR-Quadrat bezeugt.
Das Distichon lautet:
191 Lux eadem Marti festa est, quem prospicit extra
192 ADPOSITUM TECTAE PORTA CAPENA VIAE:
Derselbe Tag ist auch dem Mars geweiht, auf
(dessen Tempel),
der neben der
befestigten Straße gelegen ist, das Capenische Tor schaut.
Von den
fünf Wörtern nimmt PORTA die Mitte der Zeile ein.
|
|
Die 30 Buchstaben
hat Ovid so gewählt, daß nicht mehr als 4 T, 4 E und 1 N das TENET-Kreuz bilden
und ein einziges R die Darstellung eines einzigen Tores, der PORTA CAPENA
ermöglicht. Die Buchstaben OPA hingegen sind mehr als einmal vertreten. 5 Buchstaben
sind zusätzlich zu plazieren. Die ZS der
vorstehenden Grafik geben die ZS der horizontalen und vertikalen
Zeilen des SATOR-Quadrats
wieder, nicht allerdings der diagonalen. Eine optimalere Anordnung der 20 Buchstaben
dürfte möglich sein.
Die ZS+FS
246 = 6*41 von SATOR+ROTAS entspricht der FS der Rahmenelemente
(Außenelemente) des DR-Kreuzes nach den beiden Numerierungsweisen (165+246
= 411).
Die ZS+FS der ersten beiden und letzten beiden
Wörter ist 2*(121+94) = 430. Durch 43 teilbar sind die konzentrischen Innenelemente der 24-er Numerierung, z.B. 19+24.
7.
Die ZS von SATOR
selbst ist unter anderem auch zusammengesetzt aus einer ZS+FS, nämlich der Zahlen 1-8, aus 36+33 = 69. Nehmen wir OT für 33, ergeben sich angrenzenden ZS+FS:
|
|
ZS |
FS |
sm |
|
ARS |
36 |
26 |
62 |
|
OT |
33 |
28 |
61 |
|
sm |
69 |
54 |
123 |
Es zeigt sich, daß es auch im DR-Kreuz selbst einen Austausch von innen und außen gibt, der
sich in der ZS+FS des Wortes SATOR widerspiegelt: Die FS 246 der Außenelemente des DR-Kreuzes ist doppelt so groß
wie die ZS der 6
Innenelemente der 23-er Numerierung. Die ZS 1-23 ist 12*23
und entspricht viermal den Wörtern SATOR-ROTAS
im umlaufenden Quadratrahmen.
Die Wörter SATOR-ROTAS sind also als Außenelemente dem
Rahmen des DR-Kreuzes zuzuordnen, die Zeilen 2-4
den Innenelementen. Das ZS-Verhältnis der beiden Teile beträgt 138:165 = 3*(46:55) = 3*101. Beide Klammerwerte beziehen sich
auf die FS und ZS
der Zahlen 1-10. Wenn jede der drei DR sich mit jeder verbindet, ergeben sich drei Oktaeder aus 3 DR-Kreuzen.
Die zu den Innenelementen gehörige ZS 55 trägt
dem Umstand Rechnung, daß die beiden Querlinien einer DR die Zahl von 10 Maßeinheiten vervollständigen.
Die ZS 303
des SQ hat also eine doppelte
Zusammensetzung: aus den FS
102 und 201 der Zahlen 1-16 und 1-23
und der dreifachen ZS+FS der Zahlen 1-10. Eingegliedert ist dabei die
zweifache ZS+FS der Zahlen 1-8 der Wörter SATOR-ROTAS.
c) Trinitarische Begründungen
1. Die trinitarische Bedeutung der Zahlen 16
und 17 gründen auf ihren Zusammensetzungen 9+7
und 9+8, insofern diese gemäß den Grundzahlen 1-9
symmetrische Entsprechungen zu 1+3 und 1+2 sind. Die dreistellige Zusammensetzung der
komplementären Zahlenpaare ergibt 33-7/7-33. Darin kann man 3+3 Ecken des
Tetraktyssterns und die 7 Punkte des Hexagons sehen.
2. 16 und 17 bilden die Mitte der Zahlen 12 bis 21,
deren Verhältnis 3*(4:7) beträgt. Zweistellige Umkehrzahlen stellen modellhaft
zwei Hälften dar, wobei die zweite Hälfte zum Ausgangspunkt zurückführt:
|
|
Die Zahl 121 mit ihren
Faktoren 11*11 hat eine bedeutsame Parallele in der Doppelraute, die
aus zweimal 11 Elementen besteht und auch in den 12
Punkten + 10 Maßeinheiten der zwei
Achsenfiguren.
3. In konzentrischer Paarung ergeben die
Zahlen 16+24 und 17+23 jeweils 40 = 5*8.
Die Zahlen 5 und 8 stellen zweimal zu zählende Radialelemente des
Tetraktyssterns dar, die 1+2 und 1+3 Flächeneinheiten vertreten:
|
|
IV. Numerierungen der
DR-Punkte
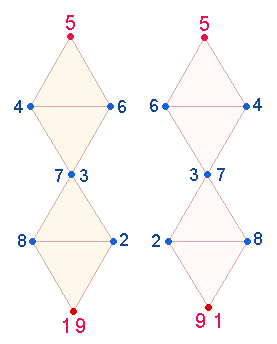
1. Für die Grundlegung des Dezimalsystems
ist die ebenfalls schleifenförmige Numerierung der DR-Punkte
von Bedeutung:
|
|
In horizontaler Nebeneinanderstellung
ergänzen sich die Einzelziffern jeweils zu 10 mit 5
als Symmetriemittelpunkt. Behandelt man sie als zweistellige Zahlen, kommt bei
der Zusammenlegung der äußeren Punkte zum Zweck der Oktaederbildung neben der
Zahl 5 die Zahl 19 zu stehen, woraus sich gematrisch die Buchstaben ET – und
ergeben. Die Wortbedeutung stimmt also mit dem Vorgang des Verbindens zweier gegenüber
liegenden Punkte überein. Die Umkehrung TE – dich bedeutet eine
kommunikative Verbindung auf personaler Ebene.
Im TENET-Kreuz kommt das TE
viermal vor, hat also die ZS
96, die dem Umkehrwert 91+5
entspricht.
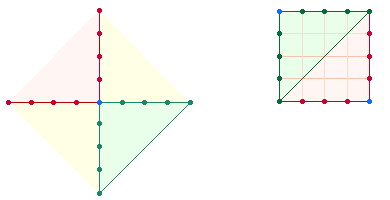
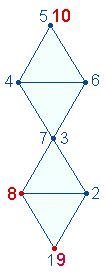
2. Die dargestellte DR-Numerierung
zeigt enge Übereinstimmung mit dem ausgeschnittenen 1*1
Quadrat ohne Zehnerstellen:
|
|
|
Die Ziffern der DR-Numerierung
sind kreisförmig zu lesen, um sie in Übereinstimmung mit den Ziffern des
Quadrates zu bringen, unten gegen den Uhrzeigersinn, oben im
Uhrzeigersinn. Die Zahlen 6
und 4 bilden die Eckbuchstaben
der inneren 5x5-Tabelle. Im SQ ist die ZS
der inneren Eckbuchstaben 64, die sich durch 4 E haben in
Übereinstimmung mit 2*(6+4) auf 84 vergrößert.
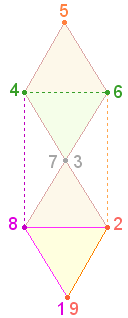
3. Wenn man, wie bei der 24-er Zählung, die
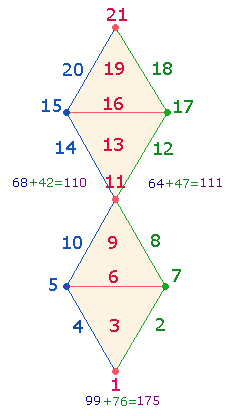
Numerierung zum gegenüberliegenden Punkt fortsetzt, wird man, der Kreisnumerierung entsprechend, einmal zur Null fortschreiten und einmal zur Zahl 10:
|
|
Auch die zwei neuen Doppelpositionen
können zusammengesetzt als 50 und 510 gelesen und mit der Zahl 19
verbunden werden. Das erste Additionsergebnis 69 ist identisch
mit der ZS von SATOR, das zweite 529 ist die Quadratzahl
von 23.
Die Zahl 50 gibt auch das
Muster für das Achsenkreuz des ausgeschnittenen 1x1-Quadrates wieder.
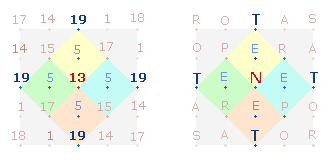
1.
Die
zwei Quadratachsen haben jeweils die ZS 61. Als einfachste
Erklärung bietet sich die doppelte Addition von 6+1 Punkten der
beiden konzentrischen Tetraktyskreise an, deren Flächenverhältnis 1:3 beträgt. Die Einzelziffern des Additionsergebnisses 122
weisen auf die 5 Radialelemente des Tetraktyssterns hin.
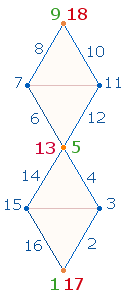
Die Zahlen 5
und 13 bilden die Mitte der Numerierung des DR-Rahmens
1-17 und damit übereinstimmend des 1x1-Quadrats sowie des SATOR-Quadrats. In
letzterem Fall ist 13 die symmetrische Mitte von 25
Buchstaben.
2.
Die
4 T, die das Mittelpunkt N = 13
umgeben, haben die ZS 76. Was die Ziffern 7 und 6 mit
4*19 zu tun haben, ist etwa folgendermaßen zu erklären:
Die drei Hexagonachsen bestehen aus 7
Punkten und 6 Linien. Sie entfalten sich zu zwei Tetraktys mit je
drei Seiten aus 9 Punkten und 9 Linien. Hinzukommt der
Mittelpunkt, sodaß die 13 Elemente der Hexagonachsen von 10
Punkten und 9 Linien der Tetraktys eingerahmt werden:
|
|
Die Zahlen 7 und 6
sind die FW von 10 und 9. Außer den 9 Linien können sich die 10
Punkte auch mit 9 Dreiecken verbinden. Auf diese Weise läßt sich die
Zahl 19 in jeder Tetraktys zweimal zählen.
Die Zahlenentsprechungen 15
und 17 für P und R beziehen sich auf die Rahmenelemente der DR,
einmal in normaler und einmal in schleifenförmiger Zählung. Die Zahl 5 befindet
sich im Mittelpunkt bei der Numerierung der 10 Tetraktyspunkte und der
schleifenförmigen Numerierung von 1-17. Auf diese Weise
verbindet ein kleines Rautenquadrat Tetraktys und Doppelraute.
Geht man von 74 Elementen für zwei
Tetraktys aus, könnten die beiden konzentrischen Kreisbögen als 2
weitere Elemente hinzugefügt werden.
3. Die 4 T
und das N haben die ZS 89. Es ist hier real an
zwei numerierte Achsenarme von je 9 Elementen zu denken.
Belegt man für 13 die Zahl 6-1-6, bleibt auf jedem
Achsenarm die Numerierungssumme 38:
|
|
4.
Die
ZS 109 des TENET-Kreuzes weist auf den Doppelaspekt von 10
Radial- und 9 Durchmesserelementen des Tetraktyssterns hin ebenso
wie auf die 19 Elemente des Tetraktysrahmens einschließlich
Mittelpunkt. Das Ergebnis der Doppelzählung, 109+122 = 231 =
21*11, zeigt die Bedeutung der Zahl 21
für 10 Maßeinheiten, die durch 11
Punkte begrenzt werden. Dabei kann der FW 10 der Zahl 21
für die Maßeinheiten stehen.
In ihren Einzelziffern gibt die Summe die Numerierung
der Kreisachse wieder, wenn man von außen zum Mittelpunkt hin liest:
|
|
5. Durch die Doppelzählung des TENET-Kreuzes
sind in den 21 Buchstaben der drei Mittelzeilen (horizontal und
vertikal) die ZS 231 und die FS 165 der Zahlen 1-21
vereint. Gibt man dem Achsenkreuz aus 9 Buchstaben die volle
Priorität, erbringen deren ZS+FS
und die der übrigen 12 Buchstaben folgendes Ergebnis:
|
|
ZS |
FS |
sm |
FW |
sm |
|
9 Bu. |
109 |
109 |
218 |
111 |
|
|
12 Bu. |
124 |
90 |
214 |
109 |
|
|
sm |
233 |
199 |
432 |
220 |
|
|
FW |
|
|
17 |
20 |
37 |
Das ZS+FS-Verhältnis der beiden Buchstabengruppen ist 2*(109:107). Das ZS+FS
der 21:4 Buchstaben ist 432:120 = 24*(18:5).
Die Zahlen 18 und 5 bilden eine Numerierungseinheit in der Tetraktys von 3 Eckpunkten und
dem Mittelpunkt.
1.
Das
Produkt 11*21 = 231 kann durch Numerierung der 21
DR-Elemente erreicht werden. Die Zahlen sind im Zickzackmodus von unten nach
oben eingetragen:
|
|
Die 21 Zahlen sind aufgeteilt
in 4*3 Außenglieder und 9 Innenelemente. Das
Muster von links-Mitte-rechts ist 6-9-6. Der FS
76 entsprechen die 4 T des TENET-Kreuzes. Durch Hinzufügung der Mittelpunktszahl 13
für das N erhöht sich die ZS auf 89,
die mit der FS der 12 Zahlen des DR-Rahmens (42+47) übereinstimmt. Auf diese Weise wird durch Doppelzählung 76+(76+13) die FS 165 erreicht.
2.
Von
den 6 Summen können noch die FW ermittelt
werden:
|
|
ZS |
FW1 |
sm |
FS |
FW2 |
sm |
GS |
|
links |
68 |
21 |
89 |
42 |
12 |
54 |
143 |
|
rechts |
64 |
12 |
76 |
47 |
47 |
94 |
170 |
|
Mitte |
99 |
17 |
116 |
76 |
23 |
99 |
215 |
|
sm |
231 |
50 |
281 |
165 |
82 |
247 |
528 |
Die FW1/2 betragen 50+82
= 132 und bilden so mit der ZS+FS 231+165
= 396 das Verhältnis 132*(1:3) und das Differenzverhältnis 1:2.
Die FW1 der ZS
entsprechen den Umkehrzahlen 12 und 21 und deren FW 7+10 = 17.
Die erwähnten Summen des TENET-Kreuzes
76 und 89 kommen auch als
Addition von ZS und deren FW vor.
Die Summe 281 ist als 28+1
zu lesen und gibt die Zahl der Rahmenelemente des DR-Kreuzes
wieder.
Die Summe 247 besteht aus den
Faktoren 13*19, denen die Buchstaben NT
des TENET-Kreuzes entsprechen.
Die Summe 143
ist die ZS der Wörter PATER NOSTER des SQ
und bildet mit den beiden anderen Summen 170+215 das Verhältnis 11*(13:35).
3. Die ZS 52+61+52 der drei Mittelzeilen erscheinen als FS der bei einer weiteren Numerierungsweise nach dem Muster 6-9-6: Die Numerierung
beginnt mit 7 Punkten und wird durch 4 Dreiecke und 10
Linien fortgesetzt.
VII. Strukturelle und gematrische Folgerungen
1.
Im
SQ sind zwei strukturelle Prinzipien festzustellen: das Prinzip der Ganzheit und zweier Hälften und das Prinzip des Außen und Innen.
Eine Ganzheit bilden die 5 Buchstabenzeilen, zwei Hälften jeweils 3
Buchstabenreihen. Als Prinzip des Innen und Außen wurden die 3
mittleren und die 2 äußeren Zeilen erkannt. Sie ergänzen die Aufteilung
des Innen und Außen, die aus der Mittelzeile und den symmetrischen
Außengliedern von je zwei Zeilen besteht.
2.
Als
Modell beider Prinzipien ist die Kreisachse und das hexagonale Dreieck
anzusehen. Die 5 DM-Elemente teilen sich in 2*3
Radialelemente, das hexagonale Dreieck wird bei der Bildung des Tetraktyssterns
spiegelsymmetrisch nach außen gefaltet und wird zweimal zur Raute.
Zu den 7 Elementen des Dreiecks treten noch 4
weitere hinzu. Wie bereits erwähnt, läßt sich der Doppelaspekt von 5 DM- und 6 Radialelementen in 4
Radialelemente + 7 Punkte aufteilen.
3.
Die
beiden strukturellen Prinzipien haben gematrische Entsprechungen: Die ZS der äußeren beiden Zeilen (69+52 = 11*11) sowie die drei mittleren Zeilen (52+61+52 = 15*11) sind durch 11 teilbar.
Analoge Teilbarkeit durch 47 gilt für die FS: 54+40
= 2*47; 40+61+40 = 3*47.
Die zweite bzw. vierte Zeile erweist sich so als Bindeglied, wie ein Radialmaß
als Verbindung zweier Punkte angesehen werden kann. Die Verklammerung der 5
Zeilen verwirklicht sich gematrisch also in der doppelten Zählung der 2. und 4.
Zeile nach dem Muster 2-3-2. Die ZS+FS
dieser Gruppierung beträgt demnach (11+15+11)*11 und (2+3+2)*47 = 407+329
= 736 = 23*32.
Die Ganzheit und zwei Hälften (3+3) haben folgende
Werte:
|
|
ZS |
FS |
sm |
|
5 Z. |
303 |
249 |
552 |
|
2*3 Z. |
364 |
310 |
674 |
|
sm |
667 |
559 |
1226 |
Die Gesamtheit der ZS+FS beträgt nun:
|
Zeilen |
11 |
7 |
sm |
|
ZS |
667 |
407 |
1074 |
|
FS |
559 |
329 |
888 |
|
sm |
667 |
736 |
1926 |
|
1962 = 18*109 |
|||
Da es sich um 11+7
= 18 Buchstabenzeilen handelt, ist die durchschnittliche ZS+FS je 5
Buchstaben 109. (s.a. Binnenstrukturen des SQ)
Die Zahl 109 ist bereits
bekannt als ZS des TENET-Kreuzes. Die 18 Zeilen lassen sich
einteilen in drei vollständige Quadrate und den zusätzlichen Zeilen 2,3,4,
also in 15+3 Zeilen. Die drei
TENET-Kreuze aus 27 Buchstaben haben somit
die ZS+FS
6*109
und bilden zu den übrigen 63 Buchstaben das Verhältnis 1:3.
Die ZS+FS der drei Mittelzeilen beträgt 165+141 = 306
= 17*18, die der drei vollständigen Quadrate 3*23*24 = 92*18. Das ZS+FS-Verhältnis
der 15:3 Zeilen ist demnach 18*(92:17).
4.
Bei
der 24-er Numerierung der DR werden die 15
Elemente des DR-Rahmens um 2+1
erweitet. Die Zahlen 17 und 18 stehen sich dabei wie im Wort ROTAS
gegenüber.
Die schleifenförmige Numerierung der DR-Punkte
und der DR-Punkte + Rahmenlinien entspricht den
Elementen der ersten beiden Achsenkreuze:
|
|
|
|
|
Ein zweiter unsichtbarer Mittelpunkt der Achsenkreuze
ergibt 10 bzw. 18 Elemente wie in den DR, die durch
Vereinigung der äußeren Punkte eine weitere Numerierungsposition liefern.
Das SQ verbindet die Zahlen 9 und 1
der 5*5-Tabelle mit den ZW 18 und 17
der Buchstaben S und R:
|
|
|
|
|
|
5.
Weitere strukturelle Gesichtspunkte (zeitlich
weiter zurückliegend)
Erstellt: September 2001
Neu bearbeitet: Dezember 2010
Letzte Änderung: April 2020