B. 6 Achsen des Dezimalsystems
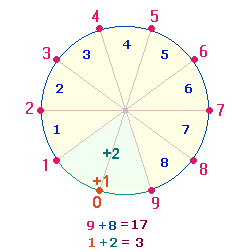
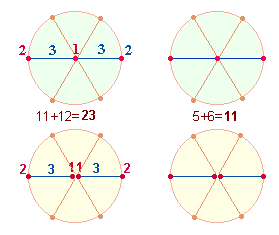
I. 5+6
Achsen
II. IVPPITER
IVNO
c)-i) 4Werte;
SATOR-Quadrat
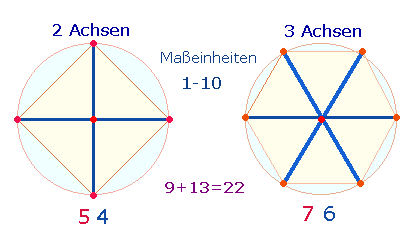
I. 5+6 Achsen
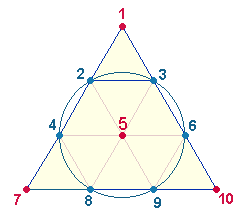
1. Im ersten Teil wurden 5+1 Achseneinheiten (AE) behandelt. Grundlage sind die Zahlen 1-30 und 31-36. Eine Maßeinheit wird jeweils von zwei Punkten begrenzt. Daher fallen die ersten beiden Maßeinheiten auf die Zahlen 2 und 5, während 1 3 und 4 6 Begrenzungspunkte sind. Die für das Dezimalsystem wichtigen 10 Maßeinheiten reichen nur bis zur Zahl 30, sie sind in zwei Achsenfiguren enthalten:
|
|
Die Logik erfordert auch eine geometrische Figur aus einer Achse, dies ist die Kreisachse. Da nun die Zahlensummen (ZS) + Faktorensummen (FS) der Zahlen 1-30 33*23 und der Zahlen 1-36 33*32 betragen und die Einzelziffern jeweils 3+3 Radialelemente und 5 Durchmesserelemente bedeuten, liegt es nahe, eine Addition der Zahlen 1-30 und 1-36 vorzunehmen.
2. Da eine Achse jeweils zwei Maßeinheiten enthält, lassen sich jeweils zwei Maßeinheiten zu einer Achseneinheit (AE) zusammenfassen. Entsprechend den 5 Durchmesser- und 6 Radialelementen einer Achse können wir die 5 und 6 Achsen auf eine einzelne Achse legen, indem wir sie den 5 Durchmesser- und 6 Radialelementen zuordnen. Jede Kreisachse bedeutet entweder je einen Kreis und jeweils zwei Kreishälften oder die 5 Durchmesser- und 6 Radialelemente werden zu einem Achsenkreuz verbunden, das zu einem Quadrat weiterentwickelt werden kann:
3. Folgende Zahlensummen (ZS) und Faktorensummen (FS) ergeben sich:
|
AE |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
1-6 |
7-12 |
13-18 |
19-24 |
25-30 |
31-36 |
sm |
|
ZS |
21 |
57 |
93 |
129 |
165 |
201 |
666 |
|
FS |
20 |
44 |
63 |
83 |
84 |
96 |
390 |
|
|
41 |
101 |
156 |
212 |
249 |
297 |
1056 |
Die ZS+FS der ersten 5 Achseneinheiten können zweimal von einer Seite zur anderen angeordnet werden, die 6. Achseneinheit folgt am Ende als zweiter Mittelpunkt. Auch andere Anordnungen sind möglich, ich beschränke mich auf diese eine:
|
41 |
101 |
156 |
212 |
249 |
|
|
41 |
101 |
156 |
297 |
212 |
249 |
Durch diese Anordnung wird die konzentrische Mitte zum Mittelpunkt, während die Konstruktion des Kreises vom Mittelpunkt selbst ausgeht und sich nach beiden Seiten ausdehnt. Durch die lineare Anordnung entsteht eine Unterscheidung zwischen Punkten und Maßeinheiten, das Verhältnis der Maßeinheiten zu den Punkten ist 4:7.
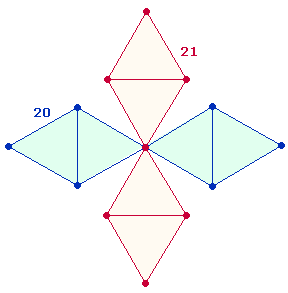
Die Summe 101 der zweiten AE stellt verkürzt 10 Maßeinheiten und 11 Punkte dar, zusammen 21 Elemente der Doppelraute (DR). Die Summe 212 der vierten AE zeigt das Muster der Kreisachse aus Mittelpunkt und zweimal zwei spiegelbildlichen Elementen von Punkt und Maßeinheit. Die Einzelziffern der beiden addierten Summen 313 geben die Punktestruktur der DR wieder. In der Verdoppelung bilden sie ein Doppelrautenkreuz, aus dem ein Oktaeder zusammengefügt werden kann.
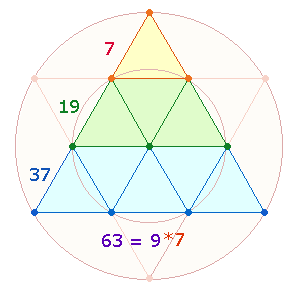
4. Die ZS+FS der 3 Mittelpunkte und 4 Kreislinienpunkte sind durch 29 teilbar: 609:580 = 29*(21:20) = 29*41 = 1189 = FW 70. Aus 21+20 Elementen besteht ein DR-Kreuz, aus 29 Elementen dessen Rahmenelemente:
|
|
|
Der FW 70 = 7*10 weist auf 7 Punkte des Hexagon und 10 Punkte der Tetraktys hin. Sie geben das Kreisflächenverhältnis 1:3 wieder.
5. Die Bedeutung der Punkte- und Linienwerte erschließt sich durch die ZW/FW-Verrechnung:
|
|
P |
L |
sm |
FW |
sm |
FW |
sm |
|
ZS+FS |
1189 |
626 |
1815 |
30 |
|
|
|
|
FW |
70 |
315 |
385 |
23 |
|
|
|
|
sm |
|
|
2200 |
53 |
2253 |
754 |
3*751 |
|
FW |
|
|
27 |
53 |
80 |
13 |
|
|
sm |
|
|
|
|
2333 |
767 |
59*13 |
|
FW |
|
|
|
|
2333 |
72 |
2405 |
|
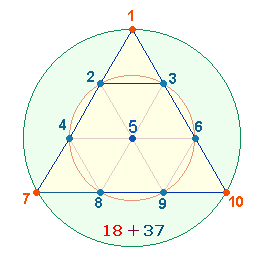
2405 = 5*13*37 >FW 18+37 = 55 |
|||||||
Die Einzelziffern der FW 30 und 23 bezeichnen 3 Radialelemente des Hexagon und des äußeren Tetraktyskreises in der Aufteilung 2+3. Die Ziffern geben das Kreisflächenverhältnis 1:3 wieder. In der Primzahl 2333 erkennt man 2+3 DM- und 3+3 Radialelemente des Hexagon.
Die Einzel-FS 18 und 37 entsprechen in einer numerierten Tetraktys den 3 Eckpunkten und den 7 hexagonalen Punkten:
|
|
18*37 ist die Summe der Zahlen von 1-36.
6. Von den zahlreichen Verrechnungsmöglichkeiten wähle ich zwei aus. Zunächst sollen von den ZS+FS der 5+1 Achseneinheiten die FW ermittelt werden:
|
|
1 |
2 |
3 |
4 |
5 |
sm |
6 |
GS |
|
ZS+FS |
41 |
101 |
156 |
212 |
249 |
759 |
297 |
1056 |
|
FW |
41 |
101 |
20 |
57 |
86 |
305 |
20 |
325 |
Nun sind die 4Werte der ermittelten Summen zu errechnen:
|
ZS+FS |
FW-S |
sm |
FW1 |
FW2 |
sm |
GS |
|
759 |
305 |
1064 |
37 |
66 |
103 |
1167 |
|
1056 |
325 |
1381 |
24 |
23 |
47 |
1428 |
|
1815 |
630 |
2445 |
61 |
89 |
150 |
2595 |
|
2595
= 15*173 = FW 181 |
||||||
Die FW 24 und 23 der 6 AE geben in den Einzelziffern die 6 Radial- und 5 DM-Elemente wieder. Die Zahl 173 stellt, aufgeteilt in 9+8 und 1+2, Komplementärzahlen und 10 Punkte und 10 Maßeinheiten im Kreis dar:
|
|
Im Kreis fallen im Punkt 0 zwei Begrenzungspunkte zusammen. Daher begrenzen 1+9 Punkte 1+8+1 Maßeinheiten. Dies wird durch die Zahl 2595 ideal dargestellt.
7. Von den 5 AE können nach Punkten und Maßeinheiten die 4Werte bestimmt werden. Diese sind:
|
ZS P |
14 |
38 |
62 |
86 |
110 |
310 |
FS P |
13 |
27 |
37 |
51 |
40 |
168 |
478 |
|
FWS P |
9 |
21 |
33 |
45 |
18 |
126 |
FW P |
13 |
9 |
37 |
20 |
11 |
90 |
216 |
|
ZS ME |
7 |
19 |
31 |
43 |
55 |
155 |
FS ME |
7 |
17 |
26 |
32 |
44 |
126 |
281 |
|
FWS ME |
7 |
19 |
31 |
43 |
16 |
116 |
FW ME |
7 |
17 |
15 |
10 |
15 |
64 |
180 |
|
|
|
|
|
|
|
707 |
|
|
|
|
|
|
448 |
1155 |
|
180:216 = 36*(5:6) = 36*11 |
||||||||||||||
Von Interesse sind die
Zahlenverhältnisse FW-Summen der
nach Punkten und Maßeinheiten aufgeteilten ZS und FS. Es handelt sich um die jeweiligen 4Werte:
|
ZS |
FS |
sm |
FWS1 |
FWS2 |
sm |
GS |
|
310 |
168 |
478 |
126 |
90 |
216 |
694 |
|
155 |
126 |
281 |
116 |
64 |
180 |
461 |
|
465 |
294 |
759 |
242 |
154 |
396 |
1155 |
|
154:242= 22*(7:11); |
||||||
|
396:759
= 33*(12:23) = 33*35 |
||||||
Erstaunlich ist, daß die FW-Summe 396 wie die ZS+FS 759 durch 33 teilbar ist. Die Produktzahlen 33*35 stellen zwei Achsenkreuze AK5 mit einem und zwei Mittelpunkten dar. Die Einzelziffern der Verhältniszahlen 12:23 sind chiastisch auf die Entsprechung von 2 und 3 Radialelementen zu 2 und 1 Kreisflächeneinheit zu beziehen. Die Zahl 396 ist die ZS+FS der Zahlen 1-21: 231+165 = 396.
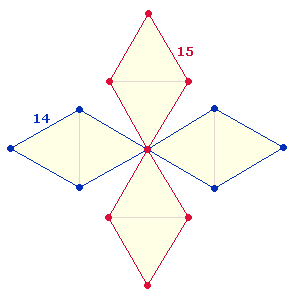
Die 4Werte der sechsten Achseneinheit sind:
|
|
ZS |
FS |
sm |
FWS1 |
FWS2 |
sm |
GS |
|
P |
134 |
74 |
208 |
69 |
39 |
108 |
316 |
|
ME |
67 |
22 |
89 |
67 |
13 |
80 |
169 |
|
|
201 |
96 |
297 |
136 |
52 |
188 |
385 |
|
13:39
= 13*(1:3); 385 = 5*97 = FW 102 |
|||||||
188 ist die ZS+FS 112+76 des Namens CHRISTUS. Die Einzelziffern stellen die Elemente des Achsenkreuzes AK3 dar.
Die gefundenen Werte sind den vorherigen hinzuzufügen:
|
|
ZS |
FS |
sm |
FWS1 |
FWS2 |
sm |
GS |
|
P |
444 |
242 |
686 |
195 |
129 |
324 |
1010 |
|
ME |
222 |
148 |
370 |
183 |
77 |
260 |
630 |
|
|
666 |
390 |
297 |
378 |
206 |
584 |
1640 |
Bemerkenswert sind die Summen 370 und 260, da sich die drei Dreiecksstufen der Tetraktys aus 7+19+37 = 26+37 Elementen zusammensetzen:
|
|
Die zwei 4W-Summen
betragen 1155+1640 =
2795 = 5*13*43 = FW
61. Der Faktor 13
der Gesamsumme ist bereits in der vereinten ZS enthalten.
Hierbei wird der Faktor 31 der Summe der Zahlen
von 1-30 = 15*31 = 465 durch Verdoppelung und
Hinzufügung von 201 der Zahlen 31-36 in den Umkehrfaktor verwandelt: 465+(465+201) = 1131 = 3*13*29 = 87*13, hinzukommt
die FS 390 = 30*13 der Zahlen 1-36, zusammen 117*13 = 9*13²
= 39². Es bleiben übrig die FS 294 der Zahlen 1-30
und die FW-Summen 396+584 =
980. Die beiden Werte bilden das Verhältnis 98*(3:10)
= 98*13. Dieses Verhältnis ist
auf 10 Tetraktyspunkte und 3 weitere Eckpunkte des Hexagramms zu beziehen.
8. Die FW der beiden Gesamtsummen 1155 und 1640 sind 26+52 = 78 = 6*13 und erhöhen somit die 4W-Summe 2795 zu 13*(215+6) = 13*221 = 13²*17 = FW 43. Aus 26 Elementen und 4 Doppeldreiecken zu je 13 Elementen besteht der Oktaeder.
Eingangs wurden die 5+6 Achsen auf eine einzelne Kreisachse gelegt, indem sie den 5 Durchmesser- und 6 Radialelementen zugeordnet wurden. Jede Kreisachse bedeutet demnach je einen Kreis oder zwei Kreishälften. Die Verdoppelung ist auch in den FW 26 und 52 zu erkennen und auf den Oktaeder zu beziehen: Er besteht aus 26 Elementen als ganzer und aus zwei Hälften von je 2 Doppeldreiecken zu je 13 Elementen.
Eine ZW/FW-Verrechnung der beiden Summen 1155 und 1640 ergibt:
|
|
P |
L |
sm |
FW |
sm |
FW |
|
4WS |
1155 |
1640 |
2795 |
61
|
|
|
|
FW |
26 |
52 |
78 |
18 |
|
|
|
sm |
|
|
2873 |
79 |
|
|
|
FW |
|
|
43 |
79 |
122 |
63 |
|
2873 = 13²*17; 122 =
2*61 |
||||||
Die Zahl 61 kommt
zweimal vor. 2*61 läßt sich auf je 7 Punkte von 2 Doppelrauten beziehen, aus denen
sich ein Oktaeder zusammenfügen läßt. Das TENET-Kreuz
des SATOR-Quadrats
ist hierfür ein gewichtiges gematrisches Zeugnis. Die Zahl 2873 besteht aus zwei Paaren von komplementären
Zahlen der Grundzahlen von 1-9. Man kann an 2+8 Linien der Doppelraute und 7+3 Punkte der Tetraktys denken, weiterhin an
numerierte Rahmenelemente der Summen 2*8 + 3*7
eines DR-Kreuzes.
Eine weitere Deutung ergibt sich aus den Numerierungssummen 28 und 45 der Zahlen 1-7 und 1-9. 73 ist somit zusammengesetzt aus 28+45. Die Zahlenfolge 779 stellt die Elemente zweier Kreishälften und des ganzen Kreises mit Kreisachse dar:
|
|
Die Zahl 9 ist in diesem Zusammenhang der FW von 2*7 = 14.
Der Aspekt zweier Hälften ist auch aus den Faktoren von 2873 = 13*13*17 zu ersehen: Denn eine Oktaederhälfte besteht aus 8 Elementen der Mittelbasis und 9 Elementen des pyramidalen Aufbaus. Die andere Hälfte ist aus zwei Doppeldreiecken zu je 13 Elementen zusammensetzbar.
II. IVPPITER IVNO
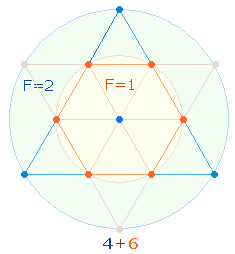
1. Die beiden geometrischen Figuren des hexagonalen und des rechtwinkligen Achsenkreuzes sind konstitutiv für das Dezimalsystem, da sie 6+4 = 10 Maßeinheiten enthalten. Ebenso bedeutsam sind 6+4 Punkte der Tetraktys:
|
|
|
6:4 Punkte geben das trinitarische KreisFlächenverhältnis 3:1 wieder. In der numerierten Tetraktys ist das Summenverhältnis 32:23, oder bei 4:6 Punkten, 23:32.
2. Die römischen Zahlzeichen für die Zahlen 4 und 6 sind die Buchstaben IV und VI. Es liegt nahe, hier einen Zusammenhang zu sehen zwischen den Zahlen 1-30 (2+3 Achsen) und 1-36 (5+1 Achsen), da die ZS+FS der beiden Zahlenfolgen 33*23 und 33*32 beträgt. Zwar bedeutet IV 5-1 = 4, aber man kann beide Zahlzeichen auch addieren. Damit ist die Frage berührt, an welcher Stelle die 1. Achse stehen soll: 6+4 = 10 Maßeinheiten schließt die erste Achse, die am Anfang stehen sollte, zunächst aus, sie wird also an 3+2 Achsen angehängt. Diesem Doppelaspekt wird durch die Zahlzeichen IV und VI Rechnung getragen. Dazwischen steht das einfache Zahlzeichen V. Man kann daher lesen (1+5)+5 und 5+(5+1), so daß die Zahlen 1-30 und 1-36 zweimal addiert werden. Die entsprechenden lateinischen Zahlzeichen IVV VVI haben jeweils den Buchstaben- und Zahlzeichenwert 49+11 = 60 und die FW 24+11 = 35; das FS:ZS-Verhältnis ist 5*(7:12).
3. Die Lesart IVV VVI gibt Veranlassung, die jeweils erste und zweite Radialeinheit (RE) einer Achse getrennt zu berechnen. Die Maßeinheiten (ME) schreiten im Sechserabstand voran: 2-8-14-20-26|32; 5-11-17-23-29|35.
|
1.RE |
ME |
AE |
AE |
Pu. |
AE |
AE |
|
||
|
|
1-30 |
31-36 |
6 |
5+5+1 |
1-30 |
31-36 |
6 |
5+5+1 |
5+6 |
|
ZS |
70 |
32 |
102 |
172 |
140 |
64 |
204 |
344 |
516 |
|
FS |
41 |
10 |
51 |
92 |
86 |
45 |
131 |
217 |
309 |
|
|
111 |
42 |
153 |
264 |
226 |
111 |
335 |
561 |
825 |
|
264:561 = 33*(8:17) = 33*25 |
|||||||||
|
2.RE |
ME |
AE |
AE |
Pu. |
AE |
AE |
|
||
|
|
1-30 |
31-36 |
6 |
5+5+1 |
1-30 |
31-36 |
6 |
5+5+1 |
5+6 |
|
ZS |
85 |
35 |
120 |
205 |
170 |
70 |
240 |
410 |
615 |
|
FS |
85 |
12 |
97 |
182 |
82 |
29 |
111 |
193 |
375 |
|
|
170 |
47 |
217 |
387 |
252 |
99 |
351 |
603 |
990 |
|
387:603 =
9*(43:67) |
|||||||||
|
825:990 = 11*15*(5:6)
= 165*11 |
|||||||||
Das Verhältnis 5:6 der 11 ersten und 11 zweiten Radialeinheiten entspricht der Addition von 5+6 Achsen der Zahlen 30+36 = 66. Geometrischer Bezugspunkt sind die drei Doppelrauten des Tetraktyssterns. Eine einzelne Raute besteht aus 11 Elementen: 5 Maßeinheiten und 4 Punkten + 2 Dreiecksflächen. Indem jede Maßeinheit zwei eigene Zahlen als Begrenzungspunkte erhält und 5+6 Achsen addiert werden, erhöht sich die Zahl der Elemente von 22 der beiden grundlegenden Achsenkreuze des Dezimalsystems auf 66, dem Dreifachen.
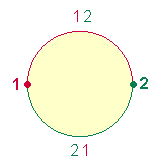
4. Hintergrund für die Zahl 165 sind die Zahlen 12 bis 21, deren Summe die 10 Zahlen sind: 5*(12+21) = 5*33 = 165. Die beiden Zahlen 12 und 21 lassen sich aus der Numerierung zweier Kreisbogenhälften zusammensetzen:
|
|
Die Bestimmung zweier gegenüberliegenden Punkte auf der Kreislinien bildet den Anfang einer rationalen Differenzierung dessen, was außerhalb aller rationalen Faßbarkeit liegt, wie die Endlosigkeit der Kreiszahl p zeigt. Indem die zweite Kreislinienhälfte zum Anfang zurückkehrt, beinhalten die Zahlen 12 bis 21 symbolisch die Unendlichkeit Gottes. Die 10 Zahlen sind auch ein Hinweis auf die universale Gültigkeit des Dezimalsystems.
In den Faktoren 3*5*11 dürften die Eigenschaften der drei Hexagonachsen zusammengefaßt sein: 3 Achsen aus je 5 Durchmesserelementen und entweder der Doppelaspekt von 5 DM-Elementen + 6 Radialelementen oder der Numerierungssumme 11:
|
|
Die Faktoren 11 und 15 könnten auch in der Zahl 56 enthalten sein 5+6 = 11, 7*8 = 56. Aus 7 Punkten und 8 Linien besteht der DR-Rahmen. Der Name IUNO läßt sich zu UNIO – Vereinigung umstellen. Die trinitarischen Bezeichnungen PATER FILIUS SANCTUS SPIRITUS bestehen aus 5+6 und 7+8 Buchstaben.
Nicht nur die Summe der Zahlen von 12-21 beträgt 165, sondern auch die FS der Zahlen 1-21.
5. Von I und V lassen sich die ZS und FS sowohl hinsichtlich ihrer Buchstabenposition (ZW) als auch ihrem Zahlzeichenwert (ZZ) ermitteln:
|
|
ZW |
ZZ |
sm |
FW |
FW |
sm |
GS |
|
I |
9 |
1 |
10 |
6 |
1 |
7 |
17 |
|
V |
20 |
5 |
25 |
9 |
5 |
14 |
39 |
|
sm |
29 |
6 |
35 |
15 |
6 |
21 |
56 |
|
21:35 = 7*(3:5) |
|||||||
Die Gesamtsumme 56 weist in ihren Einzelziffern auf den Doppelaspekt von 5 DM- und 6 Radialelementen hin, durch die Faktoren 7*8 aber auch auf die 7 Punkte und 8 Linien des DR-Rahmens. Die Verhältniszahlen 3:5 bezeichnen die Radialelemente des Hexagons und der DR, die als externes Verhältnis das Kreisflächenverhältnis 1:3 und als internes Differenzverhältnis 3:2 Flächenverhältnis 1:2 wiedergeben.
1. Die Buchstabenverbindung IV erscheint also besonders bedeutsam für das Dezimalsystem. Sie findet sich zweimal als Anfangsbuchstaben in den Gottheiten IVPPITER (109) und IVNO (56), die mit MINERVA die Kapitolinische Trias bilden, worüber ich eingehende Untersuchungen angestellt habe. Bezieht man sie auf die 5+1 Achsen, übernehmen die beiden Namen jeweils eine Radialeinheit je Achse.
2. Bereits aus den angegebenen ZS läßt sich die Zusammengehörigkeit von IUPPITER und IUNO erkenenn:
· Ihre
addierte ZS 165 = 15*11
ist wie die ZS 77
von MINERVA, der dritten Gottheit der Trias,
durch 11
teilbar. Die addierte ZS 242
entspricht der FS der 24
Begrenzungszahlen von 1-36. Liest man 242 als 24+2, erhält
man die Zahl 26 der Oktaederelemente: Der Oktaeder besteht aus drei horizontalen Ebenen
von je 8 Elementen und eine obere und untere
Ecke.
Die ZS 165 ist oben behandelt worden als Faktor der ZS+FS der Zahlen 1-30 + 1-36, als Summe der Zahlen 12-21 und FS der Zahlen 1-21.
· Aufgeteilt
in 10+9 und 5+6
verweisen die beiden ZS 109 und 56 in
chiastischer Stellung auf 10+6 Radialelemente
und 9+5 Durchmesserelemente
der beiden konzentrischen Tetraktyskreise.
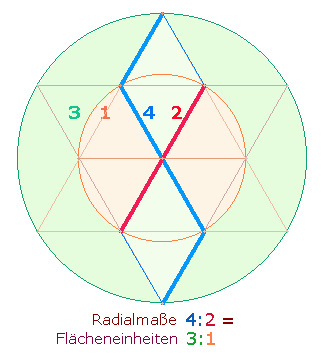
Gestützt wird diese Sichtweise 8 und 4 Buchstaben beider Namen. Denn die Zickzacklinie der DR enthält für die ganze DR und der hexagonalen Achse 4 und 2 Radialmaße, die bei Berücksichtigung des Doppelaspekts von DM- und Radialelemente zu verdoppeln sind:
|
|
Die entsprechenden Punktezahlen sind 3+5 = 8 und 4+6 = 10. Die Addition von 12 Radialmaßen und 18 Punkten ergibt 30. Unter Einbeziehung der Flächeneinheiten ergibt sich 5+6+2 = 13 für den hexagonalen und 9+10+6 = 25 für den Erweiterungsbereich. Die beiden Summen ihrerseits sind zusammensetzbar aus 7 Punkten + 6 Dreiecken des Hexagons und 13 Punkten + 12 Dreiecken des Hexagramms und geben somit wiederum das Kreisflächenverhältnis 1:3 wieder. 13*25 ist die Summe der Zahlen 1-25, denen das SATOR-Quadrat zugrunde liegt.
Die Summe von 30 Elementen einerseits und von 12 Maßeinheiten andererseits könnte Grundlage der zweifachen Zählung der Zahlen von 1-30 mit 10 Maßeinheiten und 1-36 von 12 Maßeinheiten sein.
3. IUPPITER wird demnach der äußere und IUNO der innere Kreis zugewiesen. In dieser Reihenfolge ist das Flächenverhältnis der beiden Kreise 3:1.
Auch die ZS beider Namenshälften sind durch 11 teilbar:
|
|
I |
V |
P |
P |
|
I |
V |
sm |
I |
T |
E |
R |
|
N |
O |
sm |
|
|
ZW |
9 |
20 |
15 |
15 |
|
9 |
20 |
88 |
9 |
19 |
5 |
17 |
|
13 |
14 |
77 |
165 |
Dem Flächenverhältnis 3:1 entsprechend enthält IUPPITER 3 und IUNO 1 Primzahl. Der trinitarische Aspekt erscheint darin deutlich: TER bedeutet dreimal, ist also auf drei Personen beziehbar, der ZW 13 des Buchstaben N faßt das Prinzip von 1 und 3 zusammen.
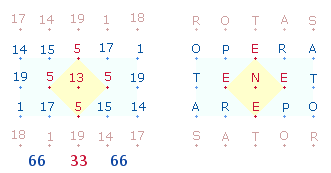
4. Die Zahl 165 ist auch die ZS der drei Mittelzeilen des SATOR-Quadrats:
|
|
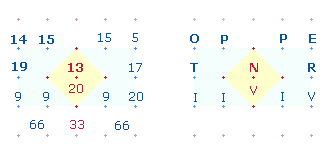
Der durchschnittliche ZW der 15 Buchstaben ist 11. 7 der 15 Buchstaben sind in den 12 Buchstaben von IVPPITER IVNO enthalten, ihre ZS ist 98. Die Differenz von 3 Buchstaben übernehmen für das Rautenquadrat der Mitte die Buchstaben VN = 20+13 = 33. Um die vertikalen Summen zu erhalten, müßten die Buchstaben etwa so angeordnet werden:
|
|
Lediglich die Buchstaben TOP der oberen linken Ecke und das Mittelpunkt-N stehen an ihren originalen Plätzen. Ihre ZS beträgt 61, das entspricht der ZS der Mittelzeile TENET. Damit die ZS 52 61 52 der drei Zeilen stimmen, müßte die Zahl 20 aufgeteilt werden in 3 und 5 in der oberen und unteren Zeile und zweimal 6 in der Mittelzeile.
Erstellt: April 2016