Die
Doppelsonne in de re publica I,15 und der Doppelkreis des Tetraktyssterns
A. I. Einleitung
V. Der Zahlenwert der Texteinheit
VI. Zweimal drei Namensbezeichnungen: die Metaebene
B. 6+6 Wörter; 2 weitere Modelle
I.
Einleitung
1. Die Stellung
des Menschen im Kosmos ist ein Thema, das Cicero zu Beginn seines
staatsphilosophischen Werks De re publica anschneidet
und am Ende seiner Ausführungen im Somnium Scipionis wieder
aufgreift. Tubero, einer der Gesprächsteilnehmer, fragt Scipio, was er von den
beiden Sonnen halte, die vor kurzem gesehen wurden. Wie das weitere Gespräch
zeigt, handelt es sich bei den DUO SOLES um eine
Sonnenfinsternis.
2. Das
Naturphänomen der Sonnenfinsternis mußte den gebildeten Teilnehmern des
Gesprächs als Bestätigung der kosmischen Ordnung erscheinen, die sich im
Dezimalsystem manifestiert.
3. In diesem
Beitrag geht es um den Zahlenwert (ZW) von DUO SOLES und weiteren
vier Wortgruppen, insgesamt 12 Wörtern, die Cicero für eine großartige
Zahlenkonstruktion einsetzt, um die Ordnung des Dezimalsystems darzustellen.
4.
Der Besucher dieser
Seite möge sich nicht durch die Fülle der Zahlen abschrecken lassen, wenn er
bedenkt, daß sie nur einen Bruchteil dessen darstellen, was im Bewußtsein
Ciceros präsent war.
II.
Die beiden Wörter
1.
Zerlegt man das Wort SOLES in die
symmetrischen Bestandteile SO-L-ES, erhält man
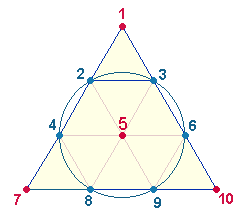
die ZW 32-11-23, zusammen 66. Die Umkehrzahlen 32 und 23 sind in der numerierten Tetraktys so enthalten, daß die Zahlen der 6 hexagonalen Kreislinienpunkte den Wert 32 und die Zahlen des
Mittelpunktes und der 3 Eckpunkte 23 ergeben:
|
|
Die Zahl 11 bezieht sich u.a. auf den Doppelaspekt von 5
Durchmesserelementen + 6 Radialelementen des Kreises. Indem 11 durch die Pluralendung –ES in die Mitte des Wortes
rückt, kann jeweils eine 1 (X-I) als Mittelpunkt und 2 und 3 als Numerierungen der 2*2 konzentrischen
Durchmesserelemente angesehen werden.
2. Der Rahmen
einer Tetraktys besteht aus 9 Punkten und 9 Linien, zusammen 18 Elementen. Der 18. Buchstabe ist das S. Die zwei S, die das Wort SOLES einrahmen, bedeuten demnach 2 Tetraktys, den Tetraktysstern und den Doppelkreis, innerhalb dessen sich
der Tetraktysstern befindet:
|
|
Die mittleren
drei Buchstaben OLE haben den ZW 30. Der Tetraktysrahmen wird gehalten durch die 3 Achsen des Hexagons mit je 5
Durchmesserelementen. Für zwei Tetraktys ergibt sich daher die doppelte Zahl 30.
Die
Gleichheit beider Tetraktys (V-EST-A) zeigt sich in 2*18 = 36 Rahmenelementen. Denn jede
Tetraktys besteht aus 3 Eckpunkten und 6 Hexagonalpunkten. Setzt man die
beiden addierten ZW 36+30
nebeneinander, kann man 6 Hexagonalpunkte für beide Tetraktys
und jeweils 3 Eckpunkte für jede unterscheiden.
Die beiden ZW erlauben das Verhältnis 6*(6:5). 6*11 = 66 beträgt die Summe der Zahlen 1-11.
Als 6+6 gelesen kennzeichnet der ZW von SOLES die 2*6 Kreislinienpunkte des Doppelkreises bzw. des
Tetraktyssterns.
3.
Der ZW von DUO SOLES ist 38+66 = 104 = 8*13. Da die
beiden Wörter aus 8 Buchstaben bestehen, ist der
durchschnittliche ZW 13. Die Zahl 13 bezieht sich sowohl auf die 13 Punkte des
Tetraktyssterns als auch auf das Verhältnis 1:3 des inneren
Kreis zum ganzen äußeren. Da die innere Fläche des größeren Kreises jedoch von
der Fläche des kleineren verdeckt wird, ergibt sich – nebeneinander
geschrieben, von innen nach außen – das Verhältnis 1:(1):2. Die Zahl 112 spielt denn
auch eine bedeutende Rolle im Dezimalsystem.
|
|
4. Das Produkt 8*13 verweist auf die 21 Elemente der Doppelraute (DR), die aus 13 Elementen des inneren Kreises und 8 Elementen des äußeren Kreisringes besteht:
5. Die beiden ZW
38 und 66 haben die Faktorenwerte
(FW) 21 und 16, zusammen 37. Die Zahlen 3 und 7 zeigen die Zusammensetzung der 10 Punkte der
Tetraktys, die aus 37 Elementen (10 Punkten, 9 Dreiecken,
18 Linien) besteht. Bei folgender Numerierung
des Doppelrautenrahmens entfällt der Wert 21 auf die 9 Rahmenelemente des inneren Kreises und der Wert 16 auf die 2*3 Elemente des Kreisringes:
Details zu DUO: die Zahlen 38 und
219
Rep. I,15
(1) Tum ILLE:
'visne igitur, quoniam et me quodam modo invitas et tui spem das, hoc primum, AFRICANE, videamus, ante quam veniunt alii,
quidnam sit DE ISTO ALTERO SOLE (27-28)
quod nuntiatum est in senatu? 33 (33)
(2) neque enim pauci neque leves sunt qui se DUO SOLES (42-43) vidisse dicant, ut non tam fides non habenda quam ratio quaerenda sit. 22 (55)
(3) hic SCIPIO: 'quam vellem PANAETIUM nostrum nobiscum haberemus! qui cum cetera tum haec caelestia vel studiosissime solet quaerere. 18 (18)
(4) sed ego, TUBERO – nam tecum aperte quod sentio loquar – non nimis adsentior in omni isto genere nostro illi familiari, qui quae vix coniectura qualia sint possumus suspicari, sic adfirmat ut oculis ea cernere videatur aut tractare plane manu. 38 (56)
(5) quo etiam sapientiorem SOCRATEM
soleo iudicare, qui omnem eius modi curam deposuerit, eaque quae de natura
quaererentur, aut maiora quam hominum ratio consequi possit, aut nihil omnino
ad vitam hominum adtinere dixerit. 32 (88)
Übersetzung:
(1) Da sagte jener
(=Tubero): "Willst du also, da du mich ja auf gewisse Weise einlädst und
mir Hoffnung auf dich machst, daß wir zuerst, Africanus, sehen wollen, bevor
andere (Gäste) kommen, was es denn mit dieser zweiten Sonne auf sich hat, was
im Senat gemeldet wurde?
(2) Denn es sind nicht wenige und nicht Leichtfertige, die
behaupten, zwei Sonnen gesehen zu haben, so daß es sich nicht mehr darum
handelt, daran zu zweifeln, sondern eine Erklärung zu suchen."
(3) Hier sagte Scipio:
"Wie wollte ich, wir hätten unseren Panaitios (griechischer Philosoph,
befreundet mit Scipio) bei uns! Der pflegt sowohl das Übrige, besonders aber
diese Dinge am Himmel aufs eifrigste zu untersuchen.
(4) Aber ich, Tubero –
denn mit dir will ich offen reden, was ich denke – , stimme auf diesem ganzen
Gebiet nicht allzusehr mit jenem unserem Freunde überein, der das, was wir mit
Mühe durch Vermutung in seiner Beschaffenheit ahnen können, so fest behauptet,
daß er es mit Augen zu schauen scheint oder einfach mit der Hand zu betasten.
(5) Für noch weiser als
ihn (freilich) pflege ich Sokrates zu halten, der jegliche Beschäftigung dieser
Art aufgegeben und gesagt hat, das, was über die Natur geforscht würde, sei
entweder größer, als daß es die Vernunft der Menschen erreichen könnte, oder
gehe das Leben der Menschen überhaupt nichts an".
1. Die ersten
beiden Sätze bestehen aus 33+22 = 55 Wörtern. Die Positionen der
Wörter altero sole und duo soles ergeben 55+85 = 140. Damit
verhält sich die Summe dieser 4 Wörter zu der Summe der
übrigen 51 Wörter 140*(1:10).
Das 4.
Wort SOLES steht an 43.
Stelle, dies entspricht dem ZW von SOL im
Singular.
2. Der ZW der 4 Wörter ist 115+104 = 219 = 3*73. Die Zahlenfolge 3-7-3 gibt die Zusammensetzung der 13 Punkte des Tetraktyssterns mit seinen 2 Dezimaldreiecken wieder: 3 Eckpunkte, 7 Hexagonalpunkte und weitere 3 Eckpunkte.
3.
Auch die 3 folgenden Sätze mit der Wortzahl 88 sind durch 11 teilbar. Die
gelb unterlegten Zahlen stehen in Übereinstimmung mit den Radialelementen des
Doppelkreises:
|
|
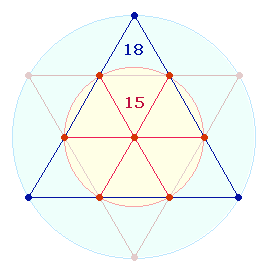
Die ersten beiden Sätze mit 22 und 33 Wörtern geben durch die Radialelemente (in doppelter Zählung) das
Flächeverhältnis 2:1 ,
die Zahl 88 (=5+3) das Flächenverhälntis 3:1 wieder.
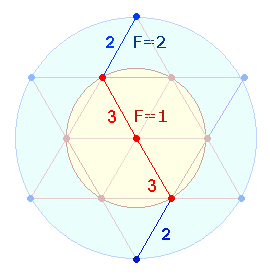
Ebenso als doppelte Zählung ist die Positionssumme 55 (altero
sole) zu verstehen; das dazugehörige Flächengröße ist 3.Die Positionssumme 85 (duo
soles) bezieht sich auf die Radialelemente in einfacher Zählung. Den Zahlen 8 + 5 (=3+2) entsprechen die Flächenverhältnisse 3:1 und 2:1. Die 2+3 Sätze
bezeichnen wiederum die Radialelemente von äußerem Kreisring und innerem Kreis.
Auch der ZW 115
für altero sole gibt durch das Produkt 5*23 die Radialelemente des
Doppelkreises wieder.
Die Sätze 1
und 5 bilden mit angrenzenden Wortzahlen 33+32 = 65 einen Rahmen von 5*13
Wörtern, der 3 Sätze mit 6*13 Wörtern einschließt.
4.
Die FW der 5
Buchstabensummen (143 = 11*13) ist 13+14+8+21+10 = 66. Der Wert 66 entspricht wiederum dem ZW von SOLES, das Differenzverhältnis von Faktorensumme (66) zu
Zahlensumme (66+77) ist 11*(6:7). Damit wird wiederum eine Teilung vorgenommen in 6 Punkte
(ohne Mittelpunkt) für den äußeren Kreisring und 7 Punkte für den inneren Kreis.
5. Schließlich
gibt die Buchstabenzahl selbst von DUO (3) SOLES (5) die
Radialelemente des inneren und des ganzen äußeren Kreises mit den Flächengrößen
1 und 3 wieder.
IV.
Alle vier Wörter
1. Die beiden
Adjektive ALTERO und DUO und die
beiden Substantive SOLE und SOLES bestehen
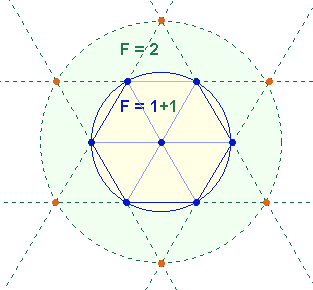
jeweils aus 9 Buchstaben (6+3, 4+5). Tatsächlich besteht Flächengleichheit zwischen dem
äußeren Kreisring (2) und dem zweimal zu zählenden inneren
Kreis (1+1).
Die Zahl 9
steht hier wohl vor allem für die 9
Durchmesserelemente des Doppelkreises. Die zweimal 9
Buchstaben lassen sich aber auch den 9
Punkten und 9 Linien des Tetraktysrahmens
und dem DR-Rahmen mit je 9 Elementen
zuordnen.
2.
Zum weiteren Vergleich der beiden Wortgruppen sind die Faktorensummen (FS) der Buchstaben der vier
Wörter heranzuziehen:
|
|
ZS |
FS |
Sm. |
|
ALTERO |
67 |
62 |
129 |
|
DUO |
38 |
22 |
60 |
|
Sm. |
105 |
84 |
189 |
|
|
21*(5:4) |
|
|
|
SOLE |
48 |
33 |
81 |
|
SOLES |
66 |
41 |
107 |
|
Sm. |
114 |
74 |
188 |
Die beiden Ergebnisse 189 und 188 sind zusammengehörige Konstitutivzahlen
für ihre Summe 377 = 29*13.
Die kombinierten ZW+FW-Werte für DUO (38+22) SOLES (66+41) ergeben 167. Diese Zahl hat eine
Beziehung zu den genannten Flächenverhältnissen 1:1:2,
insofern16*7 die Zahl 112 ergibt.
V. Der Zahlenwert der Texteinheit I,15
VI. Zweimal drei Namensbezeichnungen
1. Scipios
Bezugnahme auf den Philosophen Panaitios klingt etwas
eigenartig. Zuerst wünscht er sich, sein Freund könnte am Gespräch teilnehmen,
doch dann bezeichnet er ihn für das anstehende Thema als nicht ganz zuständig
und gibt stattdessen Sokrates den Vorzug. Es zeigt sich hier, daß der Text
gewissermaßen eine Metaebene besitzt. Es sollen zwei Namen ins Spiel gebracht
werden, die durch ihre Zahlenwerte einem höhergeordneten Ziel dienen.
2. Der Text
besteht aus zwei Dialogteilen. Jeder wird durch zwei Wörter ohne Verb
eingeleitet: TUM (51>FW 20) ILLE (36>10) – HIC (20>9) SCIPIO (68>21). Man erkennt
aus den ZW 87+88 = 175 und FW 30+30 = 60 die enge
thematische Bezogenheit der beiden Gesprächspartner: und. Die Summe 235 zeigt die Radialelemente des Doppelkreises in doppelter Zählung
zuerst als Teilzahlen (von außen nach innen), dann als Summe.
3. In einer
weiteren Parallele spricht jeder Gesprächspartner den anderen an: ILLE – AFRICANE (55), SCIPIO – TUBERO (77). Durch das ZW-Verhältnis 11*(5:7) stehen beide
Gesprächspartner im Dienst einer gemeinsamen geistigen Aufgabe.
4. Indem SCIPIO dem TUBERO seine wahre
Meinung über Panaitios anvertraut,
ordnet er diesen der Seite des TUBERO zu, so daß
für ihn selbst Sokrates vorbehalten
bleibt.
Die Buchstaben der beiden Namen im Akkusativ PANAETIUM (95) und SOCRATEM (89) haben dieselbe Faktorensumme (FS) 69 = 3*23. Die Zahl 69 ist der ZW des Wortes SATOR – Schöpfergott. Durch ihre geistige Tätigkeit sind beide Philosophen
mit der Weisheit Gottes verbunden.
Panaitios und Sokrates ergänzen
sich darin, daß ihr gemeinsamer ZW 184 durch 23 teilbar ist wie jede einzelne FS. Das Verhältnis von ZW zu FS ist nun 23*(8:6) = 46*(4:3). Durch die Zahlen 4+3 repräsentieren beide Philosophen die Fülle der
göttlichen Weisheit. Die Zahl 46 ist nicht nur die FS der Zahlen 1-10, sondern in der Aufteilung 4+6 stellt sie 4 Linien und 6 Punkte der 10 Radialelemente des Doppelkreises
dar.
5.
Die grundlegende Bedeutung des Produktes 2*3 liegt in der doppelten Anzahl der Radialelemente. Weitere analoge
Bedeutungen lassen sich aus der nachfolgenden Tabelle erkennen (Die erste Zeile
ist spiegelbildlich von rechts nach links zu denken):
|
Radius |
|
ZW |
|
ZW |
|
ZW |
Sm. |
Bu. |
|
links |
ILLE |
36 |
AFRICANE |
55 |
PANAETIUM |
36 |
186 |
21 |
|
rechts |
SCIPIO |
68 |
TUBERO |
77 |
SOCRATEM |
89 |
234 |
20 |
|
Bu./Sm. |
10 |
104 |
14 |
132 |
17 |
184 |
420 |
41 |
|
Faktoren |
|
8*13 |
|
12*11 |
|
8*23 |
|
|
|
|
186:234
= 6*(31:39) |
|||||||
Die Verhältniszahlen 31:39 (=3*13) spiegeln in zweifacher Weise die
Flächenverhältnisse des Doppelkreises 1:2 und 1:3 wider. Durch Addition der
Einzelziffern (3+1, 3+1+3) erhält man
4+7, durch Addition der Primzahlfaktoren 31+16 = 47. Die Summe der zweistelligen Faktoren der Teilergebnisse
11+13+23 beträgt
ebenfalls 47. Die drei Teilergebnisse sind jeweils durch 4 teilbar.
Die mittlere und rechte Summe ist jeweils durch 8 teilbar.
Die
Buchstabenzahl 21+20 = 41 verweist auf die 41 Elemente des Doppelrautenkreuzes. Die 7 Punkte einer
Doppelraute gliedern sich in 3+1+3 und geben
damit die grundlegenden Flächenverhältnisse wieder. Den 3 Radialelemente eines
Kreises entsprechen hier 3 Längspunkte, auf denen die 6 Namen
plaziert werden können:
|
|
Das Grundmuster 1:2 und 1:3 (mit Umkehrungen) zeigt sich auch in der Tetraktys mit 1+2 Eckpunkten
und 1
Mittelpunkt + 3 Eckpunkte.
6. Die Krönung
eines gematrischen Unternehmens besteht für den lateinischen Autor darin,
Wörter oder Buchstaben einer geometrischen Figur zuzuordnen, die für das
Dezimalsystem von Bedeutung ist. Die 41 Buchstaben
sollen nun in ein Doppelrautenkreuz eingetragen werden. Die stehende DR soll 21 Buchstaben enthalten, die liegende 20 (=ohne
Mittelpunkt). Die Buchstabenzahl jedes Wortes dient als Wegweisung, in welcher
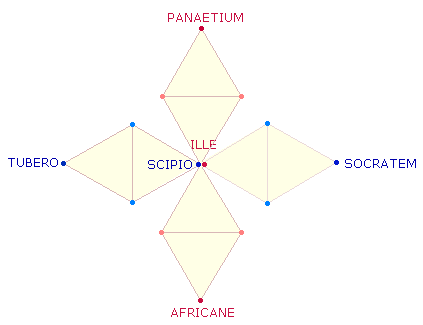
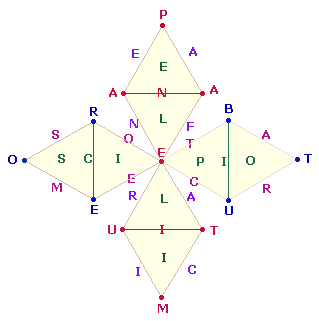
Reihenfolge und an welcher Stelle die Zuordnung vorgenommen werden soll:
Das Wort ILLE besetzt (von unten nach oben) die 4 Dreiecke. Die 8 Buchstaben von AFRICANE werden in 8-förmiger Umfahrung auf den Linien
eingetragen. Die 9 Buchstaben von PANAETIUM werden von oben nach unten den 7 Punkten + 2 Querlinien zugeordnet.
Die liegende
DR beginnt analog zur stehenden mit SCIPIO und der
Belegung der 6 Elemente des umrahmten Mittelteils.
Das Wort TUBERO besetzt die 6 Punkte und SOCRATEM die 8 Linien. Nach Möglichkeit soll
am Ende der Ausgangspunkt der Buchstabenbesetzung wieder erreicht werden:
|
|
7. Die Besetzung
eines geometrischen Modells mit Buchstaben kann nur dann als erfolgreich
gelten, wenn sich passende Zahlenverhältnisse ergeben. Im vorliegenden Fall
führen die 2*6 = 12 Buchstaben
der beiden umrahmten Mittelteile zum ZW 58+68 = 126 = 3*42, das
Verhältnis zum ZW der übrigen 29 Buchstaben beträgt demnach 42*(3:7).
Die ZS der 2*8 = 16 Rahmenlinien
beträgt 144, das bedeutet einen durchschnittlichen ZW von 9. Dasselbe gilt für die 4 Querlinien
mit der ZS 36. Den 20 Linien stehen
also 13 Punkte + 8 Dreiecke
gegenüber. Dem Buchstabenverhältnis 20:21 entspricht
das ZW-Verhältnis 180:240 = 60*(3:4).
Erstellt: März
2006