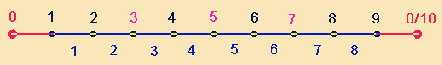Entwicklung des Dezimalsystems
X. Die Doppelraute (II)
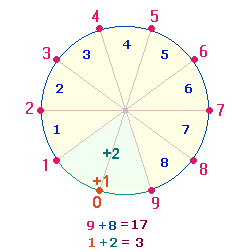
a) Vergleich von
Strecke und Doppelraute
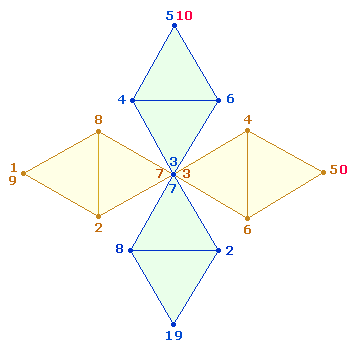
b)
Doppelte Numerierung der Doppelraute
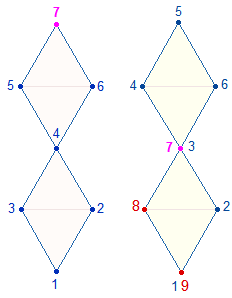
c)
Nachweis der 3 Stellen in 10. Position
|
|
1. Die beiden Modelle
des Strecken- und Kreisformats (s.Kap.IX) haben die
gegenseitige Bedingtheit von Begrenzungspunkten und Maßeinheiten deutlich
gemacht. Der Punkt ist
einerseits unentbehrlich als Kreis- und Symmetriemittelpunkt vermehrbarer
Durchmesserpunkte, die 10-Zahl der Maßeinheiten aber
entscheidend für die Zyklik des
Dezimalsystems.
2. Die beiden
Modelle sind sinnvolle Lösungen für den Doppelaspekt der 9 DM-Elemente und der 2*5 Radialelemente, unter Einbeziehung
der 0. Auch wenn im Kreisformat die 10 neben der 0 stehen könnte, ist die
Aufgabenteilung in Kreisformat (0-9) und Streckenformat (0-10) befriedigender.
3.
Will man die 0 zu einem
zählbaren Element machen, ist jedes Modell doppelt zu zählen. Man berechnet die
Summe der jeweiligen Zahlenreihen:
|
|
|
Kr.Modell |
Str.Modell |
Sm. |
FW |
||
|
0=0 |
P |
0-9 |
45 |
0-10 |
55 |
100 |
|
|
|
L |
1-10 |
55 |
1-10 |
55 |
110 |
|
|
0=1 |
P |
1-10 |
55 |
1-11 |
66 |
121 |
|
|
|
L |
1-10 |
55 |
1-10 |
55 |
110 |
|
|
Sm. |
|
|
210 |
|
231 |
441 |
20 |
|
FW |
|
|
17 |
|
21 |
38 |
21 |
|
|
|
|
|
|
|
|
41 |
Die FW 17 und 21 stellen das interne Verhältnis
von FW und ZW der nominalen Endung VS dar: ZW =
20+18 = 38, FW = 9+8 = 17; 38-17 = 21.
Der ZW-Rest 21 spielt in DEVS (47)– Gott eine besondere Rolle. Teilt man die 4 Buchstaben
in 2+2, setzt sich die FS aus 9+17 = 26 zusammen. Aus 26 Elementen besteht der Oktaeder. Der ZW-Rest
stellt jedoch die – gleich zu behandelnden – 21 Zahlzeichen
der doppelten DR-Numerierung dar. Die Zahlen 9+17 (=9+8) sind
symmetrische Entsprechungen zu 1+(1+2), die das
trinitarische Verhältnis 1:3 bilden.
4. Strecken- und
Kreismodell sind keine natürlichen, sondern gedankliche Konstruktionen, da ihre
Größenordnung von der Zahl der gewählten Begrenzungspunkte abhängen. Die
Doppelraute (DR) aber geht aus einer natürlichen geometrischen Konstruktion
hervor, die neben Punkte und Linien auch Dreiecke enthalten, die zur Bedeutung
der Figur dazugehören: Die 7 Punkte der DR umgrenzen 4 Dreiecke und bilden zusammen 11 Elemente,
die durch 10 Linien begrenzt werden. Die 4 Dreiecke übernehmen gewissermaßen die Funktion von 4 Punkten des Streckenmodells.
b) Doppelte
Numerierung der Doppelraute
1. Im
Streckenmodell ist die Zahl der Maßeinheiten abhängig von der Zahl der Punkte.
In der DR sind 10 Maßeinheiten vorgegeben. Zwar gehören
die 4 Dreiecksfächen (F) zahlenmäßig zu den Punkten, aber
diese sollten so numeriert werden, daß sie den 10 Maßeinheiten
(Linien) entsprechen. Dies ist erreichbar, wenn man die 7 Punkte ab der Zahl 1 numeriert, bis man den ersten Punkt
wieder erreicht und diesen mit 9 bezeichnet.
2.
Nun bleibt noch die Aufgabe, in doppelter Numerierung die
9 DM- und 10 Radialelemente darzustellen.
Dies bereitet keine Schwierigkeit, wenn man weiß, daß man aus 2 in einander
verschränkten DR die dreidimensionale Figur des Oktaeder bilden kann:
Man biegt jeweils die Spitze mit der 1 nach hinten
und vereinigt sie mit der gegenüberliegenden. Auf diese Weise gewinnt man für
die Numerierung eine neue Position. Der DR-Verschränkung gemäß ist die Form
eines Achsenkreuzes:
|
|
3.
Das Oktaeder-Modell besteht also aus zwei geschlossenen
Kreisen. Die 10. Position wird einmal durch 10 und einmal –
wie im Kreismodell – durch 0 besetzt. Betrachtet man die
Zahl 10 als aus 2 Ziffern bestehend, lassen sich für das Strecken- und
Kreismodell einerseits und für die beiden DR-Kreise folgende Verhältnisse der Null-Zahlen feststellen:
|
|
DM-E. |
Rad.E. |
|
|
|
9 |
10 |
Verhältnis
|
|
Str./Kr.-Mod. |
0 |
0-10 |
1:3 |
|
2 DR |
0 |
10 |
1:2 |
Die beiden Numerierungen sind eine Entsprechung zum Kreismodell: 10 Maßeinheiten
erfordern als ersten Begrenzungspunkt die 0:
|
|
4. Im Gegensatz
zum Strecken- und Kreismodell beginnt die Numerierung der beiden DR mit der
Zahl 1 und endet mit 10 bzw. 0. Läßt man die erste (hier vertikale) DR mit 10 und die zweite mit 0 enden, bietet sich folgende Deutung an: Die Verbindung
der 1 und der 0 bedeutet, daß die Gesetze der
Schöpfung (=Naturgesetze) ein Abbild des dreifaltigen Gottes sind und von
seiner unsichtbaren Kraft im Dasein gehalten werden. Die zweite DR führt – entsprechend
der Bildung des Oktaeders – die Erschaffung des Kosmos zu ihrer Vollendung. Die
0 zeigt an, daß die Schöpfung zu ihrem Schöpfer
zurückstrebt, indem sie sein Lob verkündet.
Wenn man der ersten DR die 0 und der zweiten die 10 zuordnet,
ändert sich die Betrachtungsweise dahingehend, daß – wie beim Streckenmodell –
die zur 0 zurückkehrenden Zahlen 1-9 die Idee des
Dezimalsystems und die 10 ihre endliche Verwirklichung
darstellt. Ich selbst ziehe die Folge 0-10 der Folge 10-0 vor.
5. Die 5. und 10. Position der beiden DR zeigt eine bemerkenswerte
Variabilität: Die 4 Positionen enthalten nur 3 Grundzahlen, aber 5 Stellen.
Die 8-förmige
Numerierung und Rückkehr zum 1. Punkt erbringt eine Erweiterung der Grundzahlen
von 7 auf 9:
|
|
Die 10 Positionen werden also in den drei Schritten 7+2+1 erreicht. Rechnet man für die
Zahl 10 zwei Stellen, lautet die Variante 7+2+2. Das Verhältnis von normaler
zu erweiterter Numerierung beträgt nun 14:7. Damit entspricht die Zahl der 20 Positionen +
1 Stelle 21
Begrenzungspunkten für 20
Maßeinheiten.
Der Variabilität der zwei 10. Positionen
entsprechend lassen sich 3 Zahlenwerte für die 2*(3*2) vertikalen Positionen
bilden: 11 Grundzahlen, 12 Positionen und 13 Stellen.
Fügt man die 4*2 horizontalen Positionen hinzu, erhält man die
Gesamtzahlen 19, 20, 21. Die ZS der 6 Zahlen ist 96, die FS die Umkehrung 69.
Im Oktaeder
schrumpfen die 14 anfänglichen Punkte der beiden
Doppelrauten auf 6 Ecken. Verbindet man mit den 6 Ecken mit den 21 Zahlzeichen, erhält man die beiden
Zahlen 621 und 216. Die ZW/FW-Verrechnung
liefert folgendes Ergebnis:
|
|
ZW |
FW |
Sm. |
FW |
|
|
621 |
32 |
|
|
|
|
216 |
15 |
|
|
|
Sm. |
837 |
47 |
884 |
34 |
|
FW |
40 |
47 |
87 |
32 |
|
Sm. |
|
66 |
||
Die Zahlen 34 und 32 lassen sich auf den Oktaeder und das Achsenkreuz
9 beziehen: Je eine Oktaederhälfte besteht aus 17
Elementen.Von der unteren zur oberen Ecke sind es 5 Elemente und bis zum letzten vor der unteren Ecke weitere 3. Da man 4 Bahnen umfahren kann, sind es
zusammen 4*8 = 32 Elemente. Das Achsenkreuz 9 zählt je Achse 17 Punkte und 16 Linien. Die Zahl 66 ist der ZW von SPQR.
6. Da jede DR
aus 21 Elementen besteht,
verhalten sich die Elemente zweier Doppelrauten zu den 19 (sichtbaren) + 2
(unsichtbaren) Zahlzeichen wie 2:1. Die
Addition 42+21 = 63 ergibt denselben ZW wie das Wort VESTA, dessen Buchstaben VS ein internes Verhältnis zwischen FW
und ZW-Rest von 42:21 bewirken.
Nimmt man an, daß die doppelte DR-Numerierung und der Oktaeder ontologische Relevanz für das Dezimalsystem besitzen, lassen sich drei ZW und deren FW ermitteln.
Wenn man die 26 Oktaederelemente um 1 Volumen = 27 Elemente erweitert, ergibt sich
folgende Doppelrechnung:
|
|
ZW |
FW |
ZW |
FW |
Sm |
FW |
|
Okt. |
26 |
15 |
27 |
9 |
|
|
|
2 DR |
42 |
12 |
42 |
12 |
|
|
|
Num. |
21 |
10 |
21 |
10 |
|
|
|
Sm. |
89 |
37 |
90 |
31 |
179 |
179 |
|
FW |
89 |
|
13 |
|
102 |
22 |
|
|
201 |
|||||
Die Umkehrwerte 102 und 201 zeigen einen Bezug zu den ZW des SATOR-Quadrats.
Die Primzahlen 37 und 31 ergeben
zusammen 68, das ist die Summe der numerierten drei Seiten der Tetraktys, wenn man
jede Seite getrennt zählt. Catull hat 37 und 31 als Buchstabenzahlen in den bekannten Distichen c. 85 und c. 93 verwendet. Natürlich kann er die Bedeutung der
beiden Zahlen auch aus einem anderen Zusammenhang bezogen
haben.
c) Nachweis der 3 Stellen in 10. Position
Die
Erweiterung der 7 Punkte der DR um die Positionen 8, 9 und besonders Position 10 mit ihren 3 Stellen, aber nur 1 Grundzahl,
gehört offensichtlich zu den tieferen Geheimnissen des Dezimalsystems. Für die 2+3 Stellen der 5.+10. Position
sollen 4 Nachweise erbracht werden:
1. Als ich daran
ging, im Rahmen meiner Ovid-Lektüre den strukturellen Platz der Geschichte von
Dädalus und Ikarus innerhalb des Gesamtplanes zu ermitteln, fand ich heraus,
daß der Mittelteil der Metamorphosen aus 721+722 Versen besteht, wobei die Dädalus-Sage den Abschluß der ersten Hälfte des
Werkes bildet. Ovid unterlegte vermutlich den 15 Büchern der Metamorphosen
Strukturvorstellungen des Oktaeders. Allerdings bin ich dieser Vermutung über
den Befund des Mittelteils hinaus nicht weiter nachgegangen.
2. Die 4. Ekloge Vergils besteht aus 63 Versen,
entsprechend den 3 Doppelrauten des Tetraktyssterns zu je 21 Elementen. Die Gliederung des Gedichts weist alle Merkmale der Doppelraute
auf: Gemäß den 9 Durchmesserelementen haben die
Versgruppen folgende konzentrische Anordnung:
3+7 || 7+8 || 11 || 9+7 || 7+4
Die Verse 1-3 und 60-63 sind – unter
konzentrischem Gesichtspunkt – folgenden Ziffern und Stellen zuzuordnen:
Der Zuwachs gegenüber der doppelten Numerierung von 1-7 (56) beträgt 0+9+8 = 17; 8+9+10=17+10 = 27; 17+27 = 44.
Die ZW des 1. und 63. Verses sind 321+342 = 663.= 3*13*17 = FW 33. Die FW der beiden
Zahlen sind 110+27 = 137. Die
Addition 33+137 ergibt 170= 17*10. Addiert man das Produkt, erhält man die Zahl 27. Die Zahl 110 kann man als
zweifache Addition der 10.+5. Position
ansehen: 0|5+10|5 = 110. Durch weitere FW-Ermittlung ergibt sich: 663+137 = 800 = FW 20; 170 = FW 24. Durch
Addition der beiden neuen FW erhält man 44.
Der 62. Vers hat den ZW 404, der bereits
die Zahl 44 enthält und den FW 10|5 hat. Setzt man in Umkehrung die 5. und 10. Position nebeneinander, erhält man 5|0+5|10 = 560 = 10*56. Die ZW der Verse 62 und 63 ergeben 404+324 = 728 = 13*56 = FW 26. Die FW 105+27 = 132 = 11*12 führen zu FW 18 und zusammen mit FW 26 wieder zu 44. Das Produkt 11*12 kann die 2+3 Stellen der 5.+10. Position
bedeuten. Auch die Addition der Einzelziffern der drei ZW 321,342,404 ergibt 6+17 = 23.
Die nebeneinander gesetzten Werte der 5. und 10. Position betragen mit Umkehrung 110+560
= 670 = 10*67. Denselben Wert als
4-stellige Zahl ergibt die Addition der 3 ZW: 321+404+342 = 1067.
Daß die ZW 404 + 342 zusammengehören, zeigt sich
in der Addition ihrer FW 105+27 = 132 und im
Vergleich mit dem FW 110 des ZW 321. Das Verhältnis beider FW ist 22*(6:5).
3.
Die nächste Argumentation ist kein Nachweis im strengen Sinne,
aber sie ist einleuchtend. Wenn die 4 DR-Enden zur Bildung eines Oktaeders nach
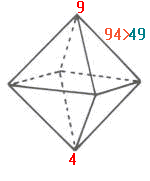
oben zusammengeführt werden, bilden sie mit 4*2 = 8 Positionen +1 Nullstelle die obere Spitze des Oktaeders und der Mittelpunkt mit 4 Positionen die untere:
|
|
Von oben nach unten liest man 94. Kehrt man
die obere und untere Spitze um, ist die Lesefolge von oben nach unten 49. Dies wäre nichts Besonderes, wenn der Faktorenwert von 94 nicht ebenso die Umkehrung 49 wäre. Die
Addition beider Werte ist 143 = 11*13. Nun besteht
ein Oktaeder aus einer Abfolge von Rauten
und sanduhrartigen Doppeldreiecken; erstere bestehen aus 11, letztere aus 13 Elementen.
Man kann die Rechnung mit den FW weiterführen:
|
|
|
|
sm |
|
Zahl |
94 |
49 |
143 |
|
FW |
49 |
14 |
63 |
|
sm |
143 |
63 |
206 |
Die Werte sind so zu
verstehen: Der Tetraktysstern besteht aus 49
Elementen, fügt man den FW 14 hinzu, ergibt
sich 63 = 3*21, d.h. die Elemente der drei
Doppelrauten. Teilt man die Summe 206
in 20+6 auf, erhält man die 26 Elemente des Oktaeders: 12 Kanten + 8 Flächen und 6 Ecken.
Die Einzelziffern der Zahl 94 = 2*47 lassen sich interpretieren als zweimal 4 Dreiecke und 7
Punkte in der Doppelraute und als 4 Dreiecke
und 9 Punktepositionen bei schleifenförmiger
Numerierung. 9+4 ist auch auf zwei
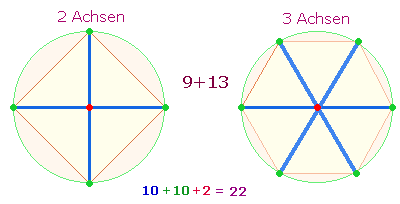
entscheidende Achsenkreuze anzuwenden:
|
|
Die beiden Achsenfiguren enthalten
10 Maßeinheiten. Das hexagonale Achsenkreuz
enthält 4 Maßeinheiten mehr als das
horizontal-vertikale Achsenkreuz.
4. Wie die letzte Tabelle der
Faktorenwerte zeigt, ist die fortlaufende Faktorensumme für 100 die Primzahl 2281, deren ersten beiden Ziffern sich auf die 2*2 Positionen des DR-Mittelpunktes beziehen, während die
letzten beiden auf 4*2 = 8 Positionen +
1 zusätzliche 0-Stelle der Zahl 10 verweisen.
Der Bezug der Zahl 100 zur doppelten DR-Numerierung ist
zweifach:
Erstens, die
Vereinigung der beiden DR-Spitzen ermöglicht die Nurmerierung von 10
Positionen. Der Kreisform der 2 DR und des Oktaeders gemäß ist die Quadratform:
Der Verschränkung beider DR zur Oktaederbildung entspricht die Multiplikation
von 10*10 Positionen.
Zweitens, die
Zahl 100 setzt sich
aus 10 und 0 zusammen, wenn sich die 0 der 2. DR der 10 der 1. DR anschließt, bzw. wenn die Zahl 10 vor die 0 tritt, z.B. im Kreismodell.
Erstellt: August 2001
Überarbeitet: September 2005
Letzte Änderung:
2016