Umkehrungen
dreistelliger Zahlen
IV. Umkehrungen der Zahlen 12, 13, 14,
23
1.
Es gibt 9
dreistellige Zahlenpaare, deren Umkehrungen auch Umkehrungen ihrer Faktoren
sind. Zwei Zahlenpaare (144, 169) betreffen die Quadratzahlen von 12 und 13. Dreimal jeweils zwei Zahlenpaare verbinden die
Zahl 12 mit 13, 14 und 23. Die Zahl 13 verbindet sich nur einmal mit 23 und keinmal mit 14, da Multiplikationen in die
Vierstelligkeit hineinreichen:
|
|
|
Fkt. |
FW |
|
Fkt. |
FW |
sm |
Fkt. |
|
12² |
144 |
12*12 |
14 |
441 |
21*21 |
20 |
585 |
45*13 |
|
13² |
169 |
13*13 |
26 |
961 |
31*31 |
62 |
1130 |
10*113 |
|
12,13 |
156 |
12*13 |
20 |
651 |
21*31 |
41 |
807 |
3*269 |
|
12,13 |
273 |
21*13 |
23 |
372 |
12*31 |
38 |
645 |
15*43 |
|
12,14 |
168 |
12*14 |
16 |
861 |
21*41 |
51 |
1029 |
3*7³ |
|
12,14 |
294 |
14*21 |
19 |
492 |
12*41 |
48 |
786 |
6*131 |
|
12,23 |
276 |
12*23 |
30 |
672 |
21*32 |
20 |
948 |
12*79 |
|
12,23 |
384 |
12*32 |
17 |
483 |
21*23 |
33 |
867 |
3*17² |
|
13,23 |
299 |
13*23 |
36 |
992 |
31*32 |
41 |
1291 |
|
|
|
2163 |
121+164 |
201 |
5925 |
191+283 |
354 |
8088 |
|
|
2163
= 21*103; 5925= 25*237 = 125*79; 8088
= 24*337 |
||||||||
|
121+164+191+283
= 759 = 69*11 = 3*11*23; 201+354
= 555 |
||||||||
2.
Die Quersummen der zweistelligen Faktoren beträgt jeweils 69, daher beträgt ihre Summe 69*11.
Die doppelte Umkehrung der Ausgangsfaktoren
12+21 usw. bewirkt doppelte
Teilbarkeit durch 11,
also einmal 33*44 (13+31) und zweimal 33*55 (14+41;
23+32) mit dem
Ergebnis 11*11*(12+15+15) = 11*11*42 = 363*14 = 5082. Die Summe der übrigen drei
Zahlenpaare beträgt 3006 = 18*167. Die Ziffern 3 und 6 kennzeichnen den
Tetraktysrahmen aus 6 hexagonalen und 3 Erweiterungslinien. Dasselbe gilt für die 9 Dreiecksflächen der
Tetraktys.
Die ZS 8088 und die FS
555 ergeben zusammen 8643 = 3*43*67. Die Einzelziffern der
Primzahlen 43
und 67 sind komplementär und
ergänzen sich zu jeweils 10. Sie lassen sich auf den Tetraktysrahmen beziehen, dessen einzelne
Seite sich aus 4 Punkten
+ 3 Linien zusammensetzt, aber
nur aus 6
Elementen besteht, wenn man die 18 Elemente aus 9 Punkten und 9 Linien durch 3 teilt:
|
|
Der Faktor 337 ist aus zwei
der 9 Zahlen, 169+168, zusammengesetzt. Mehr zur Bedeutung der
Zahl 337.
3.
Die 9
Zahlen und ihre Umkehrungen lassen sich auf drei geometrischen Figuren
anordnen: den 9
Linien des Tetraktysrahmens, den 9 Dreiecksflächen der
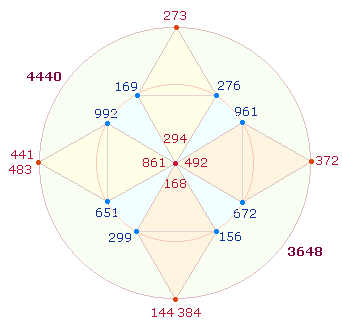
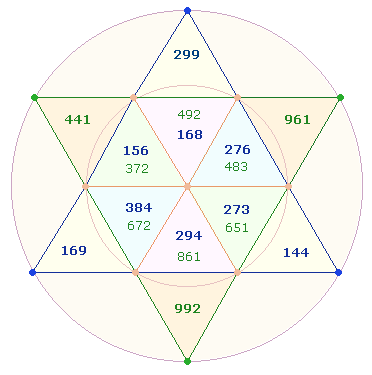
Tetraktys und den Punkten der Doppelraute (DR). Die folgende Grafik zeigt die 2*9 Zahlen im DR-Kreuz: Die Anordnung
wird vom untersten Punkt aus in 8-förmiger Schleife durchgeführt, die der
Umkehrungen von der linken Raute aus. Die 9 Zahlen in aufsteigender
Reihenfolge sind: 144, 156,
168, 169, 273, 276, 294, 299, 384:
|
|
Den Mittelpunkt bilden die beiden Zahlenpaare mit den
Zahlen 12 und 14. Ihre ZS ist 15*11*11 = 1815. Die ZS der Eckpunkte beträgt 2097 = 3*13*23, die
der Querpunkte 4176 = 12*12*29.
Das ZS-Verhältnis
der unteren und rechten zur linken und oberen Raute beträgt 3648:4440 = 24*(152:185). Die Faktorenwerte (FW) beider Summen sind 34 und 51
und haben somit das Verhältnis 17*(2:3). Durch Winkelverschiebung entsteht aus dem DR-Kreuz
ein Oktogon.
Das Verhältnis der roten zu den blauen Zahlen ist 3912:4176 = 24*(163:174).
Die FW beider Summen sind 172 und 43, das
FW-Verhältnis beträgt 43*(4:1).
4.
Das DR-Kreuz läßt sich zu einem Oktaeder zusammenfügen:
|
|
Ein Oktaeder besteht aus zwei
gegeneinander gewendeten Paramiden: eine stellt die Umkehrung der anderen dar.
In den beiden Hälften des Oktaeders haben die Umkehrzahlen eine logische
Ensprechung. Die Ergebnisse der neun Umkehrzahlen haben daher eine innere
Beziehung zu den Eigenschaften des Oktaeders.
Ein Oktaeder ist also als ganzer und in beiden
Hälften zu betrachten:
– Als ganzer besteht er aus 6 Ecken, 12 Kanten und 8
Flächen, zusammen 26 Elementen. Faßt man Ecken und Flächen zusammen, so zeigt sich eine
Übereinstimmung mit den Faktoren 14 und 12
der dreistelligen Umkehrzahlen. Das Ergebnis 14*12 = 168 ist auch durch die Aufteilung des Gesamtergebnisses 8088 in 80+88 erkennbar.
Die dreimalige 8 hat ihren Sinn darin, daß die 9 Durchmesserelemente, die
sich in der Doppelraute dreimal finden bzw. in jeder der drei Doppelrauten, durch die Vereinigung der
äußeren Punkte auf 8 reduzieren:
|
|
Weiterhin besteht die Mittelbasis der beiden
Oktaederhälften aus 8 Elementen sowie die darüber und untere Umlaufbahn aus
4 Kanten und 4 Flächen.
Eine Raute verbindet jeweils die beiden
Oktaederhälften. Ihr Rahmen besteht aus 8 Elementen, die 3
Binnenelemente umschließen. Das Doppeldreieck, das über die Spitze einer
Oktaederhälfte führt, besteht aus 13 Elementen, sodaß die
Elemente dieser beiden Grundfiguren (11+13) ebenfalls den
Teilungsfaktor 24 der Summe 8088 begründen.
– Eine
Oktaederhälfte besteht aus 8 Elementen der Mittelbasis, der Umlaufbahn aus 4
Kanten und 4 Flächen und der Spitze, somit aus 17
Elementen. Weitere 9 Elemente ergänzen die erste Oktaederhälfte zur
Gesamtfigur. Als zwei eigenständige Hälften sind 2*17 Elemente zu
zählen.
5.
Unter dem Gesichtspunkt dieser Eigenschaften des Oktaeders sind die
einzelnen Summen näher zu untersuchen. Dabei spielen die Faktorensummen
(FS) eine bedeutende Rolle.
Die beiden pyramidalen Aufbauten werden durch die
Zahlen der 4 äußeren Punkte (oben) und des Mittelpunktes (unten), die Mittelbasis
durch die Zahlen der Querpunkte vertreten. Es interessieren zunächst die ZS+FS der drei
Zahlengruppen:
|
|
oben |
Mitte |
unten |
|
|
Zahl |
2097 |
4176 |
1815 |
8088 |
|
FW |
39 |
43 |
30 |
112 |
|
|
|
|
|
8200 |
Die Zahl 112
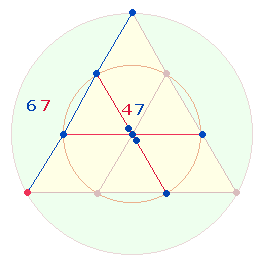
zeigt durch die Einzelziffern ihres Produkts 16*7 ihre Bedeutung
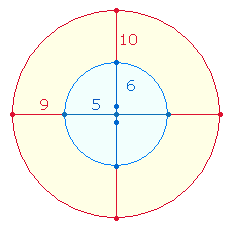
hinsichtlich der beiden Tetraktyskreise, deren Fläche das Verhältnis 1:3
haben: Aus Mittelpunkt und 6
Kreislinienpunkten besteht das Hexagon, durch seine Erweiterung zum Hexagramm
kommen 6 Punkte hinzu, die um einen Mittelpunkt erhöht werden
müssen, um einen zweiten Kreis zu bilden. Die Primzahl 167 wurde bereits oben ermittelt.
Einer Oktaederhälfte können ZS+FS 4100
zuteilen. Neben den beiden genannten geometrischen Figuren aus 11
und 13 Elementen kommt noch die "Fischfigur" aus 17
Elementen hinzu:
|
|
Die DR selbst
besteht aus 21 Elementen, sodaß sich die Gesamtsumme 62 ergibt. Diese kommt auch durch die Basisfaktoren der 9
dreistelligen Zahlenpaaren zustande: 12+13+14+23 = 62.
Der FW
von 4100 setzt sich aus der Umkehrung 41+14 = 55 zusammen.
6.
Zur Ermittlung der beiden Hälften ist die ZS der gemeinsamen Mittelbasis 4176 = 24*174 zweimal zu addieren:
|
|
oben |
unten |
sm |
|
|
2097 |
1815 |
|
|
|
4176 |
4176 |
|
|
|
6273 |
5991 |
12264 |
|
FW |
64 |
2000 |
2064 |
|
6273
= 9*17*41 |
14328 |
||
|
5991
= 3*1997; 2064 = 24*86 >54 |
|||
|
12264 = 24*7*73 >89 |
|||
|
14328
= 24*597= 72*199 >211 |
|||
Die Produktzahlen 9*17 bezeichnen die 9+17 Elemente des Oktaeders. Indem sich 17
aus 9+8 zusammensetzt und 9 und 8 die
Komplementärzahlen zu 1 und 2 sind, stellt 9:17 das
Komplementärverhältnis zu 1:3 dar.
Die Zahl 41 steht für die Zahl der Elemente eines DR-Kreuzes.
Die Faktoren der ZS 12264
verbinden die Figuren der Tetraktys und der DR: 7
hexagonale Punkte und 7+3 Tetraktyspunkte geben das Kreisflächenverhältnis 1:3 wieder. Das Produkt 7*73 = 511 weist auf
die DR mit 5
hexagonalen und 2
Erweiterungspunkten hin, der Faktor 24 auf die beiden
geometrischen Figuren aus 13 und 11
Elementen.
Die FS
2064 bildet mit der ZS das Verhältnis 24*(86:511) = 24*597 = 72*199. Der FW
211 stellt das Kreisflächenverhältnis 3:1 dar, diesmal in der Umkehrform. Die FW-Summe
54+89 = 143 = 11*13 verweist auf die beiden geometrischen Figuren des
Oktaeders, beide zusammen bilden die "Fischfigur" aus 14 Elementen + 3 Dreiecken.
7.
Man kann die beiden Rechnungen miteinander verbinden. Die beiden FS
sind 112+2064 = 2176 = 2*1088 = 2*(64*17).
Man erkennt an den Einzelziffern der Zahl 1088 die Zusammensetzung einer Oktaederhälfte, wie oben
dargelegt. Die beiden ZS sind 8088+12264 = 24*(337+511) = 20352
= 24*848 = 128*3*53 > FW 70.
Das summierte FS:ZS-Verhältnis beträgt 2176:20352 = 128*(17:159) = 128*176 = 211*11 = FW 33.
8.
Der Faktor 337 der Gesamtsumme 8088 bezeichnet in seinen Einzelziffern das Muster der 13 Punkte des Hexagramms
mit seinen zwei Tetraktys, der FW 346 = 2*173 für jede Tetraktys 3 "Fischfiguren"
aus 17 Elementen:
|
|
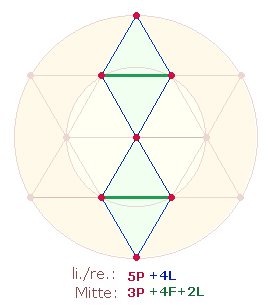
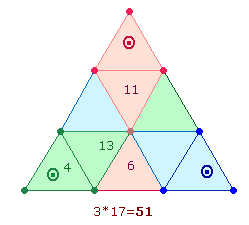
Die zweimal 9 dreistelligen Umkehrzahlen können so angeordnet
werden, daß jeweils zwei im Mittelpunkt zusammenlaufende Doppeldreiecke mit
einem zusammengehörigen Zahlenpaar und die Eckdreiecke mit den restlichen drei
Zahlen besetzt werden:
|
|
Die Anordnung der Zahlen beginnt aufsteigend mit der
Zahl 156 und der zugehörigen Entsprechung 273.
Es folgen im Uhrzeigersinn 168
und 276 mit ihren Entsprechungen 294
und 384. Wieder von 156 ausgehend werden in
aufsteigender Folge und im Uhrzeigersinn die Einzelzahlen 144, 169
und 299 in die Eckdreiecke eingetragen. In grüner Farbe sind die Umkehrungen in den Dreiecken der entgegengesetzten
Tetraktys angeordnet.
Teilt man das Hexagramm in eine obere und untere
Hälfte, entsprechen die ZS denen der oben einander zugeordneten Rauten des DR-Kreuzes,
wobei drei Zahlen nicht miteinander übereinstimmen, aber gegenseitige
Umkehrungen darstellen:
|
DK |
144 |
384 |
672 |
1200 |
|
Hex. |
441 |
483 |
276 |
1200 |
|
|
+297 |
+99 |
-396 |
|
9.
Auch bei anderer
Anordnung bleibt die Gesamtsumme der hexagonalen Zahlen gleich. Es würden sich
dabei jedoch die Summen für die einzelnen Fischfiguren ändern. Es sollen der
Kürze halber nur die Summen der beiden Tetraktys betrachtet werden.
Die Summen der 2*3 Umkehrpaare des
Hexagons die 3 einzelnen der Erweiterungsdreiecke wurde bereits oben
ermittelt: 14*363 = 5082 und 3006
= 18*167. Die FW
der beiden Summen sind 34+175
= 209 = 11*19. Die beiden Faktoren 11 und 19
sind Additionen von Durchmesser und Radialelementen des hexagonalen Kreises und
des erweiterten Tetraktyskreises. Der Doppelaspekt kann durch ein Achsenkreuz
dargestellt werden:
|
|
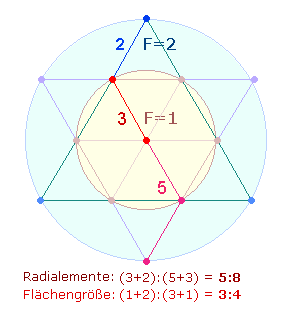
Die beiden Faktoren geben das Kreisflächenverhältnis 1:3 wieder. Die Unterscheidung zwischen hexagonalem und
Erweiterungsbereich zeigt sich auch in den FS 356
und 199. Erstere bezieht sich auf 3
hexagonale Achsen mit dem Doppelaspekt von 5 Durchmesser- und 6
Radialelementen. Die Primzahl 199 läßt sich verstehen als Mittelpunkt + 9 Tetraktyspunkte
und 9 Dreiecke. Wiederum wird darin das trinitarische
Verhältnis 1:3
sichtbar.
10. Die Umkehrsummen der 3 Zahlenpaare in
den Erweiterungsdreiecken sind:
|
144 |
169 |
299 |
612 |
|
441 |
961 |
992 |
2394 |
|
612
= 36*17;
2394 = 126*19 |
|||
|
612:2394
= 18*(34:133) |
|||
Will man die Gesamt-ZS
jeder Tetraktys ermitteln, beträgt ihre Differenz demnach 99*18 = 1782. Die beiden Summen und ihre FW sind:
5694 = 2* 3* 13* 73 >FW 91
7476 = 4* 3* 7* 89 >FW 103
13170 = 30*439 >FW 449
Man erkennt in den Faktoren die
13 Punkte des Tetraktyssterns und die 7+3
Punkte der Tetraktys. Die Zahl 91 ist die Summe der Zahlen 1-13.
Der FW 91 der Zahl 5694 läßt sich in das
Verhältnis 13:78 = 1*(1:6) setzen. Auch der FW 103
ist auf die 13 Punkte des Hexagramms beziehbar.
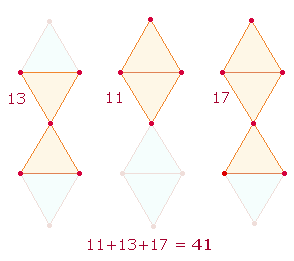
11. Da die Dreiecke beider
Tetraktys mit Zahlen besetzt sind, kann man die drei Figuren – die linke,
mittlere und rechte – entweder als "Fischfiguren" oder als
Doppelrauten sehen. Zwischen der linken und rechten Figur herrscht Symmetrie
hinsichtlich der Quadratzahlen 144 und 169,
nicht jedoch hinsichtlich der hexagonalen ZS.
Die ZS der rechten und mittleren Figur ist 5*363, die der linken 4*363.
12.
Die linke Figur
enthält die Faktoren 12, 13, die rechte 12, 13, 23, nur die
mittlere enthält außer 12,
13, 23 auch den Faktor 14.
Auf diese Weise besteht Übereinstimmung zwischen 9 verschiedenen
Zahlen und der Aufteilung der vier Faktoren auf die drei geometrischen Figuren
in absteigender Folge 3-3-2-1. Die Quersumme der Ziffern beträgt 36,
das Verhältnis der Umkehrsummen 135:261 = 9*(15:29).
13.
Wenn die Logik
der Anordnung stimmt, mag man darüber staunen, was zustande kommt, wenn man den
je drei Zahlen einer Figur die Nummern ihrer Reihenfolge zuordnet und die
Ziffern dreistellig liest. Ausgangspunkt ist das linke hexagonale Dreieck der
oberen Tetraktys, es folgen die beiden anderen gegen den Uhrzeigersinn:
|
156 |
273 |
144 |
294 |
168 |
299 |
276 |
384 |
169 |
|
2 |
5 |
1 |
7 |
3 |
8 |
6 |
9 |
4 |
Die ZS+FS
der drei ermittelten Zahlen und ihrer Umkehrung sind:
|
Zahl |
251 |
738 |
694 |
1683 |
152 |
837 |
496 |
1485 |
3168 |
|
FW |
251 |
49 |
349 |
649 |
25 |
40 |
39 |
104 |
753 |
|
1683:1485 = 9*11*(17:15); 753 = 3*251 |
|||||||||
Die beiden ZS sind jeweils durch 11
teilbar. Die FS 753
ist dreimal so groß wie der erste FW 251.
Die FW der jeweils 6 Umkehrungen der drei zusammengesetzten
Zahlen sind:
|
|
251 |
125 |
512 |
215 |
521 |
152 |
|
|
FW |
251 |
15 |
18 |
48 |
521 |
25 |
878 |
|
|
738 |
873 |
387 |
783 |
378 |
837 |
|
|
|
49 |
103 |
49 |
38 |
18 |
40 |
297 |
|
|
694 |
469 |
946 |
649 |
964 |
496 |
|
|
|
349 |
74 |
56 |
70 |
245 |
39 |
833 |
|
2008 = 8*251 |
2008 |
||||||
Die 6:12 Umkehrungen haben das FS-Verhältnis 251*(3:5). Die Primzahl 251 ist
hier zu verstehen als 2*51
= 2*(3*17): Jede Tetraktys enthält 3
"Fischfiguren" aus je 17 Elementen. 3:5
Radialelementen entspricht das Kreisflächenverhältnis 1:3:
|
|
Erstellt: Mai
2015