169 Primzahlen in 6 konzentrischen Quadraten

a) Einleitung

b) Horizontale Hälften

c) Begrenzende und umgrenzte Zahlengruppen

d) Erweiterung von 169 auf 177 Zahlen

e) Dreiheit und Einheit der göttlichen Personen

f) Erweiterung auf 198 Zahlen

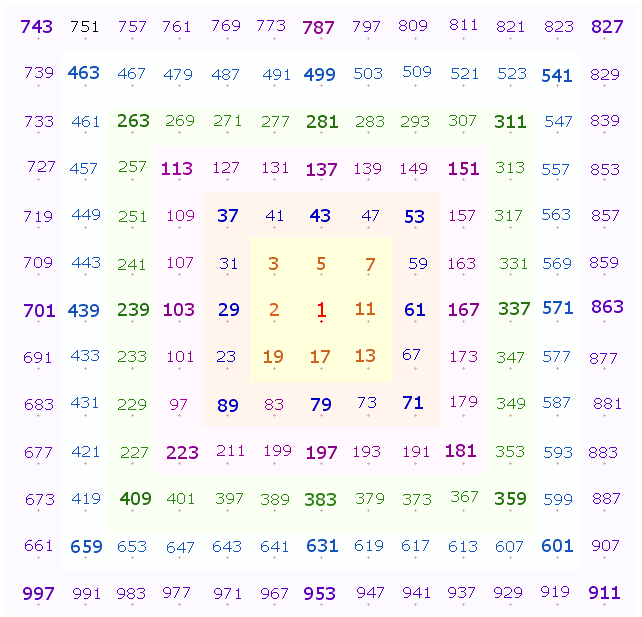
169 Primzahlen horizontal von oben nach unten angeordnet

a) Einleitung

1. Wie die ganze Schöpfung gehen auch die Zahlen aus dem Geist eines unendlich weisen Gottes hervor. Wenn man sich die Zahlen als eine unendlich lange Aneinanderreihung vorstellt, sind sie nicht sinnvoller anzuordnen als auf den Punkten in Einzelquadraten stetig wachsender Quadratrahmen. Dies gilt für alle Zahlen in fortlaufender Reihenfolge, aber auch in Anordnungen nach anderen Gesichtspunkten, so besonders nach Primzahlen und zusammengesetzten Zahlen. Der Unterschied zwischen beiden ist einfach: Primzahlen bestehen aus einem Faktor, zusammengesetzte Zahlen aus zwei und mehr Faktoren größer 1, da sich eine Zahl durch die Multiplikation mit 1 nicht verändert (Jede Vervielfältigung beginnt notwendigerweise mit 1, ebenso jede Teilung). Die Zahl 1 mag besondere Eigenschaften haben, aber sie besteht wie jede Primzahl aus einem Faktor. Wenn Zahlen eine Aneinanderreihung darstellen, dann ist ihr Ursprung die Zahl 1.

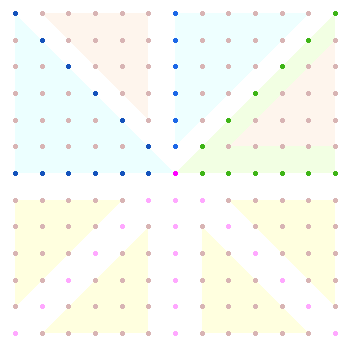
2. Mit der Zahl 1 gibt es von 1-1000 169 = 13x13 Primzahlen. Sie kann man, vom Mittelpunkt ausgehend, in 6 konzentrischen Quadratrahmen anordnen. Diese wachsen jeweils um weitere 8 Zähler, also 8+16+24+32+40+48 = 168. Daß es sich dabei um eine tatsächliche Ordnung handelt, kann man an proportionalen Verhältnissen sehen. Von der Mittelpunktzahl 1 ausgehend, endet jeder quadratischer Umlauf mit einer Quadratzahl, angefangen von 3² und nachfolgend im Abstand von 2 (5², 7² usw.).

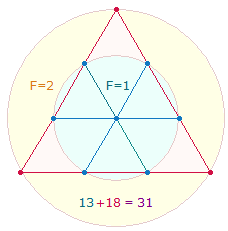
Ein sinnvolles Ordnungselement läßt sich darin erkennen, daß die Summe dieser 13x13 Primzahlen wiederum durch 13 teilbar ist: 76128 = 96*13*61 = Faktorenwert (FW) 87. Die ungerade Zahl von 169 Primzahlen ergibt eine gerade Summe wegen der geraden Primzahl 2.

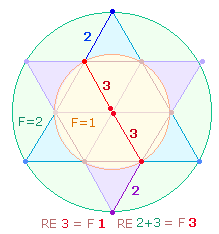
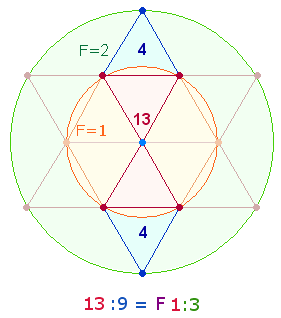
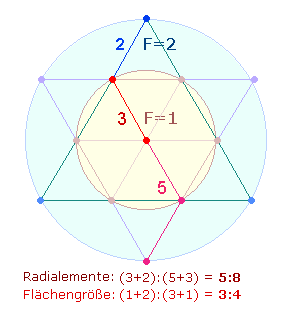
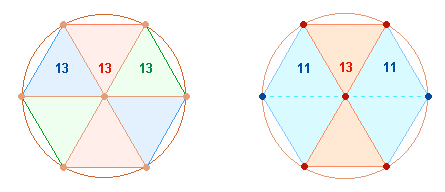
3. Wenn wir vom göttlichen Ursprung der Zahlen ausgehen, dann gibt die Zahl 13 in besonderer Weise den einen Gott in drei Personen wieder. Grundlegendes geometrisches Bezugsmodell hierfür ist der Tetraktysstern (das Hexagramm), der aus 13 Punkten sowie aus einem inneren und äußeren Kreis besteht, deren Flächenverhältnis 1:3 ist. Die Zahl 13 wird also ein besonderes Untersuchungskriterium sein.

4. Den Mittelpunkt durchlaufen 4 Achsen. Wem der Mittelpunkt zufällt, ist nicht festgelegt, vielmehr hat jede Achse Anspruch auf einen Mittelpunkt. Die folgende Arbeit möchte einige Ordnungselemente aufzeigen.

b) Horizontale Hälften

1. Bei einer ungeraden Zahl von Elementen übernimmt eine Hälfte die symmetrische Mitte, die zweite Hälfte lehnt sich an die Symmetrie der ersten Hälfte an. Die symmetrische Mitte kann eine ganze Zeile sein, hier also 13 Zahlen der 7. Zeile, oder der Symmetriemittelpunkt als einzelne Zahl 1. In der vorliegenden Anordnung der 169 Primzahlen teilt der Faktor 13 das Quadrat horizontal zweimal gemäß den beiden genannten Möglichkeiten:

743	751	757	761	769	773	787	797	809	811	821	823	827	10229
739	463	467	479	487	491	499	503	509	521	523	541	829	7051
733	461	263	269	271	277	281	283	293	307	311	547	839	5135
727	457	257	113	127	131	137	139	149	151	313	557	853	4111
719	449	251	109	37	41	43	47	53	157	317	563	857	3643
709	443	241	107	31	3	5	7	59	163	331	569	859	3527
701	439	239	103	29	2	1	11	61	167	337	571	863	3524
691	433	233	101	23	19	17	13	67	173	347	577	877	3571
683	431	229	97	89	83	79	73	71	179	349	587	881	3831
677	421	227	223	211	199	197	193	191	181	353	593	883	4549
673	419	409	401	397	389	383	379	373	367	359	599	887	6035
661	659	653	647	643	641	631	619	617	613	607	601	907	8499
997	991	983	977	971	967	953	947	941	937	929	919	911	12423
9453	6817	5209	4387	4085	4016	4013	4011	4193	4727	5897	8047	11273	76128

Bei der ersten Aufteilung ist das Summenverhältnis der oberen 6 zu den unteren 7 Zeilen 33696:42432 = 96*13*(27:34) = 96*13*61. FW (13+13)+(9+19) = 54. Wir finden in diesem Verhältnisausdruck alle Hinweise auf die Elemente des Oktaeders, der aus einem Doppelrautenkreuz zusammengefügt werden kann: Die Zahl 96 setzt sich zusammen aus 4*(11+13), den Elementen zweier geometrischer Figuren, die wechselseitig die Oberfläche des Oktaeders abdecken. Der FW von 96 ist 13, und aus 26 Außenelementen besteht der Oktaeder; fügt man das Volumen hinzu, sind es 27 Elemente. Aus 2*(9+8) = 34 Elementen bestehen zwei Oktaederhälften, aus 2*27 = 54 Elementen der Tetraktysstern mit seinen beiden konzentrischen Kreisen. Den Faktor 61 kann man als 6 Oktaederecken + Volumen deuten. 96*27 2592+271 2683

Die oberen 6 Zeilen enthalten 78 Zahlen, das bedeutet den Durchschnittswert 432 je Zahl.

2. Bei der zweiten Aufteilung gehört die horizontale Symmetrieachse mit Ausnahme der 1 des Mittelpunktes zur oberen Hälfte. Die Summe 3523 der 12 Zahlen der Horizontalachse hat die Faktoren 13*271. Das entsprechende Zahlenverhältnis ist nun 37219:38909 mit den Faktoren 7*13*409 = FW 429 = 3*11*13 und 13*41*73 = FW 127, zusammen 556 = 4*139 > 143 = 11*13. Der Abstand zwischen beiden Summen beträgt 1690, das Zehnfache der 169 Zahlen.

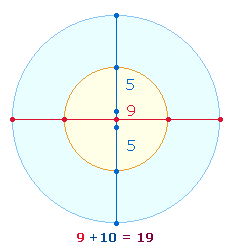
Die Einzelziffern der Faktorensumme (FS) 556 zeigen die Symmetriemitte der Zahlen 1-9 und 1-10. In zwei konzentrischen Kreisen besteht der Durchmesser aus 9 Elementen und die zwei Radialhälften aus 2*5 Elementen:

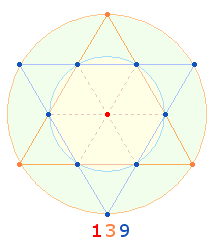
Die Zahlen 9 und 10 sind unter diesem Gesichtspunkte konstitutiv für das Dezimalsystem. Da der Faktor 139 noch mehrmals auftritt, soll hier auf diese Zahl eingegangen werden. Die Einzelziffern stimmen mit dedr Aufteilung der 13 Punkte des Hexagramms überein:

In der Aufteilung 13+9 weist die Zahl 139 auf zwei Achsenkreuze hin, die 6+4 = 10 Maßeinheiten enthalten:

Der Oktaeder setzt sich aus beiden Achsenkreuzen zusammen: Zwei Doppelrauten (DR) gehen auf die drei Achsen des Hexagons zurück, das Achsenkreuz aus zwei Doppelrauten vertritt das Prinzip der Zweiachsigkeit.

Die Faktoren 11 und 13 beziehen sich wiederum auf die beiden geometrischen Figuren, aus denen der Oktaeder zusammengesetzt ist.

3. Die obere und untere Hälfte besteht nun in doppelter Zählung aus 78+90 = 168 und 91+79 = 170 Zahlen. Die FW der vier Zahlen sind wiederum durch 13 teilbar: 18+13+20+79 = 130. Das FS:ZS-Verhältnis beträgt demnach 26*(5:13).

4. Ein weiteres durch 13 teilbares Zahlenverhältnis findet sich in vertikaler Anordnung: 7 konzentrische innere Reihen ergeben zu den zweimal 3 äußeren Reihen das Verhältnis 29432:46696 = 6*13*(283:449) = FW 770.

c) Begrenzende und umgrenzte Zahlengruppen

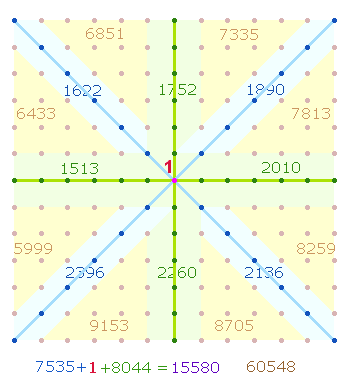
1. Eine wichtige Rolle spielen die vier Achsen, die aus 8*6+1 = 49 Zahlen bestehen und in 8 Achsenarme (A) und den Mittelpunkt einzuteilen sind:

1622	1752	1890	5264
1513	1	2010	3524
2396	2260	2136	6792
5531	4013	6036	15580
15580 = 20*19*41 >FW 69

5 Achsenarme und der Mittelpunkt sind jeweils als eine Hälfte anzusehen. Die Summen der oberen Hälfte und der rechten Hälfte sind jeweils durch 13 teilbar:

			sm	Faktoren	FW	sm	FW
ob.	5264	3524	8788	4*13³	43
re.	4013	6036	10049	13*773	786
sm	63*13*23		18837
FW			49		829	878	441
441 = 21*21

Der untere linke Achsenarm mit der Summe 2396 bleibt als einziger unberücksichtigt.

Die Zahlen keines Achsenarmes – mit und ohne Mittelpunkt – sind durch 13 teilbar.

2. Ein Achsenarm besteht – ohne Mittelpunkt – aus 6 Zahlen. Die 8 Achsenarme begrenzen 8 gleichseitig-rechtwinklige Felder aus 15 Zahlen, die sich von 1-5 aufbauen:

Die Summen dieser 8 Dreiecksfelder (F) und 120 Zahlen sind:

	links		sm	rechts		sm	GS
oben	6433	6851	13284	7335	7813	15148	28432
unten	5999	9153	15152	8705	8259	16964	32116
	12432	16004	28436	16040	16072	32112	60584
60584 = 8*7573; 6851 = 17*13*31; 7813 = 13*601

Die vier Gesamtsummen sind jeweils durch 4 teilbar, die Differenz von je zwei horizontalen und vertikalen Summen ist jeweils 4.

Zwei Dreiecksfelder sind durch 13 teilbar. Ihre Summe hat mehrere Faktoren mit den Faktoren der Gesamtsumme gemeinsam: 14664 = 24*13*47. Bemerkenswert an dem Ergebnis ist, daß die Differenz zu 76128 aus denselben Ziffern besteht: 14664:61464 = 312*(47:197) = 312*244.

3. Da die 8 Achsenarme die Dreiecksfelder (F) umgrenzen, möchte man annehmen, daß die Verbindung beider zu Summen führen, die durch 13 teilbar sind. Dies ist in erstaunlicher Variabilität der Fall. Zuerst soll die obere Hälfte betrachtet werden, in die die horizontale Mittelachse (ohne Mittelpunktzahl 1) einbezogen ist, sodaß 9 Zahlensummen zu behandeln sind:

In der oberen Hälfte sind 4 durch 13 teilbare Zahleneinheiten zu finden:

– Die linke besteht aus zwei Achsenarmen und einem Feld. Keine der drei Komponenten ist durch 13 teilbar, aber alle drei zusammen: 9568 = 32*13*23.

– Das Feld daneben ist allein durch 13 teilbar: 6851 = 13*17*31.

– Der vertikale Achsenarm ist zusammen mit dem rechten Zahlenfeld daneben durch 13 teilbar: 9087 = 3*13*233.

– Rechts befindet sich die symmetrische Entsprechung zu den linken drei Zahlengruppen. Hier sind beide Achsenarme zusammen (3900 = 300*13) und das Zahlenfeld (7813 = 601*13) jeweils durch 13 teilbar.

Die obere Hälfte ist demnach teilbar in 2 linke und 3 rechte Zahleneinheiten, das sind 42+48 = 90 Zahlen.

Die Summen der 4 Einheiten von links nach rechts sind:

	A1	A2	sm	F	GS
1	1513	1622	3135	6433	9568	13*32*23	46
2				6851	6851	13*17*31	61
3	1752		1752	7335	9087	3*13*233	248	8*31
4	2010	1890	3900	7813	11713	13*17*53	83
			8787	28432	37219	7*13*409	438	6*73

d) Erweiterung von 169 auf 177 Zahlen

1. In der unteren Quadrathälfte sind drei gleichartige und zusammenhängende Zahleneinheiten zu erkennen:

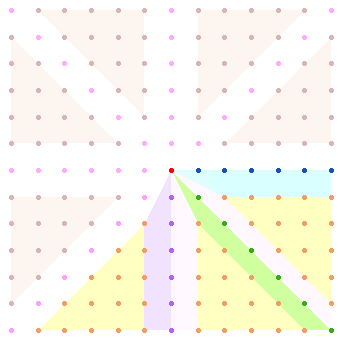
Die drei Zahleneinheiten vermitteln den Eindruck einer Drehung im Uhrzeigersinn, die der Anordnung der Zahlen selbst entspricht. Das rechte Zahlendreieck lehnt sich an die darüber befindliche Horizontalachse an, das Zahlenfeld daneben an die Diagonalachse und das linke an den unteren vertikalen Achsenarm.

Die Summen der drei Achsenarme und Zahlenfelder sind ein Wunder der Harmonie: Die zwei Differenzen von links nach rechts betragen einmal 2 mehr und einmal 2 weniger, sodaß sich der Unterschied aufhebt:

	links-Mitte	sm	Mitte-rechts	sm
Achse	2260-2136	124	2136-2010	126
Feld	9153-8705	448	8705-8259	446
sm		572		572
572 = 4*11*13

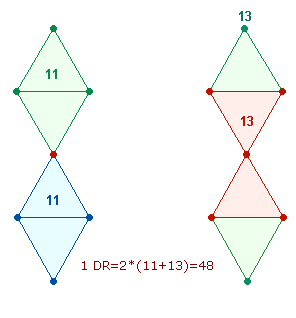
Die Faktoren 4*11*13 geben in multiplikativer Form wieder, was in der Abwandlung 4*(11+13) = 96 einem Teiler der Gesamtsumme 76128 entspricht. Es handelt sich um die Elemente der Raute und des sanduhrförmigen Doppeldreiecks, die jeweils vierfach die Oberfläche des Oktaeders zusammensetzen:

Die mittlere Zahleneinheit bildet also die Symmetriemitte der beiden nebenstehenden, d.h., letztere betragen das Doppelte.

Die Summe der mittleren Zahleneinheit ist 8705+2136=10841 = 37*293. Die Zahl 37 verweist auf 3+7 Punkte und 37 Elemente der Tetraktys sowie 3*7 Elemente der Doppelraute (DR), die Zahl 293 auf 3 DR-Kreuze, deren Rahmen aus jeweils 29 Elementen besteht:

Die dreifache Summe ist das Zahlenpalindrom 32523 = 3*37*293, das auf die Radialelemente des Tetraktyssterns hinweist:

5 Elemente betreffen den ganzen äußeren Kreis, hier zweimal aufgeteilt in 3+2.

2. Die Einheit der drei Zahlenfelder besteht darin, daß sie zusammen durch 13 teilbar sind: 9153+8705+8259 = 26117 = 7*7*13*41.

Die Zahl 1 des Mittelpunktes wurde bisher noch nicht hinzugenommen. Erhöht man mit ihr die mittlere Summe der Diagonalachse von 2136 auf 2137 und addiert die Feldsumme 8705, ergibt 10842 Teilbarkeit durch 13: 2*3*13*139. Da nun die Differenz 572 zur tieferen und höheren Zahleneinheit ebenfalls durch 13 teilbar ist, ergibt sich durch erneute Hinzunahme des Mittelpunktes 1 für die anderen beiden Zahleneinheiten wiederum Teilbarkeit durch 13. Wenn aber die Summe der drei Zahlenfelder zusammen durch 13 teilbar ist und ebenso die drei Zahleneinheiten, dann muß auch die Summe der drei Achsen durch 13 teilbar sein: 6409 = 13*493 = 13*17*29. Die Gesamtsumme beträgt nun 26117+6409 = 32526 = 18*13*139, also das dreifache der mittleren Summe 10842.

Die Primzahl 2137 vereinigt 21 Elemente der DR und 37 Elemente der Tetraktys.

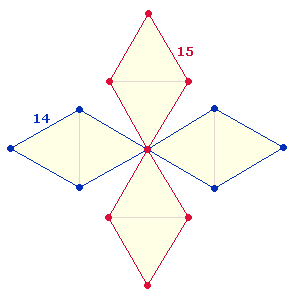
Über die Bedeutung der Primzahl 139 wurde bereits oben gesprochen. Die Einzelziffern des Produkts 6*13 können auf die 10 Punkte der Tetraktys, der Zahl 139 auf die 13 Punkte des Hexagramms bezogen werden. Nun ist folgendes zu bedenken: Durch die Hinzufügung der Mittelpunktszahl besteht eine Zahleneinheit aus 15+7 = 22 Zahlen. Eine DR besteht zwar aus 21 Punkten, zählt man den Mittelpunkt jedoch zweimal, sind es 22. Der hexagonale Anteil der DR ist das Doppeldreieck aus 13 Elementen, durch die Erweiterung kommen 4+4 hinzu. Hexagonaler Kreis und Erweiterungskreis haben das Flächenverhältnis 1:2 oder 1:3, je nachdem ob man nur den Erweiterungsring rechnet oder den ganzen äußeren Kreis. Der zweite Kreisbogen erfordert die nochmalige Verwendung des Mittelpunktes. Daher läßt sich zu den 8 Erweiterungselementen noch der zweite Mittelpunkt hinzudenken:

Den 15+7 Zahlen einer Zahleneinheit entspricht auch der FW 157 der mittleren Summe 10842. Die Einzelziffern dieser schwierigen Zahl lassen sich auf ein unnumeriertes und zwei numerierte Modelle der Tetraktys und des Oktaeders beziehen. Numeriert man nur die Punkte der Tetraktys, ist der Mittelpunkt 5, numeriert man das ganze Hexagramm, ist es die Zahl 7. Dasselbe gilt für das Volumen des Oktaeders, je nachdem ob man die DR-Elemente von 1-4 oder 1-6 numeriert.

Die Zahlen 11 und 13 sind in der Primzahl 113 kontrahiert. Die Summe der Zahlen des vertikalen Achsenarmes und des Zahlenfeldes sind jeweils durch 113 teilbar: 2260:9153 = 113*(20:81) = 113*101 = 11413 = FW 224.

3. Es bleiben in der unteren linken Ecke die Summen 2396 und 5999 des diagonalen Achsenarmes und des Zahlenfeldes übrig. Sie sind weder allein noch zusammen durch 13 teilbar und lassen sich auch nicht in eine größere Einheit einbinden, die Teilbarkeit durch 13 aufweist. Ihre Bedeutung ist gleich zu untersuchen.

Zur Zahl der 169 Primzahlen sind nun 8 hinzugekommen, 2 Mittelpunkte und 6 Achsenzahlen. Das hängt einerseits damit zusammen, daß vier Achsen Anrecht auf einen Mittelpunkt haben, aber nur einer sichtbar ist, andererseits beide Quadrathälften Anteil an einer Mittelachse haben. Die beiden Felder, die Anteil am selben rechten horizontalen Achsenarm haben, verbinden also insgesamt 4 Felder zu einer zusammengehörigen Einheit. Ein Hinweis sind die beiden 5-stelligen Summen, die in zwei- und dreistelliger Aufteilung durch 13 teilbar sind: die Gesamtsumme 11713 der einzelnen Zahleneinheit in der oberen Hälfte (27 Zahlen) und die Summe 26117 der drei Felder allein (45 Zahlen). Es wird auf diese Weise eine diagonale Teilung von unten links nach oben rechts erkennbar:

Es stehen sich zweimal je zwei Felder auf beiden Seiten der Diagonale gegenüber, vier horizontal, vier vertikal. Die Diagonale selbst ist geteilt in zwei Zugehörigkeiten von links und rechts.

Der untere linke Achsenarm der Diagonale ist thematisch mit dem Zahlenfeld links von ihm verbunden. Es zeigt sich eine innere Verbindung zwischen den nunmehr 169+8 = 177 = 3*59 Zahlen und den beiden Summen 5999 und 2396:

	F	A	sm	FW
ZS	5999	2396	8395	101
FW	864	603	1467	169
sm	1467 = 5*163			270
5999 = 7*857; 2396 = 4*599
6895 = 5*23*73

Die FS 1467 vereinigt wieder 14+(6+7) Punkte des Hexagramms in der Bedeutung von 4+3 Flächeneinheiten, 163 zeigt in den Einzelziffer die 10 Tetraktyspunkte.

Die Faktoren 857 und 599 geben beide 4+3 Flächeneinheiten wieder, der erste als 8:5 Radialelemente und 7 Flächeneinheiten, der zweite als (5+9)+9 Durchmesserelemente der Doppelraute:

Die Doppelraute besteht aus 15 Rahmenelementen, aufgeteilt in 1+7+7. Aus 177 Elementen besteht jedoch auch ein numeriertes Achsenkreuz AK9:

Während 7 Kreisflächeneinheiten durch 13 Radialelemente dargestellt werden, sind es (9+5)+9 = 23 Durchmesserelemente. Das könnte der Grund sein, daß die beiden unteren Summen schwerpunktmäßig die Durchmesserelemente vertreten. Aber läßt man von 1467 die Faktoren 7 und 4 weg, erhält man wiederum Teilbarkeit durch 13: 1456 = 8*7*13 mit Hinweis auf die 15 Rahmenelemente der DR. Da nicht nur die beiden Zickzacklinien der DR aus 9 Elementen bestehen, sondern auch der Mittelteil mit 4 Dreiecken, 2 Querlinien und 3 Schnittpunkten, erscheint dreimal die Ziffer 9 in 5999 sinnvoll.

e) Dreiheit und Einheit der göttlichen Personen

1. Die drei göttlichen Personen verbergen sich also wie ein Vexierbild in drei unteren Feldern mit je einem Achsenarm. Es wurde deutlich, daß die mittlere Figur den Mittelwert der drei äußeren hat. Man wird sie daher der 3. göttlichen Person, der Liebe des Vaters und des Sohnes, zuweisen. Im Hexagon sind die drei göttlichen Personen auf zwei Weisen darstellbar:

In der linken Figur sind drei gleiche Doppeldreiecke erkennbar, in der rechten stehen links und rechts zwei Rautenfiguren aufrecht, sie werden verbunden durch die mittlere Figur. Im vorliegenden Quadrat wird man die erste hexagonale Figurenkonstellation der unteren Hälfte zuordnen, die zweite der oberen.

2. Das Quadrat mit seinen zweimal 4 Feldern bietet die Möglichkeit, auch die Einheit in der Dreiheit sichtbar werden zu lassen. Im Quadrat ist es das 4. und das 8. Zahlenfeld: Die vier Figuren stehen einander spiegelbildlich gegenüber:

Die drei göttlichen Personen sind farblich gekennzeichnet: blau für die erste, rosa für die dritte, grün für die zweite Person und hellbraun für die Einheit in der Dreiheit.

Die oberen und unteren drei Zahleneinheiten sind jeweils durch 18*13 teilbar: 25506:32526 = 18*13*(109:139) = 234*(109:139) = 234*248 = 144*13*31 = 58032. In den Umkehrfaktoren erweist sich die Vermittlung der dritten Person, denn das einzelne obere Zahlenfeld hat die Summe 6851 = 17*13*31.

Die Einzelziffern der Faktoren 109 und 139 lassen sich auf die 10 Tetraktyspunkte und 13 Hexagrammpunkte beziehen. Die Kombination von 13 und 18 weist auf die 13 Achsenelemente des Hexagons und die 18 Rahmenelemente der Tetraktys hin:

3. Besondere Aufmerksamkeit verdient der gemeinsame rechte Achsenarm für die zwei rechten Zahleneinheiten: die obere der Einheit in der Dreiheit und die untere der ersten Person. Für die obere ist die Summe 2010, für die untere 2011, zusammen die Primzahl 4021. Die Einzelziffern legen die beiden trinitarischen Kreisflächenverhältnisse 3:1 und 2:1 nahe. Sie zeigen sich bei einer ZW/FW-Verrechnung der Summen beider Zahleneinheiten:

			sm	FW	sm
ZS	11713	10270	21983	121
FW	83	99	182	22
sm			22165	143
FW			60	24	84
182 = 13*14; 11713 = 10*13*53; 10270 = 13*17*53;
21983 = 13*19*89; 60:24 = 12*(5:2)
22165 = 5*11*13*31 = FW 24:36 = 12*(2:3)

Die Faktoren 13 und 14 der Summe 182 sind auf die Punkte des Hexagramms und seiner zwei konzentrischen Kreise zu beziehen, wie oben schon dargelegt wurde: 13 Punkte bedeuten 3 Flächeneinheiten, 7+7 Punkte 1+3 Flächeneinheiten. 182 ist die Zahlensumme der Aussage SATOR OPERA TENET – Der Schöpfer erhält seine Werke.

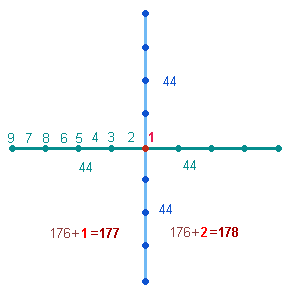
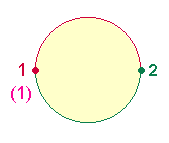
Die Palindromzahl 121 ist ein Kreissymbol, das die Ewigkeit Gottes besonders veranschaulicht. Sie entsteht, wenn man den Kreisbogen halbiert und mit 1 und 2 numeriert: Die zweite Kreisbogenhälfte kehrt zur 1 zurück:

Die Doppelraute besteht aus zwei Rauten von je 11 Elementen. Durch einen Mittelpunkt wird die Zahl der Elemente auf 21 herabgesetzt. Auch sie ist ein Kreissymbol, da sie durch Verbindung der Endpunkte und im Achsenkreuz mit einer weiteren Doppelraute zum dreidimensionalen Körper des Oktaeders zusammensetzbar ist.

Durch Vereinigung der Endpunkte wird die Zahl der DR-Elemente noch einmal um 1 auf 20 reduziert. Damit wäre der vordere Teil der addierten Achsensumme 4021 erklärt. Der hintere Teil setzt sich aus 10+11 zusammen. Dies könnte durch folgende zwei Punktenumerierungen geschehen:

Die Punkte sind reihum bis zum Ausgangspunkt numeriert. Durch die Vereinigung der Außenpunkte wird eine 10. Position geschaffen. Diese wird unter zwei Gesichtspunkten genützt: Die Zahlen 9 und 10 als Durchmesser- und Radialelemente des Doppelkreises sind konstitutiv für das Dezimalsystem. Nun gibt es nur 9 Grundzahlen, die von 0 ausgehen und in einer Kreisform dorthin zurückkehren. Wenn man mit 1 beginnt, dann steht am Ende die Null. Andererseits ist 10 eine reale Zahl, die die erste Zehnereinheit abschließt und das Weiterzählen möglich macht. In beiden Doppelrauten geht die Numerierung also bis 10. Aber die Zahl 10 besteht aus 2 Stellen. Auf diese Weise kommt die Zahl 10+11 = 21 zustande, und in der Addition 40+21 = 61. 61 ist die ZS des Wortes TENET im SATOR-Quadrat. Aus den Buchstaben des SATOR-Quadrats läßt sich PATER NOSTER bilden, seine ZS ist 143.

Der gemeinsame Achsenarm ist sinnvoll, da die trinitarischen Einheit ihren Ausgang von der 1. Person nimmt.

f) Erweiterung auf 198 Zahlen

1. Die Erweiterung von 169 zu 177 Zahlen befriedigt aus mehreren Gründen nicht:

a) Die Gesamtsumme ist nicht durch 13 teilbar:

b) Die vier Unterquadrate umfassen im Uhrzeigersinn 42, 48, 66 und 21 Zahlen. Dies erscheint als Ungleichgewicht für das vierte Quadrat.

c) Der rechte horizontale Achsenarm, der zweimal in Anspruch genommen wurde, verlangt nach einer symmetrischen Entsprechung. Ohne Mittelpunkt beträgt die Summe der beiden horizontalen Achsenarme 3523 = 13*271, ist also durch 13 teilbar.

d) Der Umlauf einer quadratischen Anordnung von Zahlen kehrt wie beim Kreis zum Anfang zurück, um zumindest durch Wiederholung der ersten Zahl den Umlauf zu schließen.

2. Tatsächlich wird die Gesamtsumme wieder durch 13 teilbar, wenn man die Zahlen des linken horizontalen Achsenarmes und des darüber befindlichen Zahlenfeldes hinzunimmt: Die Summe des vierten Quadrates beträgt dann 8395+(1513+6433) = 16341 = 3*13*419, die Gesamtsumme 76128+9958 = 86086 = 86*1001 = 2*43*7*11*13 = FW 76. In der Zahl 1001 ist eine Umkehrung und Rückkehr zum Anfang zu erkennen. Als geometrisches Modell ist an einen Kreisdurchmesser mit 0 im Mittelpunkt und 1 als Kreislinienpunkte zu denken. Von links nach rechts wird das linke Radialmaß durch 1-0 und das rechte durch 0-1 begrenzt:

In Übereinstimmung mit den Faktoren 7*13 stehen die vier Zahleneinheiten der oberen Quadrathälfte sowie die drei verbundenen unteren drei Zahleneinheiten durch 37219 = 7*13*409 und 26117 = 7* 7*13* 41. 7*13 = 91 ist die Summe der Zahlen 1-13 und somit auf die 13 Punkte des Tetraktyssterns beziehbar. Die Faktoren 13 und 11 geben die Elemente des Doppeldreiecks und der Raute in der Doppelraute wieder. Die Raute entsteht durch die Erweiterung des Hexagons zum Tetraktysstern. Die Längsdiagonale √3 der Raute ist der Radius des Hexagrammkreises und daher von besonderer Bedeutung. Die Doppelraute selbst bietet ein Modell der Umkehrung 3+1 und 1+3 Punkten:

3. Die ursprünglich 49 Zahlen der 4 Achsen werden durch 2*6+2 = 14 Zahlen der Mittelachse auf 63 erhöht. Die beiden Summen geben 49 Elemente des Tetraktyssterns und 63 = 3*21 Elemente von drei Doppelrauten wieder, die 2*6 Elemente miteinander teilen; von drei Mittelpunkten werden 2 eingespart:

Erstellt: August 2016

Ergänzt:2024

Inhalt II