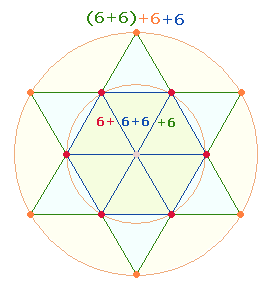
Primzahlabstand 6
a) 2*12 Primzahlen von 1-100
b) 2 Primzahlreihen von 1-1000
d) 2 Primzahlreihen in 4 Quadratrahmen
e) Zusammenschau der Zahlen 1-81 und der 2 Primzahlreihen
a) Zwei
Primzahlreihen von 1-100
1. Die folgenden Ausführungen setzen die Ergebnisse über den Primzahlabstand 6 und zwei parallele Primzahlreihen fort. Die eine Primzahlreihe beginnt mit 1, die zweite mit 5. Für die Zahlen 1-100 gibt es je 12 Primzahlen mit der gleichen Zahlensumme (ZS) 528 = 11*48 = 12*44:
|
|
7 |
13 |
19 |
31 |
37 |
43 |
61 |
67 |
73 |
79 |
97 |
528 |
|
|
|
5 |
11 |
17 |
23 |
29 |
41 |
47 |
53 |
59 |
71 |
83 |
89 |
528 |
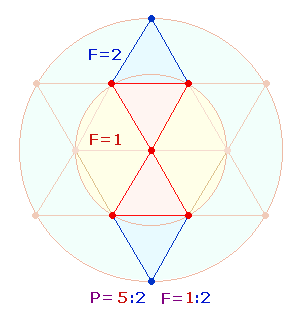
2. Die besondere Bedeutung der Zahl 528 kann an den Einzelziffern und an ihrem Faktorenwert (FW) abgelesen werden. Sie bezieht sich auf die Doppelraute (DR), die aus zwei Rauten und jeweils 11 Elementen besteht. Diese zweimal 11 Elemente der DR werden durch die Faktoren der Zahl 528 = 48*11 = FW 11+11 wiedergegeben.
Der Rahmen der Doppelraute besteht aus 5 hexagonalen und 2 Erweiterungspunkte sowie aus 8 Linien:
|
|
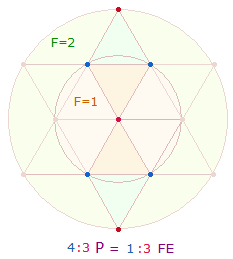
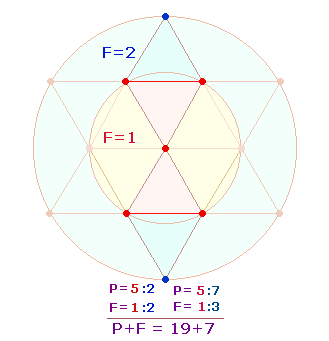
5+2 Punkte und 4+4 Linien geben in zweistelliger Zusammensetzung 52 = 4*13 und 44 = 4*11 die beiden geometrischen Figuren des Oktaeders wieder. Ihr Additionsergebnis ist 96 = 4*24. 5:2 Punkte geben das Kreisflächenverhältnis 1:2 wieder.
Die Bedeutung der beiden Primzahlreihen wird nun klar: Durch Vereinigung zweier DR in einem DR-Kreuz wird die Voraussetzung für die Bildung eines Oktaeders geschaffen.
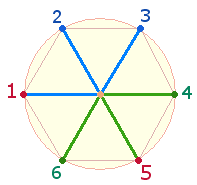
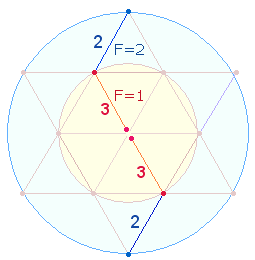
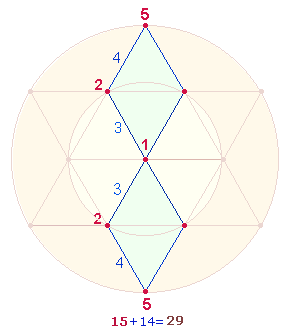
Eine einzelne Doppelraute besteht aus dreimal 9 Durchmesserelementen, die durch 3 Schnittpunkte auf 21 Elemente reduziert werden. Es ist daher nicht ausgeschlossen, daß ein 6-er Umlauf, den Holger Ullmann vertritt, Relevanz besitzt: Er könnte etwa folgendermaßen aussehen:
|
|
Die ersten drei und die zweiten drei Achsenarme gehören zusammen. Eine sinnvolle Fortführung dieses Umlaufs von 6 Zahlen könnte dann sinnvoll erscheinen, wenn von beiden Reihen aus je 3 Umlaufzahlen die Zahlensummen und Faktorensummen (FS) ermittelt werden. Für den ersten Umlauf ergibt sich 6+6 = 12 und 15+14 = 29. Die beiden Summen treffen auf die 41 Elemente eines DR-Kreuzes zu, das aus 29 Rahmenelementen und 2*6 Binnenelementen besteht.
b)
Zwei Primzahlreihen von 1-1000
1. Die beiden Primzahlreihen werden in der folgenden Tabelle von 1-1000 ausgeführt:
|
1-9 |
1 |
7 |
13 |
19 |
31 |
37 |
43 |
61 |
67 |
|
|
|
|
|
|
|
279 |
|
|
5 |
11 |
17 |
23 |
29 |
41 |
47 |
53 |
59 |
|
|
|
|
|
|
|
285 |
|
10-25 |
73 |
79 |
97 |
103 |
109 |
127 |
139 |
151 |
157 |
163 |
181 |
193 |
199 |
211 |
223 |
229 |
2434 |
|
|
71 |
83 |
89 |
101 |
107 |
113 |
131 |
137 |
149 |
167 |
173 |
179 |
191 |
197 |
227 |
233 |
2348 |
|
26-41 |
241 |
271 |
277 |
283 |
307 |
313 |
331 |
337 |
349 |
367 |
373 |
379 |
397 |
409 |
421 |
433 |
5488 |
|
|
239 |
251 |
257 |
263 |
269 |
281 |
293 |
311 |
317 |
347 |
353 |
359 |
383 |
389 |
401 |
419 |
5132 |
|
42-49 |
439 |
457 |
463 |
487 |
499 |
523 |
541 |
547 |
|
|
|
|
|
|
|
|
3956 |
|
|
431 |
443 |
449 |
461 |
467 |
479 |
491 |
503 |
|
|
|
|
|
|
|
|
3724 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18300 |
|
50-65 |
571 |
577 |
601 |
607 |
613 |
619 |
631 |
643 |
661 |
673 |
691 |
709 |
727 |
733 |
739 |
751 |
10546 |
|
|
509 |
521 |
557 |
563 |
569 |
587 |
593 |
599 |
617 |
641 |
647 |
653 |
659 |
677 |
683 |
701 |
9776 |
|
66-81 |
757 |
769 |
787 |
811 |
823 |
829 |
853 |
859 |
877 |
883 |
907 |
919 |
937 |
967 |
991 |
997 |
13966 |
|
|
719 |
743 |
761 |
773 |
797 |
809 |
821 |
827 |
839 |
857 |
863 |
881 |
887 |
911 |
929 |
941 |
13358 |
|
279+2434+5488+3956+10546+13966
= 36669; 285+2348+5132+3724+9776+13358
= 34623 |
|||||||||||||||||
Die Zahlen der ersten Reihe sind gegenüber denen in der zweiten in der Unterzahl und ihnen daher voraus. Am Ende bleiben von der zweiten Reihe 5 Zahlen übrig: 947, 953, 971, 977, 983, zusammen 4831. Die 81 Zahlenpaare haben die Summe 36669+34623 = 71292 = 12*13*457 = FW 477. Die Differenz der zweiten zur ersten beträgt 2046 = 6*11*31 = FW 47. Die Gesamtsumme der 86 Zahlen der zweiten Reihe beträgt 34623+4831 = 39454, die Differenz zur ersten 2785 = 5*557 = FW 562.
2. Wenn man zu den 5 Zahlen der zweiten Reihe noch die bisher unberücksichtigten Primzahlen 2 und 3 hinzufügt, enthält das Ergebnis wiederum die trinitarischen Umkehrzahlen 31 und 13: 4836 = 12*403 = 12*13*31 = FW 51. Das Verhältnis von 162+7 Zahlen ist 12*13*(457+31) = 156*488 = 4*24*13*61. Je 13 Zahlen haben den Durchschnittswert 5856. In den Einzelziffern 5+8 = 13 und 5+6 = 11 sind die Elemente der beiden geometrischen Figuren zu erkennen, aus denen der Oktaeder zusammengesetzt ist.
Die FW 477+51 der beiden Summen ergeben wiederum 528, die Summen der ersten zweimal 12 Primzahlen.
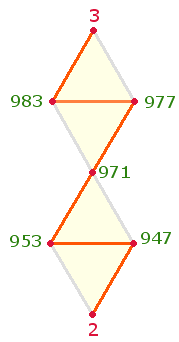
3. Es liegt nahe, die 2+5 Primzahlen auf den Punkten der DR anzuordnen:
|
|
Die Summe der unteren drei Zahlen und der Mittelpunktszahl beträgt 2873 = 13*221 =13*13*17, die Summe der oberen drei Zahlen 1963 = 13*151, zusammen 13*(221+151) = 13*372 = 12*13*31.
In dem S-förmigen Zickzackverlauf werden die 7 Punkte durch 6 Linien verbunden. Der Punkteverlauf 3+1+3 spiegelt die beiden trinitarischen Faktoren 13 und 31 wider.
4. Die beiden Zickzacklinien der DR bestehen aus 8 symmetrischen Elementen und dem Mittelpunkt. Die Einzelziffern der zweimal 81 Primzahlen lassen sich so auf zwei Durchmesserlinien der DR beziehen. Bildet man das quadratische Produkt 9*9, kann ein Achsenkreuz aus zwei DR gemeint sein, aus dem sich ein Oktaeder zusammensetzen läßt. Der FW von zweimal 81 ist 12+12 = 24. Auf diese Weise haben die ersten 24 Primzahlen gewissermaßen eine Leitfunktion.
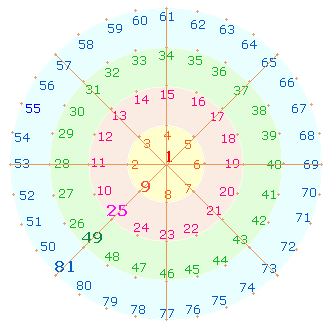
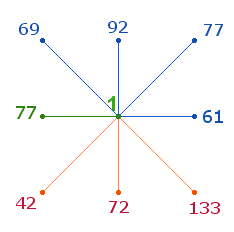
1. Numeriert man vom Mittelpunkt aus die Punkte konzentrischer Quadrate, schließt jedes mit einer Quadratzahl ab. Auf diese Weise werden 1+80 Primzahlen auf 4 konzentrischen Quadraten untergebracht, die auch in Kreisform dargestellt werden können:
|
|
Von besonderer Bedeutung sind die diagonalen Achsen und die Mittelachsen, denn sie sind die Konstanten konzentrischer Erweiterungen. Auf jedem der 8 Achsenarme befinden sich 4 Zahlen. Hinzu kommt die Mittelpunktzahl 1. In der vorliegenden Quadratausdehnung zeigt sich die Bedeutung darin, daß nicht nur die Faktorensumme (FS) aller 81 Zahlen durch 13 teilbar ist, sondern auch die 33 Zahlen der vier Achsen. Die Gesamt-FS 1612 = 4*13*31 = 26*62 enthält erneut die trinitarischen Umkehrzahlen. Die Einzelziffern von 26 und 62 sind auf je einen Mittelpunkt der DR zu beziehen, 26*62 auf ein DR-Kreuz.
Die FS der 33 Achsenzahlen beträgt 624 = 48*13 und ihr Verhältnis zu der FS 988 der 48 übrigen Zahlen 4*13*(12:19). Die Summen der 8 Achsenarme sind folgende:
|
|
Auffällig sind Teilbarkeiten durch 7, 11, 19 und 23: (77+77+42+133)+(69+1+61+72) = 7*(47+29) = 7*76 = 532; (77+77)+(92+1+72) = 11*(14+15) = 11*29; (69+92)+(61+77+1+42+72) = 23*(7+11) = 23*18 = 414.
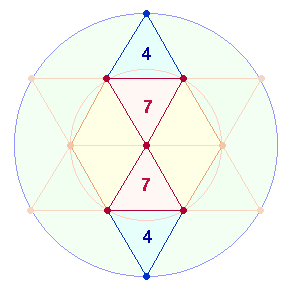
2. Keine der 9 Summen ist durch 13 teilbar, aber zweimal durch 77+1 = 78 = 6*13. Die Einzelziffern weisen zweimal auf die 15 Rahmenelemente der DR hin:
Die Faktoren 7*11 und die Einzelziffern 7+7 bedeuten zweimal das Kreisflächenverhältnis 1:3. Aus 7 Elementen besteht das Dreieck, das bei der hexagonalen Erweiterung durch 4 Elemente zur Raute wird. Das Flächenverhältnis 1:3 des inneren zum äußeren Kreis wird durch 7 Elemente des Kreises und (7+4) Elemente der Raute, die sich innerhalb beider Kreise befindet, wiedergegeben:
|
|
Aus 7+7 Punkten besteht das Hexagramm, wenn man zur Erzeugung eines äußeren Kreises den Mittelpunkt erneut verwendet.
Die Zahl 78 verbindet die Tetraktys mit der DR auf folgende Weise:
·
Aus 7+8
Elementen besteht der DR-Rahmen.
·
Das Produkt 3*26
weist auf drei Oktaeder hin, von
denen jeder aus 26 Elementen besteht, indem
jede der drei DR des Hexagramms sich mit
jeder zu drei DR-Kreuze verbindet, aus denen ein Oktaeder gebildet
werden kann. Die dreistellige Zahl 326 besteht
zweimal aus der Primzahl 163, deren
Einzelziffern den Aufbau der Tetraktyspunkte darstellen: Mittelpunkt, 6
Kreislinienpunkte, 3 Eckpunkte.
·
Das
Produkt 6*13 weist ebenso auf die 10 Punkte der Tetraktys hin.
Die oberen 6 Zahlen und die unteren 3 sind durch 13 teilbar und haben das Verhältnis 377:247 = 13*(29:19). Fügt man den linken Achsenarm und Mittelpunkt mit den Zahlen 77+1 zu den unteren drei Zahlen hinzu, ist das Verhältnis von 4:5 Zahlen 299:325 = 13*(23:25).
3. Die Zahl 81 hat besondere Beziehungen zum Tetraktysstern:
· Wie
der Tetraktysstern sich in zwei konzentrischen Kreisen befindet, so bestehen
zwei konzentrische Quadrate aus 81
Elementen: aus 25 Punkten, 40 Linien und 16
Quadraten.
· Die
Zickzacklinie der DR besteht aus 8+1
Elementen.
· Der
Erweiterungsbereich des Tetraktyssterns kann auf die Erschaffung von Raum und
Zeit bezogen werden. Hexagon und äußerer Kreis als Verbundenheit von Schöpfer
und Schöpfung sind geprägt durch das Kreisflächenverhältnis 1:3. Die Schöpfung jedoch ist
zurückbezogen auf den Schöpfer durch das Flächenverhältnis 3:1.
4. Die FS der Zahlen 1-81 = 4*403. Die Einzelziffern 4 und 3 sind auf 4 Punkte und 3 Linien einer Tetraktysseite beziehbar, 4*(4+3) auf 4 Quadratseiten, wodurch dem gleichseitigen Dreieck der Tetraktys das Quadrat zur Seite gestellt wird.
Von 4+3 Elementen einer Tetraktysseite kann kein Kreisflächenverhältnis 1:3 abgeleitet werden, jedoch von 4+3 Punkten der DR:
|
|
d) 2 Primzahlreihen
in 4 Quadratrahmen
1. Die zweimal 81 Primzahlen sind in den beiden folgenden Tabellen dargestellt:
|
643 |
661 |
673 |
691 |
709 |
727 |
733 |
739 |
751 |
|
599 |
617 |
641 |
647 |
653 |
659 |
677 |
683 |
701 |
|
631 |
313 |
331 |
337 |
349 |
367 |
373 |
379 |
757 |
|
593 |
281 |
293 |
311 |
317 |
347 |
353 |
359 |
719 |
|
619 |
307 |
103 |
109 |
127 |
139 |
151 |
397 |
769 |
|
587 |
269 |
101 |
107 |
113 |
131 |
137 |
383 |
743 |
|
613 |
283 |
97 |
13 |
19 |
31 |
157 |
409 |
787 |
|
569 |
263 |
89 |
17 |
23 |
29 |
149 |
389 |
761 |
|
607 |
277 |
79 |
7 |
1 |
37 |
163 |
421 |
811 |
|
563 |
257 |
83 |
11 |
5 |
41 |
167 |
401 |
773 |
|
601 |
271 |
73 |
67 |
61 |
43 |
181 |
433 |
823 |
|
557 |
251 |
71 |
59 |
53 |
47 |
173 |
419 |
797 |
|
577 |
241 |
229 |
223 |
211 |
199 |
193 |
439 |
829 |
|
521 |
239 |
233 |
227 |
197 |
191 |
179 |
431 |
809 |
|
571 |
547 |
541 |
523 |
499 |
487 |
463 |
457 |
853 |
|
509 |
503 |
491 |
479 |
467 |
461 |
449 |
443 |
821 |
|
997 |
991 |
967 |
937 |
919 |
907 |
883 |
877 |
859 |
|
941 |
929 |
911 |
887 |
881 |
863 |
857 |
839 |
827 |
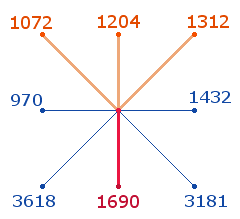
Da die Zahlensumme (ZS) der vier Achsenkreuze ohne die beiden Mittelpunktzahlen 1 und 5 durch 13 teilbar ist, bleiben diese unberücksichtigt. Die ZS der 8 Achsenarme beider Reihen (R1 und R2) sind grafisch und tabellarisch:
|
|
|
R 1 |
h. |
970 |
1432 |
2402 |
diag1 |
1072 |
1552 |
2624 |
|
|
|
v. |
1204 |
1690 |
2894 |
diag2 |
1312 |
1840 |
3152 |
|
|
|
|
2174 |
3122 |
5296 |
|
2384 |
3392 |
5776 |
11072 |
|
R 2 |
h. |
914 |
1382 |
2296 |
diag1 |
998 |
1496 |
2494 |
|
|
|
v. |
1106 |
1598 |
2704 |
diag2 |
1226 |
1736 |
2962 |
|
|
sm |
|
2020 |
2980 |
5000 |
|
2224 |
3232 |
5456 |
10456 |
|
GS |
|
4194 |
6102 |
10296 |
|
4608 |
6624 |
11232 |
21528 |
2. Als außergewöhnlich ist das Zahlenverhältnis der Mittelachsensumme zur Diagonalsumme wegen des hohen gemeinsamen Teilers und den angrenzenden Verhältniszahlen anzusehen. Es beträgt 10296:11232 = 72*13*(11:12) = 936*23 = FW 25+23 = 48.
Die geometrische Entsprechung der Zahlen 11 und 12 ist in den 2*24 symmetrischen Elementen des Tetraktyssterns zu finden:
|
|
Da der Erweiterungsring die doppelte Fläche des hexagonalen Kreises hat, sind die Einzelziffern von 11 und 12 zu lesen als 1:1 = 1:2 Kreisflächenverhältnis. Die erste Endziffer 1 ist als Ordinalzahl, die zweite Endziffer 2 als Kardinalzahl anzusehen.
Auf trinitarischer Ebene bedeutet die erste Endziffer die zweite göttliche Person, die wesensgleich aus der ersten hervorgeht, die zweite Endziffer die zweite und dritte Person.
Der gemeinsame Teiler 72 bezeichnet 24 hexagonale Elemente zu 48 Elementen des gesamten Tetraktyssterns, so daß das Verhältnis von 1:2 Elementen das Kreisflächenverhältnis 1:3 wiedergibt.
In Übereinstimmung mit diesem Zusammenhang steht der FW 48 der Gesamtsumme 21528, die sich aus 23+25 zusammensetzt. Die Einzelziffern beider Konstitutivzahlen geben das Kreisflächenverhältnis 2:1 wieder:
|
|
|
Die Analogelemente sind einmal 2:3 Radialelemente und einmal 2:5 Punkte.
Die Durchschnittszahl der 2*16 Diagonalzahlen ist 27*13 = 351 je Zahlenpaar, das ist die Summe der Zahlen 1-26.
Die Summe der 2*32 Achsenzahlen ist 21528 = 12*13*(6*23), die der übrigen 49 Zahlen 49764 = 12*13*(11*29), das Verhältnis 156*(138*319). Der gleiche Faktor 13 wird begleitet einmal durch 23 und einmal durch 29, die zusammen 52 und wiederum Teilbarkeit durch 13 ergeben. Die ZS des Wortes OPERA im SATOR-Quadrat ist aus beiden Zahlen zusammengesetzt: OP (29) ERA (23).
3. Das Verhältnis 11:12 der Summen 10296 und 11232 legt nahe, daß die beiden Primzahlreihen auf die erste und zweite göttliche Person beziehbar sind. Die beiden Summen sind:
|
|
|
Faktoren |
FW |
Faktoren |
FW |
|
R1 |
11072 |
2*2*2*2*2*2*173 |
185 |
5*37 |
42 |
|
R2 |
10456 |
2* 2* 2* 1307 |
1313 |
13*101 |
114 |
|
sm |
21528 |
|
1498 |
7*7*107 |
156 |
|
|
|
|
|
|
|
Ins Auge fällt die Gleichartigkeit der Faktoren:
·
Dem Quadrat von 8
entspricht 8 als Quadratseite.
·
Die Einzelziffern der beiden anderen Faktoren
sind gleich:
173 in der Lesart 17*3 ist auf 3 "Fischfiguren" der Tetraktys beziehbar, auf die Achsenelemente des Quadrats Qu3 und auf 17+3 Elemente des Dezimalkreises. Dem FW 185 entspricht die Numerierungssumme 18 der Eckpunkte der Tetraktys und die Numerierungszahl 5 des Mittelpunktes.
Das Ergebnis der Reihe 1 zielt auf die Tetraktys, das der Reihe 2 auf den ganzen Tetraktysstern: 13 Punkte des Tetraktyssterns und 7 Punkte des Hexagons geben das Kreisflächenverhältnis 3:1 wieder. Dasselbe Verhältnis bezeichnet der FW 1313, wenn dem Erweiterungsbereich des Hexagramms der Mittelpunkt zur Erstellung des äußeren Kreisbogens hinzugefügt wird, sowie jedem der beiden Bereiche jeweils 6 Dreiecksflächen.
Die beiden Aspekte
zweier konzentrischer Tetraktyskreise und die Tetraktys werden in den Faktoren 7*7*107 vereinigt. Zweimal 7 Punkte bedeuten das Kreisflächenverhältnis 1:3/3:1, 10 Punkte der Tetraktys und 7 Punkte des Hexagons ebenfalls das Verhältnis 3:1.
Bildet man von den FW 185 und 1313 ein weiteres Mal die FW, ist das Ergebnis 42+114 = 156 = 6*(7:19). 156 = 12*13 ist Faktor der Gesamtsumme 71292 der beiden Primzahlreihen. 7:19 bedeutet 7 Kreisflächeneinheiten für 19 DR-Punkte:
|
|
Der FW der beiden Faktoren 173+1307 = 1480 = 40*37 = 11+37 ist wiederum 48. Die Ziffern 148 sind auf die Elemente eines Quadrats beziehbar: 1 Fläche, 4 Maßeinheiten, 2 Begrenzungspunkte für jede Maßeinheit.
4. Von den Einzelsummen der beiden Reihen ist nur die Summe 1690 der ersten Reihe des unteren mittleren Achsenarmes durch 13 teilbar. Die darüber aufgefächerten 3 Achsenarme sind zusammen durch 13 teilbar:
|
|
Die Summe der drei oberen Zahlen ist 3588 = 12*13*23, ein Sechstel der Achsenzahlen. Das Zahlenverhältnis von 3:13 Achsenarmen beträgt demnach 12*13*23*(1:5).
Das Verhältnis 3:13 ist auch in der Summe 1312 erkennbar, die in ihren Einzelziffern die beiden
trinitarischen Kreisflächenverhältnisse 1:2 und 1:3 wiedergibt, also 3+4
Flächeneinheiten. Die Faktoren der Zahl 1312
sind 32*41: Aus 41
Elementen besteht das DR-Kreuz, 25 davon
gehören dem hexagonalen Bereich, 16 dem
Erweiterungsbereich an; 25:16 Elemente
bedeuten daher 1:2 Flächeneinheiten.
Die Einzelziffern der Zahl 32 sind auf 3+2 Radialelemente der DR
in der Bedeutung von 1:2 Flächeneinheiten
zu beziehen und 25 auf 2+5 Punkte der DR in
der Bedeutung von 2:1 Flächeneinheiten.
e) Zusammenschau der Zahlen
1-81 und der 2 Primzahlreihen
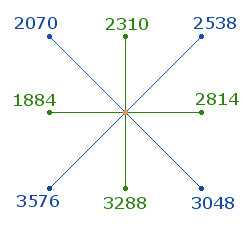
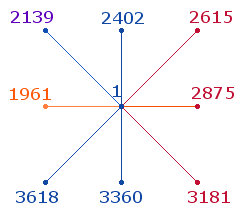
1. Ob es einen inneren Zusammenhang zwischen den FS der Zahlen 1-81 und der Summe der 81 Primzahlpaare gibt? Die folgende Grafik vereint die Summen beider Achsenzahlen:
|
|
Die Gesamtsumme beträgt 22152 = 24*13*71 >FW 93 =3*31. Keine einzelne Summierung ist durch 13 teilbar, jedoch die drei rechten Zahlen zusammen: Die Summe 8671 = 13*23*29 >FW 65 vereinigt die drei zweistelligen Faktoren, die mehrfach schon in Kombination aufgetreten sind.
Die drei rechten Zahlen stellen eine Quadrathälfte ohne vertikale Mittelachse dar. Die Summe der sechs anderen Zahlen beträgt 13481 = 13*17*61 >FW 91. Die FW beider Summen sind durch 13 teilbar und ergeben 65+91 = 156 = 12*13. Von Interesse ist der Faktor 61, der in der Gesamtsumme 76128 der 169 Primzahlen von 1-1000 enthalten ist.
Eine Sonderrolle nimmt der Faktor 23 ein:
·
Die Faktoren der mittleren Zahl 2875 sind 5³*23.
Mit den anderen beiden Zahlen bildet sie das Verhältnis 2875:5796 = 23*(125:252) = 23*377 =
23*(13*29).
·
Beide Einzelsummen der linken oberen Zahl 2139 sind durch 23
teilbar: 69+2070 = 3*23*(1+30) = 69*31 = 23*93.
8671+2139
ergibt 10810 = 10*23*47.
·
Die Zahl 2875
sorgt durch Addition mit 1961 für eine
zweite durch 13 teilbare Summe: 4836 = 12*13*31. Es ist dieselbe Summe wie die der
5 überzähligen Primzahlen + der Primzahlen 2 und 3.
2. Die Gesamt-FS der Zahlen 1-81 und der 81 Primzahlpaare beträgt 1612+71292 = 72904 = 8*13*701 = FW 720 >12+7 = 19. In ihren Einzelziffern gesehen bedeutet 701 7+1 Punkte der DR, 1 ist als zweiter Mittelpunkt zu verstehen. 12+7 Punkte der DR geben 4+3 Kreisflächeneinheiten wieder, 13:8 Elemente der DR das Kreisflächenverhältnis 1:2.
3. Ähnlichkeiten zu den quadratischen Ergebnissen zeigen sich, wenn man alle 169 Primzahlen von 1-1000 und die FS der Zahlen 1-81 addiert: 76128+1612= 77740 = 4*5*13*13*23. Das Verhältnis der 36 Zahlen der drei rechten Achsenarme zur Summe der 207+7 übrigen Zahlen beträgt daher 8671:69069 = 13*23*(29:231) und das Verhältnis der 64 Achsenzahlen der 81 Primzahlpaare zu den 179+7 übrigen Zahlen 21528:56212 = 4*13*23*(18:47).
Die Zahlen 13 und 23 sind besonders auf Entsprechung der Radialelemente und Durchmesserelemente der DR zu den Kreisflächenverhältnissen 1:2 und 1:3 zu beziehen: (3+2)+(3+5) = 5+8 = 13; (5+4)+(5+9) = 9+14 = 23. Die Summe von 13 Radialelementen gilt für beide Radialhälften, was sich im Faktor 13² der Gesamtsumme 77740 zeigt. Die zweimal 13 Radialelemente fallen zusammen mit der Zahl der 26 Elemente des Oktaeders.
Dem Produktergebnis 13*23 = 299, aufgeteilt in 29+9, entspricht die Numerierungssumme von 1-5 vom Mittelpunkt der DR an zum Rand von 9 Durchmesserelementen:
|
|
Aufgeteilt in 2*(9+9) oder 29+9 ist 299 auf ein DR-Kreuz beziehbar, aus dem sich ein Oktaeder zusammenfügen läßt: Der DR-Rahmen besteht aus zwei Durchmesserlinien von je 9 Elementen, der Rahmen eines DR-Kreuzes aus 29 Elementen; die einzelne 9 kann als Ausgangszahl von 9 Durchmesserelementen interpretiert werden.
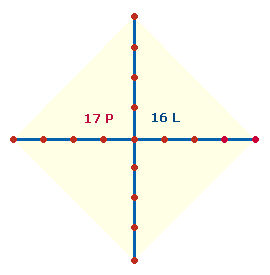
4. Die 33 Achsenzahlen der Zahlen 1-81 lassen sich auf einem einfachen Achsenkreuz von der niedrigsten zur höchsten in Vierer-Einheiten rundum anordnen. Dabei gibt es Additionsergebnisse für die Zahlen auf Punkten und auf Linien. Das unnumerierte Grundmodell hat folgende Gestalt:
|
|
Die Rundumnumerierung ist im folgenden in vier Tabellenzeilen dargestellt. Die 1 des Mittelpunktes ist dabei zunächst nicht berücksichtigt:
|
2 |
6 |
11 |
19 |
28 |
40 |
53 |
69 |
228 |
2 |
5 |
11 |
19 |
11 |
11 |
53 |
26 |
138 |
|
4 |
8 |
15 |
23 |
34 |
46 |
61 |
77 |
268 |
4 |
6 |
8 |
23 |
19 |
25 |
61 |
18 |
164 |
|
3 |
7 |
13 |
21 |
31 |
43 |
57 |
73 |
248 |
3 |
7 |
13 |
10 |
31 |
43 |
22 |
73 |
202 |
|
5 |
9 |
17 |
25 |
37 |
49 |
65 |
81 |
288 |
5 |
6 |
17 |
10 |
37 |
14 |
18 |
12 |
119 |
|
|
30 |
|
88 |
|
178 |
|
300 |
596 |
|
24 |
|
62 |
|
93 |
|
129 |
308 |
|
14 |
|
56 |
|
130 |
|
236 |
|
436 |
14 |
|
49 |
|
98 |
|
154 |
|
315 |
|
1032
= 2*12*43 = 2*516 |
1032 |
308:315 = 7*(44:45) |
623 |
||||||||||||||
|
216:300 = 12*(18:25); 192:324 = 12*(16:27) |
|
147:168
= 21*(7:8) |
|||||||||||||||
|
408:624 = 24*(17:26) |
|
376+1:247
= 13*(29:19); 233+1:390 = 78*(3:5) |
|||||||||||||||
Die Zahlen sind jeweils von innen nach außen angeordnet: Horizontalachse links, rechts, Vertikalachse oben, unten.
Die Summen der Punktezahlen und Linienzahlen stehen jeweils in der oberen und unteren Tabellenzeile. Die ZS und FS befinden sich in der linken und rechten Hälfte der Tabelle.
Jeweils zwei ZS der Punkte und Linien lassen sich zweimal zur halben Gesamtsumme 516 zusammensetzen.
Für die FS der Punkte und Linien sind – ohne Mittelpunkt-1 – Teilbarkeit durch 7 kennzeichnend. Die vier Liniensummen sind jeweils einzeln durch 7 und in zwei konzentrischen Paaren durch 21 teilbar. Unter Hinzufügung der Mittelpunkt-1 sind zwei oder mehr Verhältnisse mit Teilbarkeit durch 13 möglich.
Die Gesamt-ZS+FS beträgt 1033+624 = 1657, eine Primzahl. Die Einzelziffern 1+6 und 5+7 sind zweimal auf die Punkte der DR zu beziehen, sie geben 3+4 oder 4+4 Kreisflächeneinheiten der beiden Tetraktyskreise wieder.
5. Das erstellte Achsenkreuz läßt sich um 32 Primzahlpaare erweitern. Die Abfolge von Linien und Punkten ist dieselbe:
|
18 |
78 |
162 |
330 |
534 |
822 |
1170 |
1584 |
4698 |
|
42 |
114 |
240 |
408 |
666 |
966 |
1362 |
1800 |
5598 |
|
30 |
90 |
204 |
372 |
594 |
900 |
1242 |
1686 |
5118 |
|
60 |
126 |
288 |
462 |
738 |
1050 |
1452 |
1938 |
6114 |
|
|
408 |
|
1572 |
|
3738 |
|
7008 |
12726 |
|
150 |
|
894 |
|
2532 |
|
5226 |
|
8802 |
|
|
|
8736 |
|
|
21528 |
|||
Wieviele durch 13 teilbare Verhältnisse möglich sind, kann ich nicht sagen. Eine konzentrische Paarung der Außen- und Innenglieder ergibt 12792:8736 = 312*(28:41). 5226 ist allein durch 13 teilbar, wodurch das Binnenverhältnis 5226:7566 = 78*(67:97) zustande kommt.
Die Summen der 33+32 Achsenzahlen lassen sich untereinander schreiben: 832+1634+7137
|
|
408 |
|
1572 |
|
3738 |
|
7008 |
|
150 |
|
894 |
|
2532 |
|
5226 |
|
|
|
24 |
|
62 |
|
93 |
|
129 |
|
14 |
|
49 |
|
98 |
|
154 |
|
|
|
432 |
|
1634 |
|
3831 |
|
7137 |
|
164 |
|
943 |
|
2630 |
|
5380 |
|
Drei gemeinsame Punktesummen +1 ergibt das Verhältnis 9204:12948 = 156*(59:83) = 312*71 = 22152. Weitere Verhältnisse müßten gesucht werden.
Erstellt: Juni 2016, Oktober 2018