|
s.a. Zyklische
Zahlen |
Zwei Primzahlmuster
|
|
Primzahlmuster 1
a) Grundlegung
c) Reduktionen
Einleitung
Die
Zahlen des Dezimalsystems sind einem lebendigen Organismus
vergleichbar, der durchzogen wird von Strukturprinzipien und Bauelementen. Dazu
gehören auch die beiden zu untersuchenden Primzahlmuster.
Ist 1 eine Primzahl? Es herrscht
in der Mathematik die Übereinkunft, die Zahl 1 nicht zu den Primzahlen zu
rechnen, da sonst bei weiteren Definitionen stets auf die Zahl 1
als Ausnahme verwiesen werden müßte. Eine Übersicht über das Problem ist bei Wikipedia zu finden. Es sind somit nicht prinzipielle, sondern
praktische Gründe, die Zahl 1 von den Primzahlen
auszuschließen. Prinzipiell gilt also: Die Zahl 1 ist eine Primzahl. Wie
sollte man auf die Zahl 1 verzichten, aus der alle
anderen Zahlen hervorgehen? Ohne den Baustein der Primzahl 1
würde das Ordnungsgebäude der Primzahlen nur unvollständig erkannt werden. Nur
so tritt z.B. das den drei Musterreihen analoge Verhältnis von 15:30:15 Primzahlen der ersten 300-er Einheit in Erscheinung (mehr
dazu unter PZ 1-900).
Siehe auch: Warum 1 eine
Primzahl ist.
Erstes Primzahlmuster
a) Grundlegung
1.
Primzahlen
sind immer ungerade. Laut Definition sind sie nur durch sich selbst und durch 1
teilbar. Alle anderen Zahlen sind aus zwei oder mehr Faktoren zusammengesetzt.
Zur Bestimmung von Primzahlen fallen also alle geraden und somit durch 2 teilbaren Zahlen außer der Zahl 2 selbst weg.
Die Zahl 5
ist die Hälfte des dezimalen Zyklus von je 10 Zahlen und ist als Endziffer stets durch sich selbst
teilbar. Als Positionen für Primzahlen kommen also die Endziffern 1 3 7 9 in Frage.
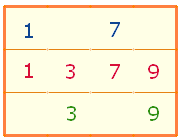
Bildet man mit der Zahl 3
eine Multiplikationsreihe von 1-9,
werden 4
ungerade Endziffern besetzt:
|
Reihe 1 |
1 |
1*3 |
7 |
3*3 |
|
Reihe 2 |
1 |
3 |
7 |
9 |
|
Reihe 3 |
7*3 |
3 |
9*3 |
9 |
Die Multiplikationen fallen in je zwei
ungerade Ziffern der ersten und der dritten Dekade, während die zweite Dekade unverändert 4 mögliche
Primzahlpositionen aufweist.
Jede der 4
ungeraden Ziffern ist nun zweimal vertreten, ihre Summe ist 2*20 = 40. Von den ersten 30 Zahlen kommen also nicht mehr als 8 Zahlen als
Primzahlen in Frage. Das Verhältnis der 4
Endziffern in den 3 Reihen ist 2:4:2 = 2*(1:2:1).
|
Reihe 1 |
1 |
– |
7 |
– |
|
Reihe 2 |
11 |
13 |
17 |
19 |
|
Reihe 3 |
– |
23 |
– |
29 |
Die Tabelle zeigt 4 komplementär einander zugeordnete Paare, z.B. 1+29, deren Addition jeweils 30, zusammen 120
ergibt.
Wenn alle PZ-Positionen mit
Primzahlen besetzt sind, gilt für jede 30-er Einheit die mittlere Zehnerzahl
mal 8 + 40,
z.B. zwischen 31 und 59: 8*40
= 320+40 = 360. Da PZ-Position 49
ausfällt, ist die PZ-Summe 311. Jede neue 30-Einheit nimmt
um 240 zu, also 360+240 = 600 zwischen 61
und 89, es fällt 77 heraus, die PZ-Summe ist
523. Für die ersten 100
Zahlen ergibt sich somit nach 30-er Einheiten die Addition 120+311+523+97 = 1051, mit 2+3+5
1061. Beide Summenzahlen sind prim.
2.
Dieses grundlegende Primzahlmuster kommt dadurch zustande,
daß die Zahlen 2,
3 und 5 "ausgesiebt" werden, wobei 5 bereits eine
Addition von 2+3 ist. Gemeinsam ist ihnen,
daß ihre mindestens einmalige Verdoppelung innerhalb der ersten Zehnereinheit erfolgt. Die bei der Aussiebung
herausfallenden Summen von der Gesamtsumme 55 sind 2+4+6+8+10 = 30, 3+9 = 12
und 5, zusammen 47, es bleiben 1 und 7
übrig. Läßt man die drei Ausgangszahlen 2+3+5 = 10 weg, ist die Addition 28+9+0 = 37. Dieses Ergebnis ist zweifach auf die Tetraktys
beziehbar:
·
Die 37 Elemente der Tetraktys teilen sich
auf in 10 Punkte +
18 Linien und 9 Dreiecke.
·
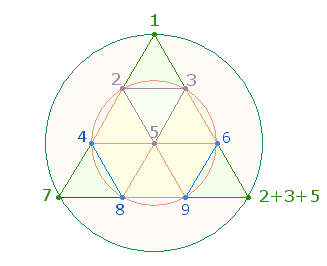
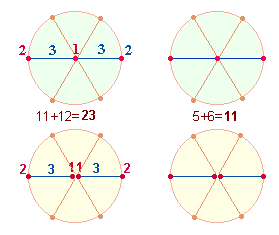
Bei Numerierung der 10
Punkte befinden sich 1+7+(2+3+5) auf den
erweiterten 3 Eckpunkten und die übrige
Summe 37 auf den 7
hexagonalen Punkten:
|
|
Die Zahl 10 ist also gewissermaßen die Wiederholung und Zusammenfassung der Primzahlen 2+3+5. Es zeigt sich, daß neben 2, 3 und 5 auch die anderen Zahlen durch 2 und 3 dargestellt werden können: 4+6 = 2*(2+3), 8 = 2³, 9 = 3², 1+7 = 8 = 2³; 27+8 = 3³+2³. Fügt man die hexagonalen 2+3+5 zu der Eckpunktsumme 18 hinzu, ergibt sich die Summe der Zahlen 1-7 = 28 und die Summe 8+9+(4+6) für die restlichen 3 Zähler.
3.
Lücken
im PZ-Muster treten dort auf, wo eine PZ-Position durch ein Produkt aus zwei oder mehr Primzahlen eingenommen wird. Die folgende Tabelle
zeigt, wie eine Primzahl nach der anderen, beginnend von ihrem eigenen Quadrat, Produkte
mit fortlaufend höheren Primzahlen
bildet, z.B. 7*11 und damit eine PZ-Position unbesetzt bleibt.
Die oberste Reihe der folgenden Tabelle enthält 14 Nicht-Primzahlen
auf PZ-Positionen:
|
49 |
77 |
91 |
119 |
121 |
133 |
143 |
161 |
169 |
187 |
203 |
209 |
217 |
221 |
|
7 |
7 |
7 |
7 |
|
7 |
|
7 |
|
|
7 |
|
7 |
|
|
7 |
11 |
13 |
17 |
|
19 |
|
23 |
|
|
29 |
|
31 |
|
|
|
|
|
|
11 |
|
11 |
|
|
11 |
|
11 |
|
|
|
|
|
|
|
11 |
|
13 |
|
|
17 |
|
19 |
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
17 |
Das Muster aus 3 Zehnereinheiten beginnt von
neuem nach 10*3 Einheiten. Es endet mit der Zahl 300 und beginnt von neuem mit der Zahl 301. Siehe dazu Die Primzahlen von
1-1000 mit Anordnung der Primzahlen in 30-er Einheiten.
4. Zwischem dem Ende und Anfang
zweier 30-er Einheiten liegen zwei aufeinander folgenden PZ-Positionen, denen eine
Verbindungsfunktion zugewiesen werden kann. Wird eine der beiden oder beide
Positionen nicht durch Primzahlen besetzt, wird eine Kette von 30-er Einheiten
unterbrochen. Dies geschieht z.B. durch die Zahlen 91 und 119/121. Den 3:1 30-er Einheiten (1-90, 91-120) gehören 22+6 Primzahlen an, deren Summen
945 und 630 das Verhältnis 18*(53:35) haben.
Die 30-Einheiten bilden also
zwei Gruppen von verbundenen und unverbundenen Einheiten. Letztere nehmen
stetig zu. Zwischen 1 und 990
gibt es 11
Primzahlzwillinge mit Verbindungsfunktion:
|
29 |
59 |
149 |
179 |
239 |
269 |
419 |
569 |
599 |
659 |
809 |
3979 |
|
31 |
61 |
151 |
181 |
241 |
271 |
421 |
571 |
601 |
661 |
811 |
4001 |
|
7980 = 19*20*21 = 210*38 |
7980 |
||||||||||
Die Primzahlen 991 und 997 werden an die PZ-Zwillinge 1019 und 1021 angebunden. Die Summe der 164 Primzahlen (ohne 2 3 5) beträgt 74130 = 210*353.
Fügt man zur Gesamtsumme die
Primzahlen 2+3+5
hinzu, enthält das Produkt 10*29*31 die beiden Primzahlen, die die ersten zwei 30-er
Einheiten verbinden.
Das Verhältnis der 11 Primzahlzwillinge zu den
insgesamt 33
30-er Einheiten ist 11*(1:2).
Das Verhältnis der
verbundenen zu den unverbundenen Primzahlen ist 100:64 = 4*(25:16).
5. Jede
300-er Einheit enthält 80
Primzahlpositionen in der Hunderterfolge 26+28+26. Für die Zahlen 1-1000 ergeben
sich daher 3*80+26 = 266 PZ-Positionen. Davon sind 166
Primzahlen und 100
Primzahllücken, 10
je Hundert. Alle
Lückenzahlen bestehen aus Produkten von
Primzahlen. Die unterste Primzahl 7 und sieben weitere wandern
durch die aufsteigende Reihe der Primzahlen bis zu dem Produkt, das als letztes
unter 1000
liegt. Die letzte Primzahl 31 kann nur noch das Quadrat mit sich selbst bilden:
|
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
150 |
|
139 |
89 |
73 |
53 |
47 |
43 |
31 |
31 |
506 |
|
31 |
20 |
16 |
10 |
8 |
6 |
2 |
1 |
94 |
|
506 = 11*46 |
||||||||
Die zweite Reihe zeigt die jeweils
höchste Primzahl, die unterhalb 1000 ein Produkt mit der Primzahl der ersten Reihe bilden kann. Die dritte Reihe zeigt die Zahl der
Primzahlen zwischen der Zahl der ersten und zweiten Reihe.
6 Produkte bestehen aus drei Primzahlen:
|
343 |
539 |
637 |
833 |
847 |
931 |
4130 |
|
7*7*7 |
7*7*11 |
7*7*13 |
7*7*17 |
7*11*11 |
7*7*19 |
166 |
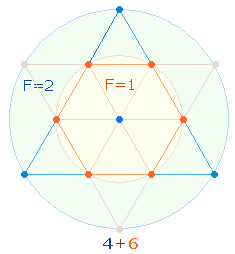
Die Zahl 7 bildet also 31+6 = 37 Produkte. Die Einzelziffern
geben ein Verteilungsmuster der 10 Tetraktyspunkte wieder:
|
|
4:6 Punkten entspricht das Kreisflächenverhältnis 3:1. 4:6 beträgt auch das Verhältnis
der inneren vier zu den äußeren vier Primzahlmengen: (26+14):(57+3).
Weitere
Details finden sich im Kapitel Die
Zahlen 1-1000.
6.
Seit der
Veröffentlichung dieses Beitrags sind neun Jahre vergangen. Mittlerweile
scheint eine früher verbreitete irrationale Haltung zu den Primzahlen im
Schwinden begriffen zu sein. Die Abfolge der Primzahlen wird nun auch von den Primzahllücken her wahrgenommen, die gemäß einem klar
definierten Primzahlmuster entstehen. Computerdarstellungen sind dabei eine
große Hilfe.Tatsächlich scheint früher kaum jemand über das "Sieb des
Eratosthenes" hinaus gedacht zu haben. Denn dieses Sieb setzt sich endlos
fort. Man müßte also von einem "Sieb des Eratosthenes plus" sprechen.
1. Das ermittelte Primzahlmuster wiederholt sich
nach jeweils 30 Zahlen. Es läßt klar erkennen, wieviele
Primzahlen und an welcher Stelle in einer Zehnerreihe maximal zu erwarten sind.
Das vorliegende
Primzahlmuster schafft einige rationale Klarheit. Die Frage stellt sich jedoch,
handelt es sich um eine Abstraktion menschlichen Denkens, oder kommt ihm
wesentliche, d.h. letztlich ontologische Bedeutung zu? Um diese Frage zu
klären, ist die Einbeziehung von Faktorenwerten (FW) unerläßlich.
2.
Eine
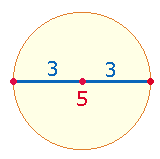
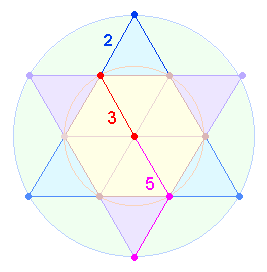
wesentliche Bedeutung der Zahlen 1-30 besteht
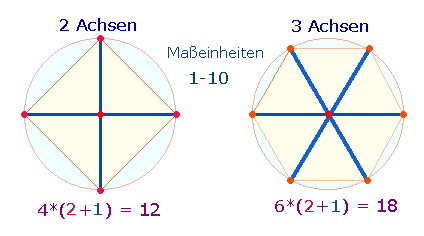
darin, daß 10 Maßeinheiten (Linien) von je 2 Punkten begrenzt werden, wie dies durch zwei
Radien eines Kreises
vorgebildet ist. Als geometrische Modelle sind die 2 Achsen des Achsenkreuzes und 3 Achsen
des Hexagons anzusehen:
|
|
Eine Achse besteht aus 2+3 = 5 Elementen, zwei Radien aus 3+3 = 6 Elementen. Dies drückt sich sinnfällig
in der Zahlensumme (ZS) + Faktorensumme (FS) der Zahlen 1-30 aus: 465+294 = 759 = 23*33.
Die FW der 30 Zahlen sind:
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
sm |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
465 |
|
P |
1 |
|
3 |
4 |
|
5 |
7 |
|
6 |
7 |
|
7 |
13 |
|
8 |
8 |
|
8 |
19 |
|
10 |
13 |
|
9 |
10 |
|
9 |
11 |
|
10 |
168 |
|
L |
|
2 |
|
|
5 |
|
|
6 |
|
|
11 |
|
|
9 |
|
|
17 |
|
|
9 |
|
|
23 |
|
|
15 |
|
|
29 |
|
126 |
|
126:168 = 42*(3:4) |
294 |
||||||||||||||||||||||||||||||
Die Zuordnung von je zwei
Punkten zu einer Maßeinheit wird durch das FaktorenSummen-Verhältnis
3:4 bestätigt.
Je drei FW für eine Maßeinheit
ergeben folgende FS:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
|
9 |
10 |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
6 |
14 |
19 |
25 |
30 |
33 |
38 |
45 |
34 |
50 |
||||||||||||||||||||
Die Mitte der Skala bilden
die Maßeinheiten 5 und 6 mit den FS 30+33 = 3*(10+11) =
63. Sie sind konzentrisch umgeben von 4 und 7
mit derselben FS 63 (25+38), so daß die FS 126 dieser 4 Maßeinheiten zur
restlichen FS 168 von 6
Maßeinheiten das Verhältnis 42*(3:4) ergibt.
3. Die ZS+FS der
Zahlen 1-30 ist 465+294 = 759 = 3*(11*23). Die Zahl 3 bezieht sich auf drei Achsen des
Hexagon und der Doppelzählung von numerierten und unnumerierten Radial- und
Durchmesserelementen:
|
|
1. Die Existenz eines
unveränderlichen Primzahlmusters hilft, die ins Endlose wachsenden Zahlen immer
wieder auf grundlegende Zahlenverhältnisse zu reduzieren – sofern logisch
stimmige Zahleneinheiten gewählt werden. Die Ausgangsverhältnisse sind stets
die beiden Kreisflächenverhältnisse 1:2 und 1:3 bzw. deren Umkehrungen.
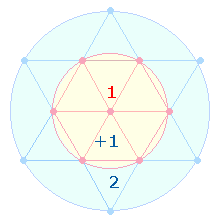
2. Das Ausgangsverhältnis des
Primzahlmusters ist 8 PZ-Positionen zu 22 übrigen Zahlen, also das Verhältnis 8:22 bzw. 22:8.
Der
FW von 22 ist 2*11
= 13. Die Einzelziffern von 2*11
kennzeichnen bereits das Kreisflächenverhältnis (2+1):1 = 3:1:
|
|
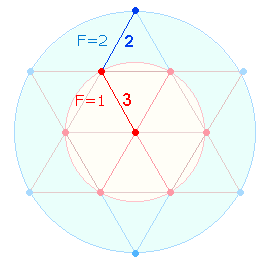
Die
Bedeutung ändert sich, wenn man die Einzelziffern der Zahl 22
hinzunimmt: Die Zahl 3 und einmal 2 beziehen sich nun auf die
Radialelemente, die die Flächeneinheiten 1
und 2 wiedergeben:
|
|
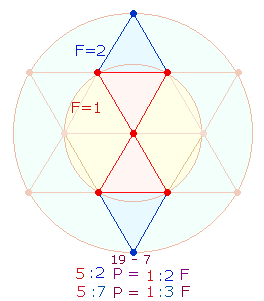
Ein
weiterer Aspekt kommt durch die Addition 22+13
= 35 hinzu. Die Einzelziffern bezeichnen nun 3
und 5 Radialelemente des hexagonalen inneren Kreises und des
ganzen äußeren Kreises in der Bedeutung von 1:3 Flächeneinheiten. Dieselbe
Bedeutung haben auch die Faktoren 5*7 der Zahl 35.
Bezugspunkt sind die 7 Punkte der Doppelraute: 5
Punkte gehören dem hexagonalen, 2 dem Erweiterungsbereich
zu:
|
|
Die
Rahmenelemente ermöglichen die Reduktion von 8+22
auf die Einzelziffern 8+(2+2), auf 8
Linien und 2+2 Querpunkte; die 9 vertikalen
Elemente sind dabei nicht berücksichtigt.
Der
FW von 8
ist 6,
das FW:ZW-Verhältnis 2*(3:4).
Das interne Differenzverhältnis der Verhältniszahlen ist 3:1.
3. Weitere Auskunft gewinnen
wir durch die Hinzufügung der FW:
|
ZW |
FW |
sm |
FW |
|
22 |
13 |
35 |
12 |
|
8 |
6 |
14 |
9 |
|
30 |
19 |
49 |
21 |
|
49:21 = 7*(7:3) |
|||
Die
Summe 35+14 = 49 ergibt die Zahl der Elemente des
Tetraktyssterns. Das entsprechende Verhältnis 7*(5:2)
kann auf je 7 Punkte eines DR-Kreuzes bezogen werden, das zu
einem Oktaeder
zusammengefügt werden kann. Das Verhältnis 7*(7:3)
bezieht sich auf die 7 Punkte des Hexagons und 7+3
Punkte der Tetraktys und gibt das Kreisflächenverhältnis 1:3 der
beiden Tetraktyskreise wieder.
4. Sofern die logischen
Ordnungsstrukturen des Dezimalsystems eingehalten werden, führen
Zahlenergebnisse auf ihr Zentrum zurück, d.h. zu Zahlen, die nicht mehr als
etwa vier Stellen umfassen und somit interpretierbar sind. Dies gilt für endlos
hohe Zahlen. Möglich sind Reduktionen durch Zahlenverhältnisse. Das
Grundverhältnis besteht in der Dualität von Zahlensummen (ZS) und Faktorensummen
(FS). Die Reduktion geschieht
durch die Verrechnung von ZS und FS.
5. In der Betrachtung der
Zahlen von 1-1000
liegen drei ZS
und drei FS vor.
Es handelt sich um die ZS und FS von 169 Primzahlen, 100 Zahlen auf
Primzahlpositionen und 731 übrigen Zahlen. Sie können in
verschiedener Weise einander zugeordnet werden. Hier sollen ihre Faktorenwerte (FW) ermittelt werden:
|
|
ZS |
sm |
FS |
sm |
GS |
||||
|
|
169 |
100 |
731 |
|
169 |
100 |
731 |
|
|
|
|
76128 |
56550 |
367822 |
500500 |
76128 |
6012 |
60568 |
142708 |
643208 |
|
FW |
87 |
57 |
112 |
256 |
87 |
177 |
186 |
450 |
706 |
|
706
= 2*353 = FW 355 |
|||||||||
Durch
die Ermittlung der FW wird die Gesamtsumme 643208
auf 706 reduziert.
Die Einzelziffern der Primzahl 353 kann zweifach
interpretiert werden:
·
Als 5
Durchmesser- und 3+3 Radialelemente der
Kreisachse:
|
|
·
Als Kontraktion von 3+5/5+3 beziehen sie sich
auf die bereits oben erwähnten Radialelemente des Doppelkreises des
Tetraktyssterns in der Bedeutung von 1:3/3:1 Flächeneinheiten:
|
|
6. Die Faktoren der Gesamt-FS 142708 sind 2²*35677 = FW
35681, die
Faktoren der Gesamt-ZS 500500
sind 2²*5³*7*11*13
= FW 50. Die
Primzahl 35677 ist zwar interpretierbar als 356 und 677, aber eben doch 5-stellig. Ihre Reduktion gelingt
erst durch die ZW/FW-Verrechnung:
|
|
ZS |
FS |
sm |
FW |
|
|
500500 |
142708 |
643208 |
137 |
|
FW |
50 |
35681 |
35731 |
35731 |
|
sm |
|
|
|
35868 |
|
643208 = 2³*37*41*53
> 137 |
||||
|
35868 = 21*28*61 = FW 10+11+61 = 82 |
||||
Ebenfalls auf 137 reduzieren sich die zwei 9-stelligen Kaprekar-Konstanten: 554999445 = 34* 5* 7* 11* 13* 37* 37 > 122 und 864197532 = 2²*3³* 11* 181* 4019 > 4224:
|
|
|
|
sm |
FW |
|
Zahl |
554999445 |
864197532 |
1419196977 |
4778461 |
|
FW |
122 |
4224 |
4346 |
96 |
|
sm |
|
|
|
4778557 |
|
4346 = 2*41*53; 4778557 = 7* 19²* 31* 61 >137 |
||||
Die Primzahl 137 ist insbesondere als 13:7 zu lesen: Der Tetraktysstern besteht aus 13 Punkten, das darin enthaltene Hexagon aus 7. Schlägt man um das Hexagramm einen Kreis so geben 13:7 Punkte das Kreisflächenverhältnis 3:1 wieder.
7. Die Dreiteilung der Zahlen
in Primzahlen, Zahlen auf Primzahlpositionen (Lückenzahlen) und übrige Zahlen
sowie die Ermittlung ihrer Faktorenwerte ermöglicht eine Verfolgung ihrer
allmählichen Verschiebung: Die FS der übrigen Zahlen wird die FS der ersten beiden Gruppen aufgrund stetiger Abnahme der Primzahlen
irgendwann einholen. Dasselbe gilt für die Lückenzahlen gegenüber den
Primzahlen sowohl hinsichtlich der ZS als auch der FS.
Erstellt:
Februar 2006
Überarbeitet:
Oktober 2010, August 2015