Die Zahl 83 und 830
Verse der 10 Eklogen
I. Zahlensummen
III. Die 10
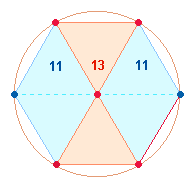
Verszahlen im Kreismodell
IV. 415 und
830
I. Zahlensummen
1.
Von den 10 Eklogen ist nur die Verszahl
der 8. Ekloge umstritten. Eine formale Analyse des
Textes zeigt, daß die Zahl von 109 Versen der meisten Ausgaben auf 110 korrigiert werden muß.
Die Zehnzahl der
Eklogen legt nahe, daß Vergil die Verszahlen nach Strukturen des Dezimalsystems
bestimmt hat, dem hauptsächlich drei Modelle zugrunde liegen: das Streckenmodell, das Kreismodell und das Tetraktysmodell. Als unerläßlich kommen
die Faktorenwerte (FW)
der Verszahlen hinzu.
2.
Die Verszahlen der 10 Eklogen sind:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
55 |
|
ZS |
83 |
73 |
111 |
63 |
90 |
86 |
70 |
110 |
67 |
77 |
830 |
|
|
420 |
410 |
|
||||||||
Zu den Verszahlen
sind zunächst vier Einzelbeobachtungen zu machen, die sicherlich beabsichtigt
sind, aber nicht im einzelnen gedeutet werden sollen:
–
Die
Teilung der 10 Eklogen in 420
und 410 Verse erfolgt in angrenzenden Zehnereinheiten.
–
Die
Verszahlen 83, 73 und 67 sind Primzahlen. Weitere drei Verszahlen sind
Zehnerzahlen: 90, 70, 110.
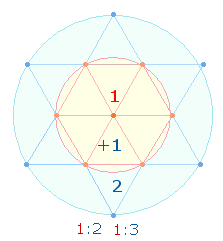
–
Die
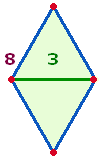
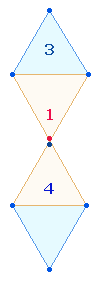
Ziffern 2, 4, 5 sind in den Verszahlen nicht
berücksichtigt. Die drei Ziffern sind Elemente der Raute: 2 Flächen, 4
Punkte, 4+1
Linien. 8 Rahmenelemente umschließen 3 Binnenelemente:
|
|
Die Summe der 6 übrigen Ziffern von 1-9
beträgt 44. Wie am Ende dieser Ausführungen
noch zu zeigen sein wird, könnte die so gegliederte Raute das Grundthema von
Vergils Konstruktion sein.
–
Die
Addition der Einzelziffern ergibt, von den Einer- bis Dreierstellen 30, 60 und 2, zusammen 92.
3.
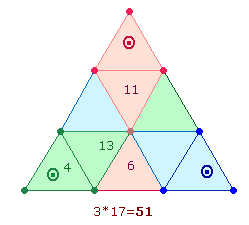
Es ist gleich erkennbar, daß die erste
Ekloge mit 83 Versen den 10. Teil der Gesamtzahl 830 ausmacht und damit
den thematischen Auftakt bildet. Da die 2., 5. und 6. Ekloge zusammen zu einer Einheit aus 3*83 Versen gruppiert
sind, ergibt sich eine numerische Gliederung aus 1+3+6 Eklogen, die auch der
Tetraktys zugrunde liegt: Mittelpunkt, 3 Eckpunkte, 6 Kreislinienpunkte.
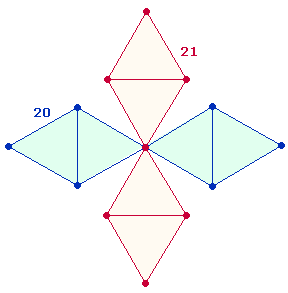
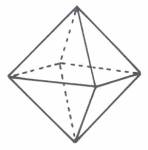
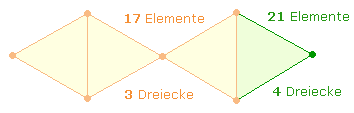
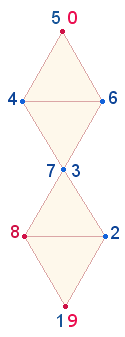
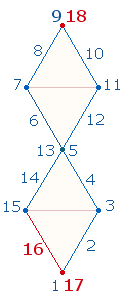
Die Konstitutivzahlen der Primzahl 83 sind 42+41. Sie beziehen sich auf ein Achsenkreuz aus zwei Doppelrauten (DR)
zu je 21 Elementen, die zu einem Oktaeder
zusammengesetzt werden können. Das erste
Achsenkreuz besteht aus 41 Elementen, beim zweiten sind für beide DR
jeweils 21
Elemente zu zählen:
|
|
|
4.
Eine wesentliche Bedeutung der Verszahlen 83 und 73 der ersten und zweiten
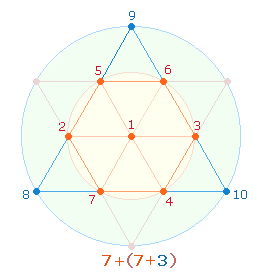
Ekloge ergibt sich aus den 7 Punkten des Hexagons und den 10
Punkten der Tetraktys:
|
|
Die Zahl 83 setzt sich zusammen aus den Summen der Zahlen 1-7 = 28 und 1-10 = 55, die Zahl 73 aus den zugehörigen Faktorensummen (FS) 27+46. Die 7 Punkte des Hexagons und 10 Punkte der Tetraktys geben das Kreisflächenverhältnis 1:3 wieder.
Die Bezogenheit der
Verszahlen auf 7 Punkte des Hexagons, 3 Erweiterungspunkte und die Gesamtheit von 10 Punkten zeigt sich
deutlich an den Einerstellen:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
83 |
73 |
111 |
63 |
90 |
86 |
70 |
110 |
67 |
77 |
Die Einerstellen sind
dreimal 3, zweimal 7 und einmal aus 1+6 zusammengesetzt. Es
bleiben drei 0-Stellen übrig, die als Multiplikationsfaktor 10 der Zehnerstellen zu verstehen
sind. Es ergeben sich so durch die Summen 270 und 560 zwei durchschnittliche Verszahlen je Ekloge:
für die drei 10-er Zahlen 90, für die übrigen sieben 80, die sich durch die Verszahlen 83+77 = 160 in 2:5 Verssummen unterteilen: 111+86+63 = 260; 67+73 = 140; 260:140 = 20*(13:7);
160:400 = 80*(2:5).
Die Zahlen 7 und 10 sind auch auf 7 Punkte und 10 Linien der Doppelraute beziehbar.
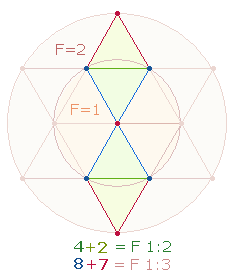
5.
Die Summe 83+73 = 156 ergibt das Produkt 12*13. Der Faktor 13 ist aus zwei Gründen für den Tetraktysstern
relevant: Erstens, der Tetraktysstern besteht aus 13 Punkten, zweitens, das Kreisflächenverhältnis des inneren zum
äußeren Kreis ist 1:3, das des inneren
Kreises zum äußeren Kreisring 1:2. Mit diesen beiden Verhältnissen stimmen die
Einzelziffern der Faktoren 12*13 der Zahl 156 überein:
|
|
156 kann sich in der
Aufteilung von 15 Rahmenelementen und 6 Binnenelementen auf die 21 Elemente der DR
beziehen. Die folgende Aufteilung von Elementen gibt die beiden
Kreisflächenverhältnisse wieder:
|
|
6.
Beim gewöhnlichen Zählen achtet man nicht
darauf, ob es sich um 5 Zentimeter oder 5 Münzen handelt, also um Maße oder
Gegenstände. Beim Betrachten von geometrischen Figuren erkennt man, jedoch daß
jede Linie durch zwei Punkte begrenzt ist. Zwei 5-er Einheiten in einer
geometrischen Figur bedeuten also, daß nebeneinander jeweils 3 Punkte 2 Maßeinheiten
begrenzen. Dies ist in der DR durch zweimal 5 Radialelemente der Fall:
|
|
|
Beide Figuren geben
Eigenschaften des OKTAEDERS wieder: Ein äußerer Punkt und ein Mittelpunkt stellen eine obere und untere Ecke dar, zwei Querpunkte mit Linie die Mittelbasis von oberer und unterer
Pyramide, 8 Dreiecksflächen des
DR-Kreuzes die Flächen des Oktaeders.
Vergils Konstruktion
weist diese Muster auf:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
ZS |
83 |
73 |
111 |
63 |
90 |
86 |
70 |
110 |
67 |
77 |
830 |
|
FW |
83 |
73 |
40 |
13 |
13 |
45 |
14 |
18 |
67 |
18 |
384 |
Das ZS-Verhältnis
der beiden äußeren (1+10) Verszahlen zu den beiden inneren (5+6) beträgt 160:176 = 16*(10:11); 160+176 = 336.
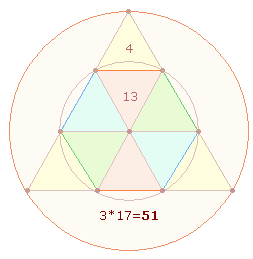
Die mittleren Verszahlen 111+110 der 3. und 8. Ekloge sind Konstitutivzahlen ihrer Summe 221 = 17*13.
|
|
2 |
3 |
4 |
|
7 |
8 |
9 |
|
|
VZ |
73 |
111 |
63 |
247 |
70 |
110 |
67 |
247 |
|
FW |
73 |
40 |
13 |
126 |
14 |
18 |
67 |
99 |
Die Summen der jeweils
benachbarten Zahlen 73+63 und 70+67 sind ebenfalls angrenzend: 136+137 = 273 = 21*13, in Parallelstellung sind sie paarweise durch 13 teilbar: 73+70
= 11*13, 63+67 = 10*13.
Das Verhältnis der zwei mittleren zu den vier umgebenden Verszahlen ist 221:273 = 13*(17:21) = 13*38 = 2*13*19. 17:21 DR-Elemente
bedeuten das Verhältnis von 3:4 Dreiecken:
|
|
Der höheren Mittelpunktszahl steht
die niedrigere Summe der Nachbarzahlen gegenüber (111+136)
und umgekehrt (110+137), so daß beide
Dreiergruppen aus jeweils 247
= 13*19 Versen bestehen. Auch die FS der beiden Hälften bilden ein Zahlenverhältnis:
126:99 = 9*(14:11).
In Bezug auf die 8 Flächen des Oktaeders beziehen sich die Zahlen 13 und 19 besonders
auf Punkte und Flächen
des Hexagons und der Tetraktys: 7+6, 10+9. 13:19 Elemente bedeuten dann das
Kreisflächenverhältnis 1:3.
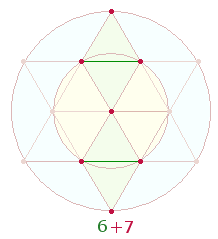
Außerdem ist 13 die FS
6+7 der Zahlen 9 und 10.
7.
Die beiden oben eingeteilten Zahlengruppen, nämlich die vier
konzentrisch äußeren und inneren Verszahlen sowie die zweimal
drei
dazwischen liegenden, bergen ein erstaunliches Geheimnis: Sie bilden genau die FS und ZS der KAPITOLINISCHEN TRIAS ab:
|
|
ZS |
FS |
|
|||||||||
|
IUPPITER IUNO MINERVA |
242 |
173 |
415 |
|||||||||
|
OPTIMUS MAXIMUS REGINA |
252 |
163 |
415 |
|||||||||
|
|
494 |
336 |
830 |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
83 |
73 |
111 |
63 |
90 |
86 |
70 |
110 |
67 |
77 |
|||
Die FS der Verszahlen 1
und 5 beträgt 83+90
= 173, die der zweiten
Begrenzungsnummern 6 und 10 86+77 = 163. Die beiden Summen
entsprechen den FS der Kapitolinischen Trias
(173) und der drei Beinamen (163). Die Summe 247+247
= 494 der 6 dazwischen liegenden Verszahlen
ist identisch mit der ZS der 6 Namen.
Statt zweimal 415 konstruiert Vergil zweimal
247.
|
Ekl. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
55 |
|
ZS |
83 |
73 |
111 |
63 |
90 |
86 |
70 |
110 |
67 |
77 |
830 |
|
FW |
83 |
73 |
40 |
13 |
13 |
45 |
14 |
18 |
67 |
18 |
384 |
1.
Die FS der 10 Verszahlen beträgt 384 = 4*96, ihr FW 4+13 = 17. Der FW der Verssumme 830 ist 90, beide FW zusammen ergeben 107. Die Zahl 17 und 107 besagen hier
dasselbe: 10+7, bezogen auf 10 Tetraktyspunkte und 7 hexagonale Punkte.
Die ZS+FS beträgt 830+384 = 1214. Die beiden 2-stelligen
Zahlen 12+14 sind Aufteilungen der 26 Oktaederelemente:
12 Kanten (Linien) sowie 6 Ecken (Punkte) +
8 Flächen.
2.
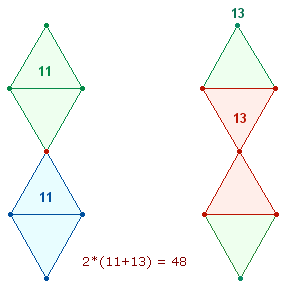
Aus
jeweils 4 Doppelrauten von je 11 Elementen oder 4
sanduhrförmigen Doppeldreiecken von je 13
Elementen oder in Kombination von 2+2 der
beiden Figuren (48 Elemente) oder in
doppelter Sichtweise (96 Elemente) läßt sich
ein Oktaeder zusammensetzen:
|
|
3.
Nimmt man die ZS 494 und FS 336 der kapitolinischen
Trias als ein Konstruktionsprinzip der 10 Verszahlen, kommt mit
der FS
384 eine
weitere Summe hinzu, mit der die FS 336 das Verhältnis 48*(7:8) bildet. Die
Verhältniszahlen sind auf den DR-Rahmen aus 7 Punkten und 8 Linien, die Teilungszahl 48 auf 2*(11+13) der vorstehenden Figuren beziehbar.
Die FW
der beiden FS 336
und 384 sind
18
und 17,
ihnen entsprechen die Buchstaben SR. Der FW
der ZS 494 = 26*19 ist 15+19 = 34. Zusammen ergibt sich daraus die ZS des Wortes SATOR:
|
S |
A |
T |
O |
R |
|
18 |
1 |
19 |
14 |
17 |
III. Die 10 Verszahlen im Kreismodell
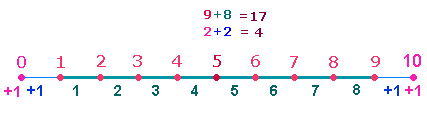
1.
Die 10 Eklogen können als Punkte einer Skala von regelmäßigen Abständen oder als Maßeinheiten dargestellt werden. Dabei wird jede
Zahl von Maßeinheiten von einem Punkt mehr begrenzt. Wenn Maßeinheiten auf
einem Kreis angeordnet werden, fällt der letzte Begrenzungspunkt mit dem ersten
zusammen. Es ist also anzunehmen, daß Vergil die Darstellung als Maßeinheiten
und Punkte miteinander in Einklang gebracht hat:
|
|
|
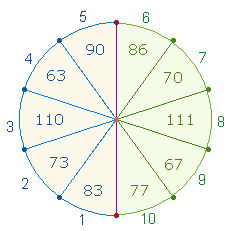
2.
Die linke Figur zeigt Parallelität
zweier Hälften. Die ersten vier parallelen Paare sind jeweils durch 13 teilbar:
|
Ekl. |
1 |
6 |
2 |
7 |
3 |
8 |
4 |
9 |
5 |
10 |
|
ZS |
83 |
86 |
73 |
70 |
111 |
110 |
63 |
67 |
90 |
77 |
|
sm/13 |
13 |
11 |
17 |
10 |
– |
|||||
|
24:27 = 3*(8:9) |
||||||||||
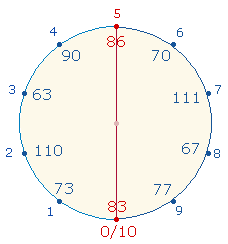
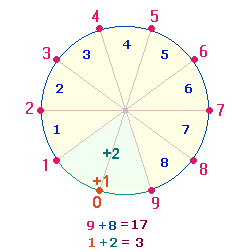
Wenn die 1.
Ekloge auf den Punkt 0 gesetzt wird, ist sie
die Vollendung der 10. Ekloge. Dadurch rücken alle
Eklogen um eine Stelle vor:
|
|
Die
Verssummen der Nummern 1 und 10 und 5 und 6 sind jeweils gleich: 73+83
= 86+70 = 156, zusammen 24*13; die
Summe der Einzelziffern ist jeweils 21. Auch in diagonaler Paarung sind die Summen durch 13 teilbar: 73+70 = 143 = 11*13, 83+86 = 169 = 13*13.
Die
Einzelziffern der Faktoren 24*13 sind auf 2:4 Linien des DR-Durchmessers
beziehbar und geben das Kreisflächenverhältnis 1:3 wieder.
Die
Verssummen 63+67
= 130 = 10*13 der Sektoren 3 und 8 bilden die horizontale Mitte des Kreises.
Die 110+111
= 221 = 17*13 in den Sektoren 2 und 7 liegen dazwischen und
bilden mit den 3 anderen Paaren das Verhältnis 17*13*(1:2).
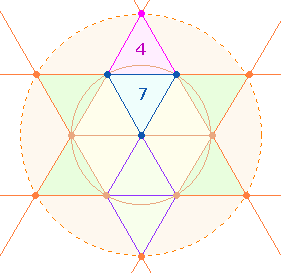
Die Zahl 17 bezieht sich auf eine
fischförmige Figur, die aus dem Ineinander von Doppeldreieck und Raute
entsteht:
|
|
Die Zahl
221 bedeutet, daß das
Doppeldreieck 2 Dreiecksflächen, die Fischfigur 2+1 enthält. 2:3 Dreiecksflächen entspricht das
Kreisflächenverhältnis 1:3.
Die
Verssumme 167 der Sektoren
4+9 ist nicht durch 13 teilbar. Dafür ist 4+9 selbst 13, sodaß die 4:1 Paare die 4 ersten Zahlen in ihren Numerierungssummen aufweisen: 42+13.
Die Verszahlen 111 und 110
können als Zahlenfolge 1-11 und 1-10 interpretiert werden und zeigen so die Thematik
von linearer und kreisförmiger Darstellung von 10
Maßeinheiten und ihren Begrenzungen auf.
3.
Die eingangs ermittelten 4 konzentrisch angeordneten Eklogen, die
jeweils 3 Eklogen einrahmen,
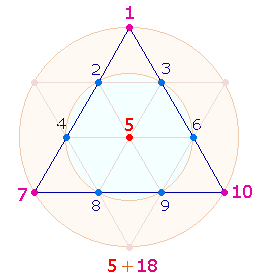
bilden auch hier eine bedeutsame Einteilung: Die ZS der übrigen 6 Eklogen beträgt 351+167 = 518 = 14*37 >46. Entsprechend den Einzelziffern des FW 46 ist die
Numerierungssumme der Eckpunkte und des Mittelpunktes der Tetraktys 5+18 = 23:
|
|
Den Zahlen 5 und 18
entsprechen den Buchstaben ES – Du bist als eine grundlegende religiöse Aussage.
Im Wort VESTA nimmt ES die Positionen 2
und 3 ein, die mit der Numerierungssumme 23 übereinstimmen. Die
Einzelziffern der Primzahl 167 bedeuten (1+6)+7 Punkte des Tetraktyssterns und geben das
trinitarische Kreisflächenverhältnis 1:3
wieder. 16 besteht aus den Summen 1-3 und 1-4 = 6+10, die beiden Endziffern ergeben 7.
4.
Bei der Addition der ZS+FS der Hälften 1-5 und 6-10 der zweiten
Kreisfigur zeigt es sich, daß beide Summen gleich sind:
|
|
ZS |
FS |
sm |
Fkt. |
FW1 |
FW2 |
sm |
|
li. Hälfte |
423 |
184 |
607 |
9*47 |
53 |
29 |
82 |
|
re. Hälfte |
407 |
200 |
607 |
11*37 |
48 |
16 |
64 |
|
|
|
|
|
|
101 |
45 |
146 |
|
184:200 = 8*(23:25); 146 = 2*73 |
|||||||
Auf eine
detaillierte Auswertung der Ergebnisse soll verzichtet werden, da die Tatsache
der Summengleichheit bereits staunenswert genug ist. Die Faktoren 2*73 können auf zwei Tetraktys (7+3 Punkte) bezogen werden.
Was ist
an der Primzahl 607 so bedeutsam, daß Vergil sie zu Summen zweier Hälften machte?
Mehrere Möglichkeiten sollen dargelegt werden:
·
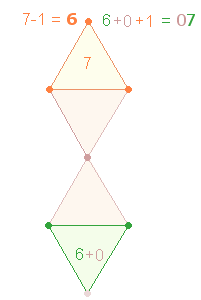
Offensichtlich geht es darum, die erste Position an die letzte
Stelle zu setzen, wie es zuvor die Kreisdarstellung gezeigt hat. Jedes Dreieck
besteht aus 7
Elementen. Durch den Schnittpunkt des hexagonalen Doppeldreiecks fallen zwei
Scheitelpunkte zusammen, sodaß die Zahl von 14 Elementen sich auf 13 reduziert.
Bei der Oktaederbildung wird die untere Raute um den Mittelpunkt gefaltet und mit der oberen deckungsgleich gemacht. Dann werden die Querlinien in einem solchen Winkel gefaltet, daß die Hälfte der unteren und der oberen Pyramide entsteht. Der untere und obere Punkt fallen zusammen und es kommt ein zweites Doppeldreieck zustande. Wenn sich nun der untere Punkt über den oberen legt, ist dessen Wert die Vollendung der Kreisbewegung. Der 7. Punkt fällt also an das nach oben gebogenene untere Dreieck:
|
|
· Die
Zahl 607 kann zweistellig aufgeteilt werden:
|
|
|
|
|
sm |
FW |
sm |
|
Zahl |
60 |
67 |
07 |
134 |
69 |
|
|
FW |
12 |
67 |
7 |
86 |
45 |
|
|
sm |
|
|
|
220 |
114 |
|
|
FW |
|
|
|
20 |
24 |
44 |
|
20:24 = 4*(5:6) |
||||||
Die Einzelziffern der ZS 134 können
als Gleichung von 1+3 = 4 Punkten der DR aufgefaßt werden:
|
|
Komplementär zu einem Mittelpunkt ist die DR auch mit zwei
Mittelpunkten versehen zu denken.
Die Einzelziffern der FS
86 weisen darauf hin, daß bei Vereinigung der
beiden äußeren Punkte ein Punkt entfällt; die 8 Rahmenlinien bleiben gleich.
Im Verhältnis 5:6 zeigt sich die Gliederung der Rautenelemente: 5 Linien und 4 Punkte + 2 Flächen. Aus 4 Rauten setzt sich ein
Oktaeder zusammen.
· Ein Oktaeder besteht einerseits aus 26 Elementen, diese
können aber nicht aus zweimal 13 zusammengesetzt werden. Gewissermaßen als Ersatz können
dafür zwei DR
eintreten mit 6 Binnenelementen und 7 Punkten:
|
|
Zweimal 6 Binnenelemente stellen im Oktaeder 8 Flächen und 4 Linien der
Mittelbasis dar.
· 60+7 verbindet die Tetraktys
mit der DR: Von jeder der 6 äußeren Ecken können 10
Tetraktyspunkte numeriert werden. Sie alle gründen auf 7
hexagonalen Punkten. Die DR besteht aus 7 Punkten und 10
Linien.
· Die
Punktestruktur der DR ist 313
mit einem und 3113
mit 2 Mittelpunkten. Die FW beider zusammengesetzter Zahlen ist 607:
|
|
|
|
sm |
FW |
|
ZS |
313 |
3113 |
3426 |
576 |
|
FW |
313 |
294 |
607 |
607 |
|
sm |
1183 = 7*13² >33 |
1183 |
||
(7+13)+13 Punkten entsprechen (1+3)+3 = 7 Flächeneinheiten.
5.
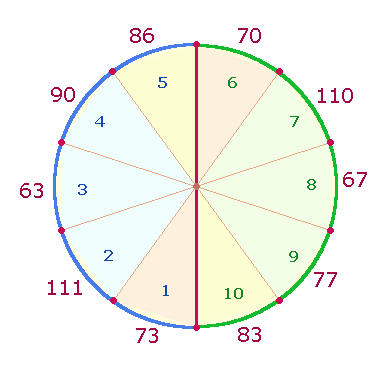
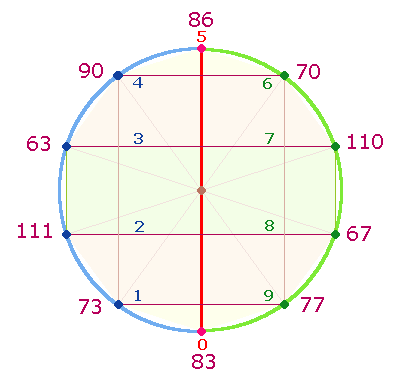
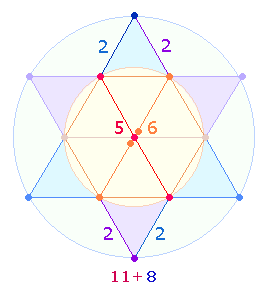
Wenn die 10 Verszahlen auf Kreispunkte gesetzt werden, ergeben sich weitere Zahlenbeziehungen:
|
|
Auf 4 horizontalen Ebenen
dieses Kreismodells ergänzen sich je zwei (blau und grün) Numerierungen zu 10. In zweistelliger Zusammensetzung ergeben das äußere und
innere Paar jeweils 65 und in der Umkehrung 155: 19+46 = 65; 28+37 = 65; 91+64 = 155; 82+73 = 155. Es kommt so das Verhältnis 130:310 = 10*(13:31) zustande.
Die Umkehrfaktoren 13 und 31 sind auch in den
horizontalen Additionsergebnissen der inneren und äußeren Paare der Verszahlen enthalten: (111+67)+(63+110) =
351 = 27*13,
73+77 = 150; 90+70 = 160; 150+160 = 310. Mit den vertikalen Zahlen 83+86
= 169 = 13*13 kommt ein weiteres durch 13 teilbares Ergebnis
zustande, sodaß sich die Gesamtzahl 830 aus 520+310 zusammensetzt.
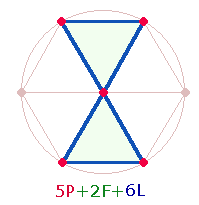
Die vier genannten
komplementären Zahlenpaare ergeben sich durch schleifenförmige Numerierung der DR-Punkte:
|
|
Im Hinblick auf die
Oktaederbildung und der Vereinigung der äußeren Punkte wird auch der obere
Punkt doppelt, also mit 5 und 0 besetzt. Zu den 7 DR-Punkten kommen also noch 2+1 Positionen hinzu. Die Zahl 607 bietet hier eine
Parallele durch die ZS der lateinischen Zahlzeichen:
|
|
D |
C |
V |
I |
I |
|
|
ZW |
4 |
3 |
20 |
9 |
9 |
45 |
|
FW |
4 |
3 |
9 |
6 |
6 |
28 |
|
|
|
|
|
|
|
73 |
45 und 28 sind die Summen der
Zahlen 1-7 und 1-9. Die Addition 1214+73 = 1287 = 9*11*13 >FW 30 stellt dieselbe
Situation von 3 Zusatzpositionen (18, 17, 16) in umgekehrter Richtung dar:
|
|
11 und 13 sind die Elemente der
beiden Figuren, durch die der Oktaeder zusammensetzbar ist. 1287+30 ergibt 1317 = 3*439 >FW 442 = 2*221 = 2*13*17. Wie oben dargelegt, hat Vergil das Produkt 3*13* auf 4
Verssummenzahlen angelegt.
1. Die Teilung der ZS+FS 1214 in zweimal 607 hat ihr Vorbild in der Kapitolinischen Trias. Dort sind es zweimal
415. Auch die ZS 830 von Vergils 10 Eklogen läßt sich in zweimal 415 aufteilen. Beide
Faktorensummen sind durch 8 teilbar:
|
|
1 |
2 |
4 |
6 |
8 |
21 |
3 |
5 |
7 |
9 |
10 |
34 |
|
ZS |
83 |
73 |
63 |
86 |
110 |
415 |
111 |
90 |
70 |
67 |
77 |
415 |
|
FW |
83 |
73 |
13 |
45 |
18 |
232 |
40 |
13 |
14 |
67 |
18 |
152 |
|
232:152
= 8*(29:19) |
||||||||||||
Die Summe der Einerzahlen ist auf
beiden Seiten 15 und auf die Rahmenelemente 6+9 und 7+1+7 der DR
beziehbar.
Die Einzelziffern der
Verhältniszahlen 29 und 19 weisen auf die Punktezahl 2+9 und 1+9 des
Strecken- und des Kreismodells auf der Grundlage der Grundzahlen 1-9 hin:
|
|
|
1. Die Einzelziffern der Zahl 415 = (4+1)+5 weisen auf zweimal 5 Radialelemente der DR hin, verdoppelt auf 15+2 Rahmenelemente der DR. Der FW von 415 ist 5*83 = 88 = 8*11. 11+8 Elemente kommen
durch den Doppelaspekt von 9 Durchmesser- und 10 Radialelementen zustande:
|
|
8+8 = 16 symmetrische Elemente + 3 Doppelpunkte geben in den Einzelziffern die 10
Punkte der Tetraktys wieder.
Die Faktoren 5 und 83 weisen auf
den theologischen Aspekt des einen Gottes in drei Personen hin. Demnach geht
die zweite Person aus der ersten hervor und die dritte
verbindet beide. Geometrischer Bezug sind zwei Rauten und ein sanduhrförmiges
Doppeldreieck im Hexagon:
|
|
Das Hexagon wird umfaßt durch die
Tetraktys, von deren drei Ecken jeweils eine Raute ausgeht:
|
|
Außer drei Rauten enthält die Tetraktys drei Doppeldreiecke
und drei Fischfiguren. Diese drei Figuren
bestehen aus 11, 13
und 17 Elementen. Somit kommt für das
Hexagon und die Tetraktys folgende Rechnung zustande:
|
|
5 Rt. |
4
Dpdr. |
3 FF. |
sm |
FW |
sm |
|
El. |
55 |
52 |
51 |
158 |
81 |
|
|
FW |
16 |
17 |
20 |
53 |
53 |
|
|
sm |
|
|
|
211 |
134 |
|
|
FW |
|
|
|
211 |
69 |
280 |
|
280 = 10*28 >FW 7+11
= 18 |
||||||
Die Summen 52+51 sind angrenzende Konstitutivzahlen ihrer Summe 103, die durch 10+3
die 13 Punkte des Tetraktyssterns wiedergibt
bzw. das Kreisflächenverhältnis 1:3. Die
Primzahl 211 ist als
Kreisflächenverhältnis (2+1):1 = 3:1 zu verstehen, die FS 134 als
1+3 = 4 DR-Punkte. Das
Kreisflächenverhältnis 1:3
bedeutet auch die FW-Aufteilung 7+11, nämlich 7
hexagonale Elemente zu (7+4) Elementen der
Raute. Darauf weisten auch die Faktoren 7*4 = 28:
|
|
Man kann die Zahl 415 als dreistellige Zahl, als dreimal zweistellige
Zahl und 3 Einzelzahlen addieren:
|
|
|
|
|
|
|
|
|
|
|
|
|
415 |
41 |
15 |
45 |
4 |
1 |
5 |
526 |
265 |
|
FW |
88 |
41 |
8 |
11 |
4 |
1 |
5 |
158 |
81 |
|
sm |
|
|
|
|
|
|
|
684 |
337 |
|
684 = 2*18*19 |
|||||||||
Wesentliches Ergebnis ist die ZS 526, deren FW 265
dieselben Einzelziffern enthält und die den Elementen des sanduhrförmigen
Doppeldreiecks entsprechen:
|
|
Auf theologischer Ebene ist die
zweite göttliche Person Abbild der ersten Person. Die beiden hexagonalen Rauten
rechts und links werden so bestätigt und ergänzt:
|
|
415 ist in den Einzelziffern dem
Modell VESTA zuzuordnen und unter der Kapitolinischen Trias behandelt.
2. Die Zahl 830 >FW 90 = 9*10 fügt der ersten Tetraktys und der ersten Doppelraute eine weitere
gleiche Figur hinzu. Die zweistellige Aufteilung 83+80+30 = 193 enthält in den
Einzelziffern die Punktestruktur des
Tetraktyssterns, 9 und 10 die Durchmesser- und Radialelemente der DR-Zickzacklinie. 9 und 10 sind Komplementärzahlen zu 1 und 2, woraus sich durch Addition 19-3 ergibt. Theologisch
werden so die drei göttlichen Personen umfaßt.
Die Konstitutivzahlen für 830 sind 414 = 18*23 >31 und 416 = 32*13
>23; 31+23 =
54; 830+54
= 884 = 4*221 = 4*13*17
>34.
3*221
wurde oben bereits als Gliederungssumme der 830
Verse ermittelt. Der Rautenaspekt der Zahl 83
verweist auf die beiden anderen Figuren in Tetraktys und DR. Der FW 34 ist
auf zwei Oktaederhälften von je 17 Elementen
beziehbar.
830 ist die 684.
zusammengesetzte Zahl nach der 146. Primzahl.
Sowohl 684 = 2*18*19 und 146 = 2*73 sind auf zwei Tetraktys beziehbar: 18+19 = 37 Elemente, 7+3
= 10 Punkte.
Erstellt: Mai 2009
Neu bearbeitet: November 2012, März 2019