Die Zahl
136
1. Im vorigen Kapitel wurden 10 Zahlen von 12-21 und 19 Zahlen von 13-31 zentriert in 5 innere und 5 äußere Zahlenpaare
angeordnet und entsprechend numeriert. In der folgenden vereinfachten Tabelle
sind die Zahlensummen (ZS) und Faktorensummen (FS) eines
Zahlenpaares bereits zusammengefaßt:
|
|
13/31 |
14/30 |
15/29 |
16/28 |
17/27 |
18/26 |
19/25 |
20/24 |
21/23 |
22 |
|
|
|
1 |
2 |
3 |
4 |
5 |
5 |
4 |
3 |
2 |
1 |
|
|
ZS |
44 |
44 |
44 |
44 |
44 |
44 |
44 |
44 |
44 |
22 |
418 |
|
FS |
44 |
19 |
37 |
19 |
26 |
23 |
29 |
18 |
33 |
13 |
261 |
|
|
88 |
63 |
81 |
63 |
70 |
67 |
73 |
62 |
77 |
35 |
679 |
|
|
|
|
|
273 = 13*21 |
|
|
|
|
|||
|
|
|
|
|
|
|
12/21 |
13/20 |
14/19 |
15/18 |
16/17 |
|
|
|
|
|
|
|
|
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
33 |
33 |
33 |
33 |
33 |
165 |
|
|
|
|
|
|
|
17 |
22 |
28 |
16 |
25 |
108 |
|
|
|
|
|
|
|
50 |
55 |
61 |
49 |
58 |
273 |
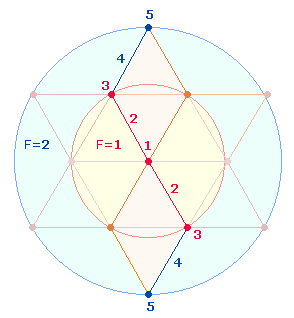
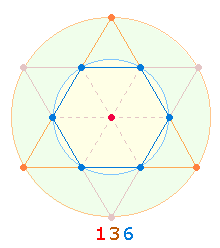
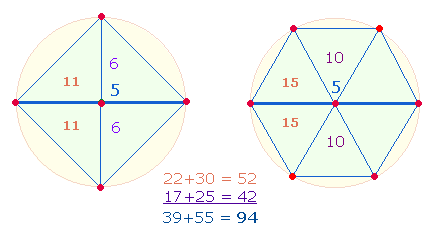
Es zeigte sich, daß die 4 ZS+FS 273 der Nummern 4554 gleich den 5 ZS+FS der Zahlen 12-21 sind. Diese Gleichheit ist im Zusammenhang mit der Erweiterung des Hexagons zum Tetraktysstern und seiner zwei konzentrischen Kreise zu sehen. Das Kreisflächenverhältnis des äußeren Kreisrings zum hexagonalen Kreis ist nämlich 2:1 und die numerierten Radialelemente der Erweiterung sind 4 und 5:
|
|
Die mittig dargestellte Doppelraute (DR) besteht aus 21 Elementen, davon gehören 13 Elemente dem hexagonalen Bereich an. Dem Verhältnis von 13:21 Elementen entspricht also die Fläche des hexagonalen Kreises zum ganzen äußeren Kreis, nämlich 1:3. Auf diese Weise wird zwischen beiden Zahlenreihen ein innerer Zusammenhang hergestellt.
2. 2+4 ZS+FS der
Zahlen der Reihen 12-21 und 13-31 unter
den Nummern 4 und 5 haben das Verhältnis 105:273 = 21*(5:13):
|
12/21 |
13/20 |
|
|
5 |
4 |
|
|
33 |
33 |
66 |
|
17 |
22 |
39 |
|
50 |
55 |
105 |
|
16/28 |
17/27 |
18/26 |
19/25 |
|
|
4 |
5 |
5 |
4 |
|
|
44 |
44 |
44 |
44 |
176 |
|
19 |
26 |
23 |
29 |
97 |
|
63 |
70 |
67 |
73 |
273 |
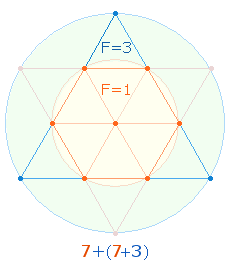
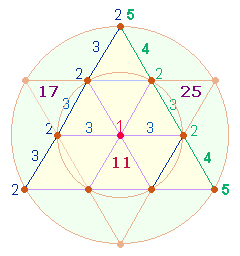
Die FS der 6 Zahlenpaare beträgt 136 = 8*17. Die FW 7+10 der Zahlen 12 und 21 als Ausgangsfaktor der Gesamtsumme beziehen sich auf 7 hexagonale und 10 Tetraktyspunkte:
|
|
Die konzentrischen Punktezahlen geben das Kreisflächenverhältnis 1:3 wieder. 2 und 3 weitere FS sind durch 17 teilbar:
|
|
ZS |
sm |
FS |
sm |
GS |
||||
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
|
|
|
|
33 |
77 |
132 |
242 |
17 |
51 |
68 |
136 |
378 |
|
FW |
14 |
18 |
18 |
50 |
17 |
20 |
21 |
58 |
108 |
|
50:58 = 2*(25:29); 108:378 = 54*(2:7); 81:405
= 81*(1:5) |
|||||||||
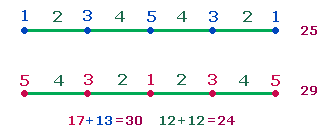
25 und 29 sind Numerierungssummen von innen und von außen von 1-5:
|
|
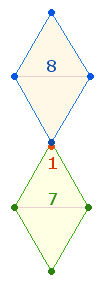
3. Die FS 70 der 3 Fünfernummern und
die FS 66 der 3 Vierernummern haben
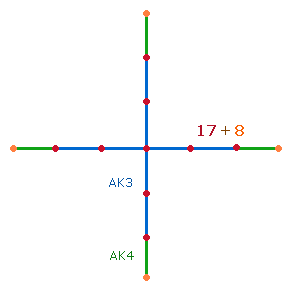
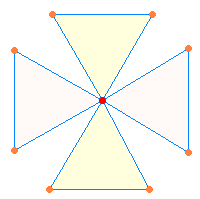
das Verhältnis 2*(33:35). Aus den Verhältniszahlen lassen sich zwei Achsenkreuze
bilden, das eine mit einem, das zweite mit zwei Mittelpunkten:
|
|
|
Die
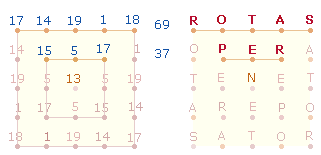
Winkelverschiebung des zweiten Achsenkreuzes bildet die Grundlage des SATOR-Quadrats, da den Zahlen 18 und 17 die Buchstaben SR entsprechen.
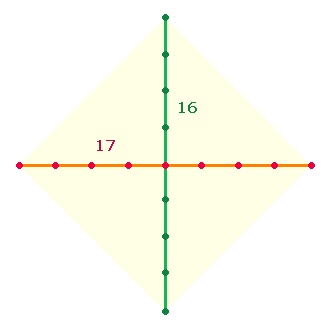
4. Die FS 136 ist ein Siebtel der Gesamt-ZS+FS 952 und Summe der Zahlen 1-16. Die Einzelziffern weisen
klar auf die Punktestruktur der Tetraktys:
|
|
Die Frage, wie die Zahlen 1-16 in Beziehung zur Tetraktys stehen, ist einerseits nicht so schwer zu beantworten, andererseits doch mit einigen komplexeren Gesichtspunkten verbunden.
Eine Quadratzahl, z.B 16, setzt sich stets aus der Summe fortlaufender Zahlen von 1 bis zu je zwei angrenzenden Zahlen zusammen, von denen die höhere die Wurzel der Endsumme ist. In vorliegendem Fall ist es die Wurzel 4 und die darunter liegende Zahl 3: Die Summe von 1-3 ist 6, von 1-4 10.
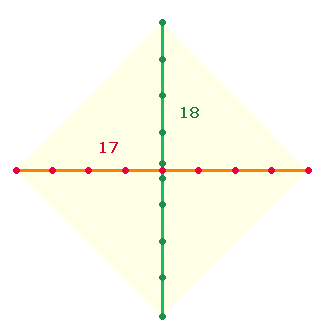
Den Zahlen 3 und 4 entsprechen die Kreisflächenverhältnisse 1:2 und 1:3. Eine Tetraktysseite besteht aus 3 Linien und 4 Punkten aber auch aus 3 hexagonalen und 4 Erweiterungselementen. Mit letzteren lassen sich Entsprechungen zu Kreisflächenverhältnissen herstellen: 3:4 Elemente bedeuten 1:2, 3:7 Elemente das Keisflächenverhältnis 1:3. Auf diese Weise geben 6+11 = 17 Elemente einer Tetraktysseite 7 Kreisflächeneinheiten wieder.
Wenn man Punkte und Linien der hexagonalen Achse numeriert, bezeichnet man den Mittelpunkt als 1, die Kreislinienpunkte als 2 und die Linien als 3. Für eine Tetraktysseite erhält man so die Summe 17. Man kann diese Numerierung für die Erweiterungselemente mit 4 und 5 fortsetzen und erhält so die Summe 25:
|
|
Die Nummern 4 und 5 spielen also die Rolle, die auch bei den beiden Zahlenreihen beobachtet wurde.
Die Erweiterung der Numerierungssumme 17 auf 25 entspricht dem addierten Produkt 17*8 für die Zahlen 1-16.
Achsenkreuze können konzentrisch erweitert werden. Das erste erweiterte besteht aus 17 Elementen, das darauf folgende aus 8 Elementen mehr:
|
|
Durch diagonale Verschiebung eines Achsenarmwinkels gegen den anderen entsteht ein Quadrat. Eine Seite dieses Quadrats besteht so wie eine Tetraktysseite aus 4 Punkten und 3 Linien.
5. 17*8 ist also als 17+8 auffaßbar und stellt
eine Erweiterung dar. Das ist auch bei den zwei grundlegenden zwei- und dreiachsigen
Achsenkreuzen und ihrer Flächenausprägungen der Fall, des Rautenquadrats und
des Hexagons:
|
|
Beide
Achsenkreuzarten wirken beim Zustandekommen des Oktaeders durch ein DR-Kreuz
zusammen. Ein Achsenkreuz aus zwei hexagonalen Doppeldreiecken besteht aus 17 Achsenelementen, 4 Querlinien
+ 4 Dreiecksflächen:
|
|
6. Die Einzelziffern von
8*17 sind auf Rahmenelemente der DR beziehbar:
Sie bestehen aus 8 Linien und 7 Punkten, zu denen ein zweiter Mittelpunkt kommen
kann, oder aus 8 Rahmenelementen der ersten Raute und 1+7 Rahmenelementen der
zweiten Raute:
|
|
7. 17 ist aus 9+8 zusammengesetzt. Die
Komplementärzahlen zu 17*8 sind demnach 1+2+2 = 5. Aus 5 Elementen bestehen
entweder die hexagonale Achse oder die Radialelemente einer Hälfte des DR-Durchmessers. Da nun der
innere und der äußere Kreis zu berücksichtigen ist, sind die entsprechenden
Radialelemente (1+2)+(1+2+2) = 8. 3:5 Radialelementen entspricht das
trinitarische Kreisflächenverhältnis 1:3. Da man für jeden DR-Durchmesser zweimal 3:5 Radialelemente anlegen
kann, eine DR aus zwei
Durchmesserlinien besteht und ein Oktaeder aus einem DR-Kreuz zusammengesetzt ist,
ergeben sich insgesamt 8*8 = 64 Radialelemente.
64*11 beträgt auch die FS der 6 Umkehrungen von 178:
|
Zahl |
178 |
187 |
718 |
781 |
871 |
3552 |
|
|
FW |
91 |
28 |
361 |
82 |
62 |
80 |
704 |
|
704 = 64*11
= 32*22 |
4256 |
||||||
Der Faktor 11 weist auf die Elemente einer einzelnen Raute hin, 32*22 auf 4*8 Radialelemente für eine DR. Es ist hier daran zu erinnern, daß die FS der beiden Zahlenreihen 12-21+13-31 = 53*11 64 beträgt. Die Einzelziffern des Faktors 53 ist auf die Radialelemente 5:3 zu beziehen.
8. Das Rätsel, wie nicht
17+8, sondern 8+17 25 ergibt, löst sich im 5x5-Punkte Quadrat, das aus zwei Quadratrahmen
besteht, wie der Tetraktysstern sich in zwei konzentrischen Kreisen befindet.
Eine äußere Seite dieses Quadrats besteht aus 5 Punkten, eine innere Seite aus 3 Punkten. Es bleiben 16 Punkte + Mittelpunkt übrig.
Das 5x5-Punkte Quadrat ist auch die Grundlage des SATOR-Quadrats, das die trinitarischen Zahlenverhältnisse des Tetraktysstern abbildet. Das läßt sich an den ZS+FS der 5:3 Buchstaben erkennen:
|
|
Es ergeben sich folgende ZS+FS:
|
|
5 Bu. |
3 Bu. |
sm |
|
ZS |
69 |
37 |
106 |
|
FS |
54 |
30 |
84 |
|
sm |
123 |
67 |
190 |
|
84:106 = 2*(42:53) |
|||
Die ZS 106 = 2*53 bestätigt das doppelte Verhältnis von 5:3 Radialelementen je DR-Zickzacklinie. In der Aufteilung 10+6 zeigt sich der innere Zusammenhang zwischen 2*(5+3) Radialelementen und der Zahl 16.
Die Einzelziffern der FS 42 entsprechen 4+2 Linien der beiden Quadratseiten, sie geben im Tetraktysstern ebenfalls das Kreisflächenverhältnis 3:1 wieder.
Von den ZS und FS lassen sich wiederum die FW ermitteln:
|
|
ZS |
FS |
sm |
FW |
FW |
sm |
GS |
|
5 Bu. |
69 |
54 |
95 |
26 |
11 |
65 |
160 |
|
3 Bu. |
37 |
30 |
74 |
37 |
10 |
40 |
114 |
|
|
106 |
84 |
190 |
63 |
21 |
84 |
274 |
|
FW |
55 |
14 |
69 |
13 |
10 |
23 |
92 |
Die 4Werte-Summe 274 = 2*137 ist zu verstehen als zweimal 5+8 = 13 Radialelemente in der Bedeutung von 3+4 = 7 Kreisflächeneinheiten. 63:21 = 21*(3:1) und 69:23 = 23*(3:1) beziehen sich auf die Elemente von Dreiecken und ihre Erweiterung zu Quadraten, indem einmal eine Seite aus 2 Punkten + 1 Linie und einmal aus 2 Linien und 3 Punkten besteht. Die Einzelziffern der gemeinsamen Teiler 21 und 23 sind Entsprechungen von 2 Kreisflächeneinheiten zu 2 Erweiterungselementen und 1 Kreisflächeneinheit zu 3 Radialelementen.
Die vierfache ZS+FS der 5+3 Buchstaben + 13+13 des Mittelpunktes ergibt 437+349 = 786 = 6*131 >FW 136. Die Primzahl 131 enthält die Kreisflächenverhältnisse 1:3 und 3:1, der FW 136 kehrt zum Ausgangsmodell von 5:3 Buchstaben je Quadratseite in den beiden konzentrischen Quadraten zurück.
Erstellt: Dezember 2018