3 Kreise und 6 Kreisachsen der Dreifaltigkeit

A. I. Einleitung

II. Grundlegendes

III. Spezielles

B. IV. 5+6 Achseneinheiten

I. Einleitung

1. Der Titel der folgenden Ausführungen mag seltsam klingen. Was hat die Dreifaltigkeit mit 6 Kreisachsen zu tun? Die Antwort ist folgende: Wenn Gott selbst Zahl ist, nämlich 1 und 3, und wenn darin der ganze Sinn des Seins umschlossen ist, wie sollte es dann nicht eine Sinnordnung aller übrigen Zahlen geben? Sinnordnung bedeutet Entfaltung der Zahlen aus ihrem trinitarischen Ursprung. Jedes Detail ist von ontologischer, d.h. seinsrelevanter Bedeutung und nach logischen Regeln in seinem geistigen Zusammenhang zu verstehen.

Das Thema ließe sich weitgehend auch ohne Bezug auf die Trinität abhandeln. Aber nur die überragende Weisheit eines personalen Gottes ist ausreichender Beweggrund, im Dezimalsystem die Vollkommenheit von Sinngefügen zu erkennen.

2. Es gelte die Prämisse, daß der Kreis das vollkommene Abbild der Dreifaltigkeit darstellt: Der Kreis als Ganzheit kann nicht existieren ohne die drei Bestandteile Mittelpunkt, Kreisbogen und Fläche.

Von diesem Ausgangsmodell erfolgt jede weitere Differenzierung. Jeder weiterer Bestandteil, im Folgenden als Element bezeichnet, ist sinnträchtiger Baustein des gesamten Zahlsystems, des Dezimalsystems.

II. Grundlegendes

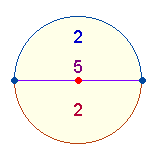
1. Im Kreisbogen ist bereits ein Maß festgelegt, das eine durch den Mittelpunkt (MP) gezogene Gerade meßbar macht. Der so erzeugte Durchmesser (DM) besteht aus zwei Radialmaßen oder Maßeinheiten, die demnach immer paarweise auftreten. Das Radialmaß des idealen Kreises sei stets 1:

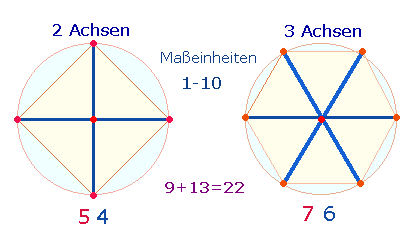
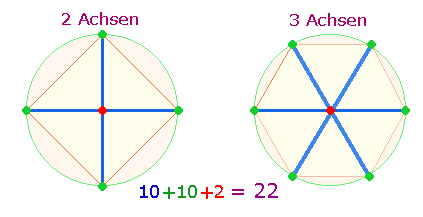
2. Es liegt nahe, die drei göttlichen Personen mit den Zahlen 1-3 gleichzusetzen. In Bezug auf die Differenzierung des Kreises sind also nach der ersten Achse Konstruktionen mit 2 und 3 Achsen zu erwarten:

Konstitutiv für das Dezimalsystem sind 10 Maßeinheiten. Diese sind in den 2+3 Achsen des rechtwinkligen Achsenkreuzes und des Hexagons verwirklicht. Erst ab zwei Achsen lassen sich rationale Verbindungslinien ziehen, die eigene Flächenfiguren, hier Dreiecke, begründen. Gewissermaßen im Nachhinein erweitert die erste Kreisachse die Norm der 10 Einheiten auf 12 als ein Ergänzungsmodell.

3. Die Zahl 3 ist Voraussetzung alles Meßbaren. Denn jede Maßeinheit bedarf zweier Begrenzungspunkte. Das führt zu der Überlegung, jeder der 10 Maßeinheiten eigene Begrenzungszahlen in fortlaufender Numerierung zu geben. Die Relevanz der Zahlen 1-30 habe ich im Zusammenhang mit dem wiederkehrenden Primzahlmuster nach 30 Zählern untersucht. Dabei ist die Einbeziehung der Faktorenwerte (FW) unverzichtbarer Bestandteil. Hier sollen bereits die Zahlensummen (ZS) und Faktorensummen (FS) einer jeden Einheit zusammen mit ihren FW aufgeführt werden:

	123	456	789	10-12	13-15	16-18	19-21	22-24	25-27	28-30
	1	2	3	4	5	6	7	8	9	10
ZS	6	15	24	33	42	51	60	69	78	87	465
FS	6	14	19	25	30	33	38	45	34	50	294
sm	12	29	43	58	72	84	98	114	112	137	759

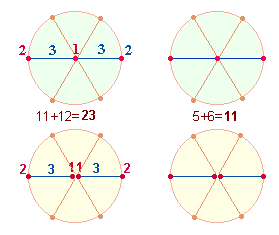
Die Gesamt-ZS+FS 759 besteht aus den Faktoren 3*11*23. Das Ergebnis zeigt zunächst den Doppelaspekt von 5 DM- und 6 Radialelementen, bzw. 11+12 in ihrer numerierten Form:

Der Faktor 3 gibt den Hexagonachsen offensichtlich Vorrang vor dem Achsenkreuz. Eine neutrale Darstellungsweise dieses Doppelaspekts zeigt der Produktausdruck 33*23, weil die Einzelziffern auf den Doppelaspekt von Radial- und Durchmesserelemente verweisen.

Schließlich berücksichtigen die Einzelziffern des Faktors 23 beide Achsenfiguren, mit Voranstellung des Achsenkreuzes.

4. Es müssen nun noch die beiden Maßeinheiten der ersten Achse hinzugefügt werden:

	31-33	34-36	sm
	11	12
ZS	96	105	201
FS	55	41	96
sm	151	146	297
297 = 27*11
759+297 = 1056

Auch die ZS+FS dieser folgenden 6 Zahlen ist durch 11 teilbar, wobei eine bemerkenswerte Umkehrung erfolgt: Denn aus 69*11 wird nun 96*11, bzw. aus 33*23 wird 33*32.

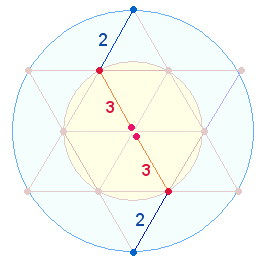
5. Die Umkehrfaktoren 23 und 32 weisen darauf hin, daß die ZS+FS der Zahlen 1-30 und 1-36 zu addieren sind. Das Ergebnis ist 33*(23+32) = 33*55 = 1815. Am ersten Ergebnis sind 5, am zweiten 5+1 Achsen beteiligt. Das entspricht wiederum dem Doppelaspekt von DM- und Radialelementen. Die Produktzahlen 33*55 entsprechen der ZS von 23+32 = 55 und ihren FW 23+10 = 33. Die Einzelziffern der Zahlen 23 und 32 sind nicht nur als Durchmesserelemente der Kreisachse zu verstehen, sondern auch als Radialelemente der beiden Tetraktyskreise:

Die Zahl 165 = 15*11 ist die FS der Zahlen 1-21. In der Aufteilung 69+96 ist sie in 3:4 konzentrischen Dreiereinheiten verwirklicht:

	1-3	10-12	19-21	sm	4-6	7-9	13-15	16-18	sm
	1	4	7		2	3	5	6
ZS	6	33	60	99	15	24	42	51	132
FS	6	25	38	69	14	19	30	33	96
sm	12	58	98	168	29	43	72	84	228
168:228 = 12*(14:19)

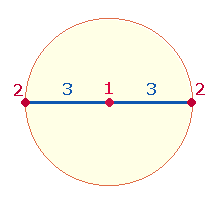
Wenn man zwischen zwei Maßeinheiten nur einen Begrenzungspunkt annimmt, ist die Zahl 21 als 10 Maßeinheiten und 11 Begrenzungspunkte zu verstehen. Dies kann in Kurzform durch 551 ausgedrückt werden. Tatsächlich ist dies z.B. die ZS+FS der Kreuzesinschrift IESUS NAZARENUS REX IUDAEORUM: 326+225.

6. Die bisherigen Zusammenhänge werden klar, wenn wir nicht von 5 Achsen, sondern von 10 Maßeinheiten ausgehen. Diese werden nämlich von 5+7 = 12 Punkten begrenzt. Davon sind zwei Mittelpunkte:

Es zeigt sich also einerseits, daß die erste Kreisachse als 2 Mittelpunkte in den beiden anderen Achsenfigur präsent ist. Andererseits weist das Produkt 27*11 der Zahlen 31-36 auf die Vollendung der 6 Achsen hin, da zu den 22 Elementen der zweiten und dritten Achse noch 5 Elemente der ersten hinzukommen. Das Verhältnis von Punkten zu Maßeinheiten ist nun 15:12 = 3*(5:4).

7. Die Zusammengehörigkeit der Zahlen 1-30 zeigt sich auch, wenn man zu den ZS und FS noch deren FW ermittelt:

	1	2	3	4	5	6	7	8	9	10
ZS	6	15	24	33	42	51	60	69	78	87	465
FS	6	14	19	25	30	33	38	45	34	50	294
FW1	5	8	9	14	12	20	12	26	18	32	156
FW2	5	9	19	10	10	14	21	11	19	12	130
156:130 = 26*(6:5) = 26*11

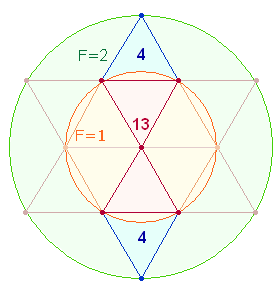
Die Summen der FW1/2 sind jeweils durch 13 teilbar, ein Hinweis auf die 13 Elemente der 3 Hexagonachsen. Die Klammerwerte des Verhältnisses 6:5 zeigen wiederum den Doppelaspekt von Radial- und DM-Elementen. Der ZS+FS 69*11 wird also 26*11 zum Endergebnis 95*11 = 1045 hinzugefügt. Dabei bildet 26 den FW von 69 (3*23). Der innere Zusammenhang der Zahlen 1-30 ist also unbestreitbar.

Die FW1/2 der letzten beiden Dreiereinheiten sind:

11	12
96	105	201
55	41	96
13	15	28
16	41	57
28+57=85		382

Die Gesamtsumme der 4Werte der Zahlen 1-36 beträgt nun 1045+382 = 1427. 1427 ist eine Primzahl. Ihre Bedeutung liegt darin, daß 14*27 = 378 die Summe der Zahlen von 1-27 ist, also der Zahl der Elemente der 6 Achsen. In der Kubikzahl von 3 sind die drei göttlichen Personen dreidimensional vereint.

8. Bisher wurde für die 2 und 3 Achsenfiguren jeweils nur ein Mittelpunkt gezählt. Gesteht man jeder Achse einen Mittelpunkt zu, ergeben sich zwei verschiedene Doppelzählungen, die in horizontalen und vertikalen Summen abzulesen sind. Maßeinheiten (ME) werden jeweils verdoppelt:

	2 Fig.			3 Fig.			GS
ME	10	12	20	12	12	24	44
Pu.	12	15	27	15	18	33	60
	22	25	47	27	30	57	104
44:60 = 4*(11:15); 104 = 8*13

8:13 DR-Elemente geben das Kreisflächenverhältnis 2:1 wieder:

Die ZS 57 und 47 treten zweimal nebeneinander im lateinischen Gloria der Meßliturgie in den Wörtern DOMINE DEUS auf. Ersteres enthält sogar das Verhältnis 30:27:

	D	O	M	sm	I	N	E	sm	GS
ZW	4	14	12	30	9	13	5	27	57
FW	4	9	7	20	6	13	5	24	44
sm				50				51	101

Nach Buchstabenzahl vertreten beide Wörter 6+4 = 10 Maßeinheiten.

9. Das Problem, daß die Kreisachse den beiden anderen Achsenfiguren nachgestellt und nicht vorangestellt ist, ist vorerst außer Acht zu lassen. Der Bezug der 12 Maßeinheiten zur Tetraktys, die aus 37 Elementen besteht und sich aus 7 hexagonalen und 3 Erweiterungspunkten zusammensetzt, geht aus zwei Umständen hervor:

Erstens, die Summe der Zahlen von 1-36 beträgt 18*37.

Zweitens, die FS und ZS der Zahlen 1-21, die 7 Maßeinheiten umschließen, sind beide durch 11 teilbar: 165:231 = 33*(5:7) = 36*12. Die ZS+FS der folgenden 9 Zahlen mit 3 Maßeinheiten beträgt 234+129 = 33*11. Beide Zahleinheiten haben demnach das Verhältnis 33*(12:11) = 33*23. Fügt man der zweiten Zahleneinheit die dritte mit 27*11 hinzu, beträgt das ZS+FS-Verhältnis von 21:15 Zahlen 11*(36:60) = 132*(3:5). Das entsprechende FS-Verhältnis ist 165:225 = 15*(11:15).

Die Ziffernfolge 1 3 2 ist in einer numerierten Kreisachse vom Mittelpunkt aus zu erkennen:

Trennt man die FW nach Punkten und Maßeinheiten, zeigen sich folgende Ergebnisse:

		1			2			3			4			5			6			7			8			9			10			11			12
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
P	1		3	4		5	7		6	7		7	13		8	8		8	19		10	13		9	10		9	11		10	31		14	19		10	242
L		2			5			6			11			9			17			9			23			15			29			10			12		148
																																					390

Die FW 10 und 12 der 11. und 12. Maßeinheit geben die 10 Maßeinheiten und 12 Begrenzungspunkten der beiden behandelten Achsenfiguren wieder.

Die FS der Maßeinheiten bilden mit deren ZS das Verhältnis 148:222 = 74*(2:3) = 370. Die ZS+FS der Punkte beträgt 444+242 = 686 = 2*7³. Die beiden Ergebnisse weisen auf zwei Tetraktys hin, auf 20 Punkte: 370 = (3+7)+10 und auf die Elemente von 2*3 Tetraktysseiten: 2*7³ = 2*(3*7). Tatsächlich lassen sich die 36 Zahlen auf den 2*18 Rahmenelementen von zwei Tetraktys anordnen. Die Punkte sind die ungeraden, die Linien die geraden Zahlen. Die ZS+FS der beiden Zahlengrupen sind 324+228 = 552 = 24*23 und 342+162 = 504 = 24*21, das ZS+FS-Verhältnis 24*(23:21).

Die 36 Zahlen lassen sich auch auf den 24 Linien und 12 Dreiecken des Tetraktysstern von oben nach unten anordnen. Dabei ist die Zahl der hexagonalen und der Erweiterungselemente jeweils gleich: Die ZS der jeweils 18 Zahlen ist 333, die FS die benachbaren Primzahlen 193 und 197, sodaß sich das ZS+FS-Verhältnis 530:526 = 2*(265:263) ergibt. Die ZW/FW-Verrechnung führt zu einem absoluten Ergebnis:

	in.	au.	sm	FW
ZS+FS	526	530	1056	24
FW	265	60	325	23
sm			1381	47
FW			PZ	PZ

Die Verrechnung kommt an ihr Ende, wenn zwei zu verrechnende Zahlen Primzahlen sind. Die Einzelziffern der Zahlen 24 und 23 geben die 6 Radial- und 5 Durchmesserelemente an, wobei Maßeinheiten und Punkte getrennt addiert sind.

Von Interesse sind die Zahlenergebnisse der oberen und unteren 6 Dreiecke:

	oben							unten
Zahl	2	8	10	12	14	16	62	21	23	25	27	29	35	160	222
FW	2	6	7	7	9	8	39	10	23	10	9	29	12	93	132
							101							253	354

Der Spiegelbildlichkeit der oberen und unteren Dreiecken entsprechen die Umkehr-FS 39 = 3*13 und 93 = 31*3.

10. Die 6 Achsen können in zwei Hälften geteilt werden: in drei Mittelachsen und die übrigen drei Achsen. Beginnt man mit der einzelnen Mittelachse und läßt die drei hexagonalen Achsen und anschließend das rechtwinklige Achsenkreuz folgen, ergeben sich folgende Werte:

	1-6			7-12			25-30
	P	L	sm	P	L	sm	P	L	sm	SM	SM	GS
ZS	14	7	21	38	19	57	110	55	162	162	81	243
FS	13	7	20	27	17	44	40	44	84	80	68	148
	27	14	41	73	36	101	150	139	245	242	149	391

	13-24 (hx)			31-36 (rw)
	P	L	sm	P	L	sm	SM	SM	GS
ZS	148	74	222	134	67	201	282	141	423
FS	88	58	146	74	22	96	162	80	242
	236	132	368	208	89	297	444	221	665

Das herausragende Ergebnis dieser Einteilung der Achsenwerte ist, daß die FS 148 und 242, die in der Gesamtberechnung getrennt auf Linien und Punkte fielen, nun in der Halbierung der Achsen für beide Bereiche in Erscheinung treten. Die ZS 243 und 423 sind Umkehrzahlen im Verhältnis 9*(27:47) = FW 12+56, deren Einzelziffern auf drei Maßeinheiten in Hexagon, Tetraktys und DR hinweisen. Die addierten FS 20+44 = 64 und 84 haben im inneren Quadratrahmen des SATOR-Quadrats eine ZS-Parallele: 64+(64+4*5).

Liest man die numerierten Radialelemente von einer Seite zur anderen, gibt es zwei Ziffernfolgen: 231 und 132. Die soeben angestellte Aufteilung entspricht der zweiten Ziffernfolge und hätte vielleicht an zweiter Stelle stehen sollen. Jedenfalls wird man bei der erstgenannten Ziffernfolge vom oberen Ende 36 ausgehen:

	36-31			24-19			6-1
	P	L	sm	P	L	sm	P	L	sm	SM	SM	GS
ZS	134	67	201	86	43	129	14	7	21	234	117	351
FS	74	22	96	51	32	83	13	7	20	138	61	199
	208	89	297	137	75	212	27	14	41	372	178	550

	30-25 (rw)			18-7 (hx)
	P	L	sm	P	L	sm	SM	SM	GS
ZS	110	55	162	100	50	150	210	105	315
FS	40	44	84	64	43	107	104	87	191
	150	139	245	164	93	257	314	192	506

Bei dieser Ziffernfolge 231 ergibt sich ein Verhältnis der Gesamt-ZS+FS 550:506 = 22*(25:23) = 22*48 = FW 13+11. Die ZS 351 und 315 sind ebenfalls Umkehrzahlen mit dem Verhältnis 9*(39:35) = FW 12+28. Die FS 28 ist die Hälfte von 56 des oberen Verhältnisses.

Die ZS der zweimal drei Mittelachsen bilden das Verhältnis 243:351 = 27*(9:13). Den Verhältniszahlen 9 und 13 entsprechen die Elemente der beiden Achsenfiguren des rechtwinkligen und des hexagonalen Achsenkreuzes.

Das ZS-Verhältnis der 6 Mittelachsen und der 6 übrigen Achsen beträgt 594:738 = 18*(33:41). Die Einzelziffern der Verhältniszahlen geben 6 Radialelemente und 5 Durchmesserelemente der Kreisachse wieder.

11. Jeweils zwei Maßeinheiten bilden eine Achseneinheit (AE). Von Interesse sind besonders die FS:

AE	1	2	3	4	5		6
	1-6	7-12	13-18	19-24	25-30		31-36
	2 5	8 11	14 17	20 23	26 29		32 35
L	7	17	26	32	44	126	22	148
	24			32		56
			26		44	70

Die FS 24 und 26 sind konstitutiv für die Zahl 50. Die ersten drei Einheiten sind also am ehesten der hexagonalen Achsenfigur zuzuordnen. Die ZS der drei Einheiten ist 57. 57 und 50 sind die ZS und FS von PATER.

Die ersten beiden und die vierte Einheit bilden mit der dritten und fünften das Zahlenverhältnis 56:70 = 14*(4:5).

Die FS von 4 Maßeinheiten betragen die Hälfte von 148: 23+29+22 = 74. Es ergibt sich also das Verhältnis von 4:8 = 4*(1:2) Maßeinheiten und 74*(1:1) FS. 12 und 11 sind vornehmlich die Zahlen für die zweite göttliche Person, da sie, im Wesen gleich, aus der ersten Person heraus gesetzt ist (1+1), der Person nach aber verschieden ist (1+2): Der Gottmensch IESUS CHRISTUS ist das Maß der ganzen Schöpfung.

Tatsächlich gibt es auffällige gematrische Parallelen zwischen den FW der ersten 30 Zahlen und den beiden Namen:

· Der Vokativ und Genitiv von IESUS ist IESU:

	ES	IU			IE	SU
ZS	23	29	52	FS	11	17	28

Die Buchstaben können so paarweise gruppiert werden, daß die vier zweistelligen Primzahlen der Maßeinheiten aufsteigend die FS und ZS von IESU ermöglichen.

· Die ZS 112 des Namens CHRISTUS ist gleich der Summe der 6 zweistelligen Primzahlen 11+13+17+19 = 60; 23+29 = 52:

	CH	R	T	SS	IU
ZW	11	17	19	13+23	29	112
FW	9	17	19	16	15	76
	20	34	38	52	44	188
	92			96
92:96 = 4*(23:24) = 4*47

Die Einzelziffern der Konstitutivzahlen 23 und 24 geben die 5 Durchmesser- und 6 Radialelemente der Kreisachse wieder.

12. Die 6 Achseneinheiten ergeben folgende FS der Punkte und Linien:

E	1	2	4		3	5		6
	1-6	7-12	19-24		13-18	25-30		31-36
	2 5	8 11	20 23		14 17	26 29		32 35
P	13	27	51	91	37	40	77	74	242
L	7	17	32	56	26	44	70	22	148
	20	44	83	147	63	84	147	96	390

Die FS von 3:2 Achseneinheiten betragen jeweils 147 = 7*21. Auch alle vier Einzelsummen sind durch 7 teilbar. Die Summen 63 und 84 vertreten die Figuren des Dreiecks und Quadrats, ihr Verhältnis ist 21*(3:4).

Fügt man von der 6. Achseneinheit der ersten FS 147 22 und der zweiten FS 147 74 hinzu, erhält man für beide Summen ein durch 13 teilbares Ergebnis: 169:221 = 13*(13:17). Es wird erkennbar, daß die 6. Achseneinheit die Erweiterung des Hexagons aus 7 Punkten zum Hexagramm aus 13 Punkten darstellt. Aus 17 Elementen besteht die "Fischfigur", die eine Fortsetzung des hexagonalen Doppeldreiecks bildet.

Die FW der 4+2 Einzelsummen führen wiederum zu Teilbarkeit durch 13:

			sm			sm				sm
FS	91	56		77	70			74	22	96
FW	20	13	33	18	14	32	65	39	13	52
65:52 = 13*(5:4) = 117; 39:13 = 13*(3:1); 96+52 = 148

Das Verhältnis der FW-Summe zur Gesamt-FS beträgt 117:390 = 39*(3:10) = 39*13 = 507.

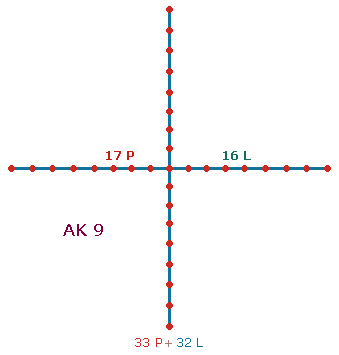
Die Einzelsummen 33 und 32 sind Elemente des Achsenkreuzes AK9:

Erstellt: Dezember 2010

Erweitert: April 2016

Start

Inhalt