ZAHL UND MASS

DIE ZWEI KOMPLEMENTÄREN KREISMODELLE DES DEZIMALSYSTEMS

I. Einleitung

II. Voraussetzungen

III. Die Kreismodelle

IV. Die Zahlen 50 und 105

V. Zahlenverhältnisse der 20 komplementären Zahlen

a) in ungerader und gerader Abfolge

b) Anordnung auf Quadratrahmen

c) Verrechnung der Gesamtsummen beider Modelle

I. Einleitung

Die beiden darzustellenden Kreismodelle dienten Vergil für die Festlegung der Verszahlen seiner 10 Eklogen und sind von mir bereits ausführlich behandelt worden. Hier soll das Wesentliche zusammengefaßt und um einige Aspekte ergänzt werden.

Die erzielten Ergebnisse sollen teils erklärt, teils dokumentiert werden.

II. Voraussetzungen

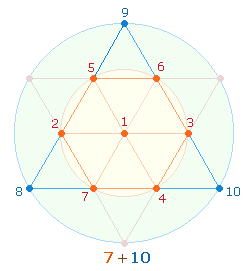
1. Es gibt 10 Grundzahlen, die nichtzählbare Null (0) und die zählbaren 1-9. Von den zählbaren Grundzahlen ist die Zahl 5 der symmetrische Mittelpunkt. Die übrigen 8 Zahlen bilden 4 symmetrische Paare, die die komplementäre Summe 10 ergeben: 1+9, 2+8, 3+7, 4+6. Die komplementäre Entsprechung 5-0 bzw. 5-10 soll als 5. Paar oder Stufe bezeichnet werden.

Symmetrische Zahlenentsprechungen sind als gleichwertig und zusammengehörig anzusehen: Die Zahl 9 z.B. ist die Entsprechung zur Zahl 1. Sie verbinden sich zu zweistelligen Zahlen, die zwei Umkehrformen bilden, z.B. 19 und 91.

2. Die Zahl 0 ist erforderlich, um den Beginn des ersten Maßes anzuzeigen, das durch den Begrenzungspunkt 1 abgeschlossen wird.

Ordnet man die Grundzahlen 0-9 als Punkte einer Kreislinie an, begrenzen sie 10 Maße. 10 Maße bilden also eine zusammenfassende Einheit, die bei Null beginnt und zur Null zurückkehrt. Die Null ist also Platzhalter von zyklisch fortschreitenden Einheiten von je 10 Maßen. Die Null selbst steht außerhalb der Dimension von Raum und Zeit, da sie kein Maß anzeigt. Das erste Kreismodell besteht also aus (Begrenzungs-) Punkten (KM-P), das zweite aus Maßeinheiten (KM-M).

Die Null ist Ausgangspunkt aller Maße und Quelle zyklischer Erweiterungen. Die Zählung der Punkte beginnt mit der 0, die der Maßeinheiten mit der 1. Dies ergibt für beide Hälften folgende Spannen:

	1.H.	2.H.
Punkte	0-4	5-9
Maße	1-5	6-10

Die beiden Zahlenreihen sind demnach versetzt anzuordnen:

Punkte	0	1	2	3	4	5	6	7	8	9
Maße	1	2	3	4	5	6	7	8	9	10

Der Unterschied der beiden Kreismodelle besteht somit in den Komponenten 0 und 10. Mit deren jeweiligen komplementären Entsprechung 5 bilden sie eine eigenständige Größe gegenüber den 4 symmetrischen Zahlenpaaren.

Dazu weitere Details

3. Das Dezimalsystem ist keine menschliche Festlegung, sondern eine absolute Seinsordnung und Sinnordnung. In prinzipieller Verallgemeinerung könnte man die Umkehraussagen formulieren: Zahl ist Sinn und Sinn ist Zahl.

Daher führen systemgerechte Modelle zu sinnvollen Berechnungen und Ergebnissen. Jede der zahlreichen Berechnungsweisen besitzt gültigen Aussagewert.

Die Ziffer Null ist also keine Erfindung, sondern Entdeckung einer objektiven Gegebenheit.

4. Zur ontologischen Seinsordnung der Zahlen gehört die Einbeziehung der Faktorenwerte (FW). Erst die Verbindung von Zahlensummen (ZS) und Faktorensummen (FS) führen zu bedeutsamen Verhältnissen und Proportionen.

Zu 0 und 10:

Der FW der Zahl 10 ist 2*5 = 7. Der FW ist integraler Bestandteil einer Zahl und ihr hinzuzufügen. Jede volle 10-er Zahl trägt das Siegel der Faktoren 5+2.

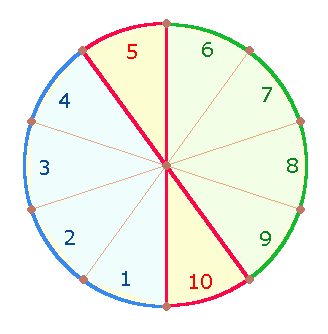
Die Null wird zählbar, wenn eine Zahl davor steht. Sie ist dann ein Multiplikationsfaktor und bedeutet das Zehnfache des vorangestellten Zahlenwertes. Diese Sonderrolle der 10 hat ihren geometrischen Bezugsort in den 10 Punkten der Tetraktys und den 7 Punkten ihrer konstruktiven Grundlage, des Hexagons:

III. Die Kreismodelle

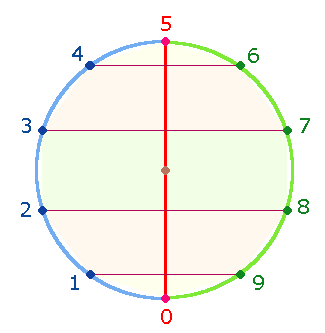
1. Das linke Modell betont die komplementäre Symmetrie der Zahlen 1-4 mit 9-6, das rechte ist geprägt von zwei Hälften von je 5 Einheiten, die in gegenüberliegende Kreissektoren unterteilt sind. Die erste Einheit der ersten Hälfte korrespondiert also mit der ersten Einheit der zweiten Hälfte (1-6 usw.)

Diese prinzipielle Unterschiedenheit der beiden Grundmodelle schließt nicht aus, daß auch den Zahlen 1-10 konzentrische Komplementarität eignet, wie ja auch die Zahlen des linken Modells in zwei 5-er Einheiten aufgeteilt werden können, jedoch mit 0 beginnend. Ebenso gibt es für die Zahlen 1-4 und 6-9 Binnensymmetrien: 1-4, 2-3, 6-9, 7-8 und die entsprechenden Umkehrungen.

Schließlich bilden auch je zwei benachbarte Zahlen in umlaufender Zahlenfolge zusätzliche Kreismodelle. Das eine beginnt dann mit 01 und endet mit 90, das andere mit 12 und 910. Hinzu kommen die entsprechenden Umkehrungen.

Eine Synopse der verschiedenen Varianten würde sich ziemlich komplex gestalten. Eine "kleine" Synopse (weil ohne 5. Stufe) von vier Modellen soll am Ende der Untersuchung dokumentiert werden.

2. Die jeweils 4 komplementären Zahlenpaare (ZP) sind in zwei äußere und zwei innere Paare mit jeweils gleicher Summe aufteilbar.Diese beträgt 5*13 = 65 (z.B. 19+46) in aufsteigender und 5*31 = 155 (z.B. 91+64) in absteigender Richtung. Der Grund dafür liegt im Summenverhältnis der komplementären Ziffern auf der unteren und der oberen symmetrischen Seite: 1+4 = 5, 9+6 = 15; 2+3 = 5, 8+7 = 15. Das Verhältnis ist jeweils 5*(1:3).

Das Zahlenpaar 05 des Punktekreises durchschneidet vertikal die 4 symmetrischen Zahlenpaare. Es entstehen so von unten nach oben 6 Punkte-Ebenen, die durch die Zahlen 1-4-1 bzw. 1-8-1 wiedergegeben werden können.

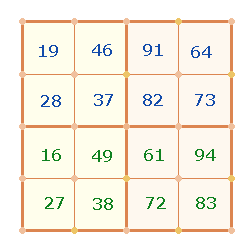
Die 16 zusammengesetzten Zahlen lassen sich in Felder eines 4*4 Quadrats einfügen:

Die Summen der aufsteigenden und absteigenden Zahlen betragen also 260+620 = 880.

3. Den zweimal vier Zahlenpaaren sind die Werte der 5. Stufe hinzuzufügen:

Stufe	5			1-4
	P	M	sm	P+M	GS
aufsteig.	05	510	515	260	775
absteig.	50	105	155	620	775
775 = 25*31

Die Werte des 5. komplementären Paares gleichen die Differenz der auf- und absteigenden Summen aus. Die Gleichheit kommt durch folgende Additionen zustande:

	1-4	5	sm
aufst.	5*52	5*103	5*155
abst.	20*31	5*31	25*31

4. Die Faktorensummen (FS) der symmetrischen Stufen 1-4 beider Kreismodelle sind der bereits erstellten Tabelle entnommen:

	ZS	FS	sm
P-Kreis	440	240	680
M-Kreis	440	257	697
	880	497	1377

Das Verhältnis der beiden Gesamtsummen 680:697 ist 17*(40:41).

Die Zahl 41 ist zu verstehen als Summe von 5*5 Punkten und 4*4 Quadratfeldern eines Quadrats, dessen 25 Punkte durch 40 Linien miteinander verbunden werden.

Die Faktoren der einzelnen Summen sind:

880	80*11
497	7*71
1377	81*17

5. Eine weiteres bedeutsames Zahlenverhältnis von ZS+FS kommt zustande, wenn man die äußeren und inneren Zahlenpaare zusammengruppiert:

	innere ZP			äußere ZP
ZS	130	310	440	130	310	440
FS	78	211	289	66	142	208
			729			648
729:648: = 81*(9:8)

Die Verhältniszahlen 9:8 lassen sich auf das Achsenkreuz des vorstehenden Quadrats beziehen: es besteht aus 9 Punkten und 8 Linien.

6. Die mit der Zahl 5 verbundenen Werte sind:

	aufsteig.			absteig.
	P	M	sm	P	M	sm	GS
Z	05	510	515	50	105	155	670
FW	5	27	32	12	15	27	59
			547			182	729
729= 27² = 9*81

Es zeigt sich, daß die 2 Zahlenpaare der 5. Stufe dieselbe ZS+FS haben wie die 4 inneren Zahlenpaare (2. und 3. Stufe). Das vollständige Zahlenverhältnis ist nun

81*(9:8:9) = 81*26 = 162*13 = 2106.

Die ZS der aufsteigenden und absteigenden Paarungen weisen dieselbe Umkehrgestalt auf wie die symmetrischen Paarungen:515 = 5*103; 155 = 5*31.

7. Die ZS+FS, die sich aus den zusammengesetzten Zahlen beider Kreismodelle ergeben, sind:

	KM-P			KM-M
Stufe	1-4	5	sm	1-4	5	sm	GS
ZS	440	55	495	440	615	1055	1550
FS	240	17	257	257	42	299	556
	680	72	752	697		1354	2106

Die ZS+FS der 5. Stufe lassen die Ausgangsfaktoren 13 und 31 der ZS der Zahlenpaare 1-4 wieder in Erscheinung treten: Die ZS 1550 ist durch 31 teilbar, die Gesamtsumme 2106 durch 13.

8. Die ZS+FS aller 5 Stufen in aufsteigender und absteigender Aufteilung sind:

	aufsteigend			absteigend
Stufe	1-4	5	sm	1-4	5	sm	GS
ZS	260	515	775	620	155	775	1550
FS	144	32	176	353	27	380	556
	404	547	951	973	182	1155	2106

IV. Die Zahlen 50 und 105

1. Die absteigenden Zahlenpaare der 5. Stufe sind 50 (KM-P) und 105 (KM-M). Sie verlaufen in Gegenrichtung, 5-0 von oben nach unten, 10-5 von unten nach oben. Absteigende Umkehrungen vollenden einen Kreis. Daher sind diese beiden Zahlen von besonderer Bedeutung. Ihre Summe 155 bildet das letzte Zehntel der Gesamt-ZS 1550.

Das Verhältnis 5*(10:21) weist auf die Zahl 21 und deren FW 10 hin.

2. Die ZS der beiden Zahlen 155 = 5*31 und ihre ZS+FS 182 = 14*13 setzen den Schlußstein der beiden Kreismodelle. Denn sie spiegeln die Summen der übrigen Zahlen wider: Teilbarkeit der ZS durch 31 und der ZS+FS durch 13.

Die ZS+FS der übrigen Zahlen (s. letzte Tabelle) ist 915+973 = 1924 = 4*37*13 = 41+13 = FW 54. Der FW der Gesamt-ZS+FS 2106 = 9*18*13 = 14+13 = 27. Somit konstrastieren die FW beider Summen durch die Umkehrungen 41 und 14. Die Zahl 14 zeigt einen neuen Umlauf an. Das FW-Verhältnis 54:27 = 2:1 bezeichnet ebenso eine Rückkehr zum numerierten Ausgangspunkt 1 zweier Kreisbogenhälften:

3. Eine weitere Gemeinsamkeit der ZS+FS 182 = 14*13 der beiden Zahlen 50 und 105 mit der Gesamt-ZS+FS 2106 = 162*13 ist die Zahl 27. Beide ZS+FS sind durch 13 teilbar, bei ersterer ergibt die Addition der Produktzahlen 27, bei letzterer ist hat die Produktzahl 162 den FW 14.

Die Zahl 182 hat durch das SATOR-Quadrat prinzipielle Bedeutung. Die ZS der zentralen Aussage SATOR OPERA TENET – Der Schöpfer erhält seine Werke ist 182, ebenso die ZS+FS der 8 verschiedenen Buchstaben PENSATOR.

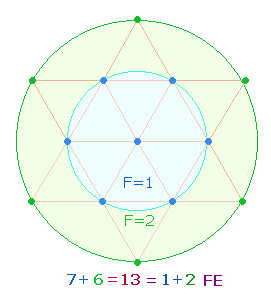
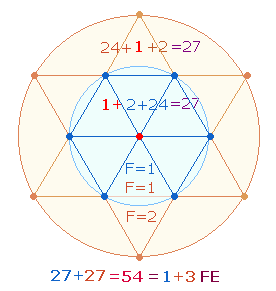
Die Zahlen 13 und 14 beziehen sich auf die Punkte des Tetraktyssterns mit seinen beiden konzentrischen Kreisen, deren Flächen sich wie 1:3 verhalten. Die Zahl 13 ist aufgeteilt zu denken in 7 Punkte des Hexagons und 6 Punkte der Erweiterung, die Zahl 14 in 7+7, wobei dem äußeren Kreis ein eigener Mittelpunkt zugestanden wird. Die Zahl 27 gibt so 3+4 Flächeneinheiten (FE) wieder:

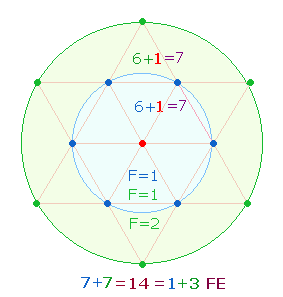
Die doppelte Zahl 54, geteilt in 27+27, läßt sich ebenfalls auf den Tetraktysstern beziehen, wenn zu den jeweils 25 Elementen eines jeden Kreises (einschließlich je 1 Mittelpunkt) der Kreisbogen und die Kreisfläche hinzugefügt werden, wobei der Hexagonkreis den Anfang und der Erweiterungskreis das Ende darstellt, weswegen die Zahl 2 einmal am Anfang (2+25) und einmal am Schluß (25+2) steht:

4. Die Zahl 50 bereitet, mit ihrem FW 12 zur Summe 62 vereint, den Schlußstein der Zahl 105 und ihres FW 15 für die Summe der absteigenden Zahlen vor: 973+62 = 1035 = 69*15. Die Werte 105+15 = 120 fügen noch weitere 8*15 hinzu. Damit wird zunächst die komplementäre Summe 15 (z.B. 6+9) für die obere symmetrische Hälfte der Grundzahlen bestätigt. Die Gesamt-ZS+FS 1155 = 11*105 aber zeigt die besondere Ausrichtung des Dezimalsystems auf die Zahlen 10 und 5.

V. Zahlenverhältnisse der 20 komplementären Zahlen

a) in ungerader und gerader Abfolge

1. Bisher wurden Zahlenverhältnisse getrennt nach den Stufen 1-4 (16 Zahlen) und der 5. Stufe (4 Zahlen) gefunden. Die 5. Stufe soll nun integriert werden. Wiederum geht es hauptsächlich um die Vereinigung von Zahlen- und Faktorensummen.

Eine Form der Gliederung ist die nach ungerader und gerader Zahlenfolge. Auf die aufsteigenden Zahlen mit der größten Zahl 510 entfallen demnach drei ungerade Positionen, auf die absteigenden zwei, was einer zu hohen Summendifferenz entgegenwirkt:

	1		3		5		7		9
	Z	FW										ZS	FS	GS
KM-P	05	5	28	11	46	25	91	20	73	73		243	134	377
KM-M	16	8	38	21	510	27	72	12	94	49		730	117	847
												973	251	1224
		2		4		6		8		10
KM-P		19	19	37	37	50	12	82	43	64	12	252	123	375
KM-M		27	9	49	14	61	61	83	83	105	15	325	182	507
												577	305	882

Das Verhältnis der beiden Gesamtsummen 1224:882 ist 18*(68:49). Auch die Endsummen bilden Zahlenverhältnisse:

377:507 = 13*(29:39) = 13*68 = 884;

847+375 = 1222 = 13*94; 884:1222 = 26*(34:47).

2. Ein weiteres Zahlenverhältnis aus vorstehender Tabelle ergibt sich, wenn man von den ZS und FS der ungeraden und geraden Folge die FW ermittelt:

	973	251	577	305	2106
FW	146	251	577	66	1040
1040:2106 = 26*(40:81)

Das interne Differenzverhältnis 40:41 verweist wiederum auf das 5*5-Punkte Quadrat mit seinen 40 Linien und 25 Punkten + 16 Quadraten.

b) Anordnung auf Quadratrahmen

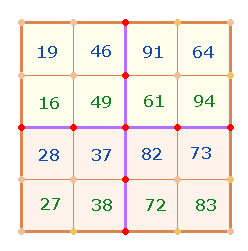
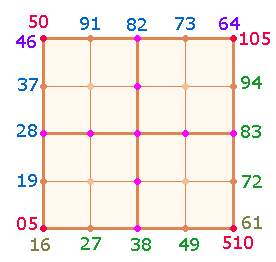
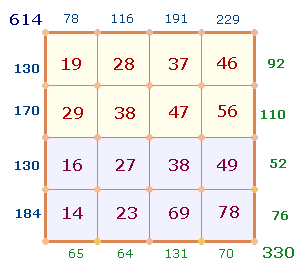
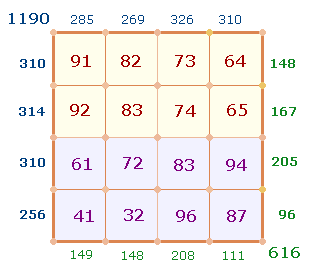
1. Die 20 Zahlen lassen sich auf dem Rahmen eines 5*5-Punkte Quadrats anordnen:

Der Beginn soll unten links liegen: Die Zahlen des Punktekreises verlaufen von unten nach oben, die Umkehrungen von oben links nach rechts, die Zahlen des Maßekreises von unten links nach rechts, die Umkehrungen von unten rechts nach oben.

Die Eckpunkte sind jeweils doppelt besetzt. Je Seite ergibt sich das Verhältnis von 2+2 Eckpunkten (EP) zu 3 Binnenpunkten (BP). Die ZS+FS der beiden Zahlengruppen sind (bei einfacher Rechnung der Eckpunkte):

	EP			BP
	ZS	FS	sm	ZS	FS	sm	GS
	857	165	1022	693	391	1084
FW	857	19	876	24	40	64	940
			1898			1148	3046
876:64 = 4*(219:16) = 4*235
876:1022 = 2*73*(6:7)

Die FS 876+64 = 940 = 20*47 bedeutet einen Durchschnittswert von 47 je Zahl. Die Teilbarkeit der Einzelsummen durch 4 teilt jeder Seite 5*47 zu. Die FW beider Summen sind 80+12 = 92 = 4*23. und bestätigen so das ermittelte Verhältnis 4*(2:3). Die zusammengesetzte Zahl 423 ist 9*47.

Die Zahl 47 erscheint auch darin sinnvoll, daß auf jeder der 4 Seiten 7 Zahlen (2+3+2) angeordnet sind.

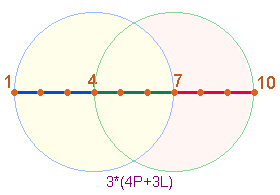
Wenn man auf einer Strecke 10 Punkte in gleichem Abstand einträgt, wird sie durch den 4. und der 7. Punkt so aufgeteilt, daß dreimal je 4 Punkte 3 Maßeinheiten begrenzen:

Beide Zahlen sind zueinander und zum Anfangs- bzw. Endpunkt gleich weit entfernt, was durch zwei Kreisumfänge deutlich wird. Jeder Kreis umfaßt 7 Punkte und 6 Maßeinheiten, zusammen 26 Elemente. Durch Hinzufügung von 3*7 Elementen gelangt man zur Zahl 47.

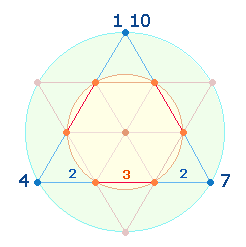
Es ist leicht zu erkennen, daß die Streckenabschnitte links und rechts der beiden Zahlen zu einem gleichseitigen Dreieck nach oben verbunden werden können und man damit die Figur der Tetraktys erhält:

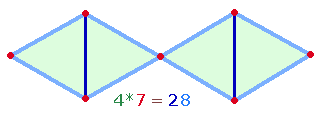
Die Zahl 21 stellt die Vollendung der dezimalen Strecke dar, da 11 Punkte erforderlich sind, um 10 Maßeinheiten zu begrenzen. Die Doppelraute im Tetraktysstern gibt dies durch 7 Punkte + 4 Dreiecksflächen und 8+2 Linien wieder. Die 4 Zahlen erscheinen in der Multiplikation 4*7 = 28:

2. Die ZS+FS der 12 Binnenzahlen ist 1084 = 4*271. Die Primzahl 271 ist zu lesen als 27+1 = 28, die Summe der Zahlen 1-7. Wenn man die 7 Punkte eines Hexagon numeriert, erhält der Mittelpunkt die Zahl 1, die Summe der 6 Kreislinienpunkte ist 27. Die Einzelziffern von 271 mit der Summe 10 lassen erkennen, daß einerseits die Tetraktys aus dem Hexagon entsteht, andererseits, daß das Hexagon dynamisch auf diese zustrebt.

Der Faktor 4 weist jeder der 4 Quadratseiten wiederum die Zahlen 4*7 zu.

3. Der organische Zusammenhang der 12 Binnenzahlen wird erkennbar, wenn man die ZS+FS der jeweils gegenüberstehenden Seiten ermittelt. Jeweils eine aufsteigende Reihe entspricht einer absteigenden:

	ZS	FS		FW1	FW2
vert.	333	211	544	43	211
horiz.	360	180	540	17	15
	693	391	1084	60	226	286
544:540 = 4*(136:135)

Die angrenzenden Verhältniszahlen 136 und 135 sind konstitutiv für ihre Summe 271. Ihre FW sind 23+14 = 37. Die Summe 271+37 = 308 = 11*28 bestätigt den Zusammenhang der Zahl 271 mit 28 = 4*7.

4. Die 4*2 Eckzahlen sind einander ebenfalls nach dem Prinzip von aufsteigend und absteigend zuzuordnen: diagonal unten links + rechts oben und rechts unten + links oben:

	ZS	FS		FW1	FW2
li.u./re.o.	190	40	230	26	11
re.u./li.o.	667	125	792	52	15
	857	165	1022	78	26	104
78:26 = 26*(2:1)

Die FW1 und FW2 der beiden Tabellen 286 und 104 sind durch 13 teilbar und haben das Verhältnis 26*(11:4) = 30*13 = 390. In anderer Gruppierung sind sie durch 6 teilbar: 138:252 = 6*(23:42).

Jeweils Binnenpunktsumme und eine Eckpunktsumme sind durch 18 teilbar:

544+230 = 774, 540+792 = 1332; 774:1332 = 18*(34:74).

c) Verrechnung der Gesamtsummen beider Modelle

1. Die ZS+FS des Punktemodells ist 752, des Maßemodells 1354. Ihre Verrechnung führt zu folgenden Ergebnissen:

			sm	FW	sm	FW
ZS+FS	752	1354	2106	27
FW	55	679	734	369
sm			2840	396	3236	813
FW			82	21	103	103
sm						916
	916 = 4*229

2. Das dritte Ergebnis 916 weist auf zwei konzentrische Quadrate aus 9+16 = 25 Punkte hin. Die Primzahl 229 kann sich auf die 4 Einzelquadrate beziehen, die durch 3*3 Punkte begrenzt werden. Das Produkt 4*229 läßt sich darstellen als 4*(2+2) + 9 = 25. Mit 4*(2+2) können sowohl 16 Punkte als auch 16 Einzelquadrate der beiden konzentrischen Quadrate gemeint sein.

VI. Eine kleine Synopse

1. Die "kleine Synopse" betrifft die Zahlen 1-4 und 6-9 von 4 Modellen, somit 16 aufsteigende und 16 absteigende Zahlen. Sie sind in zwei Grafiken dokumentiert:

Die oberen beiden Reihen zeigen die komplementär-symmetrischen Zahlen des Punkte- und Maßemodells, die 3. Reihe die parallele Entsprechungen von zwei Hälften, die 4. Reihe die Binnensymmetrien beider Hälften.

Die blauen Zahlen am Rand sind die Zahlensummen (ZS), die grünen die Faktorensummen (FS), horizontal und vertikal errechnet.

2. Charakteristisch für zweistellige Zahlen und ihre Umkehrungen ist, daß ihre Summen durch 11 teilbar sind. Die 32 Zahlen der 4 Modelle erscheinen deshalb als zusammengehörig, weil nicht nur die Gesamt-FS ebenfalls durch 11 teilbar ist, sondern auch die Summe der aufsteigenden und der absteigenden Faktorenwerte:

	aufst.	abst.	sm	Fkt.
ZS	614	1190	1804	164*11
FS	330	616	946	86*11
	944	1806	2750	250*11
330:616 = 22*(15:28)

Die ZS+FS der oberen und unteren zwei Reihen (R) sind jeweils durch 11 teilbar:

R	ZS	FS	R	ZS	FS
1	440	240	3	440	257
2	484	277	4	440	172
	924	517		880	429
	84*11	47*11		80*11	39*11
	131*11			119*11

Die Zahl 250 = (2*5)*(5*5) weist in doppelter Weise auf das Dezimalsystem hin und in den FW 7+10 auf die Punktezahlen von Hexagon und Tetraktys. Einbezogen wird auch das 5*5-Punkte Quadrat mit seinen 16 Einzelquadraten.

3. Die horizontal und vertikal berechneten FS ergeben meist paarweise Zahlenverhältnisse, z.B.:

	R1	R4	sm	R2	R3	sm	Verh.
li./hor.	92	76	168	110	52	162	6*(28:27)
li./vert.	65	70	135	64	131	195	15*(9:13)
	R1	R2		R3	R4
re./hor.	148	167	315	205	96	301	7*(45:43)
re./vert.	149	148	297	208	111	319	11*(27:29)
	R1	R3		R2	R4
re./vert.	149	208	357	148	111	259	7*(51:37)

4. Es sollte nicht verwundern, daß auch die 4 in den beiden Grafiken ermittelten Summen durch 11 teilbar sind:

	ZS	FS	sm
aufst.	614	330
FW	309	21	330
abst.	1190	616
FW	31	24	55
330:55 = 55*(6:1)

Der gemeinsame Teiler 55 ist die Summe der Zahlen 1-10.

Erstellt: August 2009

domum

index