Die Zahl 35
III. Die 3 Achsen des Hexagons
IV. Die Achsen im Tetraktysstern
V. Das Verhältnis der Kreisflächen
VI. 3:5 und 5:7 in Tetraktys und Doppelraute
4. Die wunderbare Brotvermehrung
VIII. Die Achsenkreuze 2 und 3
XI. Das Oktaeder-Netz
Einleitung
1. Zentrale Bezugspunkte für die Zahl 35 sind die Buchstaben I und V, der Tetraktysstern, die Doppelraute (DR), das
5*5-Punkte-Quadrat (5*5PQ) mit dem Achsenkreuz 3 und die Namen der Kapitolinischen Trias.
2. In der römischen Geschichte ist die
Zahl 35 besonders von den 35 TRIBUS bekannt, 4 städtischen (urbanae) und 31 ländlichen
(rusticae). Bereits im Jahr 241 v.Chr. wurde dieser endgültige Stand erreicht.
Jeder spätere Gebietszugewinn wurde einem dieser Tribus zugewiesen. Die Zahl 35
muß also als für eine absolute Größe gegolten haben.
3.
Wie
ich an anderer Stelle dargelegt habe, gewinnt das
Dezimalsystem im Oktaeder
seine dreidimensionale Vollendung. Das Oktaedernetz besteht aus 35 Elementen, 10 Punkten, 8 Dreiecken und 17
Linien:
|
|
4. Die folgenden Ausführungen wollen
der Bedeutung der Zahl 35 auf die Spur kommen.
1. Die Buchstaben IV sind zugleich Zahlzeichen (ZZ).
Als Buchstaben haben sie den ZW 9+20 = 29, als ZZ die Werte 1+5 = 6, zusammen
35.
2. Die beiden Buchstaben werden
meistens in ihrer alphabetischen Reihenfolge verwendet, aber auch in der
Reihenfolge VI,
etwa in allen Verben mit u-Perfekt. Zwei Gottheiten der Kapitolinischen Trias
beginnen mit IV: IVPPITER und IVNO.
3. In der Reihenfolge I-V bedeuten die ZZ die Zahl 4, in
umgekehrter Reihenfolge V-I
die Zahl 6, zusammen 10.
4. Die Form der beiden Buchstaben geben einigen Aufschluß über ihre Bedeutung. Das I besteht aus 1 Linie und 2
Endpunkten, das V aus
2 Linien und 3 Punkten. Zählt man Linien und Punkte zusammen, erhält man in
zweistelliger Zusammensetzung 35.
5.
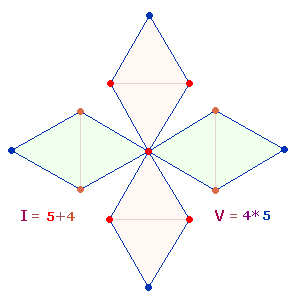
Die
Beziehung zwischen Buchstaben und Zahlzeichen ist in einer doppelten Rechnung
zu sehen: I = 5+4, V = 4*5. Der geometrische Ort hierfür ist
– neben dem Achsenkreuz 5 – im Doppelrautenkreuz zu suchen:
|
|
Zu
IV ein neuerer Beitrag (2007)
1. Die Zahl 35 besteht aus den
Faktoren 5*7, ergibt in der Addition 3+5 die Zahl 8 und als Produkt 3*5 die
Zahl 15. Die Summe der 3 Werte beträgt 35+8+15 = 58.
2. Den Zusammenhang 15 und 5*3/3*5
zeigen die 4 Einleitungsverse von Ovids Metamorphosen. Ihre Zahlensumme (ZS)
ist die Primzahl 1553.
III. Die 3 Achsen des
Hexagons
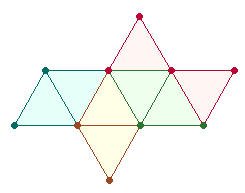
1. Als wesentlicher Ausgangspunkt für
die Zahl 35 ist die Produktbildung 3*5 für die 3 Achsenkreuze des Hexagons
anzusehen. Jede Achse besteht aus 3 Punkten und 2 Linien. Bereits hier ergänzen
sich beide ZZ I und V. Denn einer Kreisachse liegen 2
Radien aus je 2 Punkten und 1 Linie zugrunde. Das ZZ V liefert die 5 Elemente des
Durchmessers (DM), das ZZ I
den 2. Mittelpunkt.
2. Die gegenseitige Beziehung der
Werte 1 und 5 läßt sich am ehesten so verstehen, daß die 1 den Anfang und die 5
das Ende der Zahlenreihe 1 bis 5 bildet, daß sie sich symmetrisch zu einander
verhalten und aus der Addition und der Teilung durch 2 die Symmetriemitte
bestimmt werden kann.
IV. Die Achsen im
Tetraktysstern
1. Die Axiallinien des Tetraktysstern
verlaufen nicht gerade, sondern in zwei Knicken. Die 5 Durchmesserelemente des einfachen
Kreises, durch das ZZ V
vertreten, werden nun um die ZZ IV = 4 zu 9 Durchmesserelementen erweitert.
2. Nun tritt die Ergänzungsfunktion
des Buchstabens und ZZ I in
Erscheinung. Der Zahlwert 1
des ZZ bildet den Anfang, der ZW 9 des Buchstabens das Ende der 9 DM-Elemente. Durch die
Addition 1+9 = 10 werden die 9
DM-Elemente zu 2*5 Radialelemente.
Diese teilen sich auf in IV = 4
Linien und VI = 6 Punkte.
3. Im Tetraktysstern gibt es nun
einen Radius aus 3 und einen aus 5 Elementen, die der Gestalt beider
Buchstaben aus 3 und 5 Elementen entsprechen (I.4).
V. Das Verhältnis der
Kreisflächen
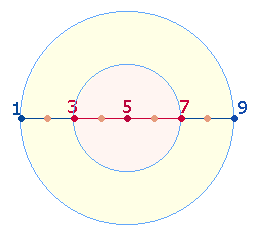
1. Wenn man um die äußeren
Schnittunkte des Tetraktyssterns einen Kreis schlägt, verhält sich die Fläche
des inneren Kreises zum erweiterten Flächenring wie 1:2 bzw. zur gesamten Fläche des
äußeren Kreises wie 1:3. Aus diesen beiden Verhältnissen entstehen durch Addition
die trinitarischen Zahlen 3
und 4 und daraus die Zahl 7. Besonders dies
beiden Flächenverhältnisse ermöglichen die Vorstellung von einem Gott in drei
Personen. Schon die 3 Achsen und 3 Doppeldreiecke des Hexagons innerhalb eines
Kreisbogens lassen eine solche Schlußfolgerung zu.
2. Dem Verhältnis 1:3 der
Kreisflächen entsprechen die Verhältnisse der DM-Elemente 5:9 und die Radialelemente 3:5. Der ZW für TRES – drei ist 59.
VI. 3:5 und 5:7 in
Tetraktys und Doppelraute
1.
Während
die Zahl 53 als Primzahl nicht teilbar ist,
setzt sich die Zahl 35 aus
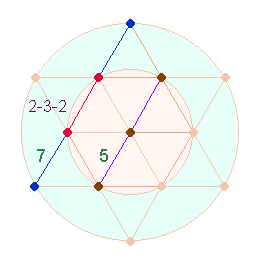
den Faktoren 5 und 7 zusammen. Diesen beiden Zahlen entsprechen die 5 Elemente
einer Hexagonachse und die 7 Elementen einer Tetraktysseite, die sich aus 3
Elementen des inneren Kriesesdurchschneidet und die Zahl 7 so in 2+3+2 bzw 4+3
unterteilt. Da sich die Tetraktysseite mit 7 Elementen den ganzen äußeren Kreis
mit der Flächengröße 3 durchschneidet, kann das Verhältnis 5:7 für das Kreisflächenverhältnis
1:3 stehen:
|
|
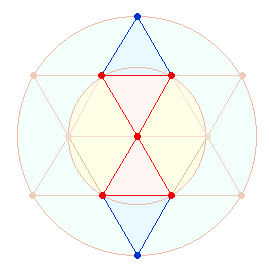
2. Deutlicher zeigt sich die
Gleichsetzung von 5:7 und 1:3 in der DR. Hier werden 5 Punkte des inneren Kreises als
Begrenzungspunkte eines Doppeldreiecks durch 2 Punkte und 2 Dreiecke erweitert:
|
|
Daher
können auch 2:2 Dreiecke als Flächenverhältnis 1:3 gedeutet werden. Dies deckt
sich besonders mit dem Problem zweier Kreishälften, die lediglich durch zwei
Durchmesserpunkte gekennzeichnet sind. Eine Kreishälfte definiert sich demnach
durch zwei Punkte + einer halberten Kreislinie und weist der zweiten halben
Kreislinie die zweite Kreishälfte zu. Ein Verhältnis 2:2 dagegen erhält man,
wenn man den 2 Punkte 2 halbe Kreislinien gegenüberstellt.
Das Verhältnis 5:2 Punkte kann man
dem Flächenverhältnis 1:2 gleichsetzen, das Verhältnis 5:(5+2)
dem Flächenverhältnis 1:3,
gleichzeitig aber auch dem Verhältnis der Radialelemente 3:(3+2) = 3:5.
Die Punkteverteilung 5+2 in der
Doppelraute ist für das Dezimalsystem von besonderer Bedeutung:
–
Eine
DM-Linie des Tetraktyssterns besteht aus 2*5 Radialelementen. Die Zahlen 5 und 2
verweisen also auf die Zahl 10 durch 2*5 und stellen den Faktorenwert durch 5+2
= 7 dar. Beide Aspekte werden besonders durch die Zahl 107 repräsentiert.
–
Die
Radialelemente 3+2,
die das Flächenverhältnis 1:2 anzeigen, stehen mit 2 und 5 durch die 5er-Potenz
von 2 in Beziehung: 2 hoch 5 = 32.
3.
Die
Grundzahlen 1 bis 9 haben 5 als konzentrische Mitte. Die
trinitarische Formel 1:3 setzt sich fort in symmetrisch gegenüberliegenden und
parallelen Verhältnissen. Die erste höhere Zahleneinheit 5 beruht auf 5 Durchmesserelementen.
Daher steht dem Verhältnis 1:3 das Verhältnis 5:3 gegenüber. In einem
Doppelkreis stehen sich die Außenverhältnisse 1:3 und 9:7 und die
Innenverhältnisse 5:3 und 5:7 gegenüber. Gegenüberliegende Zahlen ergänzen sich
jeweils zur Zahl 10, als zweistellige Zahlen addiert zu 110:
|
|
In der Zahl 35 sind die trinitarischen
Innenverhältnisse (35:53, 57:75) durch das Produkt 5*7 zusammengefaßt. Das zeigt sich
zusätzlich in der Addition der Faktorenwerte (FW) von 57>22 und 75>13, die im Produkt 5*7/7*5 = 35 zu ihrer eigenen Gestalt
zurückkehren.
Die FW der beiden konzentrischen Zahlenpaaren zeigen folgendes Bild:
|
|
ZW |
FW |
ZW |
FW |
Sm.FW |
|
|
35 |
12 |
53 |
53 |
65 |
|
|
75 |
13 |
57 |
22 |
35 |
|
Sm. |
110 |
25 |
110 |
75 |
100 |
|
|
25:75=25*1:3; 65:35=5*13:7 |
||||
Die Addition der FW der symmetrisch
gegenüber liegenden Zahlenpaare ergibt das trinitarische Ausgangsverhältnis (1:3): 25:75 = 25*(1:3) und das Verhältnis 65:35 = 5*(13:7). Die Zahl 25 enthält die
PunkteVerteilung 2:5 der Doppelraute. Das Verhältnis 13:7 bezieht sich auf die
13 Punkte des Tetraktyssterns und den 7 Punkten des inneren Kreises und
bedeutet somit das Verhältnis 3:1. Das Verhältnis FW:ZW beträgt 100:220 = 20*(5:11). Das
bedeutet in diesem Zusammenhang ein Quadrat aus 11 Durchmesserpunkten und 5
Maßeinheiten je Achsenarm. Entsprechend der jeweiligen Ergänzungssumme 110 =
11*10 handelt es sich um ein Quadrat aus 11*11 Punkten und 10*10
Quadrateinheiten.
4. Die wunderbare Brotvermehrung
Im neuen Testament wird berichtet,
wie Jesus mit 5
Broten und 2 Fischen die wunderbare
Brotvermehrung beginnt (Mt 14,17). Durch die Hinzufügung von nur 2 Punkten
werden zwei neue Flächen gewonnen und das anfängliche Doppeldreieck vergrößert
sich zu zwei Rauten, von denen jede eine gewisse Ähnlichkeit mit einem Fisch hat. Nun erweitern die 2 Punkte den inneren Kreis zunächst
um einen Flächenring von der doppelten Größe des inneren Kreises. Hinter den 5+2 Punkten liegt aber unsichtbar mit
7 Punkten ein zweites Mal der ganze
äußere Kreis bzw. stellvertretend die ganze Doppelraute. Von diesem unsichtbaren
Hintergrund aus tritt das göttliche Wirken der permanenten Teilung
gewissermaßen in die Sichtbarkeit. Wenn wir die 5 Punkte wörtlich als 5 Brote
ansehen und ein Dreieck aus 3 Punkten besteht, werden aus 5 bereits 6 Brote (Mittelpunkt zweimal gerechnet).
Da die beiden "Fischdreiecke" Anteil haben an 2
"Brotpunkten", ist an eine Vermehrung von 2 auf 6 Fische zu denken.
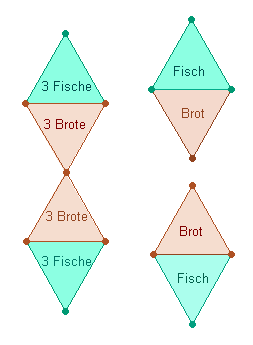
Da Brot und Fisch als gemeinsame Nahrung zusammengehören, kann man sich eine
Raute geteilt in eine Hälfte Brot und eine Hälfte Fisch vorstellen:
|
|
Zu den Zahlen 5 und 2 siehe auch: Die Null
als Vermehrungsprinzip.
1. Die Buchstaben und ZZ IV verknüpfen das Achsenkreuz 5
(AK5) mit dem 5*5-Punkte Quadrat (5*5PQ), dem das AK3 zugrunde liegt. Der
Quadratrahmen des 5*5PQ entsteht dadurch, daß ein Winkel des AK5 gegen den
anderen verschoben wird, bis die Achsenenden zusammentreffen (vgl.
AK5).
Für die Zuordnung der Bu.IV sind 2
Gesichtspunkte zu beachten:
–
Die
DM-Punkte des AK5 werden zu DM-Elemente (P+L) des AK3.
–
Punkte
oder Elemente besitzen unnumeriert und numeriert systemrelevante Bedeutung.
2.
Der
Zusammenhang zwischen AK5 und dem 5*5PQ kann am ehesten verdeutlicht werden,
wenn man die Punkte der 4 Achsenarme des AK5 vom MP nach außen (oder umgekehrt)
numeriert:
|
|
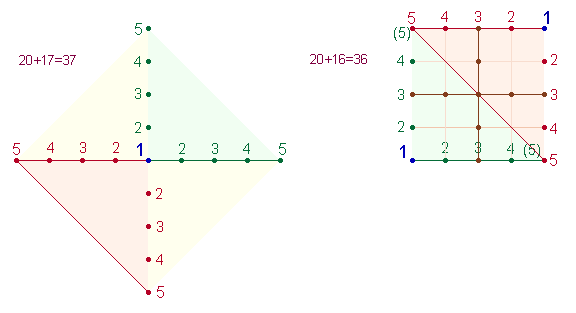
Formal werden die 4*5 Punkte des
AK5 zu 4*5 Punkten des Quadratrahmens (QR). Real jedoch besteht das AK5 aus 17P und der QR der 5*5PQ aus 16P. Addiert ergibt diese Doppelzählung
40+33 = 73.
3. Die gemeinsame Grundlage für IV bildet die konzentrische
Numerierung der Punkte des AK5. Zusammengezählt ergibt die Numerierung der 9 Punkte den Wert 29 je Achse. Dem ZW 9 für das I entspricht die Addition 5+4, dem ZW 20 für das V die Multiplikation 4*5 Radialpunkte des AK5, worauf der
Winkel V hinweist.
Die unterschiedliche
Rechenperspektive im AK5
besteht darin, daß das I alle
Punkte einer Achse umfaßt, das V
aber zu zu den 17
realen Punkten des gesamten AK5 noch die 3 entfallenen MP hinzunimmt.
4.
Diese
unterschiedlichen Rechenweisen werden im 5*5PQ modifiziert. In die Zahl 9 sind
nun die Linien mit einbezogen:
|
|
Zunächst nimmt das I die Führung, indem es den 9
DM-Elementen einen weiteren Punkt hinzufügt, um 2*5 Radialelemente zu erhalten.
Es geht also um die Ergänzung von noch Fehlendem. Das V übernimmt vom 5*5PQ 4*5 Punkte
für den QR des AK3. Wenn man diese 4*5 Rahmeneinheiten untereinander setzt,
fehlt die 5. Einheit. Sie wird als neue Symmetriemitte hinzugefügt.
5. Die 5 Punkte des AK3 werden zu 5
Elementen (3P+2L) des einfachen Kreises. Um 2*3 Radialelemente zu erhalten, muß
man einen weiteren MP hinzufügen. Die Ergänzung 5+1 leisten die beiden ZZ VI. Die beiden ZZ ergänzen sich also
untereinander und fügen dem kombinierten Wert 35 der beidenZeichen noch 6
hinzu. Die Zahl 6 und die beiden Werte des I (9+1) ergeben die 16 Quadrateinheiten im 25-Punkte-Quadrat. Sowohl 25 als auch
16 gehen auf die trinitarischen Zahlen 3 und 4 zurück, 6 und 16 aus den
Additionen 1-3 und 1-4, 25 aus seinen Konstitutiven 12+13.
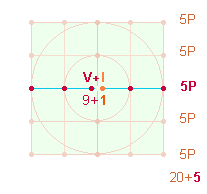
6. Durch Addition von Buchstabenwert
und ZZ-Wert ergibt sich für das I 9+1 = 10 und das V 20+5 = 25 und somit das Verhältnis 5*(2:5). Dieses Verhälnis zeigt
–
die
Umkehrungen 52 und 25,
–
die
kombinierten Werte des I
durch 2*5 = 10 und des V
durch 25.
–
Setzt
man das Verhältnis 2:5 dem I
und dem V gleich und setzt beide Buchstaben
in Beziehung zu den 2:5 Punkten der Doppelraute, wird zunächst durch IV das Flächenverhältnis 2:1
ausgedrückt. Möchte man das Verhältnis 3:1 bzw. 1:3, lauten die Formeln (I+V):V
bzw. V:(I+V). Sie entsprechen den Wortwurzeln IVV- – helfen und VIV- – leben. Menschliches Leben ist also auf gegenseitige
Hilfe angewiesen.
7.
Die
Hinzufügung eines 2. Radialmittelpunktes ist auch auf die numerierten
DM-Elemente anzuwenden. Es ergibt sich daraus eine doppelte Zählung:
|
|
Die Summe der doppelten Punktezählung beträgt 17+18 = 35.
1. Die 9 Elemente Einer DM-Linie des
Tetraktyssterns und des AK3 zeigen ein wesentliches Merkmal des Dezimalsystems:
Die 9 Grunzahlen werden durch einen 2. Radialmittelpunkt auf die Dezimaleinheit
10 erhöht. Aus den 9 DM-Elementen werden so 2*5 Radialelemente. Der enge
Zusammenhang beider drückt sich in zwei Primzahlen aus, in der Addition 10+9 =
19 und in der Zusammensetzung 109. Das Achsenkreuz des SATOR-Quadrats enthält
4T = 4*19 und der Gesamt-ZW beträgt 109.
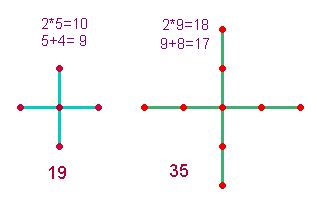
2.
Nun
geht die wichtige Zahl 19 auch aus einer Doppelzählung der Elemente des AK2
hervor: Die Gesamtzahl der Achsenkreuz-Elemente beträgt 5P+4L = 9, jede Achse
besteht aus 3P+2L = 5, die Gesamtsumme ist demnach 9+2*5 = 19:
|
|
3. Wenn nun die Tetraktys auf einer
Figur mit 2 radialen Maßeinheiten beruht und eine DM-Linie dieselbe Doppelzählung
von 9+10 zuläßt wie die beiden Achsen des AK2, dann müssen auch die analogen
Werte des AK3 wesentliche Bedeutung für das Dezimalsystem besitzen.
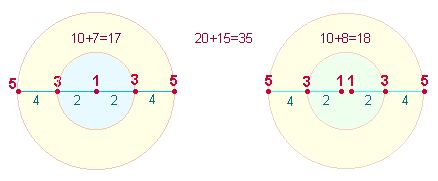
4. Analog zum AK2 lautet die
Doppelzählung für das AK3 9P+8L = 17 und 2*(5P+4L) = 18, zusammen 35. Die Zahl 35 erweist hier ihre
Grundlegung in den Elementen eines Achsenarmes: 3 Punkte und (3 Punkte + 2 Linien)
= 5
Elemente.
5. Die Zahlen 9 und 8 sind die
symmetrischen Entsprechungen zu 1 und 2 und können in deren Bedeutung verwendet
werden. Wenn also 1+2 drei Radialelemente ergeben, dann übernimmt 9+8 = 17 dieselbe Funktion. Die drei
Radialelemente erhöhen sich durch 2*9 = 18 auf 5. Das Verhältnis 17:18 bedeutet also, auf die 2
Kreisflächen des Tetraktyssterns übertragen das Flächenverhältnis 1:2. Möchte man das Verhältnis 1:3
bzw. 3:1 = 1:(2+1) bzw. (1+2):1, muß man noch einmal
17 hinzuzählen: 17:(18+17) bzw. (18+17):17 = 52.
Erstellt: April 2005