C. Symmetrien und T-Struktur des 5x5-Punkte Quadrats
I. Einleitung
III.
Anwendung auf drei Quadrate
I. Einleitung
1.
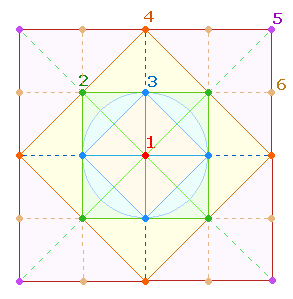
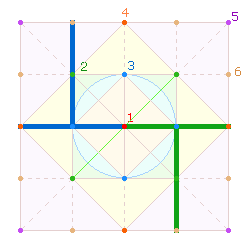
Ein 5*5 Punkte-Quadrat besteht aus 2 Quadratrahmen und 2 Rautenquadraten. Ihnen entsprechen 6 zu unterscheidende Punktegruppen:
|
|
Da bei der Quadratbildung zuerst die Diagonale in Erscheinung tritt,
habe ich die Eckpunkte des kleineren Quadratrahmens QR3 für die Nummer 2 vorgezogen. Erst ab QR3 ist eine umlaufende Numerierung von Quadratrahmen möglich.
2. Nach meiner
Überzeugung spielt der Buchstabe T eine
bedeutende Rolle im SATOR-Quadrat. Hier sollen
alle T-Formen systematisch behandelt werden. Durch Zuordnung der Punktegruppen zu
den T-Formen können numerierte Punktewerte leicht errechnet werden.
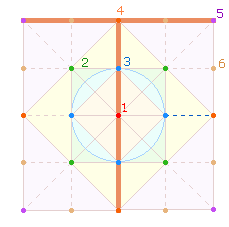
3. Es gibt
insgesamt 6 verschiedene T-Gruppen. 1 Gruppe besteht aus 9 Punkten, alle übrigen aus 5 Punkten. Die 6 Gruppen werden paarweise vorgestellt und mit einer Tabelle versehen, die
zeigt, wie häufig jeder Punkt in Anspruch genommen wird.
1. Die ersten
beiden Gruppen betreffen das innere Quadrat (Qu3) und das
äußere Quadrat (Qu5):
|
|
|
|
Gruppe |
T-Zahl |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl P |
|
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
Qu3-Hf. |
4 |
4 |
2 |
2 |
– |
– |
– |
|
|
Qu5-Hf. |
4 |
4 |
– |
2 |
2 |
2 |
2 |
|
|
Sm. |
8 |
8 |
8 |
16 |
8 |
8 |
16 |
64 |
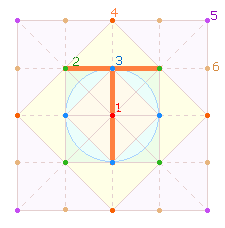
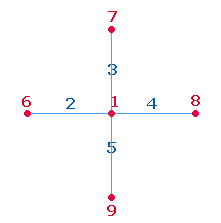
2.
Die beiden folgenden T-Gruppen haben ihren Standfuß
entweder auf der Mittelachse (max) und den Querbalken auf dem
äußeren Quadratrahmen (a) oder in umgekehrter Richtung auf der
Mittelachse (i). Für jede Quadratseite können 3 T gebildet werden, ingesamt also 12:
|
|
|
|
Gruppe |
T-Zahl |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl P |
|
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
max-a/Hf. |
12 |
4 |
2 |
3 |
3 |
2 |
2 |
|
|
max-i/Hf. |
12 |
12 |
2 |
5 |
3 |
- |
1 |
|
|
Sm. |
24 |
16 |
16 |
32 |
24 |
8 |
24 |
120 |
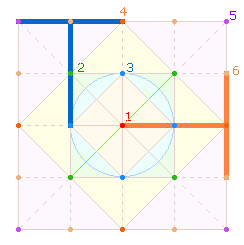
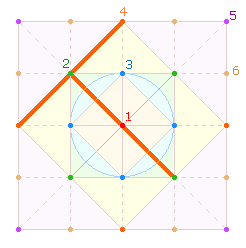
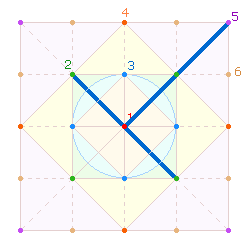
3.
Die T der 5. und 6. Gruppen legen ihren Längsbalken auf
den beiden Diagonalen und ihren Querbalken auf dem Rahmen des größeren
Rautenquadrats an. Von jeder T-Form gibt es vier:
|
|
|
|
Gruppe |
T-Zahl |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl P |
|
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
diag-a/Hf. |
4 |
4 |
2 |
– |
2 |
– |
– |
|
|
diag-i/Hf. |
4 |
4 |
3 |
– |
– |
1 |
– |
|
|
Sm. |
8 |
8 |
20 |
|
8 |
4 |
|
40 |
4.
Von den 3*2 T-Formen lassen sich 8*(1+3+1) = 40 T bilden, die insgesamt 216 = 6³ Punkte in Anspruch nehmen, für jede
Gruppe im Durchschnitt 6². Es ergeben sich für die einzelnen
Punktegruppen folgende Häufigkeiten:
|
Gruppe |
T-Zahl |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
|
Zahl P |
|
1 |
4 |
4 |
4 |
4 |
8 |
25 |
|
Häufigkeit |
40 |
32 |
11 |
12 |
10 |
5 |
4 |
74 |
|
Sm. |
|
32 |
44 |
48 |
40 |
20 |
32 |
216 |
Die Zahl 216 als 3. Potenz von 6 weist über die Quadratstruktur
hinaus auf die dreidimensionale Figur des Oktaeders hin, der aus
zwei Doppelrauten des Tetraktyssterns
zusammengefügt werden kann.
Die Aufteilung der Zahl 216 in 3
zweistellige Zahlen und ihre Summe 21+26+16 = 63 weisen auf drei
Doppelrauten von je 21 Elementen hin. Aus 26 Elementen
besteht der Oktaeder und aus 16 Linien der Rahmen eines Doppelrautenkreuzes. 4*4 = 16 Linien enthält auch
der Rahmen des Qu5.
III. Anwendung auf drei
Quadrate
1.
Die ermittelten Werte sollen nun auf 3
zusammengehörigen Quadrate angewendet werden: das numerierte 5*5 Punkte Quadrat, das 1x1-Quadrat und das SATOR-Quadrat. Neben den numerischen Werten sollen auch die Faktorenwerte (FW) erfaßt werden. Zunächst werden die Werte für die einzelnen Punktebereiche
ermittelt und dann mit dem Häufigkeitsfaktor multipliziert:
|
Gr. |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
||||||
|
Zahl P |
1 |
4 |
4 |
4 |
4 |
8 |
25 |
||||||
|
|
ZS
|
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
|
|
NQ5 |
1 |
1 |
24 |
21 |
20 |
17 |
68 |
61 |
76 |
50 |
136 |
70 |
|
|
1x1 |
5 |
5 |
20 |
18 |
– |
– |
20 |
20 |
20 |
14 |
40 |
32 |
|
|
SQ |
13 |
13 |
64 |
50 |
20 |
20 |
76 |
76 |
70 |
50 |
60 |
40 |
|
|
|
19 |
19 |
108 |
89 |
40 |
37 |
164 |
157 |
166 |
114 |
236 |
142 |
1291 |
|
|
38 |
197 |
77 |
311 |
280 |
378 |
|
||||||
|
Gr. |
MP |
G2 |
G3 |
G4 |
G5 |
G6 |
Sm. |
Sm. |
GS |
||||||
|
|
ZS
|
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
|
|
Faktor |
32 |
11 |
12 |
10 |
5 |
4 |
74 |
|
|
||||||
|
NQ5 |
32 |
32 |
264 |
231 |
240 |
204 |
680 |
610 |
380 |
250 |
544 |
280 |
2140 |
1607 |
3747 |
|
1x1 |
160 |
160 |
220 |
198 |
– |
– |
200 |
200 |
100 |
70 |
160 |
128 |
840 |
756 |
1596 |
|
SQ |
416 |
416 |
704 |
550 |
240 |
240 |
760 |
760 |
350 |
250 |
240 |
160 |
2710 |
2376 |
5086 |
|
|
608 |
608 |
1188 |
979 |
480 |
444 |
1640 |
1570 |
830 |
570 |
944 |
568 |
5690 |
4739 |
10429 |
|
|
1216 |
2167 |
924 |
3210 |
1400 |
1512 |
|
|
|||||||
Hervorzuheben ist die FS des SATOR-Quadrats 2376: Sie ist durch 216 teilbar, sodaß jeder belegte Punkt den
Durchschnittswert 11 besitzt. Tatsächlich sind alle zusammengesetzten Werte des SATOR-Quadrats
durch 11 teilbar: 69+52 = 121 = 11*11; 52+61+52 = 165 = 15*11.
Die
Aufteilung der Zahl 2376 in 23+76 zeigt der Zahl 76 = 4*19 = die 4 T des TENET-Kreuzes und ihren FW 23. Die Summe 23+76 = 99 = 9*11 weist auf zwei Achsenkreuze mit einem und
3 Mittelpunkten hin:
|
|
|
Auch die Zahl
19 hat als Modell ein Achsenkreuz aus 3 Mittelpunkten:
Erstellt:Februar 2008