21 Primzahlen von 11 bis 97

47 als Symmetriemitte

I. Einleitung

II. Bedeutung der Zahl 47

III. 21 Zahlen auf dem Tetraktysrahmen

IV. 21 Zahlen auf der Doppelraute

V. 18 Zahlen auf dem Tetraktysrahmen

VI. Bedeutung der Zahl 149

I. Einleitung

Reihe 1	0-9	1		7
Reihe 2	11-19	1	3	7	9
Reihe 3	21-29		3		9

1. Vorstehendes Primzahlmuster der ersten drei Zehnerreihen mit 8 Primzahlpositionen wird auf zweistelliger Ebene zwischen 11 und 100 dreimal durchbrochen (X):

ZR	Pos.	1	3	7	9
2	11-20	11	13	17	19
3	21-30		23		29
1	31-40	31		37
2	41-50	41	43	47	X
3	51-60		53		59
1	61-70	61		67
2	71-80	71	73	X	79
3	81-90		83		89
1	91-100	X		97

Von den 3*8 Primzahlpositionen sind 21 mit Primzahlen besetzt. Die Zahl 47 bildet als 11. Primzahl (PZ) die Symmetriemitte.

2. Die Summe der drei Gruppen ist 180+371+492 = 1043 = 7*149. Die Mittelgruppe besteht aus 7 Primzahlen, ihr Durchschnittswert ist 53, der auch in der Addition der beiden Zahlen 47+59 = 106 enthalten ist. Die Bedeutung der Zahl 53 besteht unter anderem darin, daß sie sich unter anderem aus 49 Elementen des Tetraktyssterns + 2 Kreisbögen + 2 Kreisflächen zusammensetzt.

Wie weiter unten zu zeigen ist, wird durch Anordnung der 21 Primzahlen auf den drei Tetraktysseiten die Summe 1043 im Verhältnis 4:3 geteilt.

II. Bedeutung der Zahl 47

1. Die Bedeutung der Zahl 47 ist hauptsächlich aus ihren einstelligen Ziffern 4 und 7 zu ermitteln. Die Grundvoraussetzung für das Verständnis dieser und aller Zahlen ist das komplementäre Zusammenwirken von Maßeinheiten und deren Begrenzungspunkten, die – zusammen mit auftretenden Flächen – als ELEMENTE bezeichnet und gezählt werden. Wenn man davon ausgeht, daß sich das Dezimalsystem aus dem Mittelpunkt des Kreises entwickelt, vereinen die Zahlen 4 und 7 etwa sechs Modelle in sich:

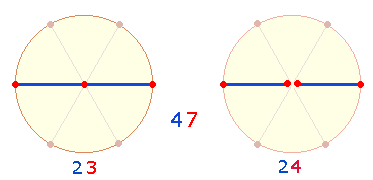
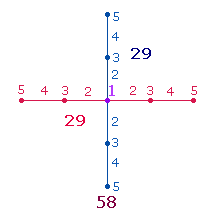
a) Der Kreisdurchmesser eines Kreises besteht aus zwei Radiallinien, die jeweils durch 2 Punkte begrenzt werden, so daß die beiden Radien die Summe 2*3 = 6 ergeben. Der Durchmesser selbst aber besteht aus 5 Elementen, sodaß, um beiden Aspekten zu genügen, beide Summen zu 11 zu addieren sind. Zählt man Maßeinheiten (Radialmaße) und Punkte getrennt, ergibt sich das Verhältnis 4:7, das in folgender Grafik veranschaulicht ist:

In zweistelliger Zusammensetzung der zweifachen Maßeinheiten und Punkte sind 23 und 24 die Konstitutivzahlen ihrer Summe 47. Die Zahlensummen (ZS) und Faktorensummen (FS) der Zahlen 1-23 und 1-24 sind (276+201) + (300+210) = 477+510 = 987 = 21*47 = FW 57. Die Zahlen 9 8 7 sind Komplementärzahlen zu den ersten drei Zahlen 1 2 3, haben somit trinitarische Bedeutung. Die Konstitutiven 23 und 24 führen über ihre ZS+FS zu ihrer Summe 47 zurück.

Die Zahlen 23 und 24 haben ein Modell in der Numerierung des Doppelrautenkreuzrahmens.

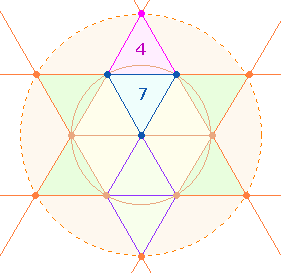
b) Die pythagoreische Tetraktys mit ihren 10 Punkten ist als Erweiterung der Segmentlinien des Hexagons zu verstehen. Dabei erfahren die 6 gleichseitigen Dreiecke eine spiegelbildliche Fortsetzung, die 6 Rautenfiguren ergibt. Die 7 Elemente eines Dreiecks werden jeweils um 4 weitere Elemente erweitert. Drei sanduhrfömige hexagonale Doppeldreiecke werden zu drei Doppelrauten fortentwickelt:

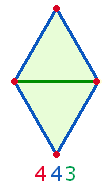
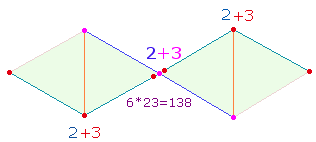
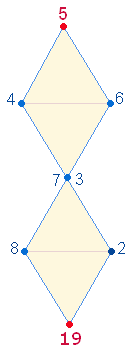
Eine Doppelraute (DR) besteht nun aus 21 Elementen: 7 Punkten, 10 Linien und 4 Dreiecken.

In den 21 Elementen der DR verdichtet sich die Bedeutung der Zahlen 4 und 7: Die Summe der Zahlen 1-7 ist 28 = 7*4. Alle vier Einzelziffern des Ergebnisses sind in der DR enthalten: 2 Querlinien, 8 Rahmenlinien, 7 Punkte und 4 Dreiecksflächen. Es entsteht das Verhältnis 3:4 zwischen 21 realen Elementen und 28 Elementen von 4 Dreiecken aus je 7 Elementen.

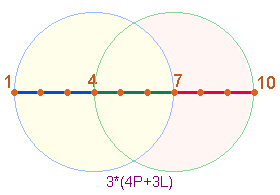
c) 10 Punkte auf einer Strecke begrenzen 9 Maßeinheiten. Diese 19 Elemente werden durch zwei Kreise im 4. und 7. Punkt zu 3*7 = 21 Elementen geteilt:

Die Kreismittelpunkte 4 und 7 markieren drei Strecken: 1-4, 4-7, 7-10. Jede Strecke besteht aus 4 Punkten und 3 Maßeinheiten.

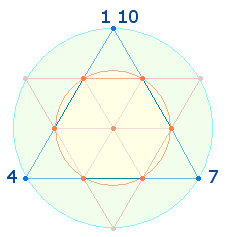
d) Die gleiche Einteilung zeigen auch die drei Seiten einer Tetraktys:

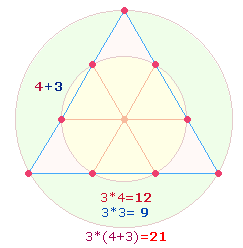
Wenn man 3*4 Punkte für den Tetraktysrahmen ins Verhältnis zur Gesamtsumme der 3*7 = Elemente setzt, erhält man das Verhältnis 12:21 = 4:7. Die 21 Primzahlen eignen sich daher besonders für eine Anordnung auf den drei Tetraktysseiten.

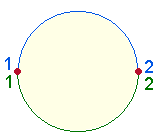
e) Die Umkehrzahlen 12 und 21 bezeichnen den Rückkehr zum Ausgangspunkt eines zweigeteilten Kreisbogens:

Addiert man die 36 aufsteigenden und 36 absteigenden zweistelligen Zahlen (13/31 usw.), erhält man wie bei 12:21 das Verhältnis 4:7: 1440:2520 = 360*(4:7).

f) Besondere Bedeutung für das Dezimalsystem haben das einfache und das hexagonale Achsenkreuz, da beide zusammen 4+6 = 10 Radialmaße enthalten:

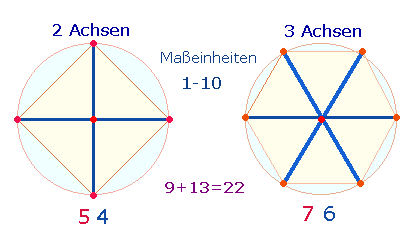
Zählt man für jede Achse 5 Durchmesserelemente, erhält man die Summe 25. Rechnet man den Mittelpunkt nur einfach, entfallen 1+2 Mittelpunkte. Die Doppelzählung 22+25 bzw. 9+10=19 + 13+15=28 ergibt 47.

g) Die Bedeutung der Zahl 47 zeigt sich bereits in den 15 vorhergehenden Primzahlen von 1–43: Deren Summe ist 282 = 6*47. (s.a. Primzahlen 2 3 5). Das Verhältnis der ersten 11 Primzahlen einschließlich 47 zu den übrigen 10 ist demnach 329:714 = 7*(47:102).

III. 21 Zahlen auf dem Tetraktysrahmen und dem Kreisbogen

a) auf dem Tetraktysrahmen

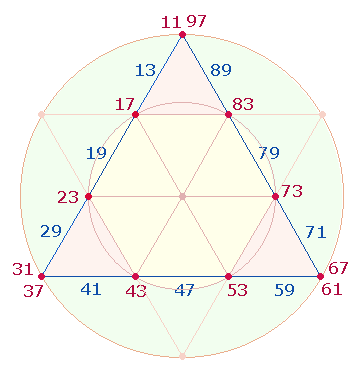
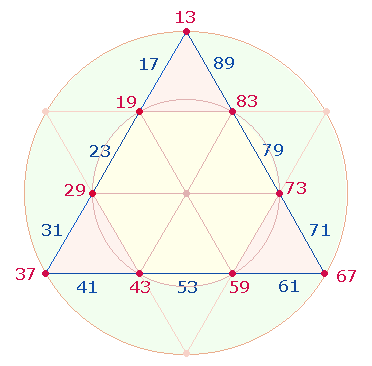
1. Entsprechend der oben dargelegten Aufteilung der 21 Elemente des Tetraktysrahmens in 3*7 lassen sich die 21 Primzahlen auf den drei Tetraktysseiten anordnen:

Das herausragende Ergebnis dieser Anordnung ist, daß entsprechend dem Verhältnis von 3*4 Punkten zu 3*3 Linien das Summenverhältnis 596:447 = 149*(4:3) beträgt. Beteiligt sind dabei zweimal die Summen 96 und 98. (23+73, 43+53; 31+67, 37+61).

Drei Primzahlen kommen also jeweils auf die durchschnittliche Summe 149. Je 3 der 9 Linien-Zahlen lassen sich zu 149 addieren:

13	89	47
29	41	79
59	71	19

Jede Dreiergruppe gehört zu einer "Fischfigur". Die Summe der Einzelziffern ist jeweils 32. Von den übrigen 12 Zahlen läßt sich die Summe 149 nur einmal in zwei Varianten zusammensetzen: 23+53+73 oder 23+43+83. Die Quersumme ist in diesen Fällen die Umkehrzahl 23. Man kann hier an die Summe 55 der Zahlen 1-10 denken, die in der numerierten Tetraktys in die beiden Umkehrzahlen aufteilbar ist.

Das trinitarische Prinzip des Verhältnisses 3:1:3, das in der Punkteverteilung der Doppelraute erkennbar ist, zeigt sich hier in seinem doppelten Aspekt: Die dreimal 149 als Einzelsummen kommen den drei göttlichen Personen gesondert zu, die vierte Summe kann als Einheit in der Dreiheit gelten.

Die Summe aller Einzelziffern beträgt 197.

2. Ohne die obige Aufteilung der 21 Primzahlen auf Punkten und Linien des Tetraktysrahmens lassen sich nicht mehr als 5 Dreiergruppen mit der Summe 149 zusammenstellen. Dies ist nachweisbar durch Summe der 21 Endziffern: 5*1+6*3+5*7+5*9 = 103. Die Endziffer 9 ist erreichbar z.B. durch 1+1+7 = 9, 3+3+3 = 9, 1+9+9 = 19 und 3+7+9 = 19. Es gibt keine Kombination der Endziffernsummen 9 und 19, die die Gesamtsumme 103 ergeben. Diese besteht entweder aus a) 3*9+2*19 = 65, b) 2*9+3*19 = 75 oder c) 9+4*19 = 85, stets bleibt als Rest die Endziffer 8, Hinweis auf 2*149 = 298:

a)				b)				c)
11	41	97	9	11	41	97	9	11	41	97	9
61	71	17	9	31	71	47	9	13	47	89	19
13	53	83	9	23	67	59	19	23	67	59	19
31	29	89	19	43	17	89	19	53	17	79	19
43	47	59	19	83	37	29	19	83	37	29	19

Eine Liste aller 29 Dreiergruppen, die ich gefunden habe, sind an anderer Stelle aufgeführt.

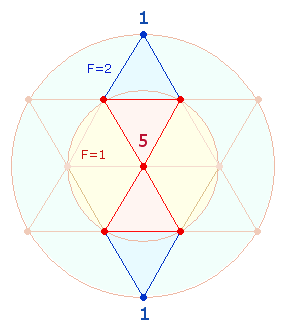
Ein tieferer Grund für die das Verhältnis von 5:2 Summen könnte in den 5 hexagonalen und 2 Erweiterungspunkten der DR liegen. Der FW 151 von 298 = 2*149 weist auf diese Punkteverteilung hin:

Die Quersummen der Dreiergruppen 23 und 32, aufgeteilt in Zehner- und Einerstellen sind 14+9 und 13+19. Zusammengezogen und in der Umkehrung erhält man 149+1319 = 1468 und 914+1913 = 2827. Ein bemerkenswertes Umkehrergebnis von 149 ergibt die ZW/FW-Verrechnung:

			sm	FW
ZS	1468	2827	4295	864
FW	371	268	639	77
sm				941

941 ist ebenfalls eine Primzahl. Der Zusammenhang mit den Dreiecken der Tetraktys wird somit erkennbar.

3. Auch die Punktezahlen können den je 3 Werten der drei ermittelten Fischfiguren – oben Mitte, unten links, unten rechts – zugeordnet werden. Es ergeben sich folgende Summen:

	3*3 L	3*(3*2) P
o.M.	149	108	100	96	453
u.l.	149	68	66	156	439
u.r.	149	128	126	40	443
sm	447	304	292	292	1335
1335 = 15*89

Die Ergebnisse weisen auf die DR hin: 1335 kann verstanden werden als 3:5 Radialelemente, die das Kreisflächenverhältnis 1:3 wiedergeben. Der DR-Rahmen besteht aus 15 Elementen, kann aber durch umlaufende Numerierung auf 8+9 = 17 Elemente erweitert werden. 89 ist auch auf 17 Elemente der Fischfigur beziehbar.

453 = 3*151 gibt die Punkteverteilung von 3 DR wieder, 439 4*3 "Dachelemente" und 9 Mittelelemente der DR. Die Einzelziffern von 443 sind auf die 11 Elemente der Raute beziehbar:

Einzelergebnisse weisen meist sowohl auf die Tetraktys als auch auf die DR hin. Dies wird bei der ZW/FW-Verrechnung erkennbar:

				sm	FW	sm	FW	sm	FW
ZS	453	443	439	1335	97
FW	154	443	439	1036	48
sm				2371	145	2516	58
FW				2371	34	2405	55
sm						4921	113	5034	844
						63	113	176	19
sm	1036 = 2*518 = 28*37; 2405:2516 = 37*(65:68) = 7*19*37								863

Auffällig ist der dreimalige Faktor 37, dem die Elemente der Tetraktys entsprechen. Die Faktoren 7*19*37 geben die Elemente der aufaddierten drei Dreiecksebenen der Tetraktys wieder:

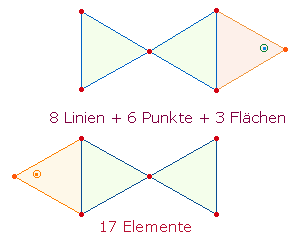
Die Einzelziffern der Primzahl 863 gibt die 17 Elemente der Fischfigur wieder:

IV. 18 Zahlen auf dem Tetraktysrahmen

1. Die drei Punktezahlen der Vertikalachse der Doppelraute sind 11+47+97 = 155. Wenn man sie in einer zweiten Rechnung wegläßt, lassen sich 18 Zahlen wiederum auf dem Tetraktysrahmen anordnen, jedoch ohne Verdoppelung auf den Eckpunkten:

2. Die Gesamtsumme 888 = 24*37 = 6*(4*37) bedeutet, daß die durchschnittliche Summe von 3 Zahlen 148, beträgt, so wie bei 21 Zahlen die Durchschnittsumme von 3 Zahlen 149 war.

Auffällig ist, daß 6 spiegelsymmetrische Paare, je zur Hälfte auf den Punkten und den Linien, die Summe 102 = 6*17 ergeben: 19+83, 23+79, 29+73, 31+71, 41+61, 43+59. Die Gleichheit von je 3*102 = 18*17 auf den Punkten und Linien ist auf die "Fischfigur" aus je 17 Elementen zu beziehen, von denen in den beiden Tetraktys und den drei DR jeweils 6 enthalten sind.

Übrig bleiben 17+89+53 = 159 = 3*53 und 13+37+67 = 117 = 9*13 = 3*39, zusammen 3*(53+39) = 3*92 = 276 = 12*23, die Summe der Zahlen 1-23. Die Einzelziffern des Faktors 23 sind als hexagonale Durchmesserelemente und zweimal als Radialelemente der DR zu verstehen:

Bei 4 Zickzacklinien des DR-Kreuzes ist 3*(2+3) zu vervierfachen. Im SATOR-Quadrat ist die ZS der 4 äußeren Quadratseiten 4*69 = 276.

3. Die Zahlen auf den 3 hexagonalen und 6 Erweiterungs-Linien ergeben 155*(1:2) = 465 = 15*31, die Zahlen auf den 6 hexagonalen und 3 Erweiterungspunkten 306+117 = 9*(34+13) = 423 = 3*141 = 9*47. Damit zeigt sich in den beiden Summen, daß die drei Zahlen 11+47+97 = 155 von Anfang, Mitte und Ende den Durchschnitt aller Zahlen repräsentieren.

4. Die 3*3 Linienzahlen der drei Fischfiguren ergeben 151 (l.u.), 159 (Mi.), 155 (r.u.), die Einerziffern wiederholen die symmetrischen Abstände 1 5 9 der mittleren Summe 159. Die durchschnittliche Summe der beiden Anordnungen von 21 und 18 Zahlen auf den Tetraktysseiten beträgt also für die jeweils 3*3 Linienzahlen 149+155 = 304 = 16*19, zusammen 3*16*19 = 912. Die ZW/FW-Verrechnung der 6 Summen ergibt:

	3x149				sm	FW	sm	FW
ZS	447	151	159	155	912	30
FW	447	151	56	36	690	33
sm	18*89; 3*555 = 45*37				1602	63	1665	48
FW					97	13	110	18
sm	30:33 = 3*(10:11); 48:18 = 6*(8:3)							66

912, aufgeteilt in 9+12 gibt wiederum die Zahl von 3*3 Linien und 4*3 Punkten der drei Tetraktysseiten wieder.

Das Verhältnis 3*(10:11) bezieht sich auf drei DR in der Aufteilung von 10 Linien und 7 Punkten + 4 Dreiecksflächen. Dasselbe ist der Fall bei der Summe der Komplementärzahlen 97+13 = 110 = 10*11. 66 = 6*11 bezeichnet die 6 Rauten des Tetraktyssterns im Verhältnis von 8 Rahmen- zu 3 Binnenelementen:

Ohne die Summe 155 der rechten Fischfigur bleibt für 6 Linien 306 = 17*18 wie für die 6 hexagonalen Punktezahlen. Die Summe der Faktoren für 306 (17+18) und 304 (16+19) ist jeweils 35 und weist auf ein Achsenkreuz AK5 mit 2 Mittelpunkten hin. Den Zahlen 18 und 17 entsprechen die Eckbuchstaben SR des SATOR-Quadrats .

5. 155 ist die FS der Zahlen 1-20, 3*155 die ZS der Zahlen 1-30. Die Aufteilung 1:2 besagt, daß jede von 10 Maßeinheiten durch 2 Punkte begrenzt wird. Andererseits sind 10 Maßeinheiten auch in den Zahlen 1-21 im Wechsel von Punkten und Maßeinheiten enthalten, sodaß sich in der Addition 20 Maßeinheiten und 31 Begrenzungspunkte entsprechen. 20 Punkte der beiden Tetraktys können somit auch als 20 Maßeinheiten aufgefaßt werden.

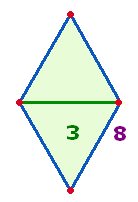
6. 53 und 5*31 der mittleren Fischfigur zeigen eine Entsprechung von 5:3 Radialelementen zum Kreisflächenverhältnis 3:1. Die Einzelziffern der Zahl 47 bedeuten das Kreisflächenverhältnis 1:3, wenn das äußere Dreieck der Raute die 3 Elemente der hexagonalen Segmentlinie einschließt und für den hexagonalen Teil der Raute nur 4 Elemente übrig bleiben:

Die übrige Hälfte von 4 Elementen erhält so durch Umkehrung aus 74 zu 47 die Führung.

7. Das ZS-Verhältnis der Linienzahlen der Hypothenuse zu den beiden Katheten ist 155*(1:2). Ebenfalls 1:2 ist das Verhältnis der ersten 5 zu den restlichen 4 Punktezahlen: 141:282.

Die ZS 210 der Zahlen 1-20 setzt sich aus 10-mal der konzentrischen Summe 21 zusammen. Die FS 155 der Zahlen 1-20 bedeutet, daß 5+5 Maßeinheiten durch 5+5+1 Punkte begrenzt werden.

Die Faktoren der beiden Summenzusammensetzungen 31+47 = 78 und 53+13 = 66 bzw. 31+53 = 84 und 47+13 = 60 haben die Verhältnisse 6*(13:11) und 12*(7:5).

8. Der Doppelaspekt von 21 und 18 Elementen des Tetraktysrahmens bildet eine zusammengehörige Einheit. Die Addition der Punkte- und Linienzahlen ergibt 596+423 = 1019 und 447+465 = 912. Die Primzahl 1019 ist interpretierbar als 10 und 1+9 Punkte von zwei Tetraktys, 9+12 als Doppelaspekt von 9 und 12 Punkten des Tetraktysrahmens. Die ZW/FW-Verrechnung der beiden Summen ergibt:

			sm
ZS	1019	912	1931
FW	1019	30	1049
sm			2980

1931 und 1049 sind Primzahlen, das Ergebnis 2980 ist daher absolut. Es bedeutet die Durchschnittszahl 149 für 20 Punkte zweier Tetraktys. Die Zahlen 19 und 31 setzen sich aus den Zahlen 12 und 21 und ihren FW 7 und 10 zusammen. Die Umkehrzahlen 12 und 21 entstehen durch die Addition der Teilsumme von 12 Punkten und der Gesamtsumme von 12 Punkten + 9 Linien des Tetraktysrahmens. Ähnliches gilt für 12 "Dachelemente" und 9 Längselemente der DR.

9. Auch die Linien- und Punktesummen der drei Fischfiguren der beiden Anordnungen sind auf ihre Zusammengehörigkeit überprüfbar:

	21	18	sm	sm	21	18	sm
u.l.	439	416	855	30	439	23	462
Mi.	453	386	839	839	154	195	349
u.r.	443	392	835	835	443	20	463
	1335	1194	2529	1041	1036	238	1274
2529 = 9*281 >287; 1041 = 3*347 >350; 1274 = 2*7²*13

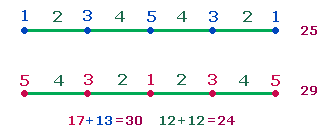
Die Zahlen 25 und 29 der Gesamtsumme 2529 stellen gegenläufige Numerierungssummen von 1-5 auf 9 Durchmesserelementen dar:

Die FS 1274 der 6 einzelnen ZS verbindet 13 und 14 Punkte des Tetraktyssterns, einmal mit einem und einmal mit einem zweiten Mittelpunkt, der die Eigenständigkeit des äußeren Kreises herstellen soll. Der Faktor 281 ist als 28+1 auf die Numerierungssumme 29 und auf 29 Elemente des DR-Kreuzes zu beziehen.

Die FW der Gesamt-ZS 2529 und der FS 1041 der 3*2 addierten Einzelsummen ergeben durch 287+350 = 637 genau die Hälfte von 1274. Zweimal die Gesamt-ZS und die beiden FS lassen sich addieren: 2529+2529 + 1041+1274 = 7373. Man erhält zweimal als Einzelziffern die 7 hexagonalen Punkte und die 3 Eckpunkte der Tetraktys.

Bei der Summenberechnung der zweimal drei Fischfiguren verdoppelten sich die hexagonalen Punktezahlen. Sie betragen 292+306 = 598 = 2*299 = 2*13*23 >38. Die Zahl 299 vereint 9 Durchmesserelemente mit der Numerierungssumme 29. 2*13 Radialelementen und 23 Durchmesserelementen entsprechen jeweils 7 Kreisflächeneinheiten. Der FW 38 = 2*19 gibt zweimal 9 Durchmesserelemente und 5+5 Radialelemente wieder. Die ZW/FW-Verrechnung der beiden Summen ergibt:

			sm	FW	sm	FW
ZS	292	306	598	38
FW	77	25	102	22
sm			700	60	760
FW			21	12	33
sm					793	74
793 = 13*61; 22:38 = 2*(11:19)

Die FS 102 = 2*3*17 stellt zwei Tetraktys mit je 3 Fischfiguren dar. Der FW von 700 ist 3*7 und auf die Elemente der drei Tetraktysseiten beziehbar. Dem FW 12 entsprechen 3*4 Punkte der drei Tetraktysseiten. Der FW 74 verweist auf zweimal 37 Elemente zweier Tetraktys. Das Produkt 13*61 ist als 7 hexagonale Punkte und 13 Punkte des Tetraktyssterns in der Bedeutung von 1:3 Kreisflächeneinheiten zu verstehen. Das Verhältnis 11:19 = (5+6):(9+10) bezeichnet den Doppelsaspekt von Durchmesser- und Radialelementen des Hexagons und des Tetraktyssterns.

598 zur Summe 1019 der Punktezahlen hinzugefügt ergibt 1617 = 33*49 >14+14 = 28, der FW der Liniensumme 912 ist 30. Das Verhältnis der beiden FW 2*(14:15) = 2*29 ist wiederum auf die Numerierungssumme von 9 Durchmesserelementen zu beziehen, jedoch auch auf ein entsprechendes Achsenkreuz mit je einem Mittelpunkt:

10. Der Doppelaspekt von 18 und 21 Elemente des Tetraktysrahmens bedeutet einen Zuwachs von 3 Elementen, der sich in der römischen Rechtsformel SC = SENATUS CONSULTO – durch Senatsbeschluß niedergeschlagen hat:

	ZS	FS	sm	FW1	FW2	sm	GS
SENATUS	94	63	157	49	13	62	219
CONSULTO	112	81	193	15	12	27	220
	206	144	350	64	25	89	439

Die 4Werte-Summen 219 und 220 sind Konstitutivzahlen für ihre Summe 439, die als 4*3 Dachelemente + 9 Längselemente der DR zu sehen sind, aber auch – mit Nachstellung der 4 als 3*4 Punkte + 9 Linien des Tetraktysrahmens. 439 ist eine Primzahl ebenso wie 349.

Die Umkehrung 349 als FS kommt folgendermaßen zustande: Es wurde oben festgestellt, daß die ZS 888 der 18 Primzahlen die Durchschnittszahl 148 für je 3 Primzahlen ergibt analog zu 149 bei 21 Primzahlen. Es können also die FS der ZS 6*148 und 6*149 gebildet werden, übrig bleibt 1*149. Die entsprechenden FW sind 46+154+149 = 349.

349 als FW ergibt sich auch aus der ZS+FS der Zahlen 1-18 und 1-21:

	ZS	FS	sm	FW1	FW2	sm	GS
1-18	171	127	298	25	127	152	450
1-21	231	165	396	21	19	40	436
	402	292	694	46	146	192	886
694 = 2*347 >349; 886 = 2*443

Die Primzahl 443 ist auf die 11 Elemente der DR zu beziehen, worauf oben bereits hingewiesen wurde:

Es wird erkennbar, daß Tetraktys und DR ontologisch in enger Beziehung zueinander stehen. 694 ist die FS der Zahlen 1-49, also der Elemente des Tetraktyssterns.

V. Bedeutung der Zahl 149

1. Die Zahl 149 ist die Summe der Umkehrzahlen 19 und 91 und ihrer FW:

			sm	FW	sm	FW	sm
ZS	19	91	110	18
FW	19	20	39	16
sm			149	34	183	64
FW			149	19	168	16
sm					351	80
FW					22	13	35
16:64 = 16*(1:3)

Die Einzelziffern von 22 und 13 geben die Entsprechungen von Kreisflächeneinheiten 2+1 und Radialelemente der DR wieder. 13 ist außerden der FW von 22.

Die Zahl 19 ist sowohl auf die Tetraktys als auch auf die DR beziehbar:

· Die Tetraktys besteht aus 10 Punkten und 9 Dreiecken. Die Einzelziffern 1+9 geben den Mittelpunkt und 9 Punkte des Tetraktysrahmens wieder:

· Eine Zickzack-Durchmesserlinie der DR besteht aus 5 Punkten + 4 Linien, also 9 Durchmesserelementen, und aus 5+5 Radialelementen:

Die Faktoren der Zahl 91 geben 7:13 Punkte des Tetraktyssterns in der Bedeutung von 1:3 Kreisflächeneinheiten der beiden konzentrischen Kreise wieder. Die Einzelziffern von 19 und 91 können als jeweils 10 Radialelemente interpretiert werden und bilden so einen DR-Rahmen. Bei achtförmiger Numerierung der DR-Punkte stehen am Ende 1 und 9 nebeneinander:

2. Weitere Bedeutungen der Primzahl 149 sind aus ihren Einzelziffern zu ermitteln:

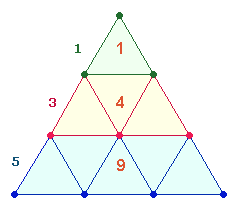
a) Die Einzelziffern beziehen sich auf drei eigenständige Ebenen von 1, 4 und 9 Dreiecken der Tetraktys:

Theologisch gesehen sind die Zahlen 1, 4, 9 als Quadrate der Zahlen 1, 2 und 3 auf die drei göttlichen Personen bezogen (deren Widerspiegelung das Dezimalsystem ist). Jede weitere Ebene des Zahlendreiecks erweitert sich um 2 Quadrate: 1+3 = 4; 4+(3+2) = 9; 9+(3+2+2) = 16 usw. Das Ergebnis ist jeweils eine Quadratzahl.

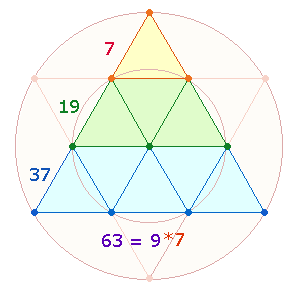
Die fortlaufende Addition der drei Ebenen für alle drei Elemente (Punkte, Linien, Flächen) ist 7+19+37 = 63. Das Verhältnis der 14 aufaddierten Dreiecke zur Restsumme ist demnach 14:49 = 7*(2:7). Außerdem ist 14 der FW von 49, also gewissermaßen der Kern der Tetraktysgestalt.

Auch der FW der 3-stelligen Zusammensetzung 135 ist 14 und führt durch Addition zu 149.

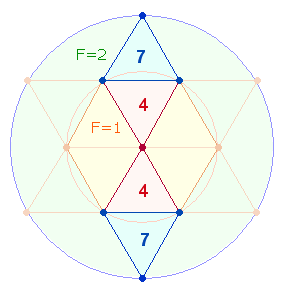
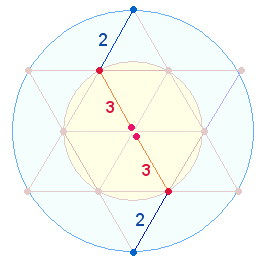
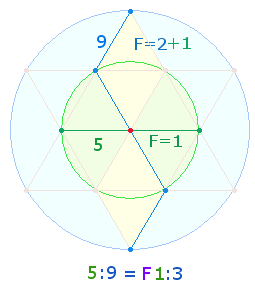
b) Die zweite Bedeutung bezieht sich auf das analoge Verhältnis der Durchmesser-(DM) Elemente zu den Flächen der beiden konzentrischen Kreise des Tetraktyssterns. Wie die folgende Grafik zeigt, repräsentieren die 1+4 DM-Elemente des hexagonalen Kreises zu den 4 Elementen der Erweiterung das Flächenverhältnis 1:2 des inneren Kreises zum äußeren Kreisring, die DM-Elemente 5+(5+4) das Verhältnis 1:3, was zusammen 7 Flächeneinheiten ergibt:

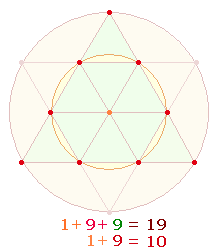
Den beiden Flächenverhältnissen 1:3 und 1:2 entsprechen 5+9 = 14 und 5+4 = 9, zusammen 23 DM-Elemente. Die Folge von 1+4+9 Dreiecken kann also auch aufgeteilt werden in 14+9. 9 ist gleichzeitig der FW von 14.

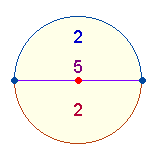
c) 1+4 = 14 ist das Ergebnis der ersten Kreisdifferenzierung durch Kreisteilung:

Der Durchmesser teilt den Kreis in zwei Kreislinien und zwei Flächen. Jede Hälfte besteht demnach aus 7 Elementen, der ganze Kreis aus 9 Elementen. Daraus ergibt sich die Addition 14+9 = 23. Die Zahlenfolge 2-5-2 entspricht den DM-Elementen der beiden Tetraktyskreise.

1. Von 11 bis 100 sind es 90 Zahlen. Die 21 Primzahlen stehen darin in Beziehung zu den restlichen 69 Zahlen, daß deren FS 8*149 beträgt. Die Zahlen 7 und 8 können den Punkten und Linien des Doppelrautenrahmens zugeordnet werden.

Erstellt: November 2010

Überarbeitet: Juni 2011

Ergänzt: Juni 2018

Inhalt II