Die Zahlen 13-97 auf 7 Punkten der Doppelraute

III. 43 Zahlen in zwei Doppelrauten

a) 7, 21, 22 Zahlen

b) 7 Zahlen, 7 Wörter

c) Einzelberechnungen

e) Zwei Hälften und das Ganze

	1		2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	253
	55	o.Z.	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	1386
		u.Z.	54	53	52	51	50	49	48	47	46	45	44	43	42	41	40	39	38	37	36	35	34	924
FW	16	FS	24	75	48	79	24	75	44	60	37	29	31	110	33	67	25	87	33	110	49	25	42	1107

	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	693
o.Z.	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	1827
u.Z.	33	32	31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	483
FS	32	28	110	23	41	54	92	29	32	54	55	30	99	22	39	35	51	57	32	22	110	1047
1107+1047 = 2170 = 70*31

a) 7, 21, 22 Zahlen

1. Das rechtwinklige Achsenkreuz ist eine Figur vollkommener Symmetrie. Ihm gegenüber hat das DR-Kreuz zwei weitere Eigenschaften:

· Die Doppelraute (DR) besitzt eine doppelte Symmetrie, indem von innen und von außen jeweils zwei Dreiecke zu einer Raute zusammenstoßen.

· Das DR-Kreuz enthält die Dimension der Fläche, die durch Faltung und Vereinigung der Außenpunkte zum dreidimensionalen Oktaeder geschlossen werden kann.

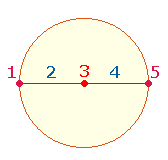
Vollkommene Symmetrie besteht in konzentrisch gleichen Maßen oder Zahlen, die von einem Mittelpunkt ausgehen oder auf ihn zulaufen. Jede Zahl kann einen Mittelpunkt für vorausgehende und nachfolgende Zahlen bilden. Die Zahl 55 ist jedoch von besonderer Bedeutung, da sie die Summe der Zahlen 1-10 ist und damit für das Dezimalsystem wesentlich ist.

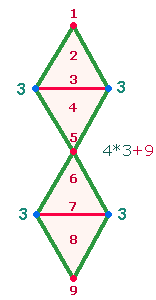
Von 55 aus ist die Summe konzentrischer Zahlenpaare jeweils 110 = 11*10. Dem Produkt 11*10 entsprechen in besonderer Weise die 21 Elemente der DR: 7 Punkte + 4 Dreiecksflächen und 2+8 Maßeinheiten (Linien). Die Gleichung 7*4 = 28 trifft auf die DR insofern zu, als ein einzelnes Dreieck aus 7 Elementen besteht. Durch zwei Rauten werden jeweils 3 Elemente, außerdem 1 Mittelpunkt eingespart, also insgesamt 7 Elemente.

Die konzentrischen Zahlenpaare sind gleichzeitig komplementär, indem die Grundzahlen von 1-9 die Zahl 5 als Mittelpunkt haben. Komplementäre Zahlen haben gleiche und sich gegenseitig ergänzende Bedeutung. Die gegenseitige Ergänzung komplementärer Zahlen besteht in besonderer Weise in der Addition ihrer Faktorenwerte (FW). Diese enthalten eine göttlich weise Ordnung, die zu unablässiger Ergründung antreiben und menschlicher Bemühung modellhafte Konstruktionen liefern kann, wie sich das von OVIDs Metamorphose Dädalus und Ikarus vermuten läßt.

Von 55 ausgehend sind die Primzahlen 13 und 97 die komplementäre Begrenzung von 85 Zahlen, die 42 Paare bilden. Von den addierten FW lassen sich wiederum FW ermitteln. Von dem alleinigen FW 16 der Zahl 55 ist kein weiterer FW zulässig.

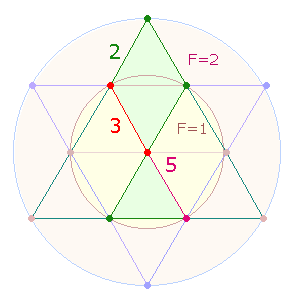
2. Im vorigen Kapitel wurden 43 Zahlen auf einem DR-Kreuz angeordnet. Um den gemeinsamen Mittelpunkt der einen DR auszugleichen, kann der zweiten DR, hier der horizontalen, zwei Mittelpunkte zugeteilt werden.

Nun fällt auf, daß von den 42 FS 7 doppelt, 1 dreifach und 1 vierfach vertreten sind:

2x	3x	4x
22 24 25 29 33 54 75	32	110

Auf diese Weise kommen 21 Zahlen zustande, mit der die 21 Elemente der DR besetzt werden können. 3 Längspunkte und 4 Querpunkte bilden das Punktemuster, das Ovid zur Kennzeichnung der Symmetrie eines Flügels benutzte:

Was konnte Ovid aus dem selektierten Punktemuster entnehmen und für seine Konstruktion übernehmen? Vermutlich mehr, als hier dargestellt werden kann und mir selbst bekannt ist:

· Die Einzelziffern von 32 und 110 weisen auf 3+2 Punkte des sanduhrförmigen Doppeldreiecks und auf 2 äußere Punkte hin. 3+2 ist auch auf 3+2 Radialelemente in der Bedeutung von 1:2 Kreisflächeneinheiten zu beziehen.

32 ist die 5. Potenz von 2 und gibt damit die 5 Punkte des hexagonalen und 2 Punkte des Erweiterungbereichs wieder, außerdem durch den FW 10 10 Linien der DR. 32+FW 10 = 42 = 2*21 läßt die Beziehung der Zahl 32 zum DR-Kreuz erkennen.

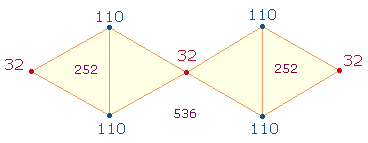
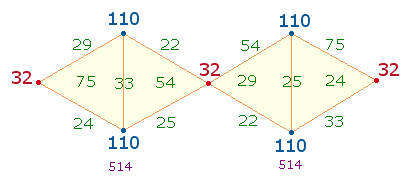
· Die Zahlen von 4*3 Dreieckspunkten (32+110+110) haben jeweils die Zahlensumme (ZS) 252 = 12*21. Summe und Faktoren zeigen Umkehrungen, denen spiegelsymmetrische Umkehrungen der vier Dreiecke entsprechen. Die Einzelziffern von 252 geben die Elemente der DR-Zickzacklinie wieder:

Der äußere Kreisring, der durch 2*2 Durchmesserelemente gekennzeichnet ist, hat die doppelte Fläche des inneren Kreises. Also gibt es von innen nach außen das Flächenverhältnis 1:2 und von außen nach innen das Flächenverhältnis 2:1.

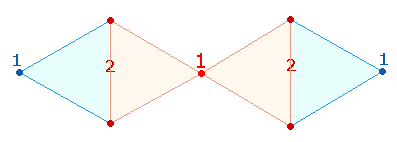
Die 7 DR-Punkte von einem äußeren Punkt aus gesehen sind in der Abfolge 1+2+1+2+1 angeordnet:

12:21 ist auch ein Verhältnis des Teils zum Ganzen in der DR:

4*3 = 12 "Dachelemente" + 9 Mittelelemente ergeben 21 Elemente.

· Die ZS einer Raute des Modells beträgt 252+32 = 284 = 4*71. Nun ist 71 der ZW 55 + FW 16. Die Einzelziffern bezeichnen 7 Rahmenelemente einer einzelnen Raute + ihren Mittelpunkt. 4*(7+1) Elemente machen ein DR-Kreuz aus.

· Auch OVID wählte 71 als ZS-Faktor der 13 A-Wörter: 639 = 9*71. Das 6. Wort AURA schließt mit der ZS 284 = 4*71 ab, sodaß 6:7 Wörtern das Verhältnis von 4:5 Durchmesserelementen entspricht.

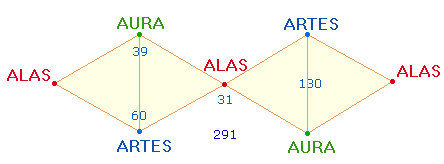
· Als deutliche Parallele zum vorliegenden Zahlenmodell weist OVIDs Konstruktion von 7 Wörtern auf den DR-Punkten das Prinzip der Umkehrung auf:

· ALAS mit der ZS 31 kehrt sich um in den Umkehrfaktor 13 der ZS 130 durch die ZS 99 von ARTES und AURA. Durch Hinzufügung des Mittelpunktwortes ALAS ist die Gesamtsumme 161 = 7*23 wiederum eine Umkehrzahl, und die Endsumme 291 = 3*97 erweist den Faktor 97 als Komplementärzahl zu 13. Bemerkenswert ist auch, daß die ZS 99 wie 220 der Vorlage durch 11 teilbar ist.

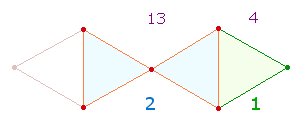
3. Die weiteren 14 Zahlen können nun in der Reihenfolge ihres Vorkommens eingetragen werden:

24 75 24 75 29 33 25 33 25 54 29 54 22 22

Die FS werden in den beiden Rauten spiegelsymmetrisch von außen nach innen eingetragen, der Beginn ist links unten mit der FS 24. Ab der zweiten Zahl (75) erfolgt die jeweils nächste Eintragung in derselben Raute. Auf diese Weise gibt es in einer Raute keine Doppelbesetzung mit derselben Zahl. Die Gesamtsumme ist 514+514+32 = 1060 = 20*53 >FW 62. 6:8 FS haben das Verhältnis 260:264 = 4*(65:66).

In einfacher Zählung ist die Summe von 8 zweistelligen Zahlen 294. Dies ist die FS der Zahlen von 1-30, die den 8 Zahlen – von der untersten zur obersten – zugeordnet werden können:

6	4	3	2	3	3	4	5	30
1 2 3 4 5 7	6 8 9 10	12 14 20	19 21	11 13 15	16 17 18	22 23 24 27	25 26 28 29 30	465
22	24	25	29	32	33	54	75	294
231+165 = 396						234+129 = 363		759
396:363 = 33*(12:11)

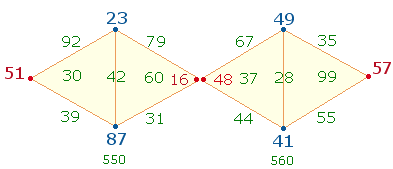
4. Die 22 Positionen der zweiten DR werden in der Reihenfolge ihres Auftretens von innen nach außen besetzt, diesmal mit jeweiligem spiegelsymmetrischen Wechsel:

16 48 79 44 60 37 31 67 87 49 42 28 23 41 92 55 30 99 39 35 51 57

Das Summenverhältnis der linken zur rechten Raute beträgt 550:560 = 10*(55:56) = 10*(111) = 1110. Die 3:3 Punktezahlen der äußeren Dreiecke (51 23 87; 41 49 57) haben das Verhältnis 161:147 = 7*(23:21) = 308, die Summe aller 8 Punkte 372 = 12*31.

5. Die beiden DR 1 und 2 mit 21 und 22 Positionen lassen sich in ihren Summen von zusammen 12 Binnenelementen und 7 Längspunkten vergleichen:

	DR 1	DR 2
6+6 BiE	240	296	536
3+4 LP	96	172	248
	336	468	804
536:248 = 268*(2:1) = 4*3*67
240:296 = 8*30:37); 336:468 = 12*(28:39)

Die Einzelziffern der Zahl 67 beziehen sich auf 6+7 Punkte des Tetraktyssterns und den beiden konzentrischen Kreisen: Die symmetrischen Elemente des äußeren Kreises zu denen des inneren Kreises sind doppelt so hoch und geben das Kreisflächenverhältnis 3:1 wieder, z.B. 12:6 Dreiecksflächen. 4*67 = 268 weist auf die Oktaederbildung durch ein DR-Kreuz mit vier Doppeldreiecken von jeweils 13 Elementen hin. Die FS 536 der 12 Binnenelemente ist gleich der Summe der 7 Punkte von DR 1.

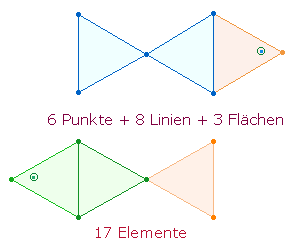
Die Summe der 8*3 Dachelemente beträgt 1366 = 2*683. Die Einzelziffern beziehen sich auf die 17 Elemente der "Fischfigur", die in der DR zweimal zu erkennen ist:

Die drei Dreiecke haben trinitarische Bedeutung. 683 ist weiterhin die FS der 6 Umkehrungen von 235:

Zahl	235	253	325	352	523	532	2220
FW	52	34	23	21	523	30	683

Die Zahlen (2+3)+5 geben 2*5 Radialelemente der beiden Tetraktyskreise wieder:

Die beiden DR eignen sich für ein DR-Kreuz. Wenn die Mittelpunktszahl 32 der DR 1 sich mit 514+560 zur Gesamtsumme 1106 verbindet, ergibt sich das Verhältnis 1106:1064: = 14*(79:76) = 14*155 = 2170.

6. Ohne den FW 16 der Mittelpunktszahl 55 betragen die FW der 42 FS 825 = 75*11. Die FW-Summen der vier Rauten sind:

	links	rechts
DR 1	145	155	300
DR 2	262	263	525
	407	418	825
300:525 = 75*(4:7)
407:418 = 11*(37:38)

Das Verhältnis 4:7 besteht nicht nur zwischen den Umkehrzahlen 12 und 21, sondern in der Summe aller 36 aufsteigenden und 36 absteigenden zweistelligen Umkehrzahlen. Das Verhältnis 407:418 eignet sich für eine Vereinigung der beiden DR zu einem DR-Kreuz. Die zweimal zwei Rauten der DR1 und DR2 folgen einem häufig auftretenden Prinzip: die FS 145 und 155 bilden ein Zahlenverhältnis 5*(29:31), die FS 262+263 sind angrenzende Konstitivzahlen für ihre Summe 525. 29 und 31 sind komplementäre Rahmenelemente zweier DR-Kreuze.

Die Summen der beiden DR und ihre FW sind 1060+300 = 1360 und 1110+525 = 1635, ihr Verhältnis 5*(272:327) = 5*599. Die Einzelziffern (5+9)+9 der Primzahl 599 sind als Durchmesserelemente der beiden Tetraktyskreise in der Bedeutung von (1+3)+3 = 7 Kreisflächeneinheiten zu verstehen.

Mit dem FW 16 beträgt die Gesamt-FS 841 = 29². Als sprechende Zahl bezeichnet 84+1 genau die 85 Zahlen von 13-97.

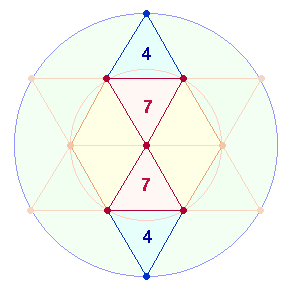
7. Die Trennung nach 21 sich wiederholenden und 21 einmaligen FS + 1 FW 16 erweist sich als sinnvoll auch in der Erweiterung um die übrigen 3 komplementären Zahlenpaare:

				6 Z.	85 Z.
o.Z.	98	99	100	297		sm
u.Z.	12	11	10	33
FS	23	28	21	72	2170	2242
FW	23	11	10	44	825	869
	34		21			3111
3111 = 3*17*61 >FW 81; 2242 = 2*19*59
869 = 79*11

Die Summen 23+28 = 51 sind bereits einmal vertreten und sind in verdoppelter Zahl hinzuzufügen: 25 Zahlen mit der FS 1060+102 = 1162, der FW-S 300+68 = 368. Von der FS 1110 und der FW-S 525 sind 23+28 = 51 bzw. 34 abzuziehen und einmaliges 21 bzw. 10 hinzuzufügen, die neuen Ergebnisse sind 1080 und 501. Es ergibt sich das Zahlenverhältnis 3*17*(30:31):

	Einzel-Z.	ZS	FW-S		Fkt.
DR 1	50	1162	368	1530	51*30
DR 2	41	1080	501	1581	51*31
	91	2242	869	3111

Es wurden einmal 85 und einmal 85+6 bzw 6+85 Zahlen betrachtet. In dreistelliger Zusammensetzung sind die Faktoren von 856 = 8*107 >FW 113 und 685 = 5*137 >FW 142. Die FW 113+142 = 255 ergeben 15*17 = 5*51, die FW 107+137 = 244 = 4*61. Die Einzelziffern der Zahl 3111 geben drei göttliche Personen als Kardinalzahl und als Einzelpersonen wieder. Die Umkehrzahl 1113 = 21*53 >FW 63 weist auf die Elemente der beiden geometrischen Figuren hin, aus denen der Oktaeder zusammensetzbar ist. Die FW der beiden Umkehrzahlen bilden das Verhältnis 81:63 = 9*(9:7) = 9*16 = 144. Weitere Ergebnisse sind hier zu finden.

b) 7 Zahlen, 7 Wörter

1. Wenn ein der Gematrie Kundiger sich an einem göttlich vollkommenen Zahlenmodell orientierte, war er überzeugt, daß Gott geradezu mit Vorbedacht für den Menschen Spielraum gelassen hatte, um an seiner Vollkommenheit ergänzend mitzuwirken. Diese Überzeugung kann als Bestandteil des Erwählungsbewußtseins Roms angesehen werden. Voraussetzung für solche ergänzenden Bemühungen ist eine innere Einsicht in das gewählte Modell. Nehmen wir zuversichtlich an, Ovid habe sich genau nach dem oben ausgeführten Modell der 7 Zahlen ausgerichtet, das ohne Wiederholungen nur aus zwei Zahlen besteht. Ovid verwendete drei verschiedene Wörter. Um Einblick in das von Ovid verwendete Modell zu erhalten, sind alle 4Werte zu ermitteln, zunächst nur für die drei Wörter und die entsprechenden drei Zahlen von links nach rechts:

	Modell				Ovid
ZS	110	110	110	330	31	39	60	130	460
FS	32	110	110	252	21	28	50	99	351
	142	220	220	582	52	67	110	229	811
FW1	18	18	18	54	31	16	12	59	113
FW2	10	18	18	46	10	11	12	33	79
	28	36	36	100	41	27	24	92	192
	170	256	256	682	93	94	134	321	1003
1003 = 59*17; 682 = 22*31 >44; 321 = 3*107 >110; 44:110 = 22*(5:2)
351 = 27*13 >22; 100:92 = 4*(25:23)

Die einander zugeordneten Positionen ergeben addiert folgende 4Werte:

	1 P	2 P
M	170	256	256	682
O	93	94	134	321
	263	350	390	1003

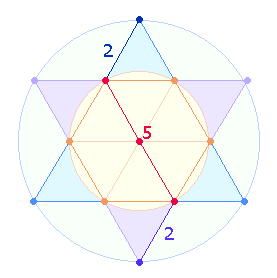
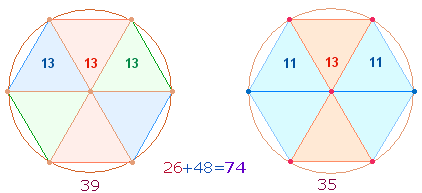
Das bedeutendsten Ergebnis sind die beiden Summen 350 und 390. 35 und 39 beziehen sich auf zwei Figurenkonstellationen des Hexagons:

Aus beiden Konstellationen können trinitarische Erkenntnisse gewonnen werden. Im SATOR-Quadrat entsprechen die Zahlen 26+48 einer einstelligen 1*1-Tabelle dem Wort AREPO:

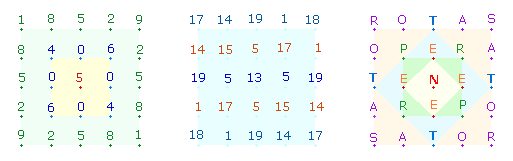
2. Der Mittelpunkt schließt die erste Raute ab. Die 4W-Summen sind nun:

	3 P	M P
M	682	170	852
O	321	93	414
	1003	263	1266
852 = 12*71; 414 = 18*23
1266 = 6*211 >FW 216

Der Faktor 211 stellt in der Aufteilung (2+1):1 das Kreisflächenverhältnis 3:1 der beiden Tetraktyskreise dar, 216 = 6³ die 6 Ecken des Oktaeders.

Es überrascht, daß die Faktoren 71 und 23, die in der einfachen Zählung der vier Rautenpunkte zustande kamen, sich in den 4W-Summen wiederholen:

	1 P	2 P	MP
M FS	32	220	32	284
O ZS	31	99	31	161
445 = 5*89 > 94				445
284 = 4*71; 161 = 7*23

Die Wiederholung beider Faktoren ist nicht durch ein gleiches rechnerisches Muster bedingt, sondern kommt unabhängig davon zustande. In der folgenden Tabelle entfällt die einfache Wertung:

		1 P	2 P	MP
M	(FS)	–	–	–
	FW2	10	36	10	56
	ZS	110	220	110	440
	FW1	18	36	18	72
128:440 = 8*(16:55)					568
O	(ZS)	–	–	–
	FW1	31	28	31	90
	FS	21	78	21	120
	FW2	10	23	10	43
	ZS	31	99	31	253
	253 = 11*23
GS	821+94 = 915 = 15*61 >69				821

Die FW der beiden Summenpaare 284+568, 161+253 sind 75+77 = 152, 30+34 = 64; 152:64 = 8*(19:8) = 8*27 = 216. Ein Grund für 71+23 = 94 könnte sein, daß wenn der Oktaeder die obere Ecke mit der unteren vertauscht, die Einzelziffern 9 und 4 durch den FW 49 erhalten bleiben. Der FW 69 und der Faktor 61 sind die ZS von SATOR TENET. 4 und 9 sind das Quadrat von 2 und 3, 8 und 27 die dritte Potenz.

Die 4W-Summen von 4+1 Punkten sind:

	6 P	1 P
M	1364	170	1534
O	642	93	735
	2006	263	2269
1364 = 44*31
1534 = 2*13*59

Vom 6. zum 7. Punkt gibt es im Zahlenmodell die Umkehrung von 31 zu 13. In Ovids ZS ist es der Wechsel der Komplementärzahlen 13 und 97: 260 = 20*13; 260+31 = 291 = 3*97.

3. Die 4W-Summen von 4+3 Punkten sind:

	4 P	3 P	7 P
M	852	682	1534
O	414	321	735
	1266	1003	2269
1534 = 2*13*59*
414 = 18*23 >31

Die Einzelziffern der Faktoren 13 und 59 geben die Entsprechung von 1:3 Kreisflächeneinheiten durch 5:9 Durchmesserelemente wieder, 414 die 9 Durchmesserelemente der DR.

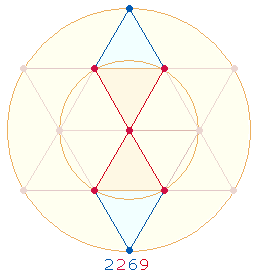
Die Primzahl 2269 stellt die Symmetrie der DR durch 2*2 Dreiecksflächen an den Anfang:

Die 15 Rahmenelemente der DR werden unterteilt in den hexagonalen und den Erweiterungsbereich.

c) Einzelberechnungen

1. Die Tabelle mit den 4Werten ermöglicht fast uferlose Einzelberechnungen:

· des Zahlen- und Wortmodells einzeln und beider zusammen

· eines der 4Werte oder mehrerer oder aller

· der ganzen DR und der Verbindung von zwei Einzelrauten und der DR (zwei Hälften und das Ganze)

· der Zusammenfassung von 3+4 Punktewerten.

Wieviele Berechnungen OVID selbst überprüft hat, können wir nicht wissen. Aber man möchte annehmen, daß wenn ein Berechnungsvergleich befriedigt, alle befriedigen.

Die Berechnungen erfolgen nach der sogenannten ZW/FW-Verrechnung.

2. Ich beginne mit der Zusammenfassung der 3 Längs- und 4 Querpunkte und lasse exemplarisch einige weitere Berechnungen folgen. Vollständigkeit ist nicht möglich. Das Zahlenmodell (M) geht Ovids Wortmodell (O) jeweils voran. Die erste Tabelle des Zahlenmodells verwendet die Ausgangswerte, die zweite die 4W-Summen:

M	3P	4P	sm	FW	sm	FW
FS	96	440	536	72	12:72 = 12*(1:6)
FW	13	22	35	12
sm			571	84	655	136
FW			571	14	585	24
sm					1240	160
655 = 5*131; 585 = 45*13 >24; 1240 = 40*31 >42

Die Ergebnisse sind geprägt durch Umkehrstruktur der 7 DR-Punkte. Die FW 13 und 22 haben eine doppelte Bedeutung:

· Aus 22 Elementen bestehen zwei Rauten mit je einem Mittelpunkt. 13 ist der FW von 22.

· Die Einzelziffern von 22 bezeichnen 2 Radialelemente und 2 Kreisflächeneinheiten, die Ziffern 1 und 3 1 hexagonale Kreisflächeneinheit und 3 Radialelemente. Es handelt sich um eine Definition, die erst nach Vollendung des Tetraktyssterns möglich ist und auf seinen hexagonalen Ursprung zurückweist.

M	3P	4P	sm	FW	sm	FW
4W-S	510	1024	1534	74
FW	27	20	47	47
sm			1581	121	1702	62
FW			51	22	73	73
sm			71*25		1775	135
FW					81	14
1581 = 3*17*31; 1702 = 46*37; 135 = 9*15

Die Einzelziffern der FW 74 und FW 47 weisen auf die Erweiterung des sanduhrförmigen Doppeldreiecks zu den Elementen zweier Rauten hin:

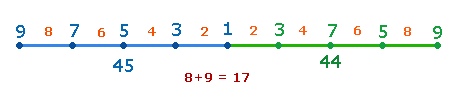
Die Zahl 135 bildet in den Verhältnissen 1:3 und 3:5 die Entsprechung von Kreisflächenverhältnis und Radialelementen ab und gibt dasselbe Flächenverhältnis durch das Produkt 5*27 und die FW 5+9 als Durchmesserelemente wieder. Sie stellt in dreistelliger Form die Punktenumerierung der Kreisachse dar:

Die drei Flächenebenen der Tetaktys bestehen aus 1+3+5 Flächen, die aufaddiert in dreistelliger Zusammensetzung die Zahl 149 ergibt, was die Summe 135+14 = 149 beweist:

3. Für Ovids DR wähle ich die 4W-Summen aus:

O	3P	4P	sm	FW	sm	FW
ZS	279	456	735	22
FW	37	28	65	18
sm			800	40	840	21
FW			20	11	31	31
sm						52

Die FW 31 und 21 wiederholen die ZS und FS des Wortes ALAS – Flügel. Den Einzelziffern entsprechen die beiden trinitarischen Kreisflächenverhältnissen 3:1 und 2:1. Die Einzelziffern der Summe 52 weisen auf 5+2 DR-Punkte in der Bedeutung von 1:2 Flächeneinheiten. Das Produkt 13*4 stellt die Erweiterung des sanduhrförmigen Doppeldreiecks zur "Fischfigur" mit 2:1 Dreiecksflächen dar:

ALAS hat also trinitarische Bedeutung: Der eine Gott in drei Personen hält seine "Flügel" schützend über seine Schöpfung. 52 ist die ZS von OPERA im SATOR-Quadrat. ALAS ist jedoch auch eine Verbform in der Bedeutung du mögest ernähren, fördern. In persönlicher Anrede bittet OVID den dreieinen Gott: ALAS ARTES AURA – Fördere die Künste durch deine Gunst. Das Wort AURA – Hauch, Luftzug hat auch die Bedeutung von Gunst.

d) Zwei Hälften und das Ganze

1. Für die Berechnung von zwei Hälften und des Ganzen wähle ich die 4W-Summen, zuerst einzeln das Zahlenmodell und Wortwahl Ovids, dann beide zusammen:

ZM	H.	H.	G.	sm	FW	sm	FW
	852	852	1534	3238	1621
FW	78	78	74	230	30
sm	1651 = 13*127			3468	1651	5119	5119
FW				41	140	181	181
3468 = 34*102 = 3*4*17² >21+20 = 41							5300

Das Endergebnis 5300 läßt sich aufteilen in 5+3 Radialelemente und 7+7 Punkte des Tetraktysstern mit einem zweiten Mittelpunkt. Beide geben das Kreisflächenverhältnis 3:1 wieder.

2. Für die DR Ovids ergibt sich:

O	H.	H.	G.	sm	FW	sm	FW
	414	414	735	1563	524
FW	31	31	22	84	14
sm	27*61			1647	538	2185	47
FW				70	271	341	42
2158 = 5*19*23 >47; 341 = 11*31; 538 = 2*269							89

Die Einzelziffern der drei FW geben das Kreisflächenverhältnis 1:(1+2) durch die Entsprechungen von Radialelementen und Flächeneinheiten.

Die Zahl 84 hat mehrere Bedeutungen. Drei davon sind:

· Das Produkt 7*12 kann aufgeteilt werden in (5+2)*(5+7) DR-Punkte in der Bedeutung von (1+2)+(1+3) = 3+4 Kreisflächeneinheiten.

· Die 4 Seiten eines Quadrats bestehen aus jeweils 2 Begrenzungspunkten und 1 Maßeinheit.

· Der Oktaeder hat einerseits eine quadratische Mittelbasis, andererseits besteht er aus 12 Kanten, jeweils 4 für die Pyramiden, zusammen 8, und 4 für die Mittelbasis.

89 ist die Komplementärzahl zu 21, in Einzelziffern zum Grundmaß von 2 Begrenzungspunkten und 1 Maßeinheit. Die reale Zahl 89 stellt eine Numerierungssumme von 5+4 Begrenzungspunkten und 4+4 Maßeinheiten vom Mittelpunkt aus dar:

Vom Mittelpunkt aus numeriert, bildet 89 die Hälfte eines Achsenkreuzes. Aus 8 Basis- + 9 pyramidalen Elementen besteht auch die Hälfte eines Oktaeders.

3. In Addition beider Modelle ergibt sich:

Die Verrechnung der Hälften und des Ganzen beider Modelle ergibt:

	ZM		O
	2 H.	G	2 H.	G	sm	FW	sm	FW
4WS	1704	1534	828	735	4801	4801
FW	156	74	62	22	314	159
sm					5115	4960
FW					50	46	96	13
4960:5115 = 5*31*(32:33); 96 = 4*(11+13)

Die Primzahl 4801 trennt 48 symmetrische Elemente des Tetraktyssterns von seinem Mittelpunkt. 314 bezieht sich als Gleichung 3+1 = 4 auf je 4 Punkte zweier Rauten in der DR:

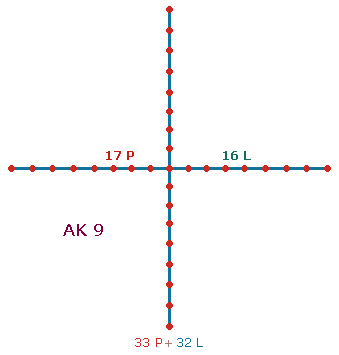
Das Verhältnis 32:33 entspricht den Elementen des Achsenkreuzes AK9:

Erstellt: März 2018

Inhalt II