26 Primzahlen von 1-100: 23+3 PZ nach Ordnungsmuster

Primzahlen 1-100

a) Primzahlmuster

1. Das grundlegende Primzahlmuster, das sich nach jeweils 30 Zahlen wiederholt, habe ich bereits vor Jahren dargelegt. Aus diesem Muster fallen die Primzahlen 2, 3 und 5 heraus. Zwischen 1 und 100 gibt es demnach 3+23 Primzahlen. Hier soll die Ordnung der 23 Primzahlen untersucht werden:

Primzahlen 1-100 nach Primzahlmuster

In horizontaler Ansicht besteht das Primzahlmuster 1-30 aus viermal je zwei Zahlen, deren Summen jeweils durch 12 teilbar sind und sich konzentrisch zweimal zu 60 ergänzen:

sm	12	36	24	48	120
/12	1	3	2	4	10

Mit jeder Wiederholung nach drei Zehnereinheiten wächst die Zahl um 8*30 = 240, sofern nicht eine oder mehrere Positionen von zusammengesetzten Zahlen besetzt sind. Demnach müßte die Summe der ersten drei Durchgänge (1-90) 120+360+600 = 1080 betragen. 49+77 = 126 sind jedoch abzuziehen, was 954 ergibt. Vom vierten Durchgang gehört nur die erste Zehnereinheit mit der Primzahl 97 zu 1-100.

2. Die 8 Primzahlen ergeben in konzentrischer Addition viermal jeweils 30:

1	7	11	13
29	23	19	17
30	30	30	30

3. Die Primzahlen 2, 3, 5 regulieren den Abstand zwischen den 8 Positionen des PZ-Musters, das in zwei Reihen im Abstand von jeweils 2*3 = 6 verläuft, wenn man die Zahl 5 als Ausgangszahl der zweiten Reihe nimmt:

1		7		13		19		(25)		40
	(5)		11		17		23		29	80

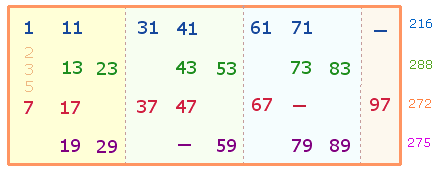
Zwei Zahlen mit gleicher Einerstelle gehören je einer Reihe an, z.B. 1 und 11, die Differenz ist jeweils 10, ihr Additionsergebnis 12. Nach regulärer Primzahlordnung treten Primzahlen mit derselben Einerziffer stets paarweise in zwei aufeinander folgenden Zehnereinheiten auf. Von 1-100 gibt es 10 solcher Primzahlpaare:

1	11	31	41	61	71	216
13	23	43	53	73	83	288
7	17	37	47			108
19	29	79	89			216
40	80	190	230	134	154	828
230:368:230 = 23(10:16:10) = 2336
432:396 = 36*(12:11)

Von 1-1000 sind es 51 Zahlenpaare, es verbleiben 67 Einzelprimzahlen mit dem Durchschnittswert 12*43 = 516. Näheres erfahren Sie in diesem Kapitel.

Die beiden Reihen treffen in ihren 6-er Abständen vermehrt auf zusammengesetzte Zahlen, z.B. 25.

b) Zwei Primzahlreihen

1. Die Wiederholung des Primzahlmusters begründet sich darin, daß die Zahl 3 erstmals nach 0 auftritt und nach 10 3-er Einheiten zum Ausgangspunkt (3)0 zurückkehrt. Die Positionen der beiden Primzahlreihen sind jeweils abwechselnd die 1. und 2. Zahl nach einer durch 3 teilbaren Zahl. Einer Primzahl der 1. Reihe geht – nach der ersten 3 – jeweils eine durch 2*3 teilbare Zahl (6, 12, 18) voraus, eine Primzahl der 2. Reihe überspringt die gerade Zahl nach der ersten 3 und setzt die Reihe in 6-er Schritten fort:

Reihe1		x						x						x						x						–
Pos.		1.						1.						1.						1.						1.
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Pos.						2.						2.						2.						2.						2.
Reihe2						x						x						x						x						x

Der Abstand zwischen der 1. Zahl nach Teilbarkeit durch 3 und der 2. Zahl nach folgender Teilbarkeit durch 3 ist 4 (1+5; 4+8). Die Addition der 1. und 2. Zahl ist daher immer durch 6 oder ein höheres Vielfaches von 6, z.B. 1+5 = 6, 11+13 = 24 teilbar.

2. Die Summe 1051 der 23 Primzahlen ist selbst eine Primzahl, wie auch 1061 unter Einschluß der drei Primzahlen 2, 3, 5.

Die ersten zwei horizontalen Reihen sind vollständig, genügen also der Zuwachsregel, also für die erste Reihe: 12+(12+60)+(12+120) = 216.

Die Ordnung der horizontalen Summen wird erkennbar, wenn man ihre Faktorenwerte (FW) ermittelt und sie dazuzählt:

	1	2	3	4
	216	288	272	275	1051
FW	15	16	25	21	77
	231	304	297	296	1128
1128 = 24*47
231:297 = 33*(7:9) = 528
304:296 = 8*(38:37) = 600

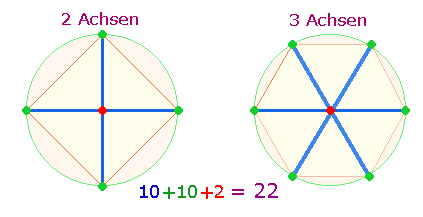
In den Gruppierungen 1+3 und 2+4 haben die Summen das Verhältnis 528:600 = 24*(22:25). Die Verhältniszahlen 22:25 betreffen den Doppelaspekt von zwei Figuren aus zwei und drei Achsen, die 4+6 = 10 Maßeinheiten des Dezimalsystems grundlegen und von 12 bzw. 15 Punkten (bei einem Mittelpunkt je Achse) begrenzt werden:

Zählt man für jede Achse einen Mittelpunkt, sind 3 Punkte mehr zu zählen:

ME	10	10	20
Pu.	12	15	27
	22	25	47

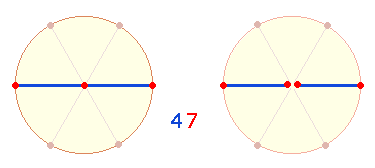
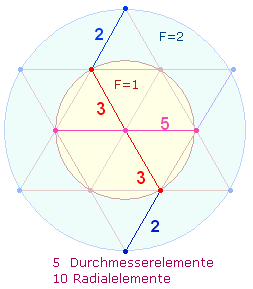
Auch die Zahl 47 selbst hat mit einem Doppelaspekt zu tun. Die Einzelziffern ihrer Konstitutivzahlen 23+24 sind auf 5 Durchmesser- und 2*3 Radialelemente der Kreisachse zu beziehen:

Die Zahl 47 bildet die Mitte der 21 Primzahlen von 11-97, deren Summe 1043 = 7*149 beträgt. Die Summe der ersten 11 Primzahlen ist 7*47, woraus sich das Verhältnis 7*(47:102) für 11:10 Primzahlen ergibt.

3. Die Summe 120 der 8 Primzahlen des ersten Primzahldurchgangs zeigt durch die Produktzahlen 10*12 die konkurrierenden Zählsysteme von 10-er und 12-er Einheiten, die im Tetraktysstern eine wesentliche Grundlage besitzen. 120 ist die Summe der Zahlen 1-15, 15 die Summe der Zahlen 1-5, die sowohl die Elemente der Kreisachse bilden als auch die Radialelemente einer Seite der Zickzacklinie der Doppelraute im Tetraktysstern:

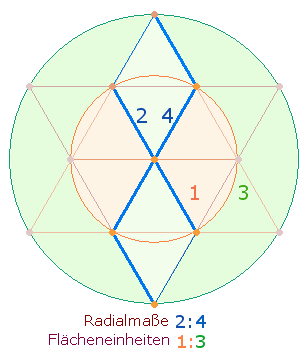
4. Das Flächenverhältnis der beiden konzentrischen Kreise des Tetraktyssterns beträgt 1:3. Die geometrischen Elemente des Hexagons und seiner Erweiterung sind in analoger Weise auf dieses Flächenverhältnis hingeordnet. So bedeuten etwa 2:4 Radialmaße der Doppelraute-Zickzacklinie das Flächenverhältnis 1:3.

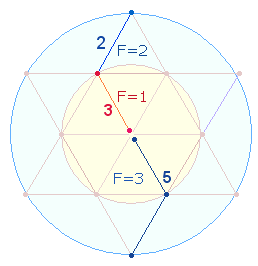
Die Primzahlen 2,3, 5 sind als Radialelemente der DR-Zickzacklinie anzusehen:

5 erweist sich als Summe von 3+2 Radialelementen und übernimmt als Ausgangszahl der zweiten Primzahlreihe eine Sonderaufgabe.

5. Das Primzahlmuster der in 6-er Abständen erfolgenden zwei Reihen kann endlos fortgesetzt werden. Es seien hier die ersten 4*8 Reihen dokumentiert, vertikal geordnet nach den Einerstellen 1, 3, 7, 9:

1.	1	31	61	151	244
	11	41	71	101	224	468	36*13
2.	13	43	73	103	232
	23	53	83	113	272	504	72*7
3.	7	37	67	97	208
	17	47	107	137	308	516	12*43
4.	19	79	109	139	346
	29	59	89	149	326	672	96*7
	120	390	660	990	2160

Jedes Zahlenpaar ist mindestens durch 6 teilbar, z.B. 67+107 = 174 = 6*29, häufiger durch 12 oder ein Mehrfaches von 6. Die Summen der 1. und 3. sowie 2. und 4. Doppelreihe sind durch 24 teilbar: 984:1176 = 24*(41:49), das Verhältnis der 2. zur 4. Doppelreihe 504:672 ist 7*24*(3:4) = 168*7.

Die ersten drei vertikalen Summen bilden mit der vierten das Verhältnis 1170:990 = 90*(13:11) = 90*24.

6. Die beiden Reihen verlaufen weder genau parallel noch halten sie Summengleichheit – mit einer staunenswerten Ausnahme: Mit der Zahl 5 besteht von 1-100 jede Reihe aus 12 Primzahlen und derselben Summe 528 = 48*11 = FW 11+11 = 22:

1	7	13	19	31	37	43	61	67	73	79	97	528
5	11	17	23	29	41	47	53	59	71	83	89	528

Die Einzelziffern der Summen 528 geben 7 Punkte und 8 Linien des DR-Rahmens wieder. Die beiden Summen sind also wieder auf die Bildung des Oktaeders ausgerichtet, der aus 4 Rauten mit je 11 Elementen zusammensetzbar ist. Dem entspricht die FW-Summe 44. Näheres dazu habe ich in einer früheren Untersuchung ausgeführt.

Die außergewöhnliche Summengleichheit der Primzahlen von 1-100 hat eine plausible Begründung in den 10+10 Punkten von zwei Tetraktys, und 100 ist 10*10.

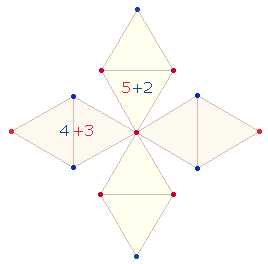
7. Auf die systemrelevante Bedeutung der Zahl 120 ist noch vertieft einzugehen. 120 ist aufteilbar in die Faktoren (3*4)*(2*5), die FW sind 7+7 = 14. Die Faktoren lassen sich als Punkte zweier DR in einem DR-Kreuz eintragen und zu einem Oktaeder zusammenfügen:

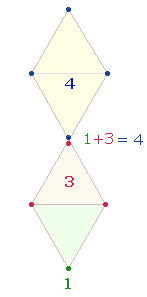
Die Ausrichtung der Zahl 120 auf das DR-Kreuz zeigt sich in der Hinzufügung ihres FW 14 und im Ergebnis 134, dessen Einzelziffern als Gleichung 1+3 = 4 die Punkte zweier Rauten wiedergeben:

134 ist Summe von 2*67, deren Einzelziffern als je 6 Binnenelemente und 7 Punkte einer DR verstanden werden können.

Erstellt: Juni, August 2019

Inhalt