HORAZ, CARMEN SAECULARE

Gematrische Gestaltung von 31 Götterbezeichnungen

Quadrat des Horaz und das SATOR-Quadrat

I. Das Quadrat des Horaz

II. Beide Quadrate

a) Überblick

b) SATOR CEREREM

c) Einzel- und Gesamtzählung von DR-Kreuz und Quadratrahmen

III. Die Initialen der 10 Wörter

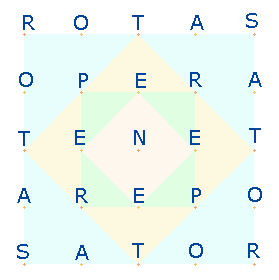
Zu den ehrgeizigen Zielen römischer Autoren gehört es, abgestimmt auf das SATOR-Quadrat (SQ) ein paralleles Buchstabenquadrat zu konstruieren. Wie es ihnen gelang, aus einem scheinbaren Gewirr von Buchstaben Ergebnisse von höchster Präzision zu erzielen, ist schwer zu begreifen.

Nach welchem Plan Horaz ein Buchstabenquadrat aus 5 Götterbezeichnungen und 26 Buchstaben entwickelte, habe ich im vorangehenden Kapitel darzulegen versucht. Es geht zunächst darum, die eigenständige Beschaffenheit des Quadrats zu betrachten, um dann das Buchstabenquadrat des Horaz und das SQ zusammen zu untersuchen:

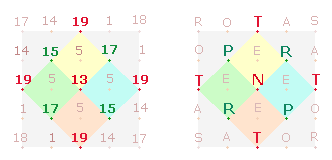
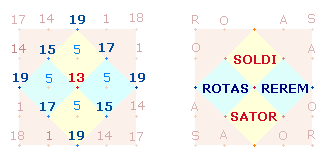
Die Zahlenentsprechungen der beiden Quadrate und ihre 4Werte sind auf einer eigenen Seite dokumentiert.

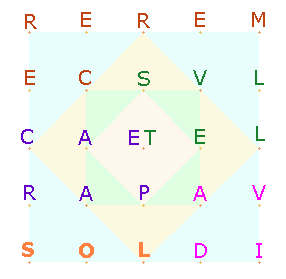
I. Das Quadrat des Horaz

1. Die ZS+FS der fünf Götterbezeichnungen SOL DIVA PARCAE TELLUS CEREREM beträgt 267+205 = 472 = 8*59. Die Bezeichnungen sind von unten links nach oben rechts in gewundenem Ablauf nach der Reihenfolge ihres Auftretens eingetragen. Der Mittelpunkt wird durch zwei Buchstaben (ET) besetzt, die nach ihrer Bedeutung "und" nicht nur die beiden Hälften miteinander verbinden, sondern auch die beiden Wörter:

	ZS	FS	sm
PARCAE	42	35	77
TELLUS	84	63	147
	126	98	224

TELLUS hat die doppelte ZS wie PARCAE, alle 4 Teilsummen sind durch 7 teilbar, das FS:ZS-Verhältnis ist 14*(7:9).

Die Zahl 224, zu verstehen als 2+24, bezieht sich auf den Oktaeder, der aus 3*8 Umlaufelementen und einer unteren und oberen Ecke besteht. Siehe dazu Dezimalmodell Oktaeder.

Die Namen PARCAE und TELLUS besetzen symmetrisch die Mitte des Quadrats. Die Buchstabenfolge ist demnach 7+12+7. Den 12 Buchstaben entspricht die Zahl der Kanten des Oktaeders.

Auch das SQ hat eine zentrierte ZS+FS 224 aufzuweisen. Auf das Verhältnis der beiden Summen wird in der Dokumentation der Zahlenwerte näher eingegangen

Das ZS+FS-Verhältnis der 2:3 Wörter beträgt 224:248 = 8*(28:31). Der gemeinsame Faktor 8 stützt die Vermutung, daß das Buchstabenquadrat in enger Beziehung zum Oktaeder konzipiert ist. Bezogen auf die 8 Flächen des Oktaeders ist die durchschnittliche ZS+FS 59.

2. Die ZS+FS der 5 Buchstabenzeilen – von unten nach oben – sind:

Zeile	1	2	3	4	5	sm
ZS	56	54	44	57	56	267
FS	38	36	44	36	51	205
sm	94	90	88	93	107	472
	184		88	200
8*(23:11:25) = 8*59

Die gematrischen Werte der einzelnen Zeilen stehen untereinander in ausgewogenem Verhältnis: Die ZS der ersten und fünften Zeile ist gleich, jeweils 56, zusammen 112, die Summe der zwei mittleren Zeilen beträgt 111. Das ZS-Verhältnis der 3 ungeraden Zeilen zu den 2 geraden ist 156:111 = 3*(52:37).

Die Primzahl 59 ist auch Faktor der ZS+FS 1003 = 17*59 der 12 angerufenen Götterbezeichnungen. Beide Wortgruppen zusammen haben somit die ZS+FS 59*(8+17). 8 verschiedene Buchstaben enthält das SQ mit der ZS 102, die übrigen 17 Buchstaben haben als ZS die Umkehrung 201. 102 und 201 sind die FS der Zahlen 1-16 und 1-23.

3. Fügt man zur ZS+FS 184 der untersten beiden Zeilen noch CA der Mittelzeile hinzu, ergeben sich folgende Summen der nun in 12+14 aufgeteilten Buchstaben:

Bu.	ZS	FS	sm
12	114	78	192
14	153	127	280
192:280 = 8*(24:35)
114:153 = 3*(38:51)
78:114 = 6*(13:19)
192=12*16; 280=14*20

Für die beiden Gruppen aus 12 und 14 Buchstaben ergeben sich die durchschnittliche ZW+FW 16 und 20, deren Buchstabenentsprechungen QU sind und sich – als Anfangsbuchstaben des Wortes QUADRATUM – auf den Quadratrahmen eines 5*5 Punkte Quadrats beziehen. Dieser besteht einerseits aus 8 Punkten + 8 Linien, andererseits zählt jede Quadratseite 5 Elemente, zusammen 20.

Die Buchstabenzahlen 12 und 14 bezeichnen 12 Kanten sowie 6 Ecken + 8 Flächen des Oktaeders, der eine quadratische Mittelbasis besitzt.

4. Die ZS+FS der 14 Buchstaben des (großen) Rautenquadrats beträgt 130+102 = 232, die der 12 äußeren Buchstaben 137+103 = 240. Das ZS+FS-Verhältnis ist demnach 8*(29:30).

5. Die 14 Buchstaben des Rautenquadrats (Rtqu) sind weiterhin so untergliedert: Die ZS der 4 Eckpunkte des Rtqu beträgt 42, die 2 Buchstaben ET im Zentrum haben den Umkehrwert 24, macht zusammen 66, die der 8 Buchstaben des inneren Quadratrahmens 64.

6. Hier soll bereits angemerkt werden, daß 64 die ZS von CEREREM ist und Horaz der Göttin CERES gewissermaßen dieses Buchstabenquadrat gewidmet hat. Denn im SQ ist die ZS 64, bestehend aus den 4 Eckbuchstaben des inneren Quadratrahmens, in die größere ZS 84 eingegliedert, der die ZS von TELLUS entspricht. Die Summe 84+64 = 148 = 4*37 wird im SQ bekanntlich dadurch erreicht, daß jede Quadratseite die ZS 37 hat.

148 beträgt indes auch die ZS 88+FS 60 des inneren Horaz-Quadrats (HQ) allein. Das ZS+FS-Verhältnis der 8+2 Buchstaben beträgt (64+36):(24+24) = 100:48 = 4*(25:12). Die Zahlen 25 und 12 stellen die 25 Elemente des Hexagons und 12 Erweiterungselemente der Tetraktys dar.

7. Die ZS+FS des äußeren Quadratrahmens beträgt 179+145 = 324, des inneren 64+36 = 100 und des Mittelpunktes 24+24 = 48. Das ZS+FS-Verhältnis des Mittelpunktes zum äußeren Quadratrahmen ist 12*(4:27) = 12*31 = 372. Das FS:ZS-Verhältnis des inneren Quadratrahmens ist 4*(9:16) und gibt damit die Punktezahl des inneren Quadrats und des äußeres Quadratrahmens wieder.

II. Beide Quadrate

Zunächst sollen die einfacheren, wenn auch nicht unbedeutenden Zusammenhänge beleuchtet werden, bevor das eigentliche Anliegen des Horaz untersucht wird.

a) Überblick

1. Die vereinten ZS+FS der beiden Quadrate sind, wieder von unten nach oben:

	ZS						FS
Zeile	1	2	3	4	5	sm	1	2	3	4	5	sm	GS
HQ	56	54	44	57	56	267	38	36	44	36	51	205	472
SQ	69	52	61	52	69	303	54	40	61	40	54	249	552
sm	125	106	105	109	125	570	92	76	105	76	105	454	1024
1024 = 32*32

Da jedes Buchstabenquadrat aus 16 Einzelquadraten besteht – die freilich nicht von Buchstaben besetzt sind – entfällt auf jedes von ihnen die ZS+FS 32.

Die ZS+FS jeder Zeile des SQ+HQ sind:

Zeile	1	2	3	4	5
ZS	125	106	105	109	125	570
FS	92	76	105	76	105	454
	217	182	210	185	230	1024

2. Faßt man die ZS 106+109 der geraden Zeilen 2 und 4 zusammen, enden vier Summen auf die Ziffer 5. Die ZS 105 der Mittelachse ist mit den asddierten übrigen 4 Summen jeweils durch 3*5 teilbar: 15*(7:31). Die Einzelziffern 3 und 5 sind auch in der ZS 125 erkennbar wegen der Potenz 5³, die den FW 15 ergibt.

3. Das herausragende Ergebnis der ZS beider Quadrate ist, daß den 12+12 Randbuchstaben der äußeren Quadratrahmen, also den Buchstaben außerhalb des Rautenquadrats, durch 130 (SQ) + 137 (HQ) die Gesamtsumme 267 des HQ entspricht und den 13+14 Buchstaben der Rautenquadrate die Gesamtsumme 303 (173+130) des SQ. Auffällig sind die Umkehrformen 137 und 173 bei zwei gleichbleibenden ZS 130.

4. Die ZS+FS der beiden äußeren Quadratrahmen und inneren Quadrate sind:

	äu. QR			inn. Qu.
	ZS	FS	sm	ZS	FS	sm
SQ	206	166	372	97	83	180
HQ	179	145	324	88	60	148
	385	311	696	185	143	328
372:324 = 12*(31:27); 180:148 = 4*(45:37)
385:185 = 5*(77:37); 696:328 = 8*(87:41)

Die ZS der inneren Quadratrahmen sind, wie bereits erwähnt, 84+64 = 148. Der Mittelpunkt besteht aus den Buchstaben NET mit der ZS 37, sodaß das Verhältnis der 3:16 Buchstaben 37*(1:4) beträgt.

5. Von Bedeutung ist das ZS+FS-Verhältnis beider Quadrate:

	ZS	FS	sm
SQ	303	249	552
HQ	267	205	472
552:472 = 8*(69:59)

Der gemeinsame Teiler ist am zutreffendsten wohl auf die 8 Flächen des Oktaeders zu beziehen. 69 ist die ZS des Wortes SATOR – Schöpfer, 59 kann dem Wort TRES – drei zugewiesen werden. Beide Wörter haben als Konsonanten die gleichen Buchstaben RST mit den zusammenhängenden ZW 17+18+19 = 54. Im trinitarischen Sinn bilden beide eine Ergänzung: Die ZS 69 des singularischen Wortes ist durch 3 teilbar, die ZS 59 der Pluralform TRES ist eine Primzahl.

Die komplementäre Bedeutung wird erkennbar aus den 4Werten beider Wörter:

	ZS	FS	sm	FW1	FW2	sm	GS
SATOR	69	54	123	26	11	37	160
TRES	59	49	108	59	14	73	181
	128	103	231	85	25	110	341
231:110 = 11*(21:10); 341=11*31

Die Zahl 231 ist die Summe der Zahlen 1-21 und entspricht damit einer Numerierung der 21 Elemente der Doppelraute (DR). Das Produkt 11*10 = 110 kann ergibt als Addition ebenfalls 21. 10 ist der FW der Zahl 21.

6. Durch eine gemischte Gruppierung von je 5 Wörtern ist ein höheres Zahlenverhältnis der ZS+FS möglich:

SQ	ZS	FS	sm	HQ	ZS	FS	sm
OPERA	52	40	92	SATOR	69	54	123
TENET	61	61	122	ROTAS	69	54	123
AREPO	52	40	92	DIVA	34	20	54
sm	165	141	306				300
TELLUS	84	63	147	SOL	43	28	71
CEREREM	64	59	123	PARCAE	42	35	77
sm			270				148
GS			476				448

In dieser Gruppierung bilden zweimal 5 Wörter das ZS+FS-Verhältnis

476:448 = 64*(9:7).

b) ROTAS CEREREM

1. In vorstehender Tabelle fällt die Gleichheit der ZS+FS 123 von CEREREM und ROTAS bzw. SATOR auf. Vertauscht sind lediglich die Einerziffern 9 und 4. Diese Gleichheit nutzt Horaz offenbar für seine eigentliche Konstruktion.

Die Gesamt-ZS+FS 32*32 scheint auf die ZS 64 von CEREREM abgestellt. Tatsächlich kann man die Buchstaben in zweimal 17+15 aufteilen, die als R und P die Eckpunkte des inneren Quadrats bilden:

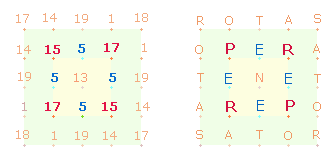
	C	M	R	E	E	E	R
ZW	3	12	17	5	5	5	17
ZS	15		17	15			17

Ebenfalls 32+32 beträgt die ZS von 4 Eckbuchstaben eines vierfach auftretenden kleinen Rautenquadrats:

Auch die ZW 19 und 13 lassen sich durch die Buchstaben von CEREREM bilden, jedoch unter Zuhilfenahme der FW, ohne daß die Rechnung ganz aufgeht. Wichtig ist hier lediglich die Potentialität der ZW-Bildung:

	C	E	M	R	E	E	C	R	E	R
ZW	3	5	12	17	5	5	–	–	–	17
FW	–	5	7	–	5	–	3	17	5	17
	13		19	17	15

Übrig bleiben 3+17+5+17 und 17, zusammen 59.

2. Den Mittelpunkt eines jeden kleinen Rautenquadrats bildet das E mit dem ZW 5, sodaß die Gesamt-ZS 64+5 = 69 beträgt, was der ZS von SATOR/ROTAS entspricht. CEREREM kann also durch die gemeinsame ZS+FS 123 mit einem Rautenquadrat identisch gesetzt werden.

3. Die 4 kleinen Rautenquadrate bilden horizontal und vertikal ein Achsenkreuz aus je zwei Rauten. Zählt man das N des Mittelpunktes für jede Raute, also zweimal je Achse, ist die ZS 2*69 = 138, läßt man ein N weg, beträgt die Summe 69+56 = 125. Die Ergänzung der Summe 56 leistet REREM als oberste Wortgruppe des Quadrats. Dieselbe ZS 56 hat auch die unterste Wortgruppe SOLDI. Die vier Rautenquadrate können etwa so (von unten nach oben, von links nach rechts) durch die vier Wörter ausgefüllt werden:

Der FW der Zahl 56 ist 13 und die Addition der beiden Werte ergibt 69, sodaß es aussehen kann, als handle es sich in einer Doppelraute zweimal um die Zahl 56, der nur in einem Fall ihr FW hinzugefügt wird.

Der FW von 69 ist 26. Die FW der beiden Zahlen 56 und 69 bilden somit das Verhältnis 13*(1:2). Die Zahl 13 wird in 31 umgekehrt durch die ZW/FW-Verrechnung:

			sm	FW
ZW	56	69	125	15
FW	13	26	39	16
sm				31

Die FW 15 und 16 bezeichnen die Rahmenelemente eine DR-Kreuzes, deren DR aus einem und zwei Mittelpunkten bestehen:

c) Einzel- und Gesamtzählung von DR-Kreuz und Quadratrahmen

1. In der folgenden Tabelle werden vom SQ und HQ die ZS und FS des DR-Kreuzes ermittelt, zuerst von jeder einzelnen Doppelraute, dann vom gesamten Rautenquadrat. Im ersteren Fall werden die Eckpunkte des inneren Quadrats und der Mittelpunkt doppelt gezählt:

	2 DR			Rautenqu.
	ZS	FS	sm	ZS	FS	sm	GS	GS	GS
SQ	250	222	472	173	159	332	423	381	804
HQ	179	140	319	130	102	232	309	242	551
	429	362	791	303	261	564	732	623	1355
791 = 7*113; 564 = 12*47; 232:319 = 29*(8:11)

Die ZS+FS 472 des Doppelrauten-Kreuzes des SQ ist auch die des ganzen HQ (267+205).

2. Angestrebt ist offensichtlich eine Zusammengehörigkeit von 4 Quadratseiten und einem DR-Kreuz aus 4 Rauten. Hinsichtlich der 4 Quadratseiten kann man ebenfalls zwei ZS+FS ermitteln: die jeder einzelnen Quadratseite und die des gesamten Quadratrahmens. Ich fasse die Summen zusammen und verweise für einzelne Werte auf die Dokumentation, ebenso auf die 4 Quadratseiten:

	ZS	FS	sm	ZS	FS	sm	GS	GS	GS
SQ	276	216	492	206	166	372	482	382	864
HQ	235	183	418	179	145	324	414	328	742
sm	511	399	910	385	311	696	896	710	1606

3. Die Gesamtsummen beider Quadrate betragen:

	einzeln			gesamt
	ZS	FS	sm	ZS	FS	sm	GS	GS	GS
innen	429	362	791	303	261	564	732	623	1355
außen	511	399	910	385	311	696	896	710	1606
sm	940	761	1701	688	572	1260	1628	1333	2961
1628 = 11*148 = FW 52; 1333 = 31*43 = FW 74; 52+74 = 126

Die Gesamt-ZS 1628 thematisiert ein weiteres Mal die Zahl 148, die ZS von CEREREM (64) und TELLUS (84).

Die Gesamtsumme des SQ beträgt 804+864 = 12*(67+72) = 12*139 = , die Gesamtsumme des HQ 551+742 = 1293 = 3*431. Die Summe der Faktoren 139+431 = 570 entspricht der ZS 303+267 der beiden Quadrate.

4. Das ZS+FS von gesamter zu einzelner Zählung beträgt 1260:1701= 63*(20:27) = 63*47. Die Einzelziffern der Zahlen 63 und 47 ergänzen sich komplementär zu 10. Beide Zahlen haben daher dieselbe Bedeutung. 47 ist die ZS von DEUS – Gott, für 63 steht die junge Wortprägung NUMEN – Gottheit zur Verfügung.

Zwei Summen sind durch 47 teilbar: Die ZS 940 der Einzelzählung von innen und außen und die ZS+FS 564 des Rautenquadrats beider Quadrate: 940+ 564 = 47*(20:12). Es kommt so das Gesamt-ZS+FS-Verhältnis 47*(32:31) zustande.

Die Zahl 63 ist mit 3 Doppelrauten zu je 21 Elementen in Verbindung zu bringen, 126 mit der Bildung von 3 Oktaedern aus 3*42 Elementen. Durch die Hinzufügung der FS 126 beträgt die Gesamtsumme 49*63. Hierbei bezeichnet 49 die Zahl der Elemente des Tetraktyssterns, die, um den FW 14 von 49 vermehrt, gleichzeitig die Elemente von 3 Doppelrauten ergeben.

5. Die Differenz zwischen gesamter und einzelner Zählung 7*63 = 21*21 beruht auf der Doppelzählung der Diagonalpunkte, im SQ 9, im HQ 10 Buchstaben, sie besitzt eine erstaunliche Binnenordnung. Zu unterscheiden ist der äußere Quadratrahmen (ä.QR) und das innere Quadrat (i.Qu.). Die rot gekennzeichneten Buchstaben sind keine Primzahlen und verantwortlich für die Differenz zwischen FS und ZS, es sind für jedes Quadrat vier Buchstaben:

	äu. QR				in. Qu.
		ZS	FS	sm		ZS	FS	sm	GS	GS	GS
SQ	SRSR	70	50	120	RPRP-N	77	63	140	147	113	260
HQ	SRMI	56	38	94	ACUA-ET	49	38	87	105	76	181
sm		126	88	214		126	101	227	252	189	441
189:252 = 63*(3:4)

Die 4 ZS sind jeweils durch 7 teilbar. Die Differenz zwischen FS und ZS beträgt im SQ 54 und im HQ 62 = 2*(27:31) = 116. Die Differenzverteilung der unteren zwei und oberen zwei Buchstabenzeilen ist 27+36 = 63 und 27+26 = 53.

Jedes Quadrat hat jeweils 4 weitere Buchstaben (re. Seite), deren ZW keine Primzahlen sind. Die ZS+FS der jeweils 8 Buchstaben sind gleich:

SQ	SSPP	66	32	98	OOOO	56	36	92	122	68	190
HQ	SMIU	59	30	89	OVPS	67	34	101	126	64	190
sm		125	62	187		123	70	193	248	132	380
132:248 = 4*(33:62)

III. Die Initialen der 10 Wörter

1. Die ZS+FS der 10 Wörter sind auf das Gesamtergebnis 1024 abgestimmt:

	ZS	FS	sm
SATOR	69	54	123
SDPTC	59	42	101
sm	128	96	224
96:128 = 32*(3:4)
224:800 = 32*(7:25)

Das ZS-Verhältnis 69:59 entspricht dem ZS+FS-Verhältnis der beiden Quadrate: 552:472 = 8*(69:59).

2. Auch die ZS der 4 Eckbuchstaben der beiden äußeren Quadratrahmen korrespondieren miteinander:

	ZS	FS	sm
SR-SR	35+35	50	120
SR-MI	35+21	38	94
sm	126	88	214
35:21 = 7*(5:3)
70:56 = 14*(5:4)

IV. Die 4Werte der beiden Quadrate

Erstellt: August 2011

Start

Inhalt