OVID METAMORPHOSEN

V. Weitere Beziehungen der 3 DR

a) Überblick

b) Die symmetrischen Elemente

c) Die Bedeutung der Zahl 148

d) 7 A-Verse

e) 7 MIN-Verse

f) Numerierung 1-23, 1-24

g) Gesamtsummen

h) 7+7 Wörter im DR-Kreuz und Oktaeder

a) Überblick

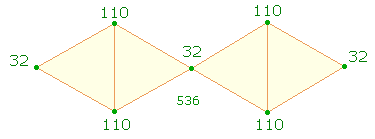
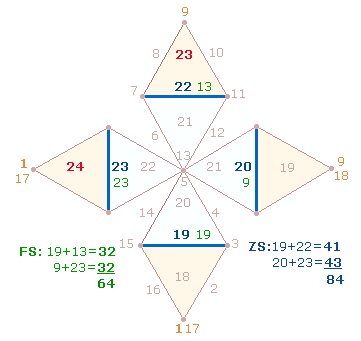
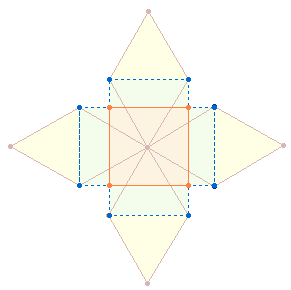
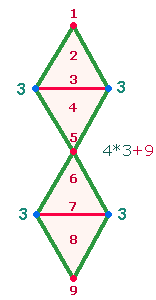
1. In dieser Fortsetzung des ersten Teils soll der Konzeption Ovids weiter auf den Grund gegangen werden. Die Doppelraute (DR) besteht aus vier gleichseitigen Dreiecken, die von einer Seite zur anderen jeweils spiegelsymmetrisch die Richtung wechseln oder umkehren. Die symmetrische Mitte verbindet zwei Rauten miteinander und demgemäß lassen sich die 7 Punkte als Umkehrmuster 3-1-3 darstellen.

Das Zahlenmodell der ersten Figur ergibt sich aus 42 komplementären Zahlenpaaren zwischen 13 und 97 und deren Faktorensummen (FS). Von letzteren passen 3+4 zum Punktemuster der DR. Die vorstehenden DR werden im folgenden von 1-3 numeriert.

13+97 = 110 bildet das erste von vier Zahlenpaaren, das aus zwei Primzahlen besteht. Die FS ist daher ebenfalls 110. Der Faktorenwert (FW) der ZS und FS ist jeweils 18, von 32 beträgt er 10. Diese 4Werte sind:

ZS	FS	sm	FW1	FW2	sm	GS
110	110	220	18	18	36	256
110	32	142	18	10	28	170
220	142	362	36	28	64	426
426 = 6*71 = FW 76

Die Zahl 71 ist Komplementärzahl zu 39, die in den Einzelziffern der Faktoren 3*13 die Punktestruktur der DR wiedergibt. Bemerkenswert ist die Umkehrung der Faktoren 17 und 71. Die ZS der 13 mit A beginnenden Wörter in Dädalus und Ikarus ist 639 = 9*71.

Die FS 32 ist dreimal in der DR vertreten, die 4W-Summe beträgt daher 510. Dies ist die ZS+FS der Dädalus-DR, die aus den Umkehrsummen 291+219 besteht.

2. Die 4W-Summen entsprechend dem Punktemuster 3-1-3 sind (426+256)+170+(426+256) = 682+170+682 = 1534 = 2*59*13 = FW 61+13 = 74. Die 4W-Summe von drei Punkten beträgt 682 = 22*31. Die Addition von 2*682 + 170 führt so zum Umkehrfaktor 13. Die ZS der Dädalus-DR gestaltet OVID so, daß sie sowohl die Umkehrfaktoren 13 und 31 als auch die Komplementärzahlen 13 und 97 enthält: 130+31+130 = 291 = 3*97.

Das Vorbild für die Zahl 97 konnte Ovid der ZS+FS der 3 Dreieckspunkte des Zahlenmodells entnehmen: 220+220+142 = 582 = 6*97.

3. Die Abstimmung der 3 DR ist im folgenden hauptsächlich an den ZS, den ZS+FS und an den 4W-Summen zu untersuchen.

b) Die symmetrischen Elemente

1. Als symmetrische Elemente sind hauptsächlich die 4 Querpunkte und jeweils 3 Punkte des linken und rechten Dreiecks anzusehen. Nachzuweisen ist, daß Ovid seine beiden DR auf dem Zahlenmodell aufbaute. Ich führe zunächst einen knappen und abgekürzten Beweisgang:

· Um die Symmetrie der 4 Querpunkte und der Dreieckspunkte zu überprüfen, sind die Mittelpunktwerte von der Gesamtsumme abzuziehen. Es werden die Summen der drei DR zusammengefaßt:

	GS	Abzug	Ergeb.
ZS	1517	210	1307
ZS+FS	2608	336	2272
4W-S	3457	497	2960
2272 = 32*71
2960 = 80*37

· Die 6 symmetrischen MIN-Wörter lassen keine gleichen gematrischen Hälften zu. Deshalb ist zunächst das Zahlenmodell nur mit den A-Wörtern zu kombinieren:

	GS	Abzug	Ergeb.
ZS	1061	141	920
ZS+FS	1816	194	1622
4W-S	2269	263	2006
1622 = 2*811
2006 = 2*17*59

Die Summenhälften sind an einem Längs- und zwei Querpunkten zu verdeutlichen:

	LP			2QP
	ZM	A-W.	sm	ZM	A-W.	sm	GS
ZS	31	110	141	220	99	319	460
ZS+FS	142	52	194	440	177	617	811
4W-S	170	93	263	512	228	740	1003

Das bedeutendste Ergebnis ist, daß die 4W-Summe 2*740 = 1480 der 4 Querpunkte die Hälfte der Gesamtsumme 2960 der 6 Punkte ausmacht. Ohne das Zahlenmodell wäre diese Gleichheit nicht vorhanden.

Die Summe 740 je zwei Querpunkte trifft sowohl vertikal als auch horizontal zu.

2. Zur Auffüllung der zweiten 4W-Summe 1480 durch die MIN-Wörter ist die Längspunktesumme 2*263 abzuziehen. Vom verbleibenden Rest 2*477 = 954 = 2*9*53 entfallen 149+150 = 299 auf die zwei Längspunkte und 655 auf die Querpunkte. Durch die beiden ungeraden Summen ist die Symmetrie der 3+3 Punkte verloren gegangen. Es ergibt sich für die Längspunkte (263+149)+(263+150) = 412+413 = 825 = 75*11 >24 und für die Querpunkte 1480+655 = 2135 = 35*61 >73, zusammen 2960. 825 ist die Summe der 42 FS des Zahlenmodells.

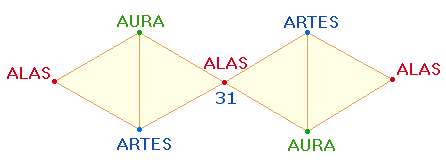
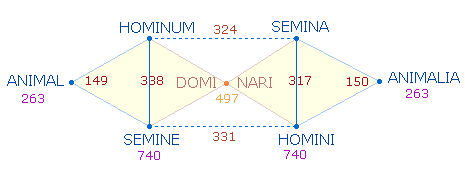
3. Ovid zielte offensichtlich in der Hinzufügung der MIN-Wörter auf keine völlige Symmetrie, sondern er wollte zu je einem Längspunkt und zwei Querpunkten sowohl vertikal als auch horizontal Zahlenverhältnisse erreichen. Die von ihm angestrebte Ordnung soll die folgende Grafik veranschaulichen:

Die violetten Zahlen geben die symmetrischen 4W-Summen des Zahlenmodells und der A-Wörter an. Zu den Konstanten 740+263 = 1003 = 17*59 sind die zwei 4W-Summen der MIN-Wörter hinzuzufügen:

li.	1003	338	149	1490	ob.	1003	324	149	1476
re.	1003	317	150	1470	unt.	1003	331	150	1484
	2006	655	299	2960		2006	655	299	2960
1476:1484 = 4*(371:369)

Die 4 ZS und FS sind:

					sm	FW
ZS	1490	1470	1476	1484	5920	52
FW	156	24	51	64	295	64
295 = 5*59; 52:64 = 4*(13:16)

Die Einzelziffern (5+5)+9 weisen auf 10 Radial- und 9 Durchmesserelemente der DR hin, 13+16 auf 29 Rahmenelemente des DR-Kreuzes. Die beiden Zahlen setzen sich zusammen aus 9+7 und den FW 6+7. 9 und 7 sind Komplementärzahlen zu 1 und 3 und haben trinitarische Bedeutung.

4. Die 4 Zahlenpaare sind in der Addition mit 740 durch 7 teilbar:

links	740	338	1078	7*154	oben	740	324	1064	7*152
rechts	740	317	1057	7*151	unten	740	331	1071	7*153
		655	2135				655	2135

					sm	FW
ZS	1078	1057	1064	1071	4270	70
FW	27	158	32	30	247	32
247 = 13*19

Die 4 Querpunkte bilden mit dem Mittelpunkt zwei Dreiecke. Die 4W-Summen der 5 Punkte sind durch 7 teilbar: 2135+497 = 2632 = 7*8*47.

c) Die Bedeutung der Zahl 148

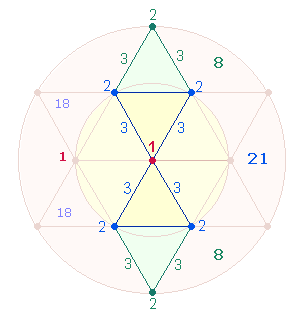
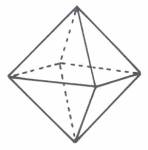
1. Die Querpunkte des DR-Kreuzes und die Querlinien bilden die quadratische Basis des Oktaeders. Die 7 MIN-Wörter bestehen aus 47 Buchstaben. Ovid folgt damit einem Numerierungsmodell von 1-23 und 1-24 eines DR-Kreuzes:

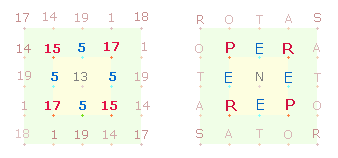
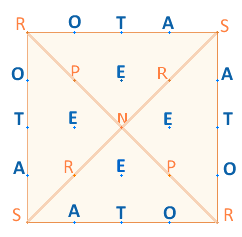
Die Querliniennummern der im Winkel stehenden Rauten sind 19+23 = 42 und 22+20 = 42, zusammen 84. Die entsprechenden FW sind 19+23 = 42 und 13+9 = 22, zusammen 64. Beide Summen ergeben 148 = 4*37. Dies ist auch die ZS der 4 Seiten des inneren Quadratrahmens des SATOR-Quadrats:

2. In einem innerem Sinnzusammenhang ergibt das Produkt der beiden Zahlen 19*23 die dreistellige Zusammensetzung 437. Die Einzelziffern bilden die Gleichung 4+3 = 7 und bezeichnen so die 2*7 Punkte des DR-Kreuzes.

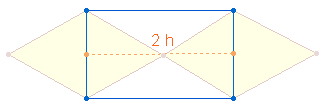
Die Zahl 437 kommt auf erstaunliche Weise auch durch die Rechteckfläche zustande, die durch die Querpunkte der DR gebildet wird:

Die Höhe zweier gleichseitiger Dreiecke beträgt Ö3 (Wurzel aus 3) = 1,732. Die Multiplikation der Bruchzahl mit 1000 ergibt 1732 = 4*433 = FW 437. Die zwei durch die Diagonalen gebildeten Dreiecke haben dieselbe Fläche wie die gleichseitigen Dreiecke. Ein Dreieck hat also im dreistelligen Bereich die Fläche 433. 4 Dreiecke einer DR oder stellvertretend 4 Querlinien für 8 Dreiecke des DR-Kreuzes haben demnach die Summe 1732. Die Summe der Einzelziffern weisen auf das Prinzip des Dezimalsystems hin. In der folgenden Grafik begrenzen 4+3+3 Punkte 3*3 Maßeinheiten:

Die Zahl 433 ist die 85. Primzahl und die symmetrische Mitte von 169 Primzahlen zwischen 1 und 1000.

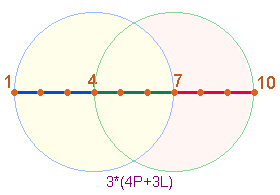
3. Im DR-Kreuz schneiden zwei Rechtecke ein Quadrat 1*1 aus:

Die 4 schmalen Rechtecke haben jeweils die Fläche (1732-1000)/2 = 366 = 6*61. 4*6*61 ergibt den FW 70 = 7*10 und den Bezug auf 7 hexagonale und 10 Tetraktyspunkte in der Bedeutung des Kreisflächenverhältnisses 1:3.

4. Die Zahlen 148 und 296 verbinden die beiden Ovid-DR:

· Die FS der 3 Längspunkte der MIN-Wörter ist 148:

	ZS	FW
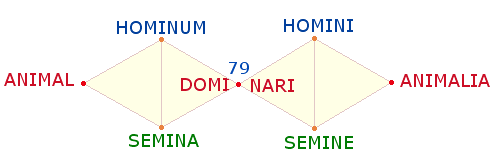
ANIMAL	47	39
DOMINARI	79	63
ANIMALIA	57	46
	193	148

· Die FW1/2-Summen der 4 Querpunkte der A- und MIN-Wörter sind 102+194 = 296.

d) 7 A-Verse

1. Ovid beläßt es nicht bei isolierten Berechnungen der 7 Wörter, sondern dokumentiert sie auch in den ZS+FS der 7 A-Verse. Einige Aspekte sollen näher betrachtet werden:

								sm
Vers	6	15	19	20	27	33	34	154
Wö.	7	7	7	7	6	5	8	47
	416	385	416	437	369	480	390	2893
FW	23	23	23	42	47	18	23	199
FS	330	287	303	287	289	338	282	2116
FW	21	48	104	48	34	28	52	335
2893 = 11*263 >274; 2116 = 4*23²

Die ZS 437 der symmetrischen Mitte bezieht sich, wie oben dargelegt, auf die 4 Querpunkte und Querlinien des DR-Kreuzes, die die Mittelbasis des Oktaeders bilden. Vers 20 lautet:

(geminas opifex libravit in alas)

ipse suum corpus MOTAQUE pependit in aura

(Der Baumeister schwang, das Gleichgewicht haltend, in die doppelten Flügel)

selbst seinen Körper und schwebte in der bewegten Luft.

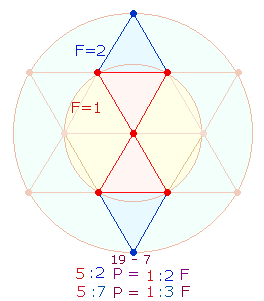
MOTAQUE bildet die symmetrische Mitte der 7 Wörter, auch die 35 Buchstaben sind symmetrisch geordnet im Verhältnis 14:7:14 = 7*(2:1:2), das die Verteilung der 7 DR-Punkte im Verhältnis 5:7 und dem Kreisflächenverhältnis 1:3 wiedergibt:

Das FS:ZS-Verhältnis von MOTAQUE ist 29*(2:3). Es läßt sich auf 2 Radialmaße und 3 Begrenzungspunkte der Kreisachse beziehen, das interne Differenzverhältnis 2:1 auf 2 Begrenzungspunkte und 1 Radialmaß der 3 Radialelemente. Die Buchstaben MO weisen durch ihre ZW 12+14 auf 26 Oktaederelemente hin, OTA ist Teil des Wortes SATOR mit der ZS 34.

Die 4Werte des Wortes sind:

	ZS	FS	sm	FW1	FW2	sm	GS
MOTAQUE	87	58	145	32	31	63	208
208 = 13*16

Den Faktoren der 4W-Summe entsprechen 13 Punkte und 16 Linien der Rahmenelemente eines DR-Kreuzes.

Die beiden Wortbestandteile MOTA und QUE haben die gleiche 4W-Summe und verdeutlichen so die Symmetrie des Flugapparates:

	ZS	FS	sm	FW1	FW2	sm	GS
MOTA	46	36	82	25	10	35	117
QUE	41	22	63	41	13	54	117

2. Der Faktor 263 dokumentiert die jeweilige 4W-Summe der zwei äußeren Längspunkte des Zahlenmodells und der A-Wörter (s.o.).

4 FW von ZS sind 23. Sie sind auf 4*5 Radialelemente eines DR-Rahmens beziehbar, ebenso wie die Faktoren 4*23² der FS 2116, deren Teilzahlen 21 und 16 die Numerierungssumme eines DR-Rahmens darstellen:

3. Auffällig sind zwei gleiche ZS 416 = 32*13 >23 und FS 287 = 7*41 >48. Ihre Summe ist 703 = 19*37 >FW 56 = 7*8. 19*37 verweist zweimal auf 10 Punkte der Tetraktys, 7*8 auf 15 Rahmenelemente der DR. Die FW-Summe 23+48 = 71 ist auf 7 DR-Punkte und zweitem Mittelpunkt beziehbar. Die Summe 703+71 = 774 = 2*387 = 18*43, ist als 7+8 Rahmenelemente der DR + 2+1 zusätzliche Elemente, wenn reihum numeriert und die 10. Position besetzt wird.

e) 7 MIN-Verse

1. Die 7 Verse haben folgende Werte:

								sm
Vers	1	2	3	6	9	10	13	44
Wö.	6	8	8	5	6	6	5	44
ZS	407	405	430	303	411	368	412	2736
FW	48	17	50	104	140	31	107	497
FS	282	317	301	269	331	254	295	2049
FW	52	317	50	269	331	129	64	1212
2736 = 144*19 = 6*456
303+269 = 572 = 4*11*13

Die ZS 2736 beträgt das Sechsfache der ZS der 7 MIN-Wörter.

497 hält die 4W-Summe des Mittelpunktes der 3 DR fest.

2. 303 ist die symmetrische Mitte der 7 Zeilen und ZS des SATOR-Quadrats (SQ). Die Zeile lautet:

sive recens tellus seductaque nuper ab alto

aethere cognati RETINEBAT semina caeli.

sei es, daß die junge Erde, die kurz zuvor getrennt worden war vom hohen

Äther, noch Samen des verwandten Himmels enthielt.

Die ZS+FS von RETINEBAT und MOTAQUE zeigt eine Gemeinsamkeit:

	ZS	FS	sm	FW1	FW2	sm	GS
RETINEBAT	90	87	177	13	32	45	222
MOTAQUE	87	58	145	32	31	63	208
	177	155	322				430
322 = 14*23 = FW 9+23 = 32

Die ZS 87 von MOTAQUE ist FS von RETINEBAT. Die rot hervorgehobenen Buchstaben der beiden Wörter sind im SQ enthalten. Die Buchstaben RETNEAT ergeben umgestellt das Wort RETENTA – das Zurückgehaltene. Die beiden Buchstabengruppen haben folgende Werte:

	ZS	FS	sm
RETENTA	79	79	158
OTAE	39	34	73
	118	113	231
231 = 21*11

Die 11 Buchstaben haben den durchschnittlichen ZW+FW 21. 231 ist die Summe der Zahlen 1-21 und hat somit Bezug zu den 21 Elementen der DR. Sie setzt sich auch aus der ZS des TENET-Kreuzes zusammen, wenn die Achsen einzeln und als ganzes Achsenkreuz gezählt werden: (61+61)+109 = 231.

Die Buchstaben OTAE können zu OETA umgestellt werden. Im östlichen Thessalien gibt es das OETA-Gebirge. Auf der höchsten Erhebung soll HERAKLES einen Scheiterhaufen errichtet und sich verbrannt haben. Durch Einzug zweier Diagonalen kann das SQ als eine Pyramide oder als Berg angesehen werden, wobei der äußere Quadratrahmen die Mittelbasis für zwei pyramidale Aufbauten steht:

Die 5 diagonalen Buchstaben können als Bergprofil und das innere Quadrat aus 9 Punkten als aufsteigendes Gelände gedeutet werden. Der Buchstabe N bildet auch in RETINEBAT die Symmetriemitte. 5 Diagonalbuchstaben einer Bergseite haben die ZS+FS 80+63 = 143 = 11*13, alle vier Seiten die ZS+FS 572, die ZS+FS des vierten Verses. Das ZS+FS-Verhältnis von 2:3 Wörtern der 4. Zeile ist (126+116):(177+153) = 242:330 = 22*(11:15) = 22*26. Aus 2*11 und 2*13 Elementen läßt sich der Oktaeder zusammensetzen. Ovid gestaltet die beiden Verse als gegenseitige Ergänzung, bei Dädalus und Ikarus liefert er den äußeren Quadratrahmen (437) und den Berg (OETA), bei der Erschaffung des Menschen die ZS+FS der diagonalen Dreiecke.

f) Numerierung 1-23, 1-24

1. Die ZS der beiden Mittelzeilen 437+303 = 740 = 5*148 wiederholt die 4W-Summe von zwei Querpunkte der zwei symmetrischen DR. Als Bezugspunkt wurde die Numerierung eines DR-Kreuzes von 1-23 und 1-24 genannt. Die beiden Numerierung liegen deshalb nahe, weil die FS der beiden Zahlenfolgen selbst die Umkehrzahlen 201+210 = 411 sind. Ovid macht 411 zur ZS des 4. MIN-Verses. Zwei weitere Summen weisen auf diese Numerierungen hin: die FS 269 und die FS 287+269 = 556 = 4*139. Der Faktor 139 tritt sowohl in der ZS+FS der 4 Querlinien + 8 Querpunkten auf als auch der 8 Dreiecksflächen (F) + 4 Querlinien, wenn die Werte der Querlinien zweimal gerechnet werden:

	QP	QL	sm	8 F	QL	sm	GS
ZS	72	84	156	168	84	252	408
FS	58	64	122	101	64	165	287
	130	148	278	269	148	417	695
278:417 = 139*(2:3) = 695

Die FS 287 und 269 der beiden mittleren Zeilen nimmt Ovid also aus dem Numerierungsbereich des DR-Kreuzes. Rechnet man die ZS+FS 148 nur einmal, erhält man 695-148 = 547. Die beiden Einzelsummen und die Gesamtsumme ergeben 278+417+547 = 1242 = 54*23. Auch die ZS der ersten drei Verse der MIN-Wörter ist 407+405+430 = 1242.

2. Die einmalige Zählung der FS 64 ergibt 287-64 = 223. Es ist offensichtlich, daß die Einzelziffern die 4 Querpunkte und 3 Längspunkte bezeichnen. Außerdem besteht eine Tetraktysseite aus 3 hexagonalen und 2*2 Erweiterungselementen.

3. Die Numerierungen sind auch deshalb so eindrucksvoll, weil die ZS+FS wiederum die Ausgangssumme 47
= 23+24 als Faktor enthält:

	1-23	1-24
ZS	276	300	576
FS	201	210	411
	477	510	987
987 = 21*47

987 ist auch die Komplementärzahl zu 123.

g) Gesamtsummen

1. Die ZS der 7+7 Verse ist 2736+2893 = 5629 = 13*433 = FW 446 = 2*223. Oben wurde bereits dargelegt, daß 433 die Fläche eine gleichseitigen Dreiecks ist. Der Faktor 13 könnte sich auf 9 Dreiecke der Tetraktys und 4 Dreiecke der DR beziehen. 223 wurde bereits oben als FS von 12 Binnenelementen und 8 Querpunkten der Numerierungen 1-23 und 1-24 ermittelt.

2. Die ZW/FW-Verrechnung der beiden FS ergibt:

			sm	FW
FS	2116	2049	4165	36
FW	50	686	736	33
sm				69
2049 = 3*683; 4165 = 5*7*7*17
736 = 23*32
2116 = 4*23²

69 ist die ZS des Wortes SATOR. 36 und 33 ist die ZS und FS der Zahlen 1-8. Der ZS 36 entsprechen die Buchstaben SAR, der FS 33 die Buchstaben TO. Die Zahl 8 ist auf 8 Flächen des Oktaeders zu beziehen.

3. Die Gesamt-ZS+FS beträgt 5629+4135 = 9794 = 2*59*83 = FW 144. Die Faktor 59 ist am ehesten auf 29+30 Rahmenelemente von zwei DR-Kreuzen zu beziehen, wobei eines einen Mittelpunkt und eines zwei Mittelpunkte hat. Dasselbe gilt für den Faktors 83 bei allen 41+42 Elementen.

h) 7+7 Wörter im DR-Kreuz

1. Zu unterscheiden sind wieder Querpunkte und Längspunkte, letztere aufgeteilt in Außenpunkte und Mittelpunkt:

	8 QP	4 AP	2 MP	sm
ZS	3264	1625	740	5629
FS	2420	1189	556	4165
	5684	2814	1296	9794
3264 = 32*102; 2814 = 14*201
5684 = 28*203 >47; 1296 = 12*108
1625 = 125*13 >28; 2420 = 220*11 >31
1189 = 29*41

Die DR ist geprägt durch die Zahlen 1+2/2+1 und 2+3/3+2: Die Zahlen 2 und 3 werden erkennbar an der einzelnen DR-Zickzacklinie als hexagonale Durchmesserelemente und als zweimal 5 Radialelemente, die Zahlen 1 und 2 an einer Querlinie + zwei Flächen sowie einem Querlinienpunkt + zwei Linien:

Die Aufteilung in 12 "Dachelemente" und 9 Vertikalelemente begründen die zweistelliger Zusammensetzung die Umkehrungen 69 und 96. Im Oktaeder werden 2+3 und 3+2 Elemente zum wesentlichen Bauprinzip: Vom unteren Ecke bis zu oberen und von der oberen zur unteren sind es je 5 Elemente. Die Ecken werden dabei jeweils doppelt gezählt, vergleichbar mit den Radialelementen. Der ganze Oktaeder wird durch 4*(5+5) oder 8*(2+3) bzw. 8*(3+2) Elemente erfaßt:

Zählt man die Oktaederelemente in ihrem ganzen Umlauf, so ergeben sich vertikal 4*8 Elemente, indem von der untersten zu obersten Ecke 3+2 bzw. 2+3 Elemente und auf der anderen Seite ohne beide Ecken 2+1/1+2 Elemente gezählt werden. Horizontal sind 3 Umläufe mit 24 Elementen zu zählen, beginnend von einer unteren und oberen Kante und einem Punkt der Mittelbasis. Auf diese Weise kommen 7*8 = 56 Elemente zustande. Unberücksichtigt bleiben bei der horizontalen Zählung die untere und obere Ecke, die zu 24 oder 56 hinzugefügt werden können.

5+5 und 5+3 für einen Oktaederumlauf bildet eine Doppelzählung, die in zweistelliger Zusammensetzung 108 = 9*12 ergibt. Hier ist eine der Bedeutungen der Zahl 108 zu finden. Die ZS+FS des Mittelpunktes ist 12*108 (s.o.).

Ovid hat den Zusammenhang von 7*8 Umläufen durch 4 doppelte Summen dargestellt:

FS	282	287	303	287	282	1441	11*131 >142
FW	52	48	104	48	52		304
ZS	416	416	303			1135	5*227 >232
FW	23	23	104				150
2576 = 7*8*23						2576	454 = 2*227

282 = 6*47 > 52 und 303 = 3*101 >104 stammen aus den MIN-Versen. Das FS:ZS-Verhältnis ist 156:585 = 3*13*(4:15). 585 ist 45*13 >24, die übrige Summe 1991 = 181*11 >192. Das Verhältnis 24:192 ist 24*(1:8) = 216 = 6³, Kennzeichen für die 6 Punkte und Dreidimensionalität des Oktaeders.

216 ergibt sich auch aus der ZW/FW-Verrechnung der Zahlen 55 und 53:

			sm	FW	sm	FW
ZS	55	53	108	13
FW	16	53	69	26
sm			177	39	216	15
FW			62	16	78	18
sm						33

56 ist auch zweimal die Summe der Zahlen 1-7, sodaß ein DR-Kreuz aus zweimal 7 Punkten besonders geeignet erscheint. Die Produktzahlen 7*8 stimmen auch mit 7 Punkten und 8 Linien des DR-Rahmens überein.

2. Auffällig ist zweimal die FS 227. Ihre Konstitutivzahlen 113 >113 und 114 >24 geben jeweils 2 Radialmaße, einmal 3 Durchmesserpunkte und einmal 4 Radialpunkte:

In der DR sind die Radialmaße durch Dreiecksflächen vertreten, die Durchmesserpunkte durch die Längspunkte und die Radialpunkte durch die Querpunkte. 2*227 stellt ein DR-Kreuz dar, das zu einem Oktaeder aus 6 Ecken und 8 Flächen wird.

Die FS 137 ergibt mit ihren beiden Konstitutivzahlen 113+114 zusammen 364, die ZS von SATOR OPERA TENET – TENET OPERA ROTAS des SATOR-Quadrats. Auch beim SQ ist die Mittelzeile zweimal zu lesen. ZS und FS sind Primzahlen und lassen sich nicht weiter verwerten, sie haben absolute Geltung.

Welch großen Wert Ovid auf die Zahl 227 gelegt hat, zeigt die Verwertung der ZS+FS der 2+4 Oktaederpunkte (s.u.):

	2 LP	4 P	sm	FW	sm	FW
ZS+FS	4110	5684	9794	144
FW	147	47	194	99	13*787
sm	44*227		9988	243	10231	800
FW			242	15	257	257
sm	1057 = 7*151					1057

242 kann, wie oben dargelegt, als 24+2 horizontale Oktaeder gelesen werden. In der Aufteilung 2*(11*11) läßt sich ein Oktaeder zusammensetzen. 257 und 7*151 bilden in ihren Einzelziffern eine Gleichung von je 7 DR-Punkten: 2+5 = 7 und 7 = 1+5+1.

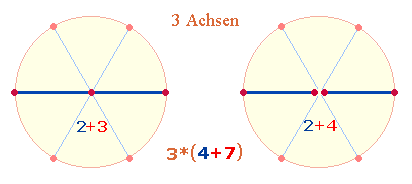
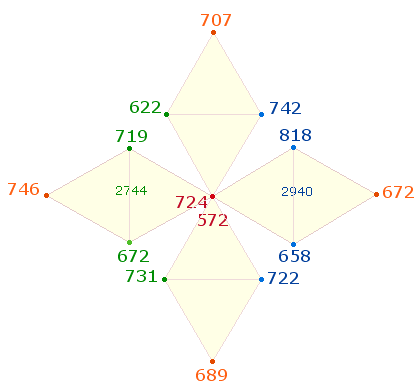
3. Obwohl ZS und FS allein sinnvolle Ordnungen bilden, sollen sie hier addiert behandelt werden. ZS+FS werden also auf den Punkten eines DR-Kreuz angeordnet, die 7 MIN-Verse auf der vertikalen, die 7 A-Verse auf der horizontalen DR:

Bei der Oktaederbildung bilden je zwei Querpunkte benachbarter Rauten eine Punkt der Mittelbasis. Die beiden Seiten sind hier grün und blau unterschieden. Das ZS-Verhältnis 2744:2940 = 14²*(15:14) läßt keinen Zufall zu. Ovid mußte zuerst festlegen, welche Verse die vertikale und welche die horizontale DR bilden, sodann in der Reihenfolge der Verse die Positionen der 8 Verse genau bestimmen, damit sie im DR-Kreuz in der passenden Weise zueinander standen:

Rf.	1	2	3	4	5	6	7	28
MIN	689	722	731	572	742	622	707	4785
Rf.	1	2	3	4	5	6	7	28
A	746	672	719	724	658	818	672	5009

Die Summe der Positionen für die grünen Werte sind (3+6)+(2+3) = 9+5 = 14, für die blauen (2+5)+(5+6) = 7+11 = 18, = 2*(7:9), zusammen 32. Die Summe für die übrigen Punkte ist 24. Die beiden Summen entsprechen den 4*8 und 3*8 Umlaufelementen des Oktaeders.

Der gemeinsame Teiler 14² ist zu verstehen als 2*(8+6) = zweimal 8 Rahmenlinien + 6 Punkte des DR-Kreuzes, nachdem bei der Vereinigung der Außenpunkte (AP) jeweils der 7. Punkt entfallen ist.

4. Die ZS+FS der 6 Oktaederpunkte und ihre FW sind:

	ZS+FS					FW		sm	FW	sm
2QP	1341	1560	2901	MP	1296	155	27	182	20
2QP	1403	1380	2783	AP	2814	84	35	119	79
sm	2744	2940	5684		4110	239	62	301	99	400
1403:1380 = 23*(61:60) >23+22 = 45; 4110+99 = 4209 = 3*61*23
1560:1380 = 60*(26:23); 182:119 = 7*(26:17)

Die FW-Summe 400 = 20*20 verweist wiederum auf die Oktaederbildung mit Einsparung des 7. Punktes, sodaß eine DR aus 20 Elementen besteht.

3 QP-Summen bilden Zahlenverhältnisse untereinander. Ihre Summe 4343 sind als je 4 Querpunkte und 3 Längspunkte eines DR-Kreuzes zu verstehen.

Die Summe 4110 des Mittelpunktes + der FW-Summe 99 stellt durch den Faktor 23 eine Verbindung zu den 4 Querpunkten her.

Die Einzelziffern der Produkte 23*61 sind auf die DR mit 5 hexagonalen Punkten und 7 Gesamtpunkten zu beziehen mit der Kreisflächenentsprechung 1:3.

Erstellt: April 2018

Inhalt II