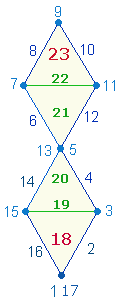
Das SATOR-Quadrat und die Quadratform des
Einmaleins
A. Das Prinzip des Außen und Innen
I. Einleitung
II. Die Zahlenfolge von außen und innen
III. Die Struktur des Einmaleins-Quadrats
IV. Die einstellige 1x1-Tabelle und das
SATOR-Quadrat
V. Die Dreifachzählung
des SATOR-Quadrats
B. Beziehungen zwischen dem einstelligen 5x5-Quadrat und dem
SATOR-Quadrat
I.
Einleitung
1. Die
folgenden Ausführungen nehmen ihren Ausgang von dem Beitrag Palindrome;
Struktur des SATOR-Quadrats.
2. Das
SATOR-Quadrat (SQ) ist das Ergebnis eines kühnen Unterfangens, lateinische
Buchstaben, Wörter und Sprache in Einklang mit dem Dezimalsystem und den Zahlenstrukturen
geometrischer
Figuren
zu bringen. Die Zahlenfolge des Dezimalsystem besitzt ihre vielfältigen eigenen
Strukturen. Im Einmaleins ist es zu einer quadratischen Figur ausgeformt. Im ersten Teil, der sich mit der
Definition von Palindromen beschäftigte, zeigte sich eine doppelte Leseweise
des SQ, von außen und von
innen.
Es geht
um die Frage, wie sich das Außen zum Innen und das Innen zum Außen verhält.
Alles Leben wird durch einen inneren Plan gesteuert. Das Computerzeitalter
kennt dafür zwei erhellende Begriffe, CPU (Central Processing Unit) und
Peripheriegeräte oder Ausgabegeräte, z.B. Bildschirm und Drucker.
3. Die
Römer hatten ursprünglich keine anthropomorphen Gottesvorstellungen. Nach ihrer
Auffassung wurde alles Leben in der Natur durch göttliche Kräfte bestimmt, die jedem
Lebewesen seinen inneren Plan geben. Das Wort für die Wirkkraft alles Lebendigen ist VIS. Auch im Zusammenhang mit abstrakten Begriffen und Ideen
wird VIS im
Sinne von Wesen, Beschaffenheit, Bedeutung verwendet. Der innere Plan eines Lebewesens ist
gleichzeitig sein Gesetz. Dieser Zusammenhang erscheint in der
Buchstabenumstellung VIS – IUS – Recht. Der Begriff Recht hat gewiß mehrfache Bedeutung, aber
menschliche Rechtssetzung findet ihren Maßstab im Gesetz der menschlichen
Natur.
4. Das SQ hat die regelmäßige
Form eines 5*5 Punkte Quadrat. Es kann kein Zweifel bestehen, daß
die Bedeutungsstrukturen dieser Quadratform gründlich erforscht wurden, bevor
die Idee entstand, Zahlen und Buchstaben miteinander zu verbinden . Die Annahme
eines Mathematikers, die 1x1-Tabelle habe dem SQ als eigentliches Modell gedient, hat viel Wahrscheinlichkeit
für sich.
Man muß
sich also dem SQ von zwei Seiten nähern, von der linearen Zahlenfolge des
Dezimalsystems und von den geometrischen Figuren, allen voran dem Kreis mit seinen
verschiedenen Einteilungsformen.
II. Die Zahlenfolge von außen und innen
1. Betrachtet
man die Zahl 1 für sich als Beginn einer kontinuierlichen Zahlenfolge, so wird
man unter einem philosophischen Blickwinkel sagen, die Zahl 1 sei der Ursprung
aller weiteren Zahlen. Die Zahl hat eine doppelte Bedeutung: Man kann Vorhandenes abzählen
unter dem Gesichtspunkt von Zählbarem. Die zweite Bedeutung ist, daß etwas
Meßbares nach bestimmten Maßeinheiten gezählt oder berechnet wird. Wenn es um
eine unbekannte Längenerstreckung geht, wird man Anfang und Ende durch Punkte
markieren, um die Zahl der Maßeinheiten oder die Mitte zu bestimmen. Soll um
die Mitte ein Kreis geschlagen werden, wird der Mittelpunkt zum Anfang und die
Peripherie zum Ende.
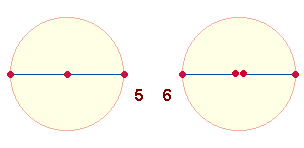
Natürlich
kann auch der umgekehrte Weg der Kreisbildung beschritten werden: Man legt ein
Maß fest, das sich um den Mittelpunkt in gleichem Abstand dreht. Das Maß des
Kreises ist an einer durch den Mittelpunkt des Kreises zu ziehenden Linie
ablesbar. Diese Linie schneidet den Kreisbogen in zwei Punkten. Man zählt somit
3 Punkte und 2 Radiallinien.
Die Kreiskonstruktion
mit Durchmesser (DM)-Linie ist das Grundmodell für ungerade und gerade Zahlen. Denn zwei gleichberechtigte Radien
bestehen aus 1 Linie und 2 Begrenzungspunkten, somit können den 5 Durchmesserelementen 2*3 = 6 Radialelemente zur
Seite gestellt werden:
|
|
2.
Die Betrachtungsweise gerader Radialelemente
ist für die Zahl 10 als nächsthöhere Zahleneinheit nach 5 relevant. Geometrisch
erhält man diese Zahl, wenn man dem Radialmaß des einfachen Kreises ein
weiteres hinzufügt, sodaß sich 2*5 Radialelemente ergeben. Die Zahl der DM-Elemente ist 9, die Grundlage des 1x1-Schemas.
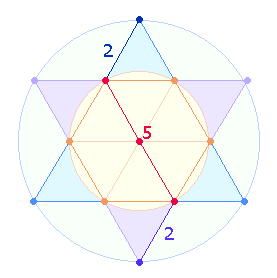
Das geometrische
Modell für die Zahl 9 ist insbesondere der Tetraktysstern:
|
|
3.
Die Zahl 10 ist also zu verstehen als eine Einheit aus 9 DM-Elementen und
einem weiteren Radialmittelpunkt, der eine höhere Zahlenstufe auf der Basis 1 bildet. Mit ihr wird
die Zahlenfolge 1-9 zur nächst höheren Zahleneinheit mit dem Index 1 (römisch =
X) zusammengefaßt.
III. Die Struktur des Einmaleins-Quadrats
a) Aufbau des
Quadrats
a)
Aufbau des Quadrats
1. Einmaleinstabellen
gab es bereits bei den Babyloniern vor 4000 Jahren, und bei den Griechen und
Römern. Was regt den menschlichen Geist an, solche Rechnungen durchzuführen?
Wenn man sagt dreimal zwei, dann handelt es sich bei der Zahl zwei um etwas
Zusammengehöriges, das dreimal vorhanden ist.
Ein
weiterer wichtiger mathematischer Grund dürfte sein, daß durch die
Multiplikation zweier Zahlen ein Flächenmaß bezeichnet wird.
2. Unter
dem Einmaleins versteht man gewöhnlich die Multiplikation der Zahlen 1-9, indem fortschreitend
jede Zahl mit jeder multipliziert wird. Eine systematische Darstellungsform
bietet sich von selbst an. Nach römischer Gewohnheit werden Zahlenreihen von
unten nach oben geschrieben, sodaß die oberste Stelle, die "summa",
das Additionsergebnis darstellt. Beginnt man also die Multiplikationsreihen von
unten links, so kann dies horizontal und vertikal geschehen:
|
|
10 |
|
|
|
|
|
|
|
90 |
|
|
|
9 |
|
|
|
|
|
|
|
1 |
90 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
|
|
|
|
|
Die
Darstellbarkeit in zwei Richtungen gibt bereits die Grundvorstellung einer
quadratischen Form. Zählt man die Positionen von 1-9 nach beiden Richtungen, ist das
Ergebnis 2*9
= 18 (2 Symmetriemittelpunkte), zählt man von einem
Ende 9 durch bis zum andern
Ende 9 (1
Symmetriemittelpunkt), ist das Ergebnis 17. Damit erhält man die
Eckbuchstaben S und R des SQ. (Im SQ sind zu den
Punkten die Linien je Quadratseiten hinzuzuzählen!)
Die Zahl 1 ist spiegelsymmetrischer Mittelpunkt für die
im rechten Winkel nach zwei Richtungen verlaufenden Zahlenreihe. Von einem
äußeren Ende bis zum anderen gelesen handelt es sich um ein Palindrom 9-1-9.
Die Zahl
5 ist die Symmetriemitte beider Reihen, 4 symmetrische
Zahlenpaare ergeben jeweils den Komplementärwert 10. Dies gilt für alle Einerstellen in
fortschreitender Multiplikationsreihe.
Die Zahl 1
ist von 0, die Zahl 9
von 10 jeweils einen Zähler entfernt. Wenn die Zahl 9
von 90 9
Zähler entfernt ist, ist die Einerstelle der 9.
Multiplikation 1 und somit in
spiegelsymmetrischer Position der Ausgangszahl 1.
Dieses Prinzip gilt auch für die übrigen Reihen, sowohl horizontal als auch
vertikal.
Die Folge ist ein zweites Palindrom 1-9-1, das vom ursprünglichen Mittelpunkt 1 ausgeht und die
nächste Eckzahl 9 zum Mittelpunkt macht.
3. Die
ausgefüllte Tabelle hat folgende Gestalt:
|
|
Die
Tabelle besteht aus zwei Hälften gleicher Zahlen, die durch eine Diagonale von 9 Quadratzahlen
miteinander verbunden sind. Das entsprechende Zahlenverhältnis der Positionen
ist 36:9:36 = 9*(4:1:4). Die 81 Zahlen sind auf
Punkte gesetzt und durch Linien miteinander verbunden, sodaß die
Multiplikationswerte wie auf einem Koordinatensystem abgelesen werden können.
4. Die
Tabelle kann entweder horizontal von unten nach oben oder vertikal von links
nach rechts reihenweise aufgebaut werden, bis nach der letzten Reihe ein volles
Quadrat entstanden ist. Das Quadrat hat nun von außen gesehen vier gleiche
Seiten und von innen die Zahl 25 als Mittelpunkt, durch den vier Achsen verlaufen. Von innen her dehnen sich nach
außen vier konzentrische
Quadrate aus. Deren verschiedene Zahlenaspekte gilt es nun zu untersuchen.
IV. Die
einstellige 1x1-Tabelle und das SATOR-Quadrat
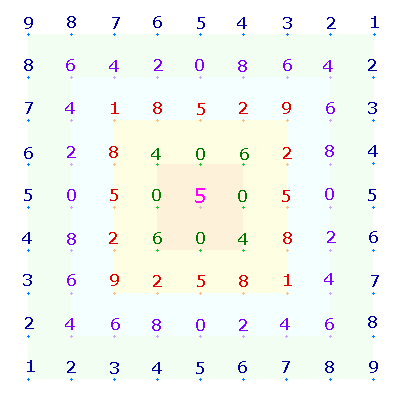
1.
Eine besondere Qualität gewinnt die 1x1-Tabelle, wenn man die
Zehnerziffern wegläßt:
|
|
Das
Tabellenquadrat ist gekennzeichnet durch zwei Gestaltungsprinzipien, Komplementarität und Spiegelbildlichkeit. Ersteres bedeutet,
daß in jeder vertikalen und horizontalen Reihe die Zahl 5 oder die Null den Mittelpunkt für 4
symmetrische Zahlenpaare bilden, deren Summe jeweils 10 beträgt. Das Prinzip
der Spiegelbildlichkeit besagt, daß 2 Zahlen in spiegelsymmetrischer Position
gleich sind. Zu den 9*4 Zahlenpaaren kommen noch 4 Paare aus einer Mittelachse hinzu
36+4 = 40 gleiche Zahlenpaare kreisen also symmetrisch
um den innersten Punkt des Quadrats. Wenn sich jedes Paar zur Summe 10 ergänzt, müßte die
Gesamtsumme 400+5 sein. Da jedoch 4 Paare ohne Zahlenwert, also null statt 10 sind, reduziert sich das Gesamtergebnis 36*10 +5 = 365. Diese Zahl
entspricht den Tagen eines Jahres, die einen Bezug haben zu dem Kreismodell von
3 Hexagonachsen und dem Doppelaspekt von 6 Radial- und 5 Durchmesserelementen.
2. Weist
man dem Mittelpunkt eine gesonderte Bedeutung zu, lassen sich 4 Quadratrahmen (QR) unterscheiden. Der
innerste besteht aus 8 Zahlen, der jeweils größere um jeweils weitere 8 Zahlen. Es ergeben
sich folgende ZS+FS:
|
|
5 |
4 |
|
|||
|
|
MP |
QR1 |
QR2 |
QR3 |
QR4 |
sm |
|
P |
1 |
8 |
16 |
24 |
32 |
81 |
|
ZS |
5 |
20 |
80 |
100 |
160 |
365 |
|
FS |
5 |
18 |
66 |
86 |
142 |
317 |
|
sm |
10 |
38 |
146 |
186 |
302 |
682 |
|
diff. |
– |
2 |
14 |
14 |
18 |
|
|
|
16 |
32 |
48 |
|||
|
682 = 22*31; 186 = 6*31 |
||||||
Die QR1 und QR3 enthalten die
Null-Positionen. Sowohl ihre ZS als auch FS betragen die Hälfte der beiden anderen QR:
|
|
QR1 |
QR3 |
sm |
QR2 |
QR4 |
sm |
|
ZS |
20 |
100 |
120 |
80 |
160 |
240 |
|
FS |
18 |
86 |
104 |
66 |
142 |
208 |
|
|
|
|
224 |
|
|
448 |
|
312:360 = 24*(13:15) |
||||||
Eine Korrespondenz der
ZS+FS zwischen QR2 und QR4 besteht, wenn jedem
die Mittelpunktswerte hinzugefügt werden:
|
|
MP |
QR2 |
sm |
MP |
QR4 |
sm |
GS |
|
ZS |
5 |
80 |
85 |
5 |
160 |
165 |
250 |
|
FS |
5 |
66 |
71 |
5 |
142 |
147 |
218 |
|
|
|
|
156 |
|
|
312 |
468 |
|
156:312 = 12*13*(1:2) |
|||||||
Fügt man beiden
anderen QR 1 und 3 nur einmal die
Mittelpunktswerte hinzu, ergeben die ZS+FS die Hälfte er ersten beiden QR, außerdem noch
getrennt nach ZS und FS:
|
|
MP |
QR1 |
QR3 |
GS |
|
ZS |
5 |
20 |
100 |
125 |
|
FS |
5 |
18 |
86 |
109 |
|
|
|
|
|
234 |
Mittelpunkt und die QR 1 und 2 sind den 5 DM-Elementen des
Kreises, die QR 3 und 4 den 4 Erweiterungselementen des Tetraktyssterns vergleichbar. Wie das
Flächenverhältnis des Hexagonkreises zum äußeren Kreisring 1:2 beträgt, so auch das
Differenzsummenverhältnis 16:32 der beiden Quadratbereiche.
Die Differenzsummen verteilen sich
folgendermaßen auf die Zahlen 6, 8 und 9:
|
|
6 |
8 |
9 |
|
|
Hfk. |
12 |
12 |
4 |
28 |
|
ZS |
72 |
96 |
36 |
204 |
|
FS |
60 |
72 |
24 |
156 |
|
|
132 |
168 |
60 |
360 |
|
Diff. |
12 |
24 |
12 |
48 |
Das FS:ZS-Verhältnis der drei
Zahlen beträgt 12*(13:17)., das Differenzverhältnis 12*(1:2:1).
3. Vom
Palindromcharakter des äußeren Quadratrahmens wurde bereits oben gesprochen. Ein Palindrom des äußeren
Quadratrahmens läuft stets über einen rechten Winkel, umfaßt also 8+1+8 = 17 Zahlen und kann von
jeder Ecke aus angesetzt werden.
Dieselbe
Palindromstruktur gilt auch für die 3 übrigen konzentrisch nach innen gebildeten Quadrate: 6+1+6 = 13, 4+1+4 = 9, 2+1+2 = 5.
4. Für die
Ermittlung der Palindromzahlen der 4 Quadratrahmen sind nur die Punkte, nicht aber
die Linien berücksichtigt worden. Letzteres aber geschieht im SQ, da ja die Buchstaben
S und R den Zahlen 18 und 17 entsprechen. Ein
Palindrom über rechten Winkel besteht aus 9 Punkten + 8 Linien. Einmal ist der Mittelpunkt doppelt zu
zählen.
5. Der
bisherige Vergleich des SQ mit der einstelligen 1x1-Tabelle hat die nicht unbedeutende Erkenntnis
gebracht, daß sein Palindromcharakter auf den quadratischen Umlauf von jeweils
zwei im rechten Winkel stehenden Seiten besteht. Wenn aber der linke untere
oder auch ein anderer Eckpunkt zum Symmetriemittelpunkt zweier im rechten
Winkel auseinanderstrebender Zahlenreihen wird und von den Winkelenden her ein
Palindrom entsteht, so muß dies auch für den eigentlichen Mittelpunkt und
gleichfalls für die Mittellinien der 5 Zeilen gelten. Dies ist der Ausgangspunkt für
das eigentliche SATOR-Quadrat.
V. Die Dreifachzählung des SATOR-Quadrats
1. Die
Untersuchung der Palindromstruktur des SQ hat zwei zwei
Aussagen je Hälfte ergeben:
NET
OPERA SATOR – Es webt die Werke der Schöpfer.
SATOR
OPERA TENET– Der Schöpfer erhält seine Werke.
2. Damit
das Quadrat nun nicht lediglich in zwei Teile zerfällt, binden die 5 Wörter des Quadrats
die zweimal drei Wörter zusammen.
Von
einem solchermaßen komplexen und vollkommenen Wortgebilde erwartet man, daß die
einzelnen Teile und das Ganze durch die Zahlenwerte bestätigt werden. Dies ist
auch hier unter Einbeziehung der Faktorenwerte (FW) der Fall.
Durch dreifache Zählung werden die 4 symmetrischen Wörter
je 3-mal und TENET viermal erfaßt, davon
der Mittelbuchstabe N fünfmal. Das ergibt an Buchstaben 3*4*5 = 60 + 4*5+1 = 21, zusammen 81 Buchstaben. Die Zahl 81 entspricht den 9*9 Zahlen der 1x1-Tabelle, aber auch
der Zahl der Elemente des 5*5 Quadrats: 25 Punkte + 16 Quadrate + 40 Linien. Die Dreifachzählung liefert folgende
Ergebnisse:
|
|
ZS |
*6 |
|
ZS |
*4 |
GS |
FS |
*6 |
|
FS |
*4 |
GS |
|
SATOR/ROTAS |
69 |
414 |
TENET |
61 |
244 |
|
54 |
324 |
TENET |
61 |
244 |
|
|
OPERA/AREPO |
52 |
312 |
1*N |
13 |
13 |
|
40 |
240 |
1*N |
|
13 |
|
|
|
|
726 |
|
|
257 |
983 |
|
564 |
|
|
257 |
821 |
|
983 = 7*139 |
||||||||||||
Die Differenz zwischen
der FS
821 und
der ZS 983 beträgt 3*(2*27) = 162.
|
|
ZS |
FS |
sm |
*6 |
Fkt. |
|
ZS |
FS |
sm |
*4 |
GS |
|
SATOR/ROTAS |
69 |
54 |
123 |
738 |
18*41 |
TENET |
61 |
61 |
122 |
488 |
|
|
OPERA/AREPO |
52 |
40 |
92 |
552 |
24*23 |
1*N |
13 |
13 |
|
26 |
|
|
|
|
|
|
1290 |
|
1804 = 4*11*41 |
514 |
1804 |
|||
Die Gesamtsumme 1804 ist wie die ZS+FS 123 von SATOR durch 41 teilbar. Also sind
die vereinigten Summen 552+514 = 1066 von OPERA und TENET ebenso durch 41 teilbar. Die Summen 738:1066 bilden das Verhältnis 82*(9:13). Das Verhältnis 9:13 läßt sich von der
Zahl 22 = 2*11 = FW 13 her sehen. 9 ist also die
Differenz zwischen dem FW 13 und dem ZW 22. Hinter diesem Verhältnis verbergen sich zwei Achsenkreuze, ein
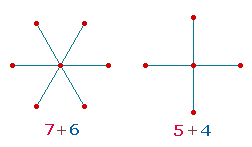
rechtwinkliges aus zwei Achsen und ein hexagonales Achsenkreuz aus drei Achsen:
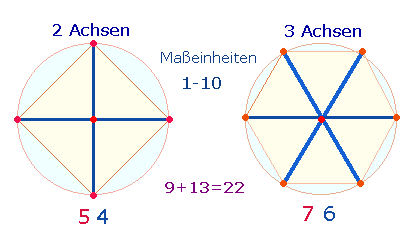
Die
beiden Achsenkreuze sind auf die grundlegenden 10 Maßeinheiten des Dezimalsystems ausgerichtet.
Die Einzelziffern weisen auf die 13 Punkte des Tetraktyssterns hin, in dem die
Zahl 10 nicht nur durch die
Punkte der Tetraktys vertreten ist, sondern durch 10 Maßeinheiten der
Doppelraute, aufgeteilt in 2 Querlinien und 8 Rahmenlinien:
|
|
3. Die
Wörter OPERA und TENET sind also auf SATOR ausgerichtet. Die eine Zahl 123 definiert den
Schöpfergott als dreigestaltig. Im Tetraktysstern ist der trinitarische Gott
durch drei Doppelrauten dargestellt. Je zwei können zu einem Oktaeder aus 41 Elementen zusammengefügt
werden. In einer DR können von jedem Ende her drei geometrische Figuren aus 11, 13 und 17 Elementen erkannt
werden, die zusammen 82 ergeben.
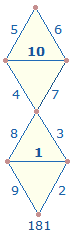
Das FS:ZS-Verhältnis von SATOR ist 3*(18:23). Die Zahlen 18-23 ergeben die Summe 123 und stellen Anfang
und Ende einer DR-Numerierung dar:
|
|
Die FS der 6 Zahlen ist 82, woraus sich das FS:ZS-Verhältnis 41*(2:3) ergibt, vergleichbar mit dem FS:ZS-Verhältnis 21*(2:3) des Namens VESTA. Das interne Differenzverhältnis zur ZS ist jeweils 2:1, sodaß letzteres – als Radialelemente eines Radius – auch
die Erweiterung zu 5 DM-Elementen
beinhaltet.
Das Verhältnis 9:13 ist auf die Elemente von 2 und 3 Achsen zu beziehen:
|
|
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
NET |
158 |
131 |
289 |
81 |
131 |
212 |
501 |
|
SOT |
182 |
155 |
337 |
|
|
|
|
|
|
|
|
626 |
|
|
|
|
|
SATOR |
303 |
249 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZS |
FS |
sm |
sm2 |
FW1 |
FW2 |
sm |
GS |
|
NET*2 |
158 |
131 |
289 |
578 |
|
|
|
|
|
SOT*2 |
182 |
155 |
337 |
674 |
|
|
|
|
|
|
|
|
626 |
|
|
|
|
|
|
SATOR |
303 |
249 |
|
552 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Erstellt: November
2009
Letze Änderung:
August 2010