Das SATOR-Quadrat und die Quadratform
des Einmaleins
B. SATOR-Quadrat und
einstelliges 5x5-Quadrat
Anmerkung: Die Zusammenschau der beiden Quadrate ist inzwischen
(Mai 10) übersichtlicher und schlüssiger in meinem italienischen Beitrag La tavola pitagorica ed il quadrato del sator dargestellt. Dennoch sind
Einzelaspekte von I.u.II. beachtenswert. Die Ergebnisse der Dreifachzählung
(III.) stützen die Gesamtkonzeption des SATOR-Quadrats.
I. Ordnungen des 5x5
Quadrats
II. Beziehungnen zwischen 5x5Q, Doppelraute und SQ
III. Dreifachzählung beider Quadrate
A. Das Prinzip des Außen und Innen
I.
Die Ordnung des 5x5 Quadrats
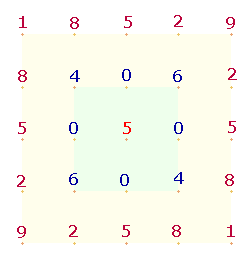
1. Das
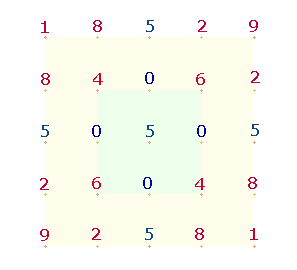
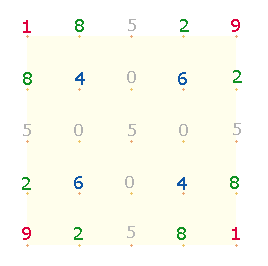
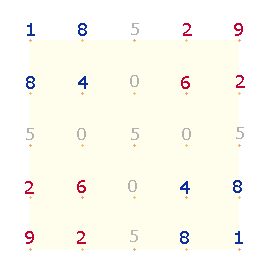
innere 5*5 Punkte Quadrat der einstelligen Einmaleins-Tabelle sei mit 5x5Q abgekürzt:
|
|
|
Das Achsenkreuz läßt 4 Quadrate aus je 4 Zahlen entstehen. Je
zwei diagonale Quadrate sind spiegelsymmetrisch identisch. Der weiteren Betrachtung
sollen die unteren beiden Quadrate (linke Fig.) dienen:
|
2 |
6 |
0 |
4 |
8 |
|
9 |
2 |
5 |
8 |
1 |
Je zwei symmetrisch
zur Mitte stehende Zahlen haben die komplementäre Summe 10, z.B. 9+1, 2+8. Die quadratische Gruppierung zu jeweils 4 Zahlen
lenkt die Aufmerksamkeit eher auf jeweils zwei nebeneinander stehende Zahlen,
z.B. 92, 81. Die vier
zweistelligen Zahlen und ihre Umkehrungen ergeben folgende Faktorenwerte (FW):
|
|
|
|
sm |
|
|
sm |
GS |
|
|
92 |
81 |
173 |
26 |
48 |
74 |
247 |
|
FW |
27 |
12 |
39 |
15 |
11 |
26 |
65 |
|
|
293 |
93 |
212 |
41 |
59 |
100 |
312 |
|
|
29 |
18 |
47 |
62 |
84 |
146 |
193 |
|
FW |
29 |
8 |
37 |
33 |
14 |
47 |
84 |
|
|
58 |
26 |
84 |
95 |
98 |
193 |
277 |
|
GS |
177 |
119 |
296 |
136 |
157 |
293 |
589 |
Die
Gesamt-FS ist 65+84 = 149. (Zur Zahl 149 siehe einige Bedeutungen)
Bemerkenswert
ist das FS:ZS-Verhältnis der
unteren Reihe 65:247 = 13*(5:19). Den 3 Ergebniswerten
13, 5, 19 entsprechen die
Buchstaben NET– er webt des SQ. Es ist nicht
auszuschließen, daß Catull deshalb in seinem c5c7 Quadrat die Primzahl 149 als Faktor der beiden
Achsen gewählt hat.
2. Etwas
größere Aufmerksamkeit verdient das FS:ZS-Verhältnis der Einzelzahlen der beiden
Quadrate, für sich selbst und im Hinblick auf das SQ:
|
|
|
|
|
|
sm |
|
|
|
|
sm |
GS |
|
Z |
9 |
2 |
2 |
6 |
19 |
8 |
1 |
4 |
8 |
21 |
40 |
|
FW |
6 |
2 |
2 |
5 |
15 |
6 |
1 |
4 |
6 |
17 |
32 |
|
|
|
|
|
|
34 |
|
|
|
|
38 |
72 |
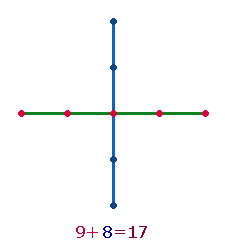
Das FS:ZS-Verhältnis beträgt 8*(4:5). Die Summe der
Einzelziffern 8+9 = 17 läßt sich auf das Achsenkreuz eines 5*5-Punkte Quadrats beziehen.
Die eine Achse besteht aus 4 Linien und 5 Punkten, die zweite aus 8 Ergänzungselementen (ohne Mittelpunkt):
|
|
Als
Parallele sei hier angeführt, daß der Name MARIA dasselbe FS:ZS-Verhältnis 32:40 besitzt.
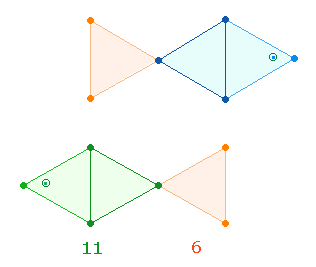
3. Die Ziffern
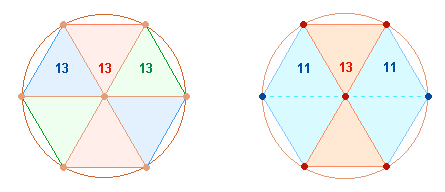
der vierten Zeile haben als zusammengesetzte Zahlen 26 und 48 trinitarische
Bedeutung. Die Doppeldreiecke des Hexagons können auf zweierlei Weise gesehen
werden:
|
|
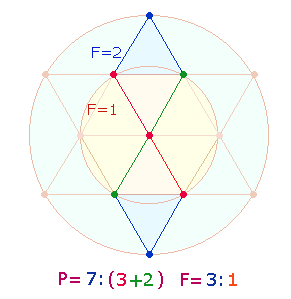
In der
linken Figur besteht jedes Doppeldreieck aus 13 Elementen, in der linken stehen
einander zwei Rautenfiguren aus je 11 Elementen gegenüber, die durch das mittlere
Doppeldreieck verbunden sind. Unter trinitarischem Gesichtspunkt geht die
zweite Person abbildhaft aus der ersten hervor, die dritte Figur stellt die
Beziehung zwischen erster und zweiter Person dar. Die mittlere geometrische
Figur ist jeweils gleich, für sie gilt die Summe 26. Die Figuren der
ersten und zweiten Person sind jeweils 13+11 = 24, zusammen 48. Der Summe 74 entsprechen die
Elemente von zwei Tetraktys.
II. Beziehungnen zwischen 5x5Q, Doppelraute
und SQ
a) 5x5Q und
Doppelraute
b) Die Numerierung 1-18 der DR
c) Die vereinigten Zahlensummen des 5x5Q und des SQ
d) Die vereinigten Faktorensummen des 5x5Q und des SQ
e) Die ZS und FS der 4 Eckquadrate
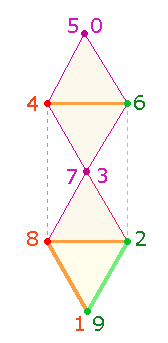
a) 5x5Q und Doppelraute
1.
Wenn man die 7 Punkte der Doppelraute (DR) in achtförmiger
Umfahrung numeriert, zeigt sich in der Anordnung der Zahlen eine auffällige
Parallelität zum 5*5Q:
|
|
Die Zahl
9 kreuzt den ersten
Punkt und kommt neben der 1 zu stehen. In horizontaler Leseweise, von unten nach oben, sind 4
Zahlenpaare zu erkennen, die sich komplementär zu 10 ergänzen. Beginnt man
mit der Zahl 9 und liest die unteren 4 Zahlen kreisförmig gegen den
Uhrzeigersinn, ist die Reihenfolge dieselbe wie in der untersten Zeile des 5x5Q: 92-81.
Mit der
zweiten Zeile des 5x5Q (von unten) stimmen die DR-Zahlen der zweiten und vierten Ebene
zusammen, wieder kreisförmig gegen den Uhrzeigersinn gelesen: 26-48.
2.
Die Zahlen 3 und 7 auf der dritten Ebene
stimmen mit den Grenzen des 5x5Q innerhalb der 1x1-Tabelle überein.
Wenn man
die beiden Querlinien der DR faltet und die Punkte der äußeren beiden Dreiecke vereinigt, läßt
sich zusammen mit einer weiteren DR ein Oktaeder zusammenfügen. Daher kann die 10. Position
der DR neben der 5 mit einer 0 oder 10 besetzt werden. Die Zahlenfolge 5 0 spiegelt die 4
symmetrischen Zahlenpaare des Achsenkreuzes im 5x5Q wider. Die Addition der
zusammengesetzten Zahlen 19+50 = 69 ergibt den ZW von SATOR, die Addition 19+5 die Buchstaben TE – dich und in der Umkehrung ET – und, was inhaltlich der Vereinigung der beiden
DR-Enden entspricht.
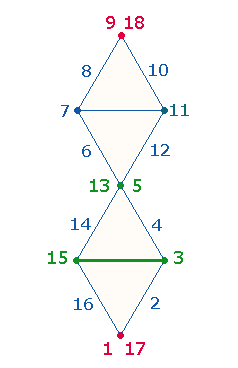
b) Die Numerierung 1-18 der DR
1.
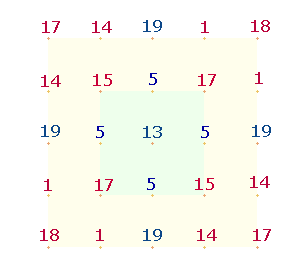
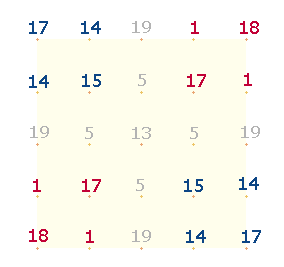
Einen Teil der Frage, welche Beziehung
zwischen dem 5x5Q und dem SQ besteht, beantwortet eine Numerierung des DR-Rahmens, bei der
auch die Linien berücksichtigt werden:
|
|
8 horizontale
Zahlenpaare ergänzen sich zu 18. Vom obersten Zahlenpaar 9+18 befindet sich die Zahl 9 im 5x5Q und die Zahl 18 im SQ in der unteren linken Ecke. Dasselbe
gilt für die untersten Zahlen 1 und 17 der DR. Sie befinden sich im
5x5Q und SQ in der oberen linken Ecke. Auf
diese Weise wird die DR mit den beiden Quadraten verbunden.
2.
Hier ist auf Catulls c5c7-Quadrat zurückzugreifen,
dessen Horizontalachse die ZS+FS 2718 hat. Damit erfaßt Catull die Numerierungssumme des obersten und
untersten Punktes der DR. Er bezieht auch die berühmte Zahl 153 ein, indem er die 18. und 23. Position auf der
Horizontalachse mit den Umkehr-ZS 315 und 351 besetzt:
|
326 |
300 |
331 |
361 |
286 |
|
324 |
217 |
302 |
267 |
280 |
|
325 |
300 |
308 |
315 |
351 |
|
349 |
333 |
358 |
359 |
203 |
|
293 |
266 |
281 |
336 |
348 |
3.
Der Mittelpunkt der numerierten DR wird von den Zahlen 13 und 5 besetzt. Erstere ist
Mittelpunkt des SQ, letztere des 5x5Q.
c) Die vereinigten Zahlensummen des 5x5Q und
des SQ
1.
Die beiden Quadrate haben folgende ZS+FS:
|
|
ZS |
FS |
sm |
|
|
5*5Q |
105 |
89 |
194 |
|
|
SQ |
303 |
249 |
552 |
24*23 |
|
sm |
408 |
338 |
746 |
2*373 |
|
408 = 24*17 |
338=2*13² |
|||
Der Primzahlfaktor 373 des Gesamtergebnisses
gibt die Punkteverteilung des Tetraktyssterns wieder. Die Zahl 24 spielt in
verschiedenen Zahlenverhältnissen eine bemerkenswerte Rolle. Der Tetraktysstern
enthält 24 Linien. Eine wesentliche
Bedeutung haben zwei geometrische Figuren des Hexagon, der DR und des Oktaeders aus
11 und 13 Elementen:
|
|
Der FW von 24 ist 9. Das ergibt das FW:ZW-Verhältnis 3*(3:8), mit dem die FS 338 in einem inneren
Zusammenhang stehen könnte.
Die
beiden Primzahlfaktoren des Gesamtergebnisses eignen sich nicht für addierte ZS+FS-Verhältnisse. ZS und FS sind daher gesondert
zu untersuchen.
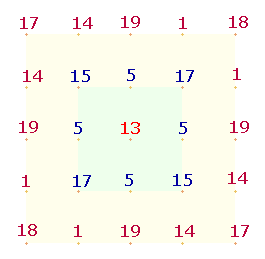
2.
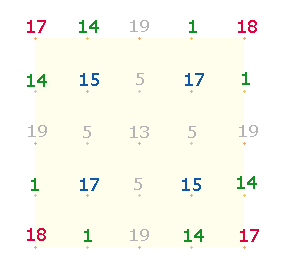
Die 1x1-Tabelle ist geprägt durch konzentrische
Quadratrahmen (QR). Daher ist zu erwarten, daß sie Auskunft geben über die innere
Zusammengehörigkeit des 5x5Q und des SQ:
|
|
|
Die ZS der beiden äußeren QR ist 80+206 = 286, die der inneren 20+84 = 104. Das ZS-Verhältnis der
äußeren zu den inneren QR beträgt 26*(11:4).
Die ZS der beiden geraden
Zeilen 2*(20+52) = 144. Das ZS-Verhältnis der 3 ungeraden zu den 2 geraden Zeilen ist 24*(11:6). Das Verhältnis 11:6 bedeutet eine
Erweiterung der Raute zu einer fischförmigen Figur aus 17 Elementen:
|
|
d) Die vereinigten Faktorensummen des 5x5Q
und des SQ
1.
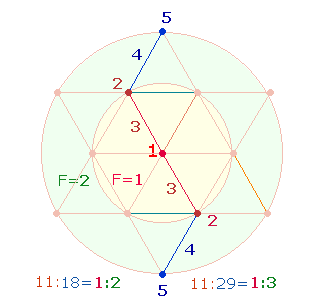
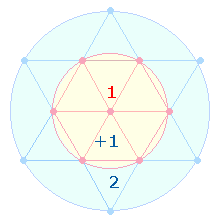
Die FS der beiden Quadrate betragen 89+249 = 338 = 2*13*13. Ein durch 13 teilbares Verhältnis
ist nicht zu erkennen. Die FS der inneren und äußeren QR sind 18+70 = 88 und 66+166 = 232, das Verhältnis 8*(11:29). Im Tetraktysstern
bezeichnen die Numerierungssummen 11:29 das Flächenverhältnis 1:3 der beiden konzentrischen Kreise:
|
|
2.
Zwischen den vier Eckpunkten des äußeren
Quadrats befinden sich 4*3 = 12 mittlere Punkte. Deren FS je Seite sind 13+29 = 42. Das FS-Verhältnis von 12:13 Punkten beträgt somit 168:170 = 2*(84:85). Das entsprechende ZS-Verhältnis beträgt 4*(49:53) = 4*102 = 408.
3.
Die 4 Eckquadrate aus je 4 Punkten sind zu unterteilen in die 4 äußeren Eckpunkten,
die 4*2 ihnen
benachbarten Rand- oder Zuwachspunkte und die 4 inneren Eckpunkte:
|
|
|
Die 8 Randpunkte des 5x5Q und des SQ haben die FS 32:40 = 8*(4:5) = 72. Die FS der äußeren Eckpunkte
sind 14+50 = 64. Das FS-Verhältnis aller
Randpunkte zu allen Eckpunkten ist somit 8*(9:8) = 8*17 = 136. Die Zahl 136 ist die Summe der
Zahlen von 1-16 und gibt die Verteilung der 10 Punkte der Tetraktys wieder.
Die FS der inneren Eckpunkte
sind 18+50 = 68. Das FS-Verhältnis der
äußeren zu den inneren Eckpunkten ist somit 4*(16:17) = 132. Das FS-Verhältnis der 4
inneren Eckpunkte zu den 4 äußeren Eckpunkten und den 8 Randpunkten, d.h. von 4*(1:3) Punkten, beträgt 68*(1:2).
e) Die ZS
und FS der 4 Eckquadrate
1.
Jeweils zwei diagonale Eckquadrate des 5x5Q und des SQ sind gleich:
|
|
|
Die Werte beider
Quadrate stimmen in der Addition der ZS+FS zusammen. Die Werte des unteren linken und
unteren rechten Quadrats sind:
|
|
links |
sm |
rechts |
sm |
GS |
||
|
|
ZS |
FS |
|
ZS |
FS |
|
|
|
5x5Q |
19 |
27 |
46 |
21 |
17 |
38 |
84 |
|
SQ |
37 |
15 |
52 |
60 |
43 |
103 |
155 |
|
|
56 |
42 |
98 |
81 |
60 |
141 |
239 |
|
14*(3:4) |
3*(20:27) |
|
|||||
Die
Primzahl 239, aufgeteilt in (2+3):9, stellt die Durchmesser(DM-) Elemente der beiden konzentrischen
Kreise des Tetraktyssterns dar und gibt deren Flächenverhältnis 1:3 wieder.
2.
Alle Nicht-Primzahlen sind gekennzeichnet
durch eine Differenz (diff.) zwischen FW (aus Addition der Primzahlfaktoren) und Nennwert, hier der
Einfachheit halber Zahlenwert (ZW) genannt. Die Ordnung unter Zahlen wird mitbestimmt durch Verhältnisse
von Differenzsummen. Diese sind auch in den beiden untersuchten Quadraten
wirksam. In der folgenden Tabelle werden nur die Nicht-Primzahlen aufgeführt:
|
|
5x5Q |
sm |
SQ |
sm |
GS |
|||
|
li. Qu. |
9 |
6 |
|
18 |
|
|
|
|
|
diff. |
3 |
1 |
4 |
10 |
|
|
10 |
14 |
|
re. Qu. |
8 |
8 |
|
14 |
14 |
15 |
|
|
|
diff. |
2 |
2 |
4 |
5 |
5 |
7 |
17 |
21 |
|
|
|
|
8 |
|
|
|
27 |
35 |
Das
Differenzsummen-Verhältnis vom linken zum rechten unteren Quadrat ist 14:21 = 7*(2:3). Die Zahl 7 weist auf die Zahl
der DR-Punkte hin, die Zahlen 2 und 3 auf die 5 Punkte des hexagonalen Doppeldreiecks:
|
|
Die Differenzsummen 8 und 27 im 5x5Q und im SQ sind die Kubikzahlen
von 2 und 3, ihre FW 6+9 = 15 sind zu verstehen als
6 Linien und 9 Punkte der drei Hexagonachsen und in
zusammengesetzter Form 69 als ZW von SATOR. Das (externe) Verhältnis dieser Faktorensumme zur Differenzsumme
ist 15:35 = 5*(3:7), das interne
Differenzsummenverhältnis 3:4, das wiederum auf die 7 Punkte der DR verweist.
Die Differenzsumme des
5x5Q ist in jedem Quadrat 4, im SQ einmal 10 und einmal 17. Die Zahlen 10 und 17 lassen sich auf eine
numerierte DR beziehen, von deren 7 Punkten 2+1 Punkte doppelt
besetzt werden. Die überzählige
Numerierung ist (8+9)+10.
1.
Das horizontal-vertikale Achsenkreuze beider
Quadrate besteht – im Unterschied zu den eben behandelten 4 Quadraten – nur aus
Primzahlen: Die ZS ist 25+109 = 134. Die Einzelziffern der Summe sind zu verstehen als (1+3)*4 im Hinblick auf die 4 Quadrate. Die Zahl 1 bezieht sich auf
einen Eckpunkt des inneren Quadrats, die Zahl 3 auf die Winkelpunkte des äußeren
Quadratrahmens.
2.
Der FW der Zahl 134 ist 69 und stellt so einen inneren Zusammenhang
zwischen Quadrat und dem Schöpfergott SATOR her.
III.
Dreifachzählung beider Quadrate
1.
Die Dreifachzählung des SQ wurde im vorhergehenden
Kapitel durchgeführt. In zwei Zählungen werden unterschiedliche Formen
der Symmetriemitte verdoppelt. Einmal ist die Symmetriemitte der Mittelpunkt,
einmal die Mittelzeile. Die Punktezahl (P) bzw. Buchstabenzahl (Bu) ist jeweils 13+15 = 28. Die beiden Aussagen
des SQ sind NET OPERA SATOR (NOS) und SATOR OPERA TENET (SOT):Die ZS+FS der ersten beiden
Zählungen ergeben:
|
|
5x5Q |
|
SQ |
|
|
||
|
P/Bu |
13 |
15 |
sm |
NOS |
SOT |
sm |
GS |
|
ZS |
55 |
60 |
115 |
158 |
182 |
340 |
455 |
|
FS |
47 |
52 |
99 |
131 |
155 |
286 |
385 |
|
|
|
|
214 |
|
|
626 |
840 |
|
385:455 = 35*(11:13) |
|||||||
Die
Differenzsumme muß, wie oben ausgeführt, bei zwei Zählungen 2*35 sein. Aber auch die ZS 455 ist durch 35 teilbar. Die
Verhältniszahlen 11 und 13 verweisen auf Raute
und Doppeldreieck, die Hauptbestandteile der Doppelraute und des Oktaeders.
Das FS:ZS-Verhältnis 11:13 entspricht dem des PATER NOSTER: 121:143 = 11*(11:13).
Erwähnenswert
ist auch das FS-Verhältnis 99:286 = 11*(9:26).
2.
Die dritte Zählung wurde bereits oben genannt.
Sie ist den verdoppelten Werten der ersten beiden Zählungen hinzuzufügen:
|
|
5x5Q |
SQ |
|
||||
|
Zählg. |
1/2 |
3 |
sm |
1/2 |
3 |
sm |
GS |
|
ZS |
230 |
105 |
335 |
680 |
303 |
983 |
1318 |
|
FS |
198 |
89 |
287 |
572 |
249 |
821 |
1008 |
|
|
|
|
622 |
|
|
1804 |
2426 |
Die Gesamtsumme 2426 = 2*1213 ist auf den
Tetraktysstern und seinen beiden Kreisflächen zu beziehen: Das Hexagon besteht
aus 12 Linien und 7 Punkten + 6 Dreiecken. Die
Erweiterungselemente sind identisch, wenn dem äußeren Kreis ein eigener Mittelpunkt
zugestanden wird. Die Zahl 2426 gibt somit das Flächenverhältnis 1:3 der beiden konzentrischen Kreise wieder:
|
|
Das Flächenverhältnis des
inneren Kreises zum äußeren Kreisring ist 1:2.
Die Aufteilung in 2*1213 weist weiterhin
sinnvoll auf die 12 geraden und 13 ungeraden Punkte beider Quadrate hin.
3.
Die Dreifachzählung erfaßt 2*(13+15)+25 = 56+25
= 81
Punkte. Der Zahl 56 entsprechen 16 Einzelquadrate + 40 Verbindungslinien des 5*5 Punkte-Quadrats.
-------------------
4.
Von Bedeutung erscheint die ZS 158 + 182 = 340 = 20*17 von NET OPERA SATOR + SATOR OPERA TENET. Denn ROTA als beherrschendes
Wort der Kreisbewegung hat den ZW 51 = 3*17. Neben ROTA läßt sich SORT (68) als eine durch 17 teilbare Wortgruppe aus 4 Buchstaben
herauslösen. Die beiden Wortgruppen sind jeweils zu verdoppeln wie auch die
weitere aus 5 Buchstaben bestehende PEAEN, während ET nur einmal zu zählen ist.
|
R |
O |
T |
A |
S |
|
O |
P |
E |
R |
A |
|
T |
E |
N |
E |
T |
|
ROTA |
51 |
102 |
2x |
PEAEN |
39 |
78 |
2x |
180 |
|
SORT |
68 |
136 |
2x |
ET |
24 |
24 |
1x |
160 |
|
|
119 |
238 |
|
|
63 |
102 |
|
340 |
|
238:102 = 34*(7:3); 180:160 = 20*(9:8) |
||||||||
Betrachtet
man nur die Zählung der ersten drei Zeilen (SOT), ergibt sich das Verhältnis 119:63 = 7*(17:9) der zwei durch 17 teilbaren Wortgruppen
zu den übrigen 7 Buchstaben (mit Durchschnittswert 9). Unterteilt in 2. und 3. Zeile ist das
ZW-Verhältnis von PEA und ENET 21:41 = 21*(1:2).
Die
Buchstabengruppe PEAEN läßt sich zu dem lateinischen Wort PAENE – fast umformen. Das ZS-Verhältnis zu den übrigen 10 Buchstaben beträgt 39:143 = 13*(3:11). Die ZS 143 entspricht der des PATER NOSTER. Aus den 10
Buchstaben läßt sich der Satz bilden SATOR ROTET – Der Schöpfer möge drehen. Eine Sinndeutung des
PAENE in diesem
Zusammenhang läßt sich nicht erkennen.
Die
Buchstabengruppe SORT stellt den Wortstamm von SORS – Los, Schicksal dar. Die nicht existierende Form SORTATOR würde danach bedeuten,
daß Gott das Schicksal aller Geschöpfe bestimmt.
Erstellt: November 2009, ergänzt August 2010, August 2015 (11pt)