Umkehrungen
dreistelliger Zahlen
VI. Komplementäre Ordnung von 14 Primzahlumkehrungen
a) Drei Gruppen
d) Vereinbarkeit von 709 und 739
a) Drei Gruppen
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
107 |
113 |
149 |
157 |
167 |
179 |
199 |
311 |
337 |
347 |
359 |
389 |
701 |
709 |
|
991 |
983 |
971 |
967 |
953 |
941 |
937 |
907 |
769 |
761 |
751 |
743 |
739 |
733 |
|
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
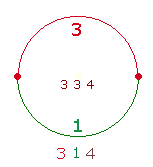
1. Im vorhergehenden Kapitel wurde erkennbar, daß von den 14 Umkehrzahlen sich 4 darin unterscheiden, daß ihe Umkehrungen in
ihrer eigenen Tausenderhälfte liegen, 113 –311, 709 – 907, 739 – 937, 769 – 967. Dies führt zur Annahme, daß sich die 14 Zahlen
aus 10+4 zuammensetzen: aus der Summe der Zahlen 1-4 und aus 4 selbst. Da die Gesamtsumme 16370 durch 10 teilbar ist, liegt es nahe, die Zahlen so in Paaren zu ordnen, daß
ihre Summe jeweils durch 10 teilbar ist.
Voraussetzung für
komplementäre Paare sind Additionen der Einerstellen 1+9 und 3+7:
2.
Die
komplementäre Ordnung ergibt drei Gruppen:
·
5 Zahlenpaare erfüllen die komplementäre
Bedingung auf der ersten und dritten Stelle, daher bedürfen sie zur Teilbarkeit
durch 10 nur ihre eigene Umkehrung:
|
|
|
|
sm |
|
|
sm |
GS |
|
149 |
179 |
199 |
527 |
337 |
347 |
684 |
1211 |
|
941 |
971 |
991 |
2903 |
733 |
743 |
1476 |
4379 |
|
1090 |
1150 |
1190 |
3430 |
1070 |
1090 |
2160 |
5590 |
|
1211 = 7*173 >FW 180; 4379 = 29*151 >180 |
|||||||
|
5590 = 10*13*43 >63 |
|||||||
Diese 10 Zahlen scheiden im weiteren Verlauf der
Untersuchung für die konzentrische Anordnung der übrigen 18 Zahlen aus.
·
Die 9 anderen Zahlenpaare sind in der folgenden
Tabelle konzentrisch angeordnet, d.h. unter der niedrigsten Zahl steht die
höchste. Die ersten drei Paare ergänzen sich zu
einer 10-er Summe, die Ergänzung von vier Paaren ergibt sich durch lineare Verschiebung
der unteren Reihe um eine Stelle, die restlichen 4 Zahlen ergänzen sich durch 3*7 und 1*9:
|
18 |
17 |
16 |
16 |
14 |
13 |
12 |
11 |
10 |
|
107 |
113 |
157 |
167 |
311 |
359 |
389 |
701 |
709 |
|
983 |
967 |
953 |
937 |
907 |
769 |
761 |
751 |
739 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
983 |
967 |
953 |
769 |
761 |
751 |
739 |
5923 |
|
107 |
113 |
157 |
311 |
359 |
389 |
701 |
2137 |
|
1090 |
1080 |
1110 |
1080 |
1120 |
1140 |
1440 |
8060 |
|
8060 = 20*13*31
> 53 |
|||||||
Die sieben Komplementärpaare beginnen mit der Zahl 107 und enden mit ihrer Umkehrung 701. In der von unten ansteigenden Primzahlfolge fällt erstmals 167 aus, da keine 3 als Einerstelle des oberen Zahlenbereichs mehr zur Verfügung steht. Dies gilt umgekehrt auch für 937 und 907 im unteren Zahlenbereich. Schließlich bleibt 709 übrig.
·
Die 4 Zahlen
im Zusammenhang sind:
|
167 |
937 |
907 |
709 |
2720 |
|
1104 |
1616 |
|
||
|
2720 = 160*17 > 32 |
||||
|
1104:1616 =
16*(69:101) |
||||
1.
Die ZW/FW-Verrechnung der drei Summen ergibt:
|
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
5590 |
8060 |
2720 |
16370 |
1644 |
|
|
|
FW |
63 |
53 |
32 |
148 |
41 |
|
|
|
sm |
|
|
|
16518 |
1685 |
|
|
|
FW |
16518 = 2*3*2753 |
2758 |
342 |
3100 |
45 |
||
|
148 = 4*37;
1685 = 5*337; 342 = 18*19 |
|||||||
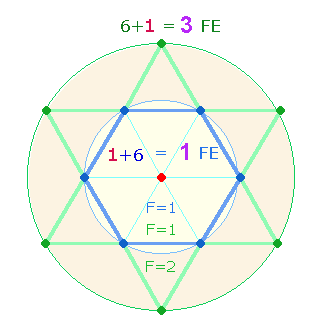
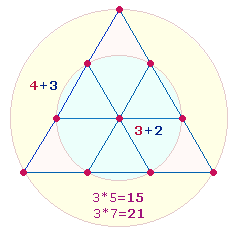
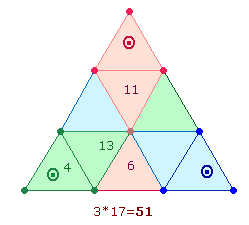
In den Ergebnissen
erkennt man die Ausrichtung auf Hexagramm und Doppelkreis: 337, selbst eine der 14 Umkehrzahlen, gibt in den Einzelziffern die
Punkteaufteilung der 13 Punkte wieder. Das Produkt 18*19 des Faktorenwertes (FW) 342 bezeichnet die
18 Linien und 10 Punkte
+ 9 Dreiecke der Tetraktys.
2.
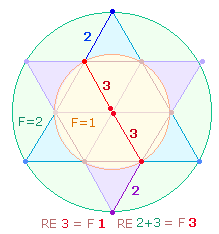
Die
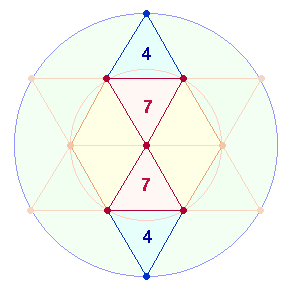
Faktoren der FS 3100 sind 31+7+7 = 45 = 5*9. Wenn um die 6 äußeren
Punkte des Hexagramms ein Kreis geschlagen wird, kommt der 7. Punkt
hinzu. Das Kreisflächenverhältnis dieses
äußeren Kreises zum inneren Kreis beträgt 3:1:
|
|
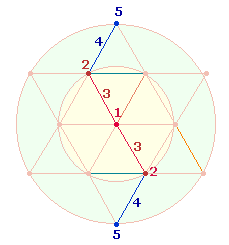
3.
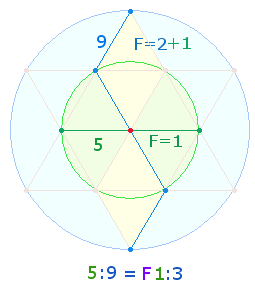
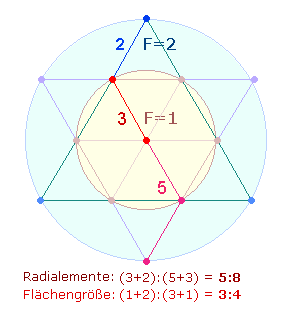
Der FW 45 ist ebenfalls auf die Flächen der beiden
Kreise hin zu interpretieren. 45 ist die Summe
der Zahlen von 1-9. Die Zickzacklinie der (DR) besteht aus 9
Durchmesserelementen, 5 gehören der inneren Kreisachse an, 4 der hexagonlen Erweiterung: 5:4 und 5:9 Durchmesserelemente geben die
Flächenverhältnisse 1:2 und 1:3 wieder:
|
|
1.
Würde
man statt 739 die benachbarte Zahl 709 mit 701 verbinden, liefen die 7 Zahlenpaare vom weitesten Abstand bis zum engsten zu. Es würden dann
die Umkehrzahlen 937 und 739 übrig
bleiben statt den Umkehrzahlen 907
und 709:
|
107 |
113 |
157 |
311 |
359 |
389 |
701 |
2137 |
|
983 |
967 |
953 |
769 |
761 |
751 |
709 |
5893 |
|
1090 |
1080 |
1110 |
1080 |
1120 |
1140 |
1410 |
8030 |
|
8030 = 10*11*73 >
91 |
|||||||
|
167 |
937 |
907 |
739 |
2750 |
|
2750 = 10*11*25 > 28 |
||||
2.
Betrachten
wir nun die FW der drei Gruppen, erkennen wir, daß sie
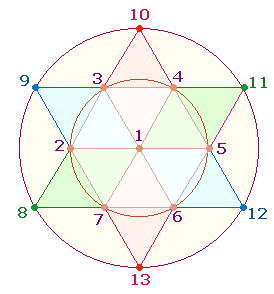
durch 7 teilbar sind: 63+91+28 = 7*(9+13+4) = 7*26 = 182 = 13*14. Die FW sind auf die 7 Punkte
des Hexagons und die 13 Punkte des Hexagramms beziehbar:
|
|
Die Summen der Zahlen von 1-7 und 1-13 sind 28 und 91, die Differenz zwischen beiden ist 63. In
Flächeneinheiten des Doppelkreises ausgedrückt bedeuten die drei FW 63, 91, 28
demnach 2+3+1 = 6 Einheiten. Das Produkt 13*14 ist zu verstehen als 13+(7+7), was 3+(1+3) = 7 Kreisflächeneinheiten entspricht. Die zweite 7 besteht aus 6 äußeren Punkten und einem zusätzlichen Mittelpunkt und
gibt dieselben 3 Flächeneinheiten wieder wie alle 13 Punkte, wie in der oberen Grafik bereits gezeigt wurde.
d) Vereinbarkeit von
709 und 739
1.
Die
zweite Komplementärpaarung erscheint schlüssiger als die erste. Gründe für zwei Lösungen
sind etwa folgende:
·
739 und 709 haben beide ihre Umkehrungen in ihrer eigenen
Tausenderhälfte.
·
Die 8. Zahl ist 701, die nun die Wahl
hat, sich die nächste Zahl 709 zur Partnerin zu wählen oder diese zu überspringen,
um die bisherige konzentrische Ordnung einzuhalten. Wegen der gemeinsamen Null
und der konzentrischen Mitte ist die Paarung 701 – 709 besonders sinnvoll.
·
Wenn die Zahl 739 gewählt wird,
sind beide Umkehrzahlen 907 – 709 zu den vier verbleibenden verbannt, wird 709 gewählt,
geschieht dasselbe mit 937 – 739.
·
739 und 709 bilden die Mitte der nunmehr 18 Zahlen. Von der
untersten Zahl 107 und der obersten Zahl 983 her gesehen nehmen sie beide die 9. Stelle ein.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
107 |
113 |
157 |
167 |
311 |
359 |
389 |
701 |
709 |
739 |
751 |
761 |
769 |
907 |
937 |
953 |
967 |
983 |
Die Tabelle zeigt, daß
zweimal drei zusammenhängende Zahlen (braun, grün unterlegt) 6
konzentrische Paarungen bilden. Von den übrigen 6 Zahlen
liegen 3
(weiß unterlegt) als nicht komplementierbar fest. Dadurch verschiebt sich die
parallele konzentrische Zuordnung der grün unterlegten
um einen Zähler.
Die Summen der vier
verschieden unterlegten Positionen betragen von links nach rechts 12+13+39+26 = 90. Durch Gruppierung 12+39 = 51 und 13+26 = 39 erhält man das Verhältnis 3*(17:13). Zwei durch 13 teilbare Verhältnisse sind 13*(1:3)
und 13*(1:2).
2.
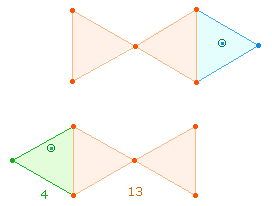
Trinitarisch
läßt sich die Summe der mittleren drei Primzahlen interpretieren: 701+709+739 = 2149 = 7*307 >FW 314. Der FW ist
verstehbar als 3+14: 3 Flächen
und 14 Elemente der "Fischfigur" und als trinitarische Gleichung 3+1 = 4, bezogen auf die Punkte der Doppelraute, die
aus zwei Rauten und je 4 Punkten
besteht. Die 7 Ziffern der drei Zahlen haben die Quersumme 43 und geben in den Einzelziffern die 4 Dreiecke
der DR und 3 Dreiecke
der "Fischfigur" wieder, ebenso 4+3 Punkte
der DR.
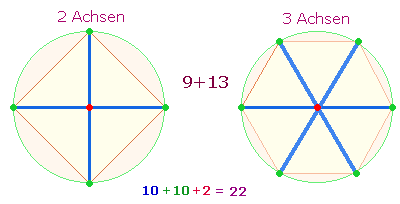
3.
Auch die
Tabellenpositionen der 3+1 Zahlen der 3.
Gruppe haben ihre Bedeutung: Aus 5+4 Elementen
besteht ein Achsenkreuz aus zwei Achsen, das durch 4 weitere Elemente zu den drei Achsen des
Hexagons erweitert wird. Die 9. Position
vertritt das einfache Achsenkreuz:
|
|
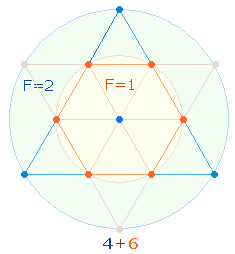
Durch die beiden
Achsenkreuze werden 4+6
= 10 Maßeinheiten dargestellt.
Sie bilden ein wesentliches Modell des Dezimalsystems.
Wenn man als 9. Position die Zahl 739 nimmt, ergibt sich für 4:2 Zahlen (weiß und gelb unterlegt) das
Verhältnis 2720:1440 = 160*(17:9).
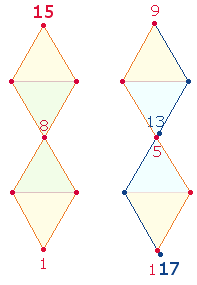
1.
Zwischen
beiden Zahlenpaaren 709
– 907 und 739 – 937 besteht offensichtlich eine besondere
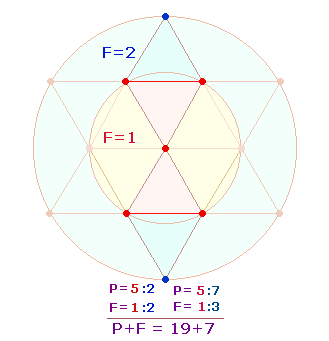
Beziehung. Sie wird sichtbar durch Kreuzaddition 709+937 = 1646, 907+739 = 1646 = 2*823. Die Primzahl 823 ist zu lesen
als Doppelaspekt von (5+3)+(2+3) Radialelementen der zwei konzentrischen
Kreise des Hexagramms; Radialelement treten im Kreis nach zwei Seiten auf, was
den Faktor 2 erklärt:
|
|
Die Kreisflächenentsprechung der aufgeteilten
Radialelemente beträgt 3:1 und
2:1. Die Einzelziffern der Zahl 1646 geben die 7 Punkte
des Hexagons und 10 Punkte der Tetraktys sowie die analogen Kreisflächeneinheiten
1+(3+1) wieder.
1. Die Einzelziffern von 5 Primzahlpaaren ergänzen sich zu jeweils 10, so daß die Summe jeweils 1110 beträgt:
|
113 |
157 |
199 |
337 |
359 |
1165 |
5*233 |
238 |
26 |
|
997 |
953 |
911 |
773 |
751 |
4385 |
5*877 |
882 |
22 |
|
|
|
|
|
|
5550 |
|
1120 |
48 |
|
5550 = FW 52 1120 = FW 22; 52:22 = 2*(11:26) = 2*37 |
||||||||
|
26:22
= 2*(13:11) |
||||||||
Die Faktoren 233 und 877 sind
ebenfalls komplementäre Primzahlen mit der Summe 1110.
Die Verrechnung der ZS 5550 und FS 1120 führt zu je 37 Elementen von zwei Tetraktys, das Verhältnis 2*(13:11) weist auf zwei geometrische Figuren hin, aus denen die Oberfläche des Oktaeders zusammengesetzt ist.
Die Zahlen 157 und 953 sind ein zweites Mal als ihre Umkehrungen 751 und 359 vertreten. Sie scheiden bei der folgenden
Umkehrbetrachtung aus.
2. Von den 5 Primzahlpaaren lassen sich 3 Umkehrungen mit Komplementärzahlen bilden:
|
311 |
991 |
733 |
2035 |
311 |
911 |
733 |
2035 |
4070 |
|
799 |
119 |
377 |
1295 |
64 |
24 |
42 |
130 |
1425 |
|
|
|
|
3330 |
|
|
|
2165 |
5495 |
|
5495
= 5*7*157 >169 = 13²>26 ; 2165 = 5*433 > 438 = 6*73>78 |
||||||||
|
26:78 = 26*(1:3) |
||||||||
Hervorzuheben ist das ZS-Verhältnis 2035:1295 = 5*37*(11:7). Das Verhältnis 11:7 bezieht sich auf die 11
Elemente der Raute,
von denen 7 zum hexagonalen Bereich gehören, es gibt das Kreisflächenverhältnis 3:1 wieder:
1. Die Zahlen 157, 359, 751,
953 gerieten durch einen selektiven Prozeß in den Blickpunkt. Zuerst befinden
sie sich unter den 14 Paaren primer Umkehrzahlen. Dann wurden 5 Paare
herausgefunden, deren Einzelziffern sich in den Einer-, Zehner- und
Hunderterstellen zu je 10 ergänzen. Die Einmaligkeit der 4 genannten Zahlen
ist, daß je zwei Komplementärzahlen auch in ihrer Umkehrung Primzahlen sind.
Dies läßt eine besondere Zusammengehörigkeit der zwei Zahlenpaare vermuten.
2. Die Bedeutungen der beiden
Ausgangszahlen 157 und 359 sowie ihrer Umkehrungen
scheinen sich hauptsächlich aus ihren Einzelziffern zu erschließen. Letztere ist eher leicht, erstere jedoch
schwer zu deuten. Beginnen wir mit letzterer.
Die Zahlen 5 und 9 gehen jeweils aus der vorherigen mit ihrer
niedrigeren Konstitutivzahl hervor, als 3+2 = 5, 5+4 = 9; 3 selbst
entsteht aus 2+1. In zweistelliger Zusammensetzung ergibt sich
(21+32)+54 = 53+54 =
107, auf zuteilen in 10 Tetraktyspunkte und 7 Hexagonpunkte.
Die Zahlen 3+5 und 5+9 sind auf die Radial- und Durchmesserelemente
einer Zickzacklinie der DR zu beziehen. Sie stellen innerhalb der beiden
konzentrischen Tetraktyskreise 1:3 Flächeneinheiten dar:
|
|
|
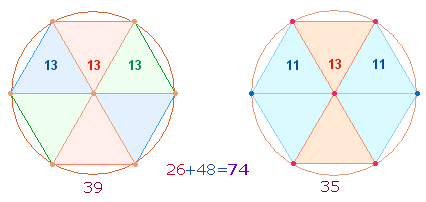
Die zusammengesetzten Zahlen 35 und 39 haben trinitarische Bedeutung, weil sie die
Elemente von jeweils drei geometrischen Figuren im Hexagon darstellen:
|
|
Die Summe 74 weist auf 2*37 Elemente von zwei Tetraktys voraus.
In zweistelliger Zusammensetzung ergibt 35+59+39 133 = 7*19. Die
Einzelziffern weisen auf die Punkteverteilung der DR hin:
Mittelpunkt + zweimal 3 symmetrische Punkte. 5:7 und 5:2 Punkte,
zusammen 19 Punkte repräsentieren 7 Kreisflächeneinheiten:
|
|
3. Die Zahl 157 ist von den
Einzelziffern der doppelten Summe 314 her zu sehen, die einen Bezug zum Kreis
in der Kreiszahl PI (p) 3,14 hat. Die Ziffern genügen der Gleichung 3+1 = 4,
die zweimal die Punkte der
DR wiedergibt, wobei der
Mittelpunkt zweimal zu zählen ist. In einfacher Zählung erkennt man den
Kreisbezug im Kreisbogen, der durch zwei Punkte halbiert wird:
|
|
Zählt man 2*3 Elemente
für je eine Hälfte und 4 Elemente für zwei Hälften zusammen, erhält man die
systemrelevante Summe 10.
Die Verdoppelung des Mittelpunktes der DR spielt
auch eine Rolle für die Einzelziffern 1 5 7. Den
3 Achsen des Hexagons zu je 5 Elementen
entsprechen 3 Tetraktysseiten zu je 7 Elementen:
|
|
Die Zahl 1 bezeichnet den Mittelpunkt. 1 und 5 sind demnach doppelt zu lesen: (1+5)+5 = 6+5
= 11. Zu zählen sind 6 Radial- und 5 Durchmesserelemente. Die Zahl 6 gilt jedoch auch für eine Tetraktysseite. Denn alle drei Seiten
zusammen bestehen aus 9 Punkten und 9 Linien,
also aus 18 Elementen und je Seite aus 6 Elementen.
Damit kommt ebenfalls eine Doppelzählung von 7+6 = 13 Elementen je Seite zustande. Für drei Achsen
und drei Seiten ergibt sich die Summe 3*(11+13) = 72.
Da nun die Gestalt der
DR zwei Tetraktys voraussetzt, ist die Verdoppelung
der Zahl 157 zu 314 sinnvoll.
Freilich kann man die
drei Einzelziffern auch auf die Punkte der DR selbst
beziehen: 5:7 Punkte geben das Kreisflächenverhältnis 1:3 wieder und 1+7 Punkte
ergeben wiederum 8 DR-Punkte bei
zwei Mittelpunkten.
Auch die Zusammensetzungen 15 und 17 sind in
der DR relevant:
|
|
Rechts werden die 15 Rahmenelemente der DR in
schleifenförmiger Umfahrung gezählt, bis der Ausgangspunkt wieder erreicht ist.
Dadurch werden 2 Positionen hinzugewonnen.
4. Die systemrelevante Zahl 10 zeigt sich in den
Einzelziffern der Faktoren der Addition 157+359 = 516 = 12*43 = FW 50.
Aus je 25 Elementen besteht das Hexagon und seine Erweiterung, wenn für letztere
der Mittelpunkt ein zweites Mal zählt.
In zweistelliger Zusammensetzung ergeben sich
für beide Zahlen folgende ZS und FS:
|
15 |
17 |
57 |
89 |
35 |
39 |
59 |
133 |
222 |
|
8 |
17 |
22 |
47 |
12 |
16 |
59 |
87 |
134 |
|
23 |
34 |
79 |
136 |
47 |
55 |
118 |
220 |
356 |
|
89+(47+220) = 89+267; 89:267 = 89*(1:3) |
||||||||
Die ZS+FS der 12 Werte
ist 4-mal die ZS 89. Aus 8+9
Elementen besteht eine Oktaederhälfte, aus 8 Linien und 9 Punktepositionen die schleifenförmige Umfahrung der DR-Elemente, aus 8 Linien und 6 Punkten + 3 Flächen die "Fischfigur", die im DR-Kreuz 4-mal vorhanden ist:
|
|
Den 13+4 Elementen der Fischfigur entspricht auch die
Gesamt-FS 134, die wiederum als Gleichng 1+3 = 4 die 8 Punkte der DR darstellt.
Einmal 89 ergibt sich aus der Addition der ZS+FS 34+55.
1. Um zu erkennen, wie die
Primzahlen 157 und 359 zusammengehören, ist es nützlich, die jeweils 6
Umkehrungen mit ihren FW zu ermitteln.
Die ZS einer dreistelligen
Zahl mit drei verschiedenen Einzelziffern ergibt sich aus der doppelten
Quersumme mal 111. Die doppelte Quersumme der beiden Zahlen
ist also 2*13 = 26 und 2*17 = 34,
die Gesamt-ZS 111*(26+34) = 6660.
Die beiden doppelten Quersummen verweisen auf den Oktaeder, der aus 26 Elementen als ganzer und aus 2*17 je Hälfte besteht. Da zur Oktaederbildung
die äußeren Punkte einer DR verbunden
werden, entsteht ein zweites Doppeldreieck aus 13
Elementen. Dazu kommen zwei Fischfiguren aus je 17 Elementen,
wie in obiger Grafik bereits veranschaulicht.
Die Umkehrungen mit ihren FW sind:
|
Zahl |
157 |
175 |
517 |
571 |
715 |
751 |
2886 |
359 |
395 |
539 |
593 |
935 |
953 |
3774 |
6660 |
|
FW |
157 |
17 |
58 |
571 |
29 |
751 |
1583 |
359 |
84 |
25 |
593 |
33 |
953 |
2047 |
3630 |
|
|
232 |
1819 |
1579 |
|
|
||||||||||
|
|
314 |
192 |
575 |
1142 |
744 |
1502 |
4469 |
718 |
479 |
564 |
1186 |
968 |
1906 |
5821 |
10290 |
Entsprechend den
beiden Quersummen 13+17
= 30 ist die FS 3630 durch 30 teilbar und ermöglicht ein Zahlenverhältnis
zur ZS: 3630:6660 = 30*(121:202) = 30*343 = 30*7³. 121
verweist durch die Faktoren 11*11 auf die DR, 7³ auf die
3*7 Elemente der Tetraktysseiten.
2. Vier Zahlen 517, 715, 539, 935 sind durch 11 teilbar: (47+65+49+85)*11 = 246*11. Für 246 sind drei
Bedeutungen anzumerken:
·
In die Fischfigur
aus 17
Elementen, je dreimal in 2 Tetraktys vertreten, sind die Raute und das
sanduhrförmige Doppeldreieck aus 11 und 13 Elementen integriert. Auf diese Weise kommen 6*41 = 246 Elemente
zustande:
|
|
·
Aufgeteilt in 2*(4+6) ist an zweimal 10 Tetraktyspunkte zu denken:
|
|
Die
Punkteaufteilung gibt das Kreisflächenverhältnis 3:1 wieder.
·
In der Aufteilung
24+6
tritt sie als Addition der 3 komplementären Zahlenpaare 9+8+7 und 1+2+3 auf.
Die FW der 4 mit dem
Faktor 11 verbundenen Ergebnisse 47+65+49+85 sind 47+14+18+22 = 101. Hinzu kommen die FW 17+84 = 101
der Zahlen 175 und 395 sowie 4*11 = 44. 202+44 ergeben ein zweites Mal 246 als FS von
6 Zahlen.
3. Neben den 4
Komplementärzahlen der Ausgangssituation sind auch noch 571+593 = 1164 Primzahlen. Als FS
kann man daher 8:4 Zahlen gegenüberstellen: 2220*(1164+246) = 1410:2220 =
30*(47:74). Den Einzelziffern der
beiden Umkehrzahlen entsprechen die 11 Elemente der Raute in der DR : 7 Elemente des hexagonalen
Dreiecks und 4 Erweiterungselemente:
|
|
Teilbarkeit
durch 47 tritt noch zweimal auf:
·
Die 6 Primzahlen haben die ZS 2220+1164 = 3384 = 72*47 = FW 59.
·
Jede der beiden Ausgangszahlen und ihre Umkehrung
addiert sich zu 157+751 = 908 = 4*227 = FW 231; 359+953 = 1312
= 32*41 = FW 51; 231+51 = 282 = 6*47.
4. Aus zahlreichen weiteren
Berechnungsmöglichkeiten möchte ich eine einzige herausgreifen: Wenn man
dreistellige Komplementärzahlen und ihre Umkehrungen von der untersten bis zur
obersten Zahl, zuerst die eine, dann die andere, wie oben ausgeführt,
aneinanderreiht, ergänzt sich jedes konzentrische Paar zu 1110. Die FS
der äußeren
zweimal drei Zahlen und der inneren sechs Zahlen liegen nur 8 Zähler auseinander:
1811 ist eine Primzahl. Die Zahlen 18 und 11 sind Numerierungssummen der hexagonalen
Erweiterungen und der Kreisachse, sie repräsentieren das Kreisflächenverhältnis 2:1:
|
|
Die Faktoren von 1819 sind 17*107 = FW 124 = 4*31. Aus 18 und 19
Elementen besteht die Tetraktys. 17 und 107 bedeuten zweimal dasselbe: 10 Tetraktyspunkte und 7 Hexagonpunkte in der Bedeutung von 3:1 Flächeneinheiten.
Die Faktoren 4*31 weisen auf die 4+4 Punkte der DR hin, wenn der Mittelpunkt zweimal gezählt
wird.
Die ZS und FS lassen
sich auf zweifache Weise verrechnen:
·
Die erste
Verrechnung trennt ZS und FS:
|
|
ZS |
FS |
ZS |
FS |
sm |
FW |
|
|
3330 |
1118 |
3330 |
1819 |
10290 |
31 |
|
FW |
50 |
1811 |
50 |
124 |
2035 |
53 |
|
sm |
2035 = 5*11*37 >53 |
|||||
Die
Einzelziffern sind als Entsprechungen von 3:1 Kreisflächeneinheiten
zu 5:3 Radialelementen zu interpretieren.
·
Die zweite
verbindet ZS+FS:
|
|
|
|
sm |
FW |
sm |
|
ZS+FS |
5141 |
5149 |
10290 |
31 |
|
|
FW |
150 |
290 |
440 |
22 |
|
|
sm |
|
|
10730 |
53 |
|
|
FW |
|
|
73 |
53 |
126 |
|
5141 = 53*97; 5149 = 19*271; 126 =
6*21 |
|||||
|
440 = 44*10 = FW 15+7 = 22 |
|||||
Die
Einzelziffern der FW
31 und 22 sind Entsprechungen von 3 hexagonalen Radialelementen zu 1 Flächeneinheit und 2
Erweiterungselementen und 2
Flächeneinheiten.
126 entspricht 6 DR , die sich zu 3 DR-Kreuzen und 3 Oktaedern kombinieren. Die Einzelziffern können als 10 Tetraktyspunkte verstanden werden, 1+26 bedeuten auch Volumen + 26 Oktaederelemente.
Die
Einzelziffern der FW
73 und 53 sind interpretierbar als 3*7 Rahmenelemente der
Tetraktys und 3*5 Achsenelemente des
Hexagons.
Die
Summe der Zahlen von 1-29 beträgt 15*29 = 435. 440 enthält einerseits die
Elemente von 4 Rauten, die einen Oktaeder konstituieren, andererseits weist der
FW 22 auf eine einzelne DR.
Erstellt: Juni
2015, Oktober 2016