Ordnungen der Zahlen 1-20
Die Zahl 365
I.
Drei Kreisachsen und ihre Erweiterung zum Tetraktysstern
II. Konzentrische
Zahlenpaare 1-20
III. Die Nummern 8-10 mit symmetrischen Folgerungen
I.
VIGINTI – zwanzig: gematrische Analyse
Die Zahlen 1-20 in der Doppelraute und in zwei Achsenkreuzen
Summe 365 aus den Zahlen 8 und 9
I. Drei Kreisachsen und
ihre Erweiterung zum Tetraktysstern
1.
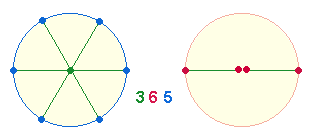
Eine Gerade
durch den Mittelpunkt eines Kreises erzeugt zwei gleiche Maßeinheiten (Linien),
die jeweils durch zwei Punkte begrenzt werden. Punkte,
Linien und Flächen
werden im Folgenden als Elemente bezeichnet. Die zwei Radien eines Kreises
bestehen demnach aus 2*3 = 6 Elementen.
Dabei wird der Mittelpunkt (MP) doppelt
gerechnet. Betrachtet man die beiden Strecken (Radien)
als Durchmesser (DM)
und somit als zusammengehörige Einheit, zählt man den Mittelpunkt
einfach und somit 5 Elemente. 6+5 sind also Grundzahlen einer Kreisachse. Zieht man in gleichem Winkelabstand
zwei weitere Achsen, läßt sich der numerische Ausdruck 3*(6+5) bilden. Dies ist eine
erste Übereinstimmung der physikalischen Wirklichkeit von 365 Tagen des Jahres und des apriorischen Prinzips
eines geometrischen Modells:
|
|
2.
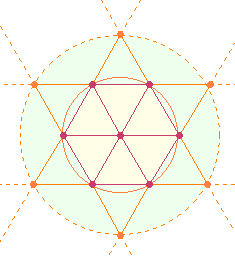
Zieht man
durch die 6 Kreislinienpunkte ebensoviele
Gerade, entsteht ein Sechseckstern mit zwei gegenläufigen Dreiecken aus je 1+2+3+4 Punkten, die man Tetraktys
(griech. Vierheit) nennt:
|
|
In zwei Tetraktys zählt man also 20 Punkte. Zu den 7 Punkten des Hexagons kommen
noch jeweils 3
Eckpunkte hinzu.
II. Konzentrische
Zahlenpaare
1.
Um die Summe
der Zahlen (ZS) von 1-20
zu berechnen, addiert man sie konzentrisch: 1+20, 2+19
usw. 10 solcher Additionen ergeben somit 210. Im
lateinischen Alphabet zeigt sich diese konzentrische Betrachtungsweise darin,
daß sich der 1. Buchstabe A
und der 20. Buchstabe V zum 21.
Buchstaben X
zusammensetzt.
Bei einer zweiten Zählung addiert man die
Primzahlfaktoren einer Zahl: 6 = 2*3 hat z.B. den Faktorenwert
(FW) 5:
|
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
210 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
155 |
Die FS 155 und
die ZS 210 ergeben die reale Zahl 365,
die zuvor aus dem Verhältnis 3*(6+5) der
drei Hexagonachsen zusammengesetzt war. Das FS:ZS-Verhältnis ist 155:210 = 5*(31:42) = 5*73. Die Verhältniszahlen 31 und 42 bestehen
aus den Tetraktyszahlen 1-4, den
Einzelziffern der Summe 73 entspricht die Entwicklung der Tetraktys
aus den 7
Punkten des Hexagons.
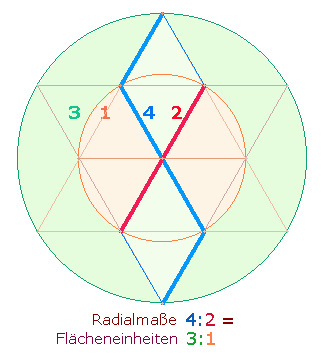
Die Einzelziffern der beiden Zahlen 31 und 42 haben
einen wesentlichen Bezug im Flächenverhältnis der beiden konzentrischen
Tetraktyskreise und den Radialmaßen der Durchmesserlinien:
|
|
Das Flächenverhältnis
3:1 = (2+1):1 bezeichnet
abbildhaft die Existenz eines Gottes in drei Personen, worauf auch die drei
Achsen des Hexagons hinweisen.
2.
Das FS:ZS-Verhältnis 31:42 wiederholt
sich konzentrisch in je zwei äußeren
und zwei inneren
Zahlenpaaren:
|
Bu. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
V |
|
ZW |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
|
|
3 |
12 |
18 |
31 |
30 |
33 |
28 |
|||||||||||||
Die beiden konzentrischen Einheiten von 8 Zahlen schließen zwei Einheiten von jeweils 2*3 Zahlen ein. Die Summe von jeweils drei
aufeinander folgenden FW ist durch 3 teilbar:
Das Verhältnis der 6 äußeren zu den 6 inneren FS
ist 45:48 = 3*(15:16).
Von außen nach innen ergeben demnach proportional 4:12:4
Zahlen das FS-Verhältnis 31*(1:3:1).
3.
Ein gleiches FS:ZS-Verhältnis
ergeben auch die mittleren beiden Zahlen jeder Zehnereinheit bei konzentrischer
Zuordnung:
|
ZW |
5 |
6 |
|
15 |
16 |
|
FW |
5 |
5 |
|
8 |
8 |
|
13:21 |
|||||
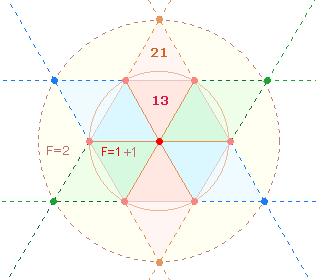
Jede konzentrische Paarung ergibt dasselbe FS:ZS-Verhältnis 13:21. Somit zeigt sich zweimal eine gleiche ZS+FS: 13:21 + 31:42 = 44:63 = 107.
Die Zahl 107, in 10+7
aufgeteilt, gibt das Flächenverhältnis 3:1
wieder. Denn die 10 Punkte der Tetraktys
erstrecken sich über beide konzentrische Kreise mit 3 Flächeneinheiten, den 7
Punkten des Hexagons entspricht 1
Flächeneinheit.
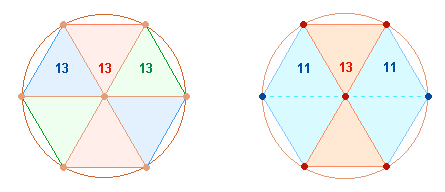
Die Summen 13
und 21 sind auf die Elemente der Doppelraute (DR) beziehbar: 13
Elemente gehören dem hexagonalen Bereich an, aus 21
besteht die gesamte DR, das wiedergegebene
Flächenverhältnis ist 1:3:
|
|
4.
Von besonderer
Bedeutung ist die konzentrische Fortsetzung der zwei äußeren Zahlen:
|
Bu. |
A |
B |
C |
D |
|
R |
S |
T |
V |
|
ZW |
1 |
2 |
3 |
4 |
|
17 |
18 |
19 |
20 |
|
FW |
1 |
2 |
3 |
4 |
|
17 |
8 |
19 |
9 |
|
42:63 = 21*(2:3) |
|||||||||
|
63:84 = 21*(3:4) |
|||||||||
Die Verhältniszahlen 2:3 und 3:4
lassen sich auf die 5+7 Elemente der Kreisachse
und einer Tetraktysseite beziehen. Ihre eigentliche Bedeutung
liegt in den Differenzverhältnissen zwischen FS
und ZS: 2:1 und 3:1, worin sich die 3 und 4 konzentrischen Zahlenpaare widerspiegeln. Es
handelt sich um die grundlegenden trinitarischen Zahlen,
die z.B. an der Tetraktysseite zu erkennen sind:
|
|
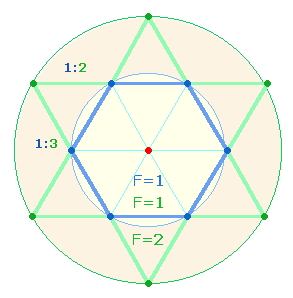
Die Erweiterung des Hexagons zum Sechseckstern fügt
jeder Segmentlinie zwei weitere Maßeinheiten hinzu. Dieser
Erweiterungsvorgang stellt sich als Verhältnis 1:2
dar. Insofern aber Hexagon und Tetraktys zwei eigenständige geometrische
Figuren sind, wird jede einzelne Segmentlinie überlagert von drei
Maßeinheiten, wodurch sich ein Verhältnis 1:3 ergibt.
5.
Die drei
äußeren Zahlenpaare begründen das System
VESTA:
|
Bu. |
A |
B |
C |
|
S |
T |
V |
sm |
|
ZW |
1 |
2 |
3 |
|
18 |
19 |
20 |
63 |
|
FW |
1 |
2 |
3 |
|
8 |
19 |
9 |
42 |
|
42:63 = 21*(2:3) |
||||||||
Die ZS+FS der beiden äußeren Paare bildet zu der des
inneren Paares das 63:42 = 21*(3:2).
Das entsprechende FS-Verhältnis von 4:2 Zahlen hat den Umkehrwert 1:2.
Aus der Addition 2+3
geht der ZW für das E, den 5.
Buchstaben, hervor:
|
Bu. |
A |
E |
S |
T |
V |
|
|
ZW |
1 |
2 |
3 |
18 |
19 |
20 |
Die Kontraktion der Zahlen 2
und 3 hat die Auswirkung, daß sich die
übrigen 4 Zahlen aufteilen in 1:3 in den ZW 19+FW 19 = 38 und die
ZS 39 + FS 18
= 57 und so zum FS:ZS-Verhältnis 21*(2:3) das ZS+FS-Verhältnis
19*(2:3) hinzukommt.
Durch Buchstabenumstellung erhält man den religionsgeschichtlichen
Begriff VESTA. Beide Begriffe sind als A EST V und V
EST A zu verstehen,
also eine Tetraktys ist gleich der zweiten. Der erste Begriff der Gleichung ist
der zu definierende, der zweite der übergeordnete oder bekanntere. Das A
ist der erste Buchstabe, der den letzten vorgibt.
Wie ist die Vertauschung des A und des V zu erklären? Als eine erste
Begründung wird man die natürliche Wahrnehmung geographischer
Oberflächengestalt anführen, daß nämlich die Spitze oben und die Basis unten
ist. Eine tiefere Begründung ist theologischer Natur. Die göttliche Weisheit
bietet dem Menschen keine vollkommene Lösung an, sondern den Spielraum eigenen
Mitwirkens als eine dialogische und kommunikative Beziehung zwischen Gott und
Mensch.
6.
Das VESTA-Modell 42:63 = 105 ist noch
in drei weiteren konzentrischen Zahlenpaaren verwirklicht:
|
ZW |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
|
|
6 |
|
17 |
|
|
|
|
|
|
25 |
|
36 |
||||||||
Die ZS+FS von 6
konzentrischen Zahlenpaaren umfassen somit die Gesamt-ZS 210, die der übrigen 4 die Gesamt-FS 155.
Nimmt man das dazwischen liegende Zahlenpaar 4+17 mit identischer ZS und FS hinzu,
ist das FS:ZS-Verhältnis
105:147 = 21*(5:7) = 21*12 = 252.
Die FS der übrigen 6
FW ist 50.
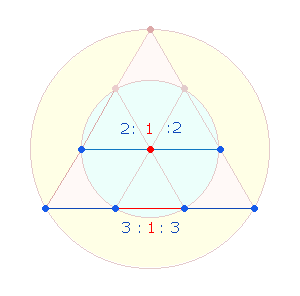
Die ZS der ersten 7
Zahlenpaare haben die symmetrische Struktur 3:1:3, die FS
2:1:2.
Beide Strukturen sind in der Doppelraute und parallel, aber weniger relevant,
in den DM-Elementen der Kreisachse sowie in den Elementen einer Tetraktysseite
erkennbar:
|
|
|
7.
Man kann die FW konzentrisch von 1-10
numerieren (20=1,
19=2 usw.),
gleiche Nummern (N) addieren und Kombinationen
von FS ermitteln, die durch 21 teilbar sind:
|
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
FW |
10 |
21 |
11 |
21 |
13 |
13 |
16 |
19 |
13 |
18 |
8.
Drei Paarungen von FS
ergeben jeweils 29,
zwei Paarungen 34:
|
N |
1 |
8 |
3 |
10 |
5 |
7 |
2 |
9 |
4 |
6 |
|
FW |
10 |
19 |
11 |
18 |
13 |
16 |
21 |
13 |
21 |
13 |
|
|
87 |
68 |
||||||||
Die Zahl 29 ist
beziehbar auf die Durchmessernumerierung der 9 Elemente der beiden Tetraktyskreise, wobei die
Numerierungssumme 11 dem hexagonalen und die
Zahl 18 dem Erweiterungsbereich angehört (2.
Paar). In der Aufteilung 13 Punkte und 16 Linien wird man an die Rahmenelemente des DR-Kreuzes denken (3. Paar). Über das Verhältnis 21:13 wurde bereits weiter oben
gesprochen.
Die Addition 29+34 = 63
ergibt zweimal zusammen mit den ZS das Verhältnis 63:84 = 21*(3:4) = 3*7*7 = 3*49 = 3*(7+17+25) = 147,
mit 2 multipliziert =
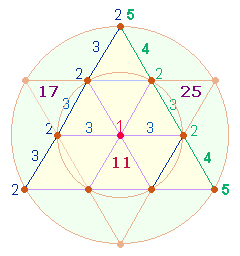
294. Aus 3
Linien und 4
Punkten besteht eine Tetraktysseite, für die sich durch einen zweifachen
Numerierungsmodus die Summen 17 und 25 ergeben:
|
|
Durch Dreifachzählung erhält also jede der 6 Tetraktysseiten die Summe 49.
III. Die Nummern
8-10 mit symmetrischen Folgerungen
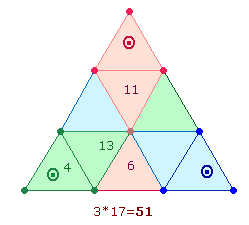
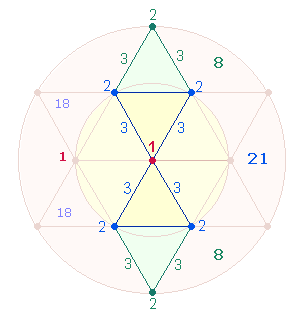
1.
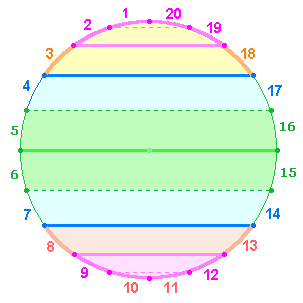
Die
verschiedenen Ordnungen der Zahlen 1-20 können in Kreisform etwa folgendermaßen
dargestellt werden:
|
|
Zwei äußere (1+20, 2+19) und innere
(10+11, 9+12) Zahlenpaare bilden zunächst
eine symmetrische Gleichheit des Verhältnisses 31:42. Die Fortsetzung der äußeren
zwei Zahlenpaare ergibt jeweils Teilbarkeit der FS
und der ZS durch 21
bis einschließlich 7-14, wobei die Nummern 1-3 und 5-7
zusammengehörige Einheiten mit dem Verhältnis 2:3 bilden.
Die Zahlenpaare 5-16
und 6-15 bilden die symmetrische Mitte des
Kreises. Aus Gründen der Symmetrie und da die FS
der beiden Zahlenpaare jeweils 13 beträgt,
wird man nicht nur 7-14, sondern auch 4-17 dieser Symmetriemitte zurechnen. Das FS:ZS-Verhältnis
dieser 4 Zahlenpaare ist 21*(3:4) = 147,
ebenso wie das der ersten 4 Zahlenpaare.
Es ist bedeutsam festzuhalten, daß das Nummernpaar 4 beiden Zahlengruppen angehört.
2.
Während sich
die FS der zwei äußeren
Zahlenpaare zum Verhältnismuster 21*(2:1:2)
ausweiten, weisen die beiden inneren eine
andere Fortsetzung und Beziehung zu den eben festgestellten zwei Vierergruppen auf. Das dritte Zahlenpaar 8+13 erweitert die FS
der beiden ersten von 31 auf 50:
|
8 |
9 |
10 |
|
|
19 |
13 |
18 |
50 |
Analog zu den ersten beiden Gruppen geht es darum,
die beiden Verhältnisse 2:3 und 3:4, also die FS 42
und 63 zu gewinnen. Ersteres Verhältnis ist
zweimal mit den Nummern 1 und 3 möglich und damit auch das Verhältnis 2:3:
|
3 |
9 |
10 |
1 |
8 |
9 |
|
11 |
13 |
18 |
10 |
19 |
13 |
Das FS-Verhältnis
ist 21:63, das ZS-Verhältnis 42:84.
3.
Mit der zweiten Vierergruppe weisen die Nummern 8-10 eine besondere Beziehung auf:
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
21 |
13 |
13 |
16 |
19 |
13 |
18 |
Die FS des
ersten und dritten Zahlenpaares 19+18
ergeben ebenso 37
wie die FS 21+16 des Mittelteiles. Als
Außenglieder ihrer Zahlengruppe umschließen diese FS
jeweils die FS 13 im Verhältnis 1:2.
In chiastischer Addition betragen die zwei
Außenglieder 39, die zwei
Innenglieder 35. Die beiden
Summen sind auf die Elemente von jeweils drei Figuren des Hexagon beziehbar:
|
|
Die Zusammengehörigkeit der beiden chiastischen
Paaren zeigt sich in ihren FW:
|
FS |
18 |
21 |
19 |
16 |
74 |
|
FW |
8 |
10 |
19 |
8 |
45 |
|
sm |
18 |
27 |
119 |
||
|
18:27 = 9*(2:3) |
|||||
4.
Zur ZS 63 bedürfen die Nummern 8-10 einer ZS 13 der zweiten Vierergruppe. Es zeigen sich somit zwei
parallele Bildungen der zweiten und der dritten Gruppe:
|
4 |
5 |
6 |
7 |
5/6 |
8 |
9 |
10 |
|
21 |
13 |
13 |
16 |
13 |
19 |
13 |
18 |
Das FS-Verhältnis
ist 13:50, das ZS-Verhältnis 21:63.
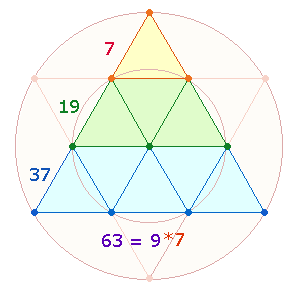
Zweimal besteht die Summe 63
aus 26+37. Die beiden Summen sind Elementen
der addierten Dreiecksebenen 1+2+3 der
Tetraktys zuzuordnen:
|
|
Die zwei parallelen ZS
63 lassen klar den Bezug der Zahlen 1-20
zu den beiden Tetraktys erkennen.
Durch die Ergänzungen der Nummern 8-10 zu den Verhältnissen 2:3 und 3:4 wurden diese selbst zu einer Vierergruppe. Die ZS+FS einer Vierergruppe der beiden Verhältnisse
beträgt, wie oben ermittelt 252. Da ein weiteres 2:3 Verhältnis hinzukam, beträgt die Gesamt-ZS+FS 3*252+105 = 861 = 21*(36+5)
= 41*21. Die
Entlehnungen der dritten Vierergruppe und
deren eigenen Werten führen zu folgenden ZS+FS: 315+(286+260)
= 15*21+26*(11+10) = 41*21.
5.
Nachdem nun
drei Vierergruppen feststehen, ist noch eine letzte analoge Folgerung zu
ziehen: Wenn die Nummer 4 zur ersten und zur
zweiten Gruppe gehört, also doppelt zu zählen ist, sollte dies auch für die
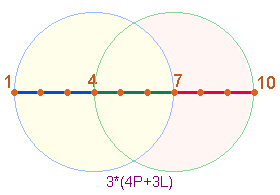
Nummer 7 gelten. Die drei Vierergruppen kann
man auf einer Punktestrecke von 1-10 veranschaulichen:
|
|
Um die Punkte 4
und 7 kann man jeweils einen Kreis schlagen
mit dem Radius von 3 Maßeinheiten. Ein Kreis
umfaßt damit 7 Punkte und 6 Linien = 13
Elemente, eine Vierereinheit 4 Punkte und 3 Linien wie die drei Seiten der Tetraktys, die man
durch Hochklappen der zwei Seitenteile bilden kann.
Fügt man die ZS+FS 42 des 4.
Nummernpaares zu 365 = 5*73, erhält man mit 407
= 11*37 den Umkehrfaktor 37. Die ZS+FS des 7. Nummernpaares beträgt 21+16 = 37, fügt also einen 12.
Teil 37 hinzu. 12*37
aber ist 444 und bestätigt somit die drei Vierergruppen.
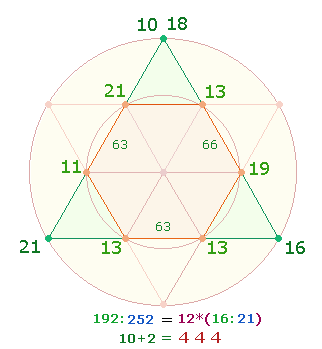
Die 10
Nummernpaare lassen sich den Punkten des Tetraktysrahmens zuordnen:
|
|
Das Verhältnis 192:252 ergibt sich aus der Verdoppelung der ZS+FS des 4. und 7. Zahlenpaares:
|
|
1-10 |
4 |
7 |
|
|
ZS |
210 |
21 |
21 |
252 |
|
FS |
155 |
21 |
16 |
192 |
|
|
365 |
42 |
37 |
444 |
Die 12 ZS+FS lassen sich
aufteilen in 6 hexagonale und 6 Eckpunktwerte. Es bestehen folgende Beziehungen
und Verhältnisse:
|
|
hex |
Eckp |
|
|
ZS |
126 |
126 |
252 |
|
FS |
90 |
102 |
192 |
|
|
216 |
228 |
444 |
|
90:126 = 18*(5:7) |
|||
|
102:126 = 6*(17:21) |
|||
|
90:102 =
6*(15:17) |
|||
Beachtenswert ist das Verhältnis 17:21, das
identisch ist mit der ZS+FS der maskulinen Endung -US.
Es hat darin trinitarische Bedeutung, daß die Fischfigur aus drei Dreiecken aus 17
Elementen besteht, jedoch aus 21, wenn man für
jedes Dreieck 7 Elemente zählt. In zwei
Tetraktys kommt diese Figur 6-mal vor:
|
|
6.
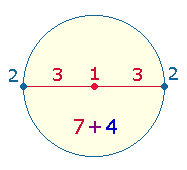
Für das
Verhältnis 16:21
erscheint folgende Erklärung denkbar: Die Numerierung der 5 Kreisachsenelemente von 1-3
ergibt die Numerierungssumme 11, die in 7+4
aufgeteilt werden kann:
|
|
Die Summen 7 und
4 weisen u.a. auf die 7
Punkte und 4 Dreiecksflächen der Doppelraute
voraus. Die Parallele gilt auch, wenn ein zweiter Mittelpunkt für den zweiten
Radius bzw. die zweite Raute gesetzt wird. Dem entspricht zunächst die Addition
des 4.
Nummernwertes 42 zu 365
und dem Verhältnis 11*(16:21), das durch 16+21 des 7. Nummernwertes um einen Zähler auf 12 ansteigt.
Numeriert man in der gezeigten Weise die 15 Rahmenelemente der Doppelraute, ergibt sich für
das hexagonale Achsenkreuz 11+10 = 21 und
für die 6 Erweiterungselemente 2*8 = 16:
|
|
Auch ein
unnumeriertes DR-Kreuz ohne Querlinien ist denkbar.
Die FS 16, die ja eigentlich Teil der ZS ist, wird den Erweiterungselementen zugeordnet.
Die Einzelziffern weisen außerdem auf die 1+6
Punkte des Hexagons und 2+1 Eckpunkte der Tetraktys
hin.
7.
Durch 111 teilbare Summen setzen sich gewöhnlich aus
dreistelligen Umkehrzahlen zusammen. Die kleinste dreistellige Summe aus
Umkehrzahlen ist eben 444. Es handelt sich um
die Zahlen 112+121+211 mit den FW 15+22 = 37+211
= 248 = 8*31 = FW 37. Die Einzelziffern der drei
Umkehrzahlen bezeichnen das Flächenverhältnis 1:3 der beiden Tetraktyskreise, FS/FW 37 weisen
auf die 10 Punkte und 37 Elemente der Tetraktys hin.
Erstellt:
Mai 2011
Letzte Änderung: März
2013